从印度乘法口诀想到的数学教育问题

鄢青云+张弦

摘 要 从印度乘法口诀的教育中得到启发，再结合本人从教三十多年的经历，觉得简化数学教育，对于非数学专业的学生来说，是当务之急，他们没必要花大量的时间用在“为什么”上，而是需要懂得“怎么用”“如何用”。

关键词 创新 简易 直观 易懂

中图分类号：G623.5 文献标识码：A

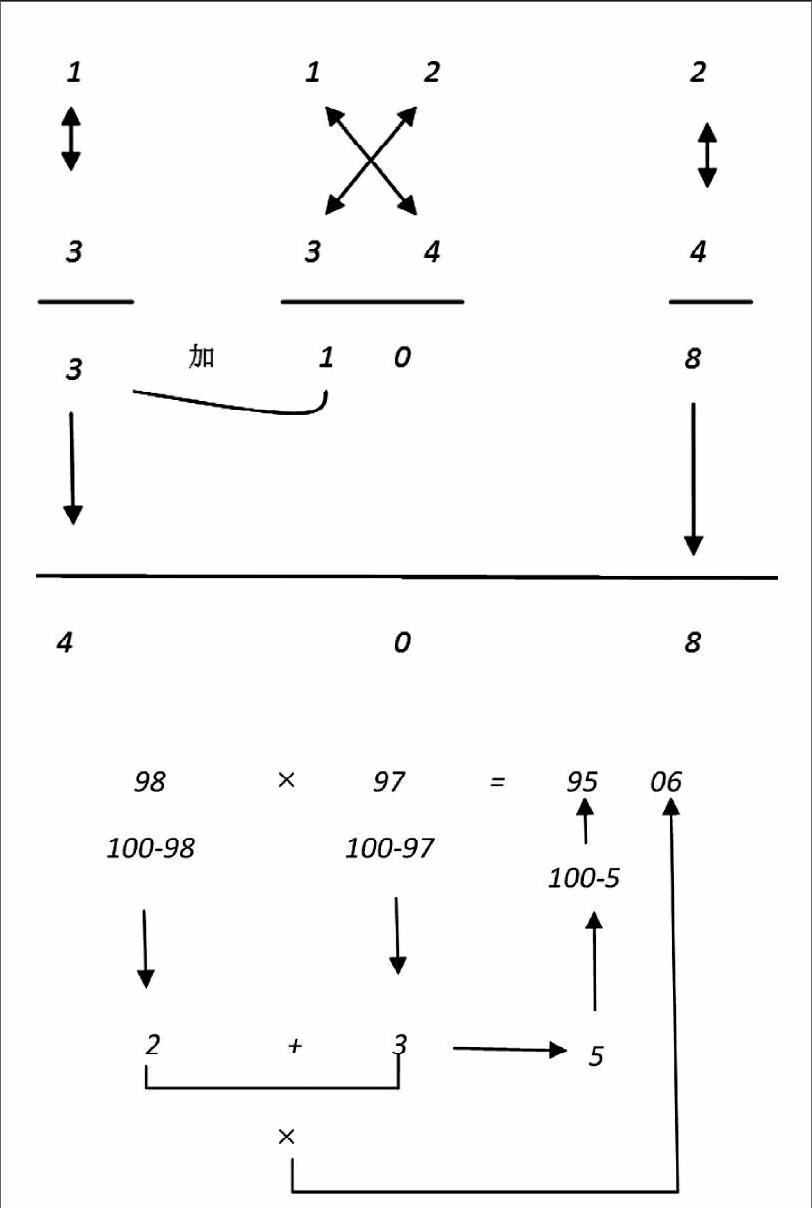
一个偶然，看到关于印度人教乘法的方法，大概的意思是：1919以内的乘法问题，可以分解为四步走。举个例子，问：1716=？，为了算出它的结果，第一步：17+6=23；第二步：2310=230；第三步：7+6=13；第四步：230+13=243，这就是最终结果。表面上，一个乘法问题分解为四步做变复杂了，实际上，它是把高级运算转化为低级运算，而人类擅长的是低级运算，从而使人们可以进行口算。这种方法的使用，不仅可以口算1919以内的乘法，而且可以推广。比如：1234=？

从上面的图示读者不难看出，1234=408，这样的运算很神奇。再比如：9897=？

显然，9897=9506，这两个乘法问题都渗透了加减运算，为什么可以将乘法转化为加、减法来做？它是有数学上的理论依据的，它的依据就是巧妙地利用公式（a+b）（c+d）=ac+ad+bc+bd，尽可能地将乘法问题转化为加、减法，从而达到口算的目的。

其实，数学上有许多趣题，不用传统的数学方法，而是将它回归到生活中，用一种解说的方式找到正确答案。比如：“鸡兔同笼”问题，说的是在一个笼子里住着100只兔子和鸡，告诉你共有320条腿，问兔子有多少只？鸡有多少只？这个数学问题，用方程来解，可以解出结果，但是有点繁琐。有种方法直接、简单，而且还很生活。其解题思路是从上往下思索，100个头下都是4条腿的一定是兔子，这样应该有400条腿，而事实上，只有320条腿，多算了400-320=80条腿，这多出来的80条腿，是把鸡当成兔子来算，这时我们就要卸掉2条腿，每卸一次，就把兔子转化为鸡，卸几次，就有几只鸡，于是，鸡有802=40只，兔子有100-40=60只。

上述解说，读者可能认为有道理，也算是简易解法了。没有最好，只有更好，同样的问题，不同的思路，决定着解题的难易程度。还是上面的“鸡兔同笼”问题，我们来个从下往上思索，看效果如何？想像一下，你面前站着100只鸡和兔子，你手上拿着一把神奇的刀，砍下去对动物没有生命威胁，这时，你对每只动物砍掉两条腿，鸡全部趴下了，而兔子依然还可以站着（4条腿的兔子拿掉2条腿，还有2条腿撑着），于是，兔子有：（320-2100）2=60只，鸡有100-60=40只。

印度人在进行小学生乘法口诀的教育上，应用的是初中才能学到的乘法运算法则，而他高明的地方就在于，抛弃理论，并将理论直接转化为方法。而我国小学生的乘法口诀定格在九九乘法表上，竖式、进位求乘法，虽然一本万利，但严重阻碍了学生的计算能力，这种教育上的差距不是一般的大呀。

再来看看极限概念的定义，纯数学理论习惯于用“€%^-€%]”语言来描述，但对于大部分非数学专业的学生来说，他们不需要知道“为什么？”，他们需要的是如何方便快捷地“怎么用？”。印度人教乘法的方法值得我们借鉴。实际上，数学上的许多知识，我们是可以做些转换的。

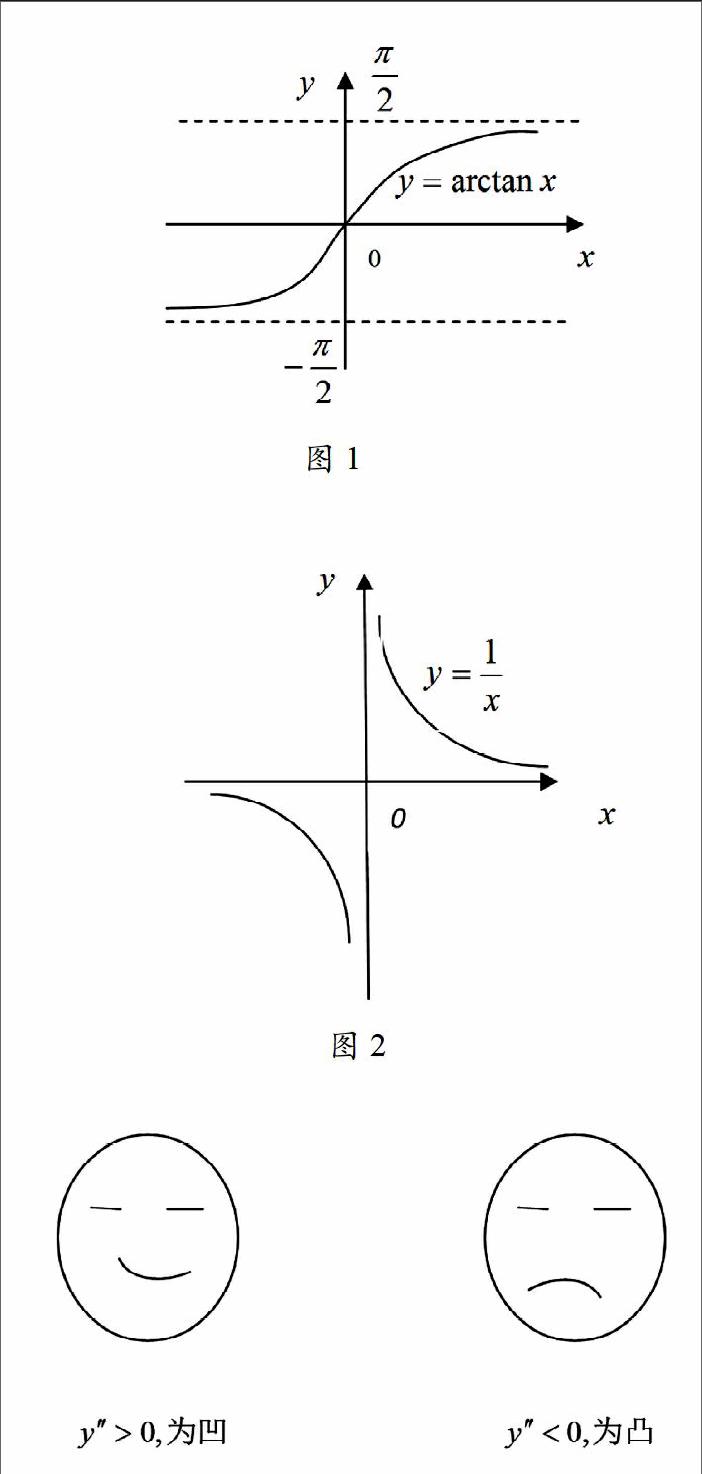
“极限”的概念”语言晦涩难懂，对某个函数来说，如果当自变量变化的时候，因变量呈现“无限逼近某一个常数”的特征，那么我们就说该函数存在极限。这种形象化的语言，学生更容易接受，如果再配上图形，效果更佳。

显然，由图1知： arctanx=，arctanx=，arctanx不存在；而圖2显示，当自变量x→∞时，函数→0，于是有=0，这样借助图形理解极限概念，简单直观得多。当然，计算极限值，我们有一整套的理论体系，总结起来，大体有五条路可行：第一条路，f（x）=f（x0），这条路有两个缺陷，一是x必须趋近于某个实数x0；二是x0必须是f（x）定义域里的点，假如不是，进入第二条路：x0代入到f（x）中，造成分母为0，这时就看分子，分子的结果不外乎两种情形0或非0，为了叙述方便起见，我把它记着型或（A≠0）型，对于型，可用洛必达法则、无穷小的等价代换等方法，而（A≠0）型的结果只有一个，那就是无穷大。第三条路是专门针对x→∞的情形，当x→∞时前两条路都行不通。这时使用洛必达法则是很有效的，或者尽可能制造（€%Z>0），再配合极限的四则运算法则来完成，效果奇佳。第四条路使用公式：（1+）x=e或（1+x）=e，该公式的特点是底与指数都是关于x的表达式。第五条路依据“有界函数与无穷小的积是无穷小”，此法不需要解题过程直接写出结果，如：x2cos=0，计算极限问题，有了这五条路做为行动方向，纷繁复杂的极限问题变得明朗了许多。我想，这就是教育工作者常应思索的问题。

数学有许多定理，死记硬背不可取，理解的基础上记忆，效果好。如果再渗入方式方法的应用，那将是根深蒂固的。在刻画曲线凹凸问题时，有个判断定理：设函数y=f（x）在[a，b]上连续，在（a，b）内有一阶和二阶导数，则若在（a，b）内y''>0，则曲线y=f（x）在[a，b]上的图形是凹的；若在（a，b）内y''<0，则曲线y=f（x）在[a，b]上的图形是凸的。文字很长，看下面两图的嘴型，便一目了然。

两张脸谱，就能表达一个数学定理的核心思想，我就在想，我们可以进行大胆创新，将几千年的数学文化变得直观、简易、好懂。与时俱进，共同创造高效、有趣的生活。让数学更接地气，让人们不再觉得数学高不可攀。