机器学习中K—means聚类算法的分析和应用

王子桥

摘 要：本文采用机器学习中的聚类算法对高水平足球联赛五十名顶尖球员的进攻数据进行无监督聚类学习和分析，并以进球数、射正数和助攻数为评价指标，将球员分成三个类别。本文首先分析了K-means聚类算法的流程和特点，进而应用于对足球运动员比赛数据的聚类运算。对聚类后的分类结果进行分析和比较，从而找出球员的优势劣势。其结果不仅对球员个人发展有极大的指导作用，也对中国足球取长补短、提升自身能力有重要意义。

关键词：K-means算法；聚类；机器学习

中图分类号：TP18 文献标识码：A 文章编号：1671-2064（2017）04-0030-02

计算机是迄今为止最为高效的信息处理工具，特别是近年来随着互联网的发展，应用计算机辅助工作和学习已经成为常态。但普通计算机缺乏自主学习的能力，只是被动地执行人为设定好的程序。因此人们开始寻找一种能以与人类智能学习相似的方式进行数据处理的方法，于是人工智能应运而生。

从1997年深蓝在国际象棋中战胜卡帕罗耶夫，到2016年AlphaGo在围棋中击败李世石，不难看出，人工智能的发展潜力十分巨大。然而，目前的人工智能仍处于十分初级的弱人工智能阶段，想要进一步发展人工智能就必须探索新的更有效的方法。

近年来，人工智能领域中的重要方向——机器学习，得到了越来越多的重视，顾名思义，机器学习是通过经验自动改进计算机算法的研究，[1]也就是说，机器学习能用数据或以往的经验优化计算机程序的性能标准，在不断进行自我学习的过程中，对机器自身程序算法进行优化。在机器学习中，聚类是一种极其重要的算法。聚类源于包括数学、计算机科学、经济学、生物学等的许多领域，其工作原理是通过研究各个样本之间的相似度，利用数学方法对样本进行分类。[2]这其中，K-means算法是最为经典的聚类算法之一。K-means算法是聚类分析中一种基于划分的算法，属于无监督的学习，该算法是聚类分析中一种十分经典且非常高效的方法，具有高效率和相对可伸缩的优点，在处理大数据集时简单快速，十分方便。[3]

1 K-means算法

作为一种无监督的聚类算法，K-means算法在解决多个样本数据进行分类的问题时十分有效，给定一组样本{}，K-means算法将会把样本聚成k个簇，具体步骤如下：

（1）根据给定的k值随机选取k个质心{}。

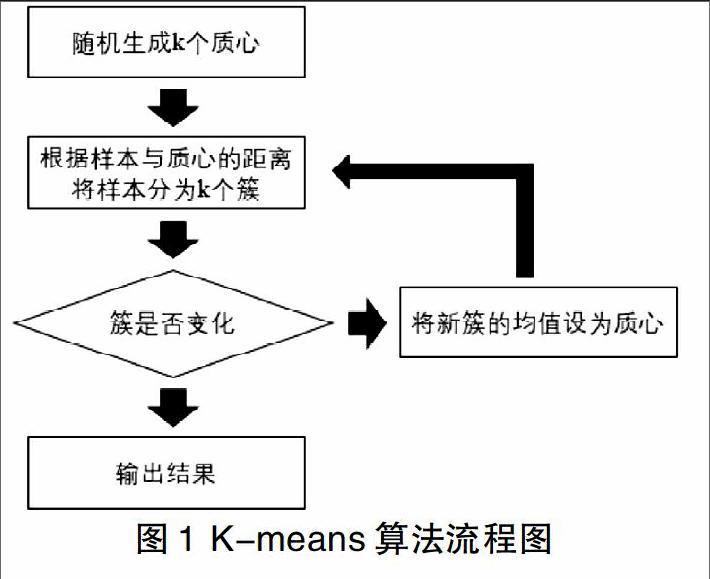
（2）重复迭代两步直到质心不变或变化很小：1）计算每一个样本i应属于的类别=argmin，2）对每一个类别j，重新计算它的质心，其中k是已知的聚类数，是样本i与k个类别中最近的一类，质心位置是初始随机选定的。其算法流程图如图1所示。

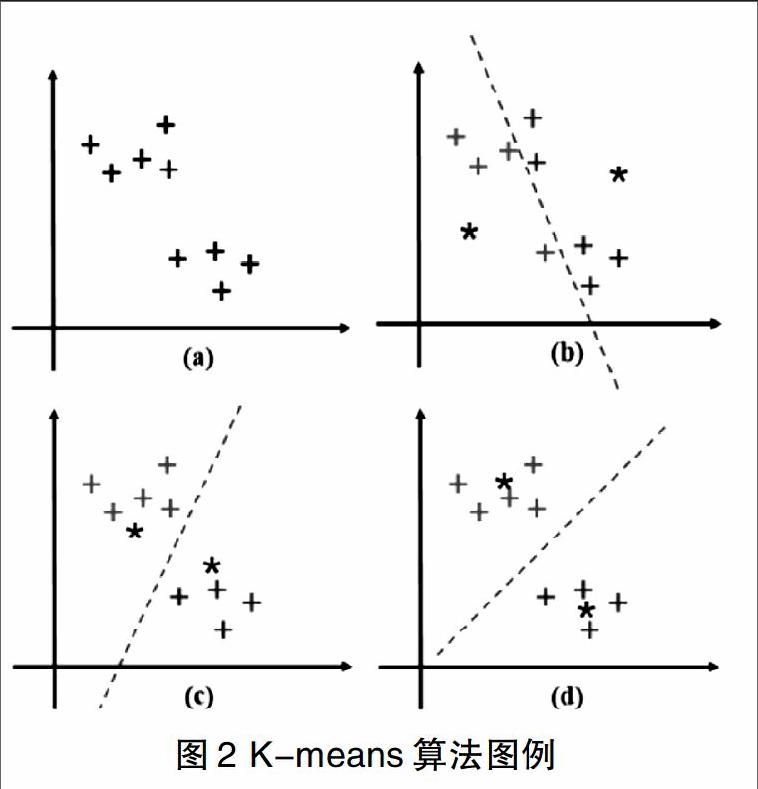
下面用算法图例来展示K-means算法的具体运算流程，如图2所示。

如上图所示，数据的初始分布如图（a）所示，数据点用二维平面的加号 ”+”表示，共9个数据点。在图（b）中，用星号“*”表示K-means算法的初始聚类中心。根据上述算法流程，K-means通过计算初始聚类中心到数据点的欧氏距离对样本点进行第一次分类，用红色与绿色表明第一次的分类结果，结果如图（b）所示。在第一次分类后，对每一类的全部样本点重新计算质心，再次计算样本与每个质心的距离进行下一次分类，结果如图（c）。重复该过程直到聚类质心的位置不变或质心变化很小达到稳定状态，结果如图（d），最终得到了样本的2分类结果。

由以上介绍，我们可以看出K-means算法操作简便，分类效率高。在速度上有很明显的优势，特别是在处理大量复杂样本时，K-means能利用比较各个样本相似度特性的方法就使问题得到简化，从而达到快速分类的目的。它的另一优点是时间复杂度较低，其时间复杂度可以表示为O（nkt）。n是数据集中对象的数量，k是类别数，t是迭代次数。也就是说，其时间复杂度是近于线性的，相对于其他的聚类算法复杂度较低。

然而K-means算法只能達到局部最优，因此在其k值的选择和初始质心的选取上较难控制，不同取值会导致较大的差异.且K-means对数据源要求较高，只适用于球状分布的聚类特性数据，不能处理非球状分布或差别很大的样本集，这是该算法一个很大的局限性。另外，因为迭代次数无法确定，K-means算法的算法不够稳定，在某些特殊的数据集上可能导致其复杂度急剧增加，导致算法的运行效率较低。

2 球员数据应用

足球运动员在训练或比赛中会有许多个人表现的数据，比如进球数、助攻数等等。对球员数据的合理分析有助于指导球员的训练和提升技术水平。本文收集了欧洲范围内五大高水平联赛50名顶尖球员（排名榜前十名）的运动数据。由于所列球员都为进攻性球员，故采取进球数、助攻数、射门成功率为评价指标，其中射门成功率为 （进球数/射门数）*100%。由于各个数据的变化范围不统一，因此首先对数据进行归一化处理，再读入K-means程序进行聚类分析。

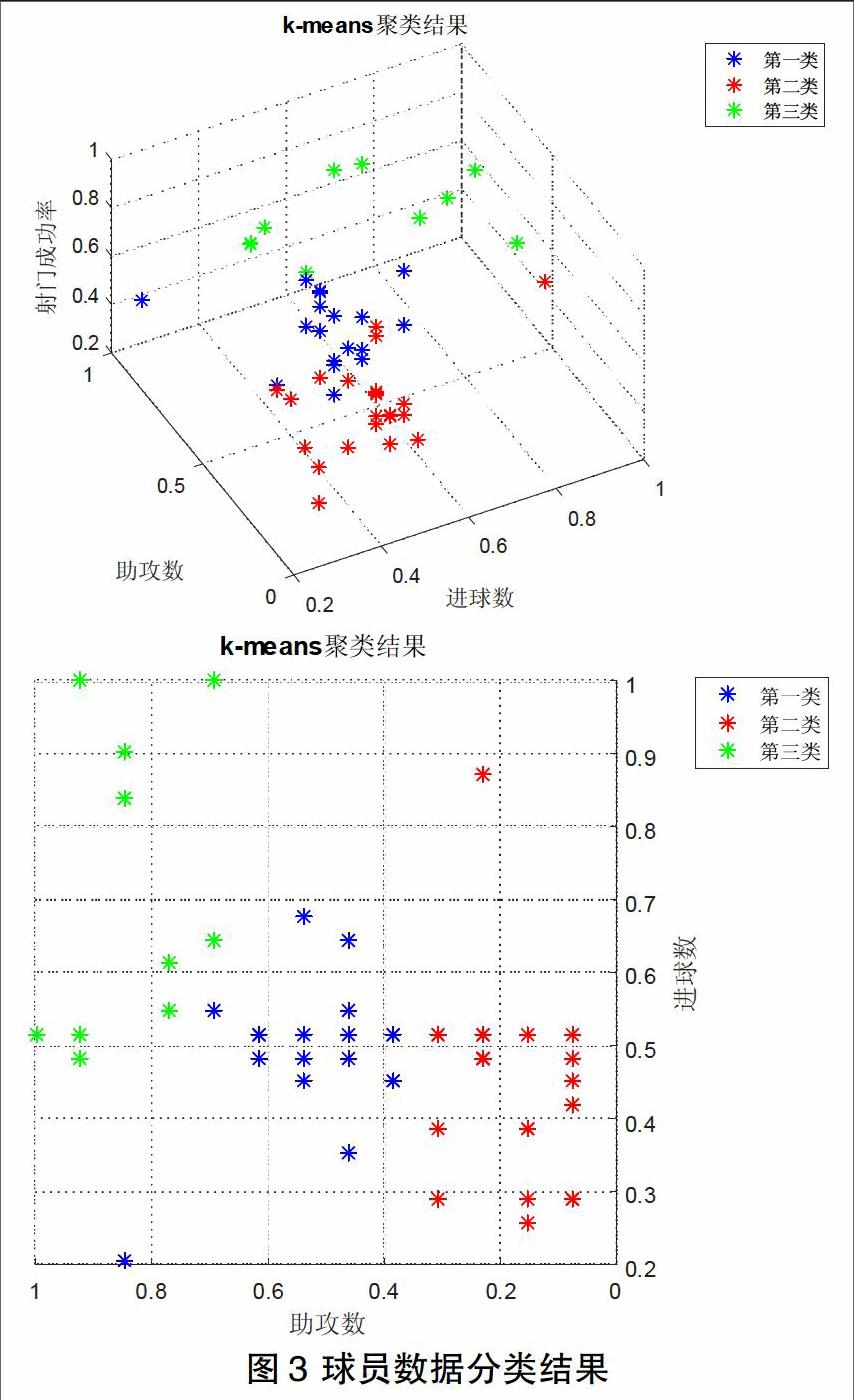
在经过归一化处理之后，将50组数据读入K-means算法程序，并通过进球数、助攻数和射门成功率三维坐标进行显示，其分类结果如图3所示。

由该分类结果我们可以看出，越靠近坐标为（1，1，1）的点说明球员的数据越突出。在本结果中，绿色类为数据较优秀的球员，蓝色类为数据一般的球员，而红色类为数据较差的球员。在助攻数和射门成功率上，绿色类都要明显优于其他两组，而在进球数上，三个类别没有体现出明显的分类差异。特别是，在助攻数这一评价标准中，三类的区分度尤其明显，这也就意味着，助攻数和射门成功率是衡量一个优秀球员最为关键的因素，而不仅仅是考量进球数。这一点与人们一般认可进球数的常识相悖。因此要想成为一名优秀的足球运动员，除了在保证进球数的基础上，提升助攻和射门成功率也是十分重要的方面。

但是，在本方法中也存在一定不足。比如数据的采集，总共选取了50名球员的运动数据，而且主要取自于顶尖排名，但并不一定能够代表所有足球运动员的实际水平，具有一定的局限性。另一方面，本方法所分析的助攻数、进球数和射门成功率这三项指标并不能完全代表一个球员的场上表现，只是选取了三个可量化的评价指标，为了得到更为全面的评价结论，还需要更加全方位的分析和总结。

3 结语

本文分析了机器学习中无监督聚类算法K-means的详细流程和典型应用。对该算法的实现过程、算法流程进行了仔细的分析和讨论。并将该算法应用在对顶尖足球运动员运动数据的聚类分析上，以进球数、射正数和助攻数为评价指标，将球员分成三个类别。并对聚类后的分类结果进行分析和比较，发现助攻数是较进球数影响更大的因素，从而找出分辨球员的优劣的新标准。该结果对足球运动员个人能力的提升上意义重大，更对中国足球未来的发展有一定指导作用。

参考文献

[1]曾华军，张银奎，等译.《机器学习》Tom M Mitchell[M].机械工业出版社，2003.

[2]马俊才，赵玉峰.基于分行维数的聚类分析研究[J].微生物学通报，1986.

[3]王颖，刘建平.基于改进遗传算法的kmeans聚类分析[J].工业控制计算机，2011.