四单元混联系统屏蔽数据的统计分析
徐晓岭, 段贵锋, 王蓉华, 顾蓓青
(1.上海对外经贸大学 统计与信息学院,上海 201620; 2.上海师范大学 数理学院,上海 200234)
四单元混联系统屏蔽数据的统计分析
徐晓岭1, 段贵锋2, 王蓉华2, 顾蓓青1
(1.上海对外经贸大学 统计与信息学院,上海 201620; 2.上海师范大学 数理学院,上海 200234)
推导了四单元混联系统屏蔽数据场合下的似然函数,并且给出了常数失效率单元和线性失效率单元所组成的四单元混联系统屏蔽数据的参数的极大似然估计,以及采用似然比构造区间估计的方法得到参数的近似区间估计.
屏蔽数据; 四单元混联系统; 极大似然估计; 近似区间估计
0 引 言
在可靠性分析中,人们往往通过分析系统的寿命数据来估计该系统中各组成单元寿命分布中的未知参数.系统寿命试验数据包括两个方面.一是失效时间;二是失效原因.理想状态下,系统的寿命数据应该包括系统失效的具体时间以及由哪个单元失效导致整个系统失效的信息.但大多数时候,导致系统失效的那个单元并不能够被准确识别出来,人们仅能够把导致系统失效的原因归结为某些单元所组成的一个集合,系统真正失效的原因被屏蔽掉了.在现实生活中,由于故障诊断和故障检测所需的费用昂贵,特别是在现代系统中越来越多地采用模块化设计,引起系统失效的确切单元通常都是未知的.在对计算机或集成电路等进行系统可靠性研究时,也会遇到相类似的屏蔽问题.导致屏蔽发生的原因很多,如:经费的不足、时间的限制、记录的错误、诊断工具的缺乏,及某些单元失效所带来的破坏性后果等.这使得屏蔽数据的统计分析成为近年来研究的热点问题,许多学者做了很好的工作,并取得了一系列研究成果,具体见文献[1-21].

图1 四单元混联系统
值得指出的是,随着系统的功能越来越完善,其构成也越来越复杂,例如航空电源系统或雷达系统等,不再是单纯的串联或并联系统,而更多的是多单元的混联复杂系统,且常常伴有屏蔽现象发生.关于由4个单元组成的系统,除了4个单元全部串联和4个单元全部并联外,系统还有6种不同的构成方式,将其统称为四单元混联系统.图1即为4个单元组成的混联系统的一种.
本文作者详细推导了如图1所示的四单元混联系统屏蔽数据场合下的似然函数,并且给出了常数失效率单元和线性失效率单元所组成的四单元混联系统屏蔽数据的参数的极大似然估计,并采用似然比构造区间估计的方法得到参数的近似区间估计.
1 四单元混联系统屏蔽数据的似然函数
在建立模型之前,先给出一些基本假设:
假设1 系统由4个独立单元混联而成;
假设2 屏蔽的发生与失效原因和时间无关(即独立);


考虑将n个四单元混联系统进行寿命试验.记Tij表示第i个系统中第j个单元的寿命,其观察值为tij,i=1,2,…,n,j=1,2,3,4.则第i个系统的寿命Ti为:
Ti=min[max(Ti1,Ti2),max(Ti3,Ti4)].
其观察值为ti,i=1,2,…,n.令Si为引起第i个系统失效的单元集合,其观察值为si,i=1,2,…,n.若si中只由一个单元组成,则表明引起第i个系统失效的原因是确切的;若si中的单元数大于一个,则表明引起第i个系统失效的原因是未知的,即引起第i个系统失效的单元寿命数据被屏蔽了.

现在考虑第i个系统:
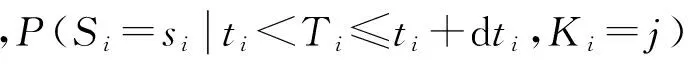
因此,

其中,P(ti 于是可以分别给出各单元失效是导致第i个系统失效的确切原因的概率: Pi1=P(ti Pi2=P(ti Pi3=P(ti Pi4=P(ti 记 fi1=f1(ti)F2(ti)[1-F3(ti)F4(ti)],fi2=F1(ti)f2(ti)[1-F3(ti)F4(ti)], fi3=[1-F1(ti)F2(ti)]f3(ti)F4(ti),fi4=[1-F1(ti)F2(ti)]F3(ti)f4(ti), 根据假设2,屏蔽的发生与失效原因和时间无关,即对于j,j′∈si有: 现在考虑n个四单元混联系统进行定时截尾寿命试验.定时截尾时间τ,这时共有r个系统失效,其次序失效时间分别为t1,t2,…,tr.此时似然函数可表示为: 其中,C>0为正常数,T为四单元混联系统的寿命. 易见,如果考虑n个四单元混联系统进行定数截尾寿命试验.定数截尾数为r,其次序失效时间分别为t1,t2,…,tr.此时似然函数可表示为: 其中,τ=max(t1,t2,…,tr). 设单元1的寿命为X,单元2的寿命为Y,单元3的寿命为Z,单元4的寿命为K,它们的失效率同为常数α,X,Y,Z,K相互独立,系统的寿命记为T,则T=min[max(X,Y),max(Z,K)]. 对于t≥0,P(T>t)=P(max(X,Y)>t)P(max(Z,K)>t)=e-2αt(2-e-αt)2. 2.1 全样本场合下的统计分析 在全样本场合下的对数似然函数为: 给定不同的样本容量n,及ni,i=1,2,…,14和参数真值的情况下,通过1 000次的Monte-Carlo模拟,得到参数α的极大似然估计的均值和均方误差,在给定置信水平0.95下得到参数α和近似区间估计的平均上限、平均下限以及1 000次模拟真值落在区间估计外面的个数,模拟结果表明极大似然估计以及近似区间估计的精度还是令人满意的. 例1 取样本容量n=38,n1=6,n2=4,n3=5,n4=4,n5=1,n6=2,n7=1,n8=1,n9=2,n10=3,n11=2,n12=1,n13=2,n14=2,4个单元的失效率同取为α=1,通过Monte-Carlo模拟产生38个失效数据如下: si={1}:2.0327,0.061004,0.35403,0.57617,1.1416,2.1044;si={2}:0.40628,0.19919,1.3348,0.5073;si={3}:0.78044,0.35211,0.6749,1.1586,0.44911;si={4}:0.71715,1.7075,0.86229,0.043607;si={1,2}:0.41627;si={1,3}:0.08604,0.2081;si={1,4}:0.57083;si={2,3}:1.8555;si={2,4}:0.33451,1.9864;si={3,4}:0.42826,0.65081,0.12387;si={1,2,3}:0.51431,1.242;si={1,2,4}:1.0934;si={1,3,4}:1.3014,1.331;si={2,3,4}:1.1799,1.0782;si={1,2,3,4}:1.5512,0.69633. 2.2 截尾样本场合下的统计分析 2(n-r)ατ+2(n-r)ln(2-e-ατ). 类似地,可用似然比的方法给出参数α的近似区间估计. 给定不同的样本容量n,和定数截尾数r,ri,i=1,2,…,14和参数真值的情况下,通过1 000次的Monte-Carlo模拟,得到参数α的极大似然估计的均值和均方误差,在给定置信水平0.95下得到参数α和近似区间估计的平均上限、平均下限以及1 000次模拟真值落在区间估计外面的个数,模拟结果表明极大似然估计以及近似区间估计的精度满足要求. 例2 取样本容量n=38,r=36,r1=5,r2=6,r3=6,r4=5,r5=2,r6=1,r7=1,r8=2,r9=1,r10=2,r11=1,r12=1,r13=1,r14=1,4个单元的失效率同取为α=1,通过Monte-Carlo模拟产生36个失效数据如下: si={1}:1.4193,0.2747,1.2822,0.8280,0.0654; si={2}:1.0330,1.3849,1.5964,1.5312,0.5222,1.6606; si={3}:1.1026,0.4690,0.5532,1.0306,1.0851,1.2903; si={4}:0.4033,1.7213,0.2125,0.7960,0.9508;si={1,2}:0.7352,0.5709; si={1,3}:0.6101;si={1,4}:0.7919;si={2,3}:0.3400,0.5037; si={2,4}:0.6608;si={3,4}:0.8442,0.9803;si={1,2,3}:0.3726; si={1,2,4}:1.0369;si={1,3,4}:0.7288;si={2,3,4}:1.2013;si={1,2,3,4}:0.8148. 设单元1的寿命为X,单元2的寿命为Y,单元3的寿命为Z,单元4的寿命为K,它们的失效率都为βt,X,Y,Z,K相互独立,系统的寿命记为T,则T=min[max(X,Y),max(Z,K)]. 3.1 全样本场合下的统计分析 在全样本数据下对数似然函数为: 类似地,可用似然比的方法给出参数α的近似区间估计.给定不同的样本容量n,及ni,i=1,2,…,14和参数真值的情况下,通过1000次的Monte-Carlo模拟,得到参数α的极大似然估计的均值和均方误差,在给定置信水平0.95下得到参数α和近似区间估计的平均上限、平均下限以及1000次模拟真值落在区间估计外面的个数,模拟结果表明极大似然估计以及近似区间估计的精度满足要求. 例3 取样本容量n=38,n1=6,n2=4,n3=5,n4=4,n5=1,n6=2,n7=1,n8=1,n9=2,n10=3,n11=2,n12=1,n13=2,n14=2,4个单元的失效率同取为βt=t,通过Monte-Carlo模拟产生38个失效数据如下: si={1}:2.0327,0.061004,0.35403,0.57617,1.1416,2.1044;si={2}:0.40628,0.19919,1.3348,0.5073;si={3}:0.78044,0.35211,0.6749,1.1586,0.44911;si={4}:0.71715,1.7075,0.86229,0.043607;si={1,2}:0.41627;si={1,3}:0.08604,0.2081;si={1,4}:0.57083;si={2,3}:1.8555;si={2,4}:0.33451,1.9864;si={3,4}:0.42826,0.65081,0.12387;si={1,2,3}:0.51431,1.242;si={1,2,4}:1.0934;si={1,3,4}:1.3014,1.331;si={2,3,4}:1.1799,1.0782;si={1,2,3,4}:1.5512,0.69633. 3.2 截尾样本场合下的统计分析 对数似然函数为: 类似地,可用似然比的方法给出参数α的近似区间估计.给定不同的样本容量n,和定数截尾数r,ri,i=1,2,…,14和参数真值的情况下,通过1 000次的Monte-Carlo模拟,得到参数α的极大似然估计的均值和均方误差,在给定置信水平0.95下得到参数α和近似区间估计的平均上限、平均下限以及1000次模拟真值落在区间估计外面的个数,模拟结果表明极大似然估计以及近似区间估计的精度满足要求. 例4 取样本容量n=38,r=37,r1=2,r2=3,r3=2,r4=3,r5=2,r6=3,r7=3,r8=2,r9=3,r10=3,r11=3,r12=2,r13=3,r14=2,4个单元的失效率同取为βt=2t,通过Monte-Carlo模拟产生37个失效数据如下: si={1}:0.9450,0.6555;si={2}:0.6093,0.6055,0.4182;si={3}:0.3874,0.3345;si={4}:0.2879,1.8960,0.7146;si={1,2}:1.4526,0.6033;si={1,3}:0.5715,0.9877,0.0242;si={1,4}:1.0173,0.5948,1.6265;si={2,3}:0.9140,0.6306;si={2,4}:1.7371,1.0492,0.2713;si={3,4}:0.7639,0.1641,1.0685;si={1,2,3}:1.4754,0.4533,1.1277;si={1,2,4}:1.0529,1.9911;si={1,3,4}:1.0176,0.4860,1.4511;si={2,3,4}:1.3909,0.5437;si={1,2,3,4}:1.0582. [1] Usher J S,Hodgson T J.Maximum likelihood analysis of component reliability using masked system life-test data [J].IEEE Transactions on Reliability,1988,37(5):550-555. [2] Doganaksoy N.Interval estimation from censored & masked system-failure data [J].IEEE Transactions on Reliability,1991,40(3):280-286. [3] Lin Dennis K J,Usher J S,Guess F M.Exact maximum likelihood estimation using masked system data [J].IEEE Transactions on Reliability,1993,42(4):631-635. [4] Reiser B,Guttman I,Lin Dennis K J,et al.Bayesian inference for masked system lifetime data [J].Appl Statist,1995,44(1):79-90. [5] Usher J S.Weibull component reliability—prediction in the presence of masked data [J].IEEE Transactions on Reliability,1996,45(2):229-232. [6] Lin Dennis K J,Usher J S,Guess F M.Bayes estimation of component-reliability from masked system-life data [J].IEEE Transactions on Reliability,1996,45(2):233-237. [7] Sarhan A M.Reliability estimations of components from masked system life data [J].Reliability Engineering and System Safety,2001,74:107-113. [8] Sarhan A M.The bayes procedure in exponential reliability family models using conjugate convex tent prior family [J].Reliability Engineering and System Safety,2001,71:97-102. [9] Sarhan A M.Estimation of system components reliabilities using masked data [J].Applied Mathematics and Computation,2003,136:79-92. [10] Sarhan A M,Ahmed H.El-Bassiouny.Estimation of components reliability in a parallel system using masked system life data [J].Applied Mathematics and Computation,2003,138:61-75. [11] Sarhan A M,Awad I El-Gohary.Estimations of parameters in Pareto reliability model in the presence of masked data [J].Reliability Engineering and System Safety,2003,82:75-83. [12] Sarhan A M.Parameter Estimations in linear failure rate model using masked data [J].Applied Mathematics and Computation,2004,151:233-249. [13] Sarhan A M.Parameter Estimations in a general hazard rate model using masked data [J].Applied Mathematics and Computation,2004,153:513-536. [14] Sarhan A M.Bayes estimations for reliability measures in geometric distribution model using masked system life test data [J].Computational Statistics and Data Analysis,2008,52(4):1821-1836. [15] Awad El-Gohary.Bayesian estimation of the parameters in two non-independent component series system with dependent time failure rate [J].Applied Mathematics and Computation,2004,154:41-51. [16] Hutto D E,Mazzuchi T,Sarkani S.Analysis of reliability using masked system life data [J].International Journal of Quality & Reliability Management,2009,26(7):723-739. [17] Tsai H F,Wan L W.Accelerated life tests for weibull series systems with masked data [J].IEEE Transactions on Reliability,2011,60(3):557-569. [18] Hou H L,Jiang Y W,Shi Y M.Parameter estimations in BurrXII model using masked data [J].Chin Quart J of Math,2011,26(2):251-255. [19] Xu A C,Tang Y C.Bayesian analysis of pareto reliability with dependent masked data [J].IEEE Transactions on Reliability,2009,58(4):583-588. [20] Wang R H,Xu X L,Gu B Q.The statistical analysis of parallel system for Type-I censored test using masked data [C].Recent Advance in Statistics Application and Related Areas-2nd Conference of the International Institute of Applied Statistics Studies,Qingdao,China,July 24-29,2009,789-795. [21] Xu A C,Tang Y C.An overview on statistical analysis for masked system lifetime data [J].Chinese Journal of Applied Probability and Statistics,28(4):380-388. (责任编辑:冯珍珍) Statistical analysis of four-unit hybrid system for masked data Xu Xiaoling1, Duan Guifeng2, Wang Ronghua2, Gu Beiqing1 (1.School of Statistics and Information,Shanghai University of International Business and Economics,Shanghai 201620,China; 2.College of Mathematics and Science,Shanghai Normal University,Shanghai 200234,China) The likelihood function of four-unit hybrid system is deduced based on masked data.The maximum likelihood estimates of parameters are proposed for hybrid system composed of four units with constant failure rate and linear failure rate based on masked data.Besides,the approximate interval estimates of parameters are obtained by using likelihood ratio to construct interval estimate. masked data; four-unit hybrid system; maximum likelihood estimate; approximate interval estimate 2015-07-01 上海市教育委员会科研创新重点项目(14ZZ155) 徐晓岭(1965-),男,教授,主要从事应用统计方面的研究.E-mail:xlxu@suibe.edu.cn O 213 A 1000-5137(2017)02-0178-08

2 单元失效率同为常数的四单元混联系统屏蔽数据的统计分析

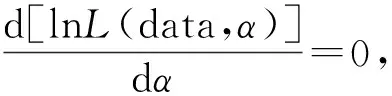







3 单元失效率同为过原点的线性函数的四单元混联系统屏蔽数据的统计分析









