齿轮箱壳体及轴承支撑刚度对风电机组传动链固有频率的影响*

文 | 张静，姜少辉，盛秋刚，董振华

技术

齿轮箱壳体及轴承支撑刚度对风电机组传动链固有频率的影响*

文 | 张静，姜少辉，盛秋刚，董振华

近几十年，随着石油、天然气等能源的枯竭以及人们对于环境问题的日益重视，全球风电总装量不断扩增，根据世界风能协会掌握的数据，到2020年全球风电容量将接近239GW，足够满足世界3%的用电。我国从2003年以来装机容量快速增长，到2010年底我国风电装机容量已经跃居世界第一，成为全球风电装机速度最快的国家。

风电机组按照传动形式可划分为：多级齿轮传动型、半直驱型和直驱型三大类。大部分制造商采用了双馈感应发电机以及多级增速齿轮箱的机组类型，如Vestas，Gamesa，GE wind，REpower。这种风电机组传动链包括叶片、轮毂、主轴（主轴承）、齿轮箱、减震装置、联轴器、发电机等。由于风电机组传动链系统的工作转速范围广，激励频率带较宽，在时变外部载荷和内部载荷的共同作用下易与系统发生共振，造成整个风电机组的失效和重大安全事故，因此风电机组传动链系统的动态特性研究对于兆瓦级风电机组的高可靠运行有着十分重要的意义。

国内风电机组传动链的研究相对国外较为滞后，2005年朱才朝等人建立了风电机组多级齿轮传动的齿轮—传动轴—箱体的耦合非线性动力学模型，对风电机组传动链中的齿轮传动系统进行动态特性分析。2009年顾佥利用多体动力学软件SIMPACK建立了两级行星一级平行轴的风电机组传动链动力学模型，结合坎贝尔图和能量图频率分析，并通过扫略计算，对转动方向内的固有频率一一进行排除，较为完整地进行了传动链的共振分析。

传动链的拓扑建模

在既往的风电机组传动链共振分析中，轴类零件、叶片、行星架按照柔性体设置，轮毂、行星架、齿轮箱外壳、主机架、联轴器、发电机支架、主机架均按照刚体设置， 其中轮毂采用有限元软件计算其旋转刚度，并通过FE13施加，联轴器（包括刹车盘）分成四段，每段之间的扭转刚度由厂家提供。在GL规范2010版中，针对传动链建模做出了更为详细的规定，见表1。

表1 主要传动链部件的建模要求

图1 传动链拓扑关系

图2 主节点的设置（前面）

图3 主节点的设置（后面）

由表1可得，轴类零件、行星架、齿轮箱外壳、主机架推荐柔性体，轴承推荐6×6阶刚度矩阵。柔性体越多，计算时间越长，因此在保证结果正确性的前提下，应该尽量减少柔性体的个数。同时齿轮箱内的轴承矩阵往往很难从供应商处获得，因此承受径向力的圆柱滚子轴承常采用93号力元来模拟轴承支撑刚度。本文建立了三点支撑传动链模型，拓扑关系见图1，对比了齿轮箱外壳为刚体和柔性体下，传动链旋转面内固有频率的变化；同时对比了齿轮箱内轴承支撑刚度对传动链转动平面内固有频率的影响，完成齿轮箱部分参数的敏感性分析，对风电机组传动链共振分析有一定的指导意义。

齿轮箱外壳的柔性化

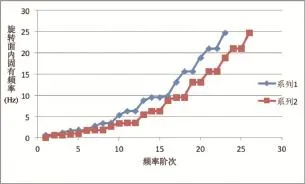
图4 刚、柔齿轮箱传动链固有频率对比（30Hz以内）

图6 刚、柔齿轮箱传动链固有频率对比（30Hz之外）

图5 不同轴承刚度传动链固有频率对比（30Hz以内）

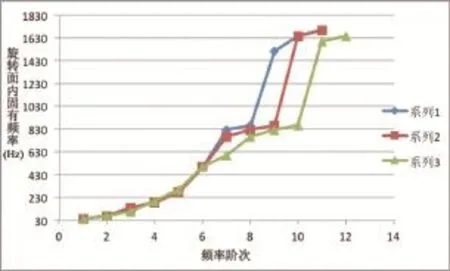
图7 不同轴承刚度传动链固有率对频比（30Hz之外）

为了对比柔性齿轮箱对传动链固有频率的影响，分别将齿轮箱外壳设置为刚体和柔性体。在Ansys软件中，采用子结构分析的方法，将所有单元凝结于几个超单元，得到单元的质量矩阵和刚度矩阵，将fle.sub和fle.cdb文件导入SIMPACK软件中进行柔性化，得到fle.fbi文件。

图2和3给出了齿轮箱外壳主节点的设置位置，分别为和齿轮轴的连接轴承处和行星架的连接轴承处，和主机架接触的弹性支撑处。

齿轮箱外壳刚度和轴承支撑刚度对风电机组频率的影响

一、刚性和柔性齿轮箱外壳对应的风电机组转频

按照图1对应的拓扑关系，搭建传动链模型，其中轴类零件、叶片、行星架按照柔性体设置，其余零件按照刚体设置。在比较分析时，齿轮箱内轴承支撑刚度设置为1E12N/m。根据GL2010传动链共振分析需要三个状态：切入、额定、切出，由于三种状态下风电机组传动链频率差别很微小，因此选取额定风速为分析条件。轮毂中心输入额定扭矩，转子与定子之间输入发电机功率曲线，进行动平衡计算，直到风电机组达到平衡状态。保持平衡状态，进行模态分析，结合阵型和各个部件的能量图得到传动链转动平面内固有频率。图4、图5给出了刚性齿轮箱壳体和柔性齿轮箱壳体传动链转动平面内固有频率。

其中系列1代表齿轮箱外壳为刚体时，传动链转动平面内固有频率，系列2代表齿轮箱外壳为柔性体时，传动链转动平面内固有频率。

二、不同轴承支撑刚度对应的风电机组转频

齿轮箱外壳设置为刚体，分别计算了齿轮箱内轴承支撑刚度为1E12 N/m、1E10 N/m、1E8 N/m时，传动链的转动平面内的固有频率，见图6、图7。

其中系列1代表轴承刚度为1E12 N/m时传动链转动平面内固有频率，系列2代表轴承刚度为1E10N/m时传动链转动平面内固有频率，系列3代表轴承刚度为1E8 N/m时传动链转动平面内固有频率。

结论

从图4可以看到5Hz－30Hz，柔性壳体和刚性壳体的频率差别很小，相近频率的对比，最大差别是0.4%。5Hz以内，柔性壳体的固有频率为12阶，刚性壳体的固有频率为9阶，多出的频率分别为0.051Hz、0.872Hz、0.995Hz。从图4、图5可以看出30Hz以上的频率，前两阶基本吻合，后续频率的差别比较大，柔性壳体的频率偏小，并且高阶频率个数偏少。综上可知，由于30Hz以内的频率主要代表叶片的转动频率，因此齿轮箱的刚度对此范围内的频率影响不大；30Hz以外的频率，代表传动链其他部件的频率，齿轮箱的刚度对此范围内的频率影响较大。所以柔性壳体虽然会延长计算时间，但是计算结果和刚性壳体有明显的差别，建议采用柔性壳体参与计算。

从图6可以得出30Hz以内，支撑刚度的变化对频率的影响非常微小，很多阶次甚至数据完全吻合，这也恰恰表明齿轮箱内的参数变化对叶片固有频率是基本没有影响的。从图7可以看出，轴承支撑刚度为1E12 N/m和1E10 N/m时，频率的差别微小，相近频率的偏差仅为0.005%，只有在高频处，前者多出一阶频率；当轴承支撑刚度为1E8 N/m时，频率与前两者部分吻合，低阶和高阶频率差别较大。所以齿轮箱内轴承的支撑刚度对传动链的固有频率有一定的影响，当轴承刚度越来越大时，传动链固有频率变化不大；当轴承刚度变小时，频率变化明显。建议采用6×6阶矩阵来表达轴承刚度，从而得到准确的计算结果。

（作者单位：张静，姜少辉，董振华：华锐风电科技（集团）股份有限公司；盛秋刚：上海绿色环保能源有限公司）

摄影：李志明

上海市科学技术委员会项目“深远海上风电机组设计开发及运维相关技术研究”（项目（课题）编号：16DZ1203505）