一类Riccati方程解的性质

凌 云 ,李满枝,2

(1.海南师范大学 数学与统计学院,海口571158;2.海南省数学研究中心,海口571158)

一类Riccati方程解的性质

凌 云1,李满枝1,2

(1.海南师范大学 数学与统计学院,海口571158;2.海南省数学研究中心,海口571158)

对不能应用初等积分法求解的Riccati方程, 研究解的存在唯一性、解的最大存在区间的有界性及积分曲线的单调性和凹凸性,最后应用Bernoulli方程求解出这类Riccati方程的通解.

Riccati方程; 通解; 性质; Bernoulli方程

0 引言

在常微分方程中,有很多方程并不能用初等解法求解.例如形式上很简洁的Riccati微分方程

(1)

1 预备知识

引理[15]首先考虑导数已解出的一阶微分方程

(2)

若f(x,y)满足两个条件:

1)在矩形域R上连续;

2)关于y满足Lipschitz条件.

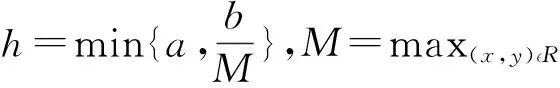
|x-x0|≤a,|x-x0|≤b.

(3)

2 定理及其证明

定理1 微分方程

(4)

过平面xoy上任意一点的积分曲线存在且唯一.

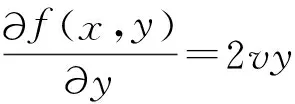
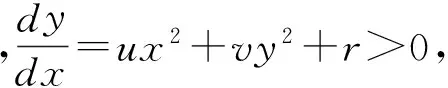
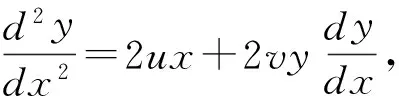
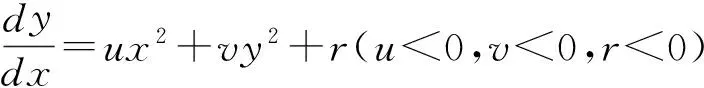
AsDh Study Group 1998: Abhisamācārika-Dharma Study Group, A Guide to the Facsimile Edition of the Abhisamācārika-Dharma of the Mahāsāghika-Lokottaravādin, Tokyo: The Institute for Comprehensive Studies of Buddhism Taisho University.

定理3 对于初值问题

此时令

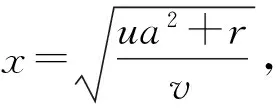
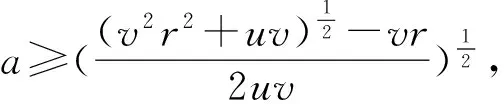
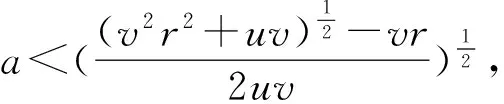
由(i)、(ii)得:

综上所述:

(5)

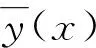
因此

(6)

式(6)为Bernoulli微分方程.若两边同时乘以z-2,则有

这时我们令f=z-1,式(6)可化为

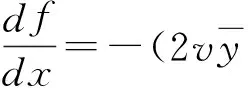
由此公式得:

即

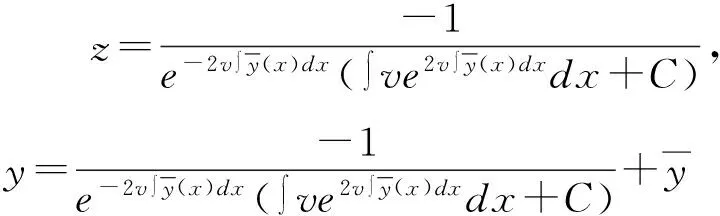
故方程的通解为

(7)

3 结论

[1]王高雄, 周之铭.常微分方程 [M].3版.北京:高等教育出版社,2006.

[2]曹恒.里卡蒂方程几种特解的判定[J].数学的理论与应用,2002,22(4): 82-84.

[3]段峰.几类可积的Riccati方程解的性质[J].中央民族大学学报(自然科学报),2016,25(2):27-29.

[4]冯录祥.一类Riccati方程的推广[J].数学的实践与认识,2003,33(5):115-119.

[5]胡建,王建明.可积Riccati微分方程的通解公式[J].河南教育学院学报(自然科学版),2007,16(2):7-8.

[6]王玉萍,卢琨,史胜楠.Riccati方程的可积条件及通积分[J].陕西科技大学学报,2007,25(2):136-138.

[7]冯录祥.一类Riccati方程的通积分[J].渭南师范学院学报,2007,22(2):9-11.

[8]赵临龙,段峰,张兰.Riccati方程的几个性质[J].首都师范大学学报(自然科学报),2014,35(6):9-12.

[9]王建明.Riccati微分方程特解新求法的研究[J].数学的实践与认识,2006,36(7):382-386.

[10]朱军辉,陈春蕊.一类里卡蒂方程解的性质[J].高师理科学刊,2012,32(9):29-30.

[11]张玮玮.一类特殊类型的Riccati方程的求解[J].安庆师范学院学报(自然科学报),2015,21(2):110-111.

[12]黄敏.用不动点定理研究方程解的存在性[J].琼州学院学报,2006,13(2):3-5.

[13]黄晓芬,杨立兵.齐次微分方程的解的存在性[J].琼州学院学报,2012,19(5):4-6.

[14]林文贤.一类三阶半线性中立型阻尼微分方程的振动性[J].海南热带海洋学院学报,2016,23(5):38-43.

[15]卡姆尼.常微分方程手册[M].北京:科学出版社,1977.

(编校：曾福庚)

The Properties of the General Solutions of the Special Riccati Equation

LING Yun1, LI Man-zhi1,2

(1.College of Mathematics and Statistics, Hainan Normal University，Haikou 571158, China2.Hainan Center for Mathematical Research,Haikou 571158, China)

As for a class of Riccati equations for which the elementary integration method cannot be used,we considered the existence and uniqueness of the solution,and the boundedness of the maximum existence interval of Riccati equation solution.We discussed the concavity, the convexity and monotonicity of the solution curves from the characteristic of the Riccati equation.Consequently, the general solutions were given by applying Bernoulli equation in the end.

Riccati equation; general solutions; properties; Bernoulli equation

格式：凌云 ,李满枝.一类Riccati方程解的性质[J].海南热带海洋学院学报,2017，24(2)：43-46.

2016-11-22

海南省自然科学基金项目(20151003);海南师范大学数学与统计学院计算数学重点学科项目(201602)

李满枝(1979-), 女, 新疆伊犁人, 海南师范大学数学与统计学院副教授,硕士,研究方向为微分方程和数值模拟.

O175.1

A

2096-3122(2017) 02-0043-04

10.13307/j.issn.2096-3122.2017.02.09