von Neumann 代数上的非线性保持*-Lie积的双射

余维燕

(海南师范大学 数学与统计学院，海口 571158)

von Neumann 代数上的非线性保持*-Lie积的双射

余维燕

(海南师范大学 数学与统计学院，海口 571158)

设M,N是复Hilbert空间H上的因子von Neumann代数,且dim H≥2.本文证明了对任意的A,B∈M，满足条件φ(AB-BA*)=φ(A)φ(B)-φ(B)φ(A)*的双射φ：M→N是一个线性或共轭线性的*-同构.

非线性保持；*-Lie积；von Neumann代数

0 引 言

在近二十年，保持算子或矩阵某些特定性质或关系不变的线性或可加映射的研究引起许多学者的关注(见文献[1-9])，所得到的结果从新的方面揭示了算子代数的代数与几何结构.最近几年，一些学者开始研究一些非线性的保持算子某些特定性质的映射(见文献[10-15]).文献[11-13]中，作者刻画了非线保持Lie乘积的映射.本文我们主要研究因子von Neumann代数上的一类非线性保持乘积XY-YX*(*-Lie积)的映射.我们知道映射X→XY-YX*也是一个Jordan*-导子([16]).

设H是复Hilbert空间.B(H)表示H上的有界线性算子，M⊆B(H)是一个von Neumann代数.如果M的中心是I,其中I是M的单位元，则称M是一个因子von Neumann代数.对任意的X，Y∈M,记{X，Y}=XY-YX*.设Msa是M的自伴算子空间，P(M)表示M的非平凡正交投影集.

1 主要结果

在这一部分，我们主要证明以下结果：

定理2.1 设H是复Hilbert空间且dimH≥2,M,N是H上的因子von Neumann代数.若对任意的A,B∈M,φ:M→N是满足条件φ(AB-BA*)=φ(A)φ(B)-φ(B)φ(A)*的双射(非线性)，则φ是一个线性或共轭线性*-同构.

为了证明定理2.1，需要证明一些引理.以下设M，N是复Hilbert空间H(dimH≥2)上的因子von Neumann代数，φ:M→N是双射且对任意的A，B∈M满足条件

φ(AB-BA*)=φ(A)φ(B)-φ(B)φ(A)*.

(1)

引理2.1φ(0)=0；φ(Msa)=Nsa;φ(I)=I;φ(P(M))=P(N).

证明 因为φ是满射，则有B0∈M使得φ(B0)=0.从而

φ(0)=φ(0B0-B00*)=φ(0)φ(B0)-φ(B0)φ(0)*=0.

对任意的B∈M,有φ(I)φ(B)-φ(B)φ(I)*=φ(IB-BI*)=φ(0)=0.从而存在λ0∈/{0}使得φ(I)=φ(I)*=λ0I.设A∈Msa,则有

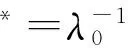
因此φ(Msa)⊆Nsa.同理,对φ-1,有Nsa⊆φ(Msa),故φ(Msa)=Nsa.

设λ∈，则对任意A∈Msa,有

φ(A)φ(λI)-φ(λI)φ(A)=φ(A(λI)-(λI)(A))=φ(0)=0.

从而由φ(Msa)=Nsa可得φ(λI)∈I,故φ(I)⊆I.同理，对φ-1可得I⊆φ(I).因此φ(I)=I.

设P∈P(N)且有A∈M使得φ(A)=P.则对A∈Msa且B∈M有

φ({A,{A,{A,B}}})={P,{P,{P,φ(B)}}}={P,φ(B)}=φ({A,B}),

由φ是满射可知{A，{A，{A，B}}}={A，B}，即对任意的B∈M,有

A3B-3A2BA+3ABA2-BA3=AB-BA.

(2)

另一方面，对任意的B∈Msa，有

φ({{A,B},A})={{P,φ(B)},P}={P,φ(B)}=φ({A,B}),

从而{{A，B}，A}={A，B}，即对任意的B∈Msa,有A2B-BA2=AB-BA.因此存在λ1∈,使得A2=A+λ1I.由此式与式(2)，对任意的B∈M，有4λ1(AB-BA)=0.

(3)

因为φ(I)=I且φ(A)=P∉I,则存在B∈M,使得AB-BA≠0.由式(3)可得λ1=0,从而A=A2=A*∈P(M).同理,对φ-1,可证得φ(P(M))⊆P(N).从而φ(P(M))=P(N).证毕.

现在，我们选择一个投影P1∈P(M)且P2=I-P1.设Qi=φ(Pi),i=1，2.由引理2.1,Qi∈P(N),i=1,2.因为对任意的B∈Msa,有{Q1，φ(B)}={φ(B),Q2}，故Q2=I-Q1.记Mij=PiMPj且Nij=QiNQj,其中i，j=1,2.则有以下引理.

引理2.2 设Xll∈Mll.若对任意的Til∈Mil,有TilXll=0,则Xll=0.

证明 显然.

引理2.3 设i,j=1,2且i≠j.则有φ(Mij)=Nij.

证明 设A∈Mij,由A={Pi,A}={Pi，{Pi,A}}可得

φ(A)=Qiφ(A)Qj-Qjφ(A)Qi

与

φ(A)=Qiφ(A)Qj+Qjφ(A)Qi,

以上两式相加可得φ(A)=Qiφ(A)Qj.从而有φ(Mij)⊆Nij.对于φ-1，同理可证Nij⊆φ(Mij).因此φ(Mij)=Nij.证毕.

引理2.4 设i,j,k,l=1，2.则对任意的Aij∈Mij与Bkl∈Mkl,有φ(Aij+Bkl)=φ(Aij)+φ(Bkl).

φ(TX-XT*)=φ(TAij-AijT*)+φ(TBkl-BklT*)

(4)

与

φ(TX-TX*)=φ(AijT-TAij*)+φ(BklT-TBkl*).

(5)

情形1 若i=j且k≠l,则有k=i,l≠i或l=i,k≠i.

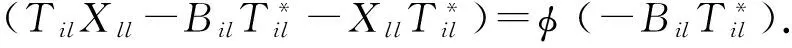
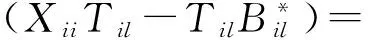
从而

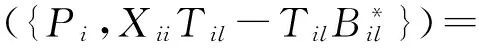
故对任意的Til∈Mil,有φ(XiiTil)=φ(AiiTil),从而Xii=Aii.因此φ(Aii+Bil)=φ(Aii)+φ(Bil).

对l=i,k≠i,可类似证明结论也成立.

情形2 若i≠j且k≠l,则k=j,l=i或k=i,l=j.

对k=j,l=i,在式(4)中取T=Pi,可得φ(Xij-Xji)=φ(Aij)+φ(-Bji).从而φ({Pi,Xij-Xji})=φ({Pi,Aij})+φ({Pi-Bji}).即,

φ(Xij+Xji)=φ(Aij)+φ(Bji).

(6)

在式(5)中分别用Pi和Pj代替T，可得

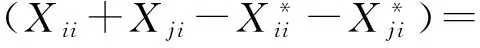
与

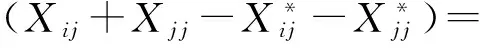
由此可得Xji=Bji且Xij=Aij.由式(6)可知，φ(Aij+Bji)=φ(Aij)+φ(Bji).

当k=i,l=j，有

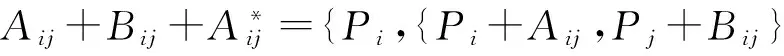
由情形1，及φ(Mij)=Nij,有

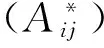
从而φ(Aij+Bij)=φ(Aij)+φ(Bij).

情形3 若i=j且k=l,则i=k或i≠k.

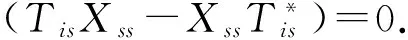
φ(Xii)=φ(Aii)+φ(Bii).

(7)

在式(5)中用Tis替换T，则有

φ(XiiTis)=φ(AiiTis)+φ(BiiTis)=φ(AiiTis+BiiTis),

从而Xii=Aii+Bii.由此式与式(7)可得φ(Aii+Bii)=φ(Aii)+φ(Bii).

当i≠k,在式(4)中取T=Pi，则φ(Xik-Xki)=0,故Xik=Xki=0,从而X=Xii+Xkk.在式(4)与式(5)中分别取T=Tik，可得

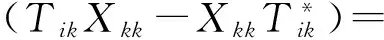
与

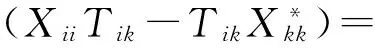
从而对任意的Tik∈Mik,有

(8)

与

(Xii-Aii)Tik=Tik(Xkk-Bkk)*.

(9)

由式(8)或得Xkk=Bkk,再由式(9)可得Xii=Aii.故φ(Aii+Bkk)=φ(Aii)+φ(Bkk).证毕.

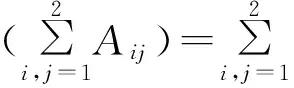
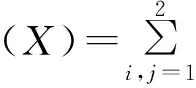
(10)

在式(10)中取T=P1，由引理2.3可得

φ(X12-X21)=φ(A12)+φ(-A21)=φ(A12-A21),

由此可得X12=A12,X21=A21,故X=X11+A12+A21+X22.在式(10)中分别用T12与T21替换T，则有

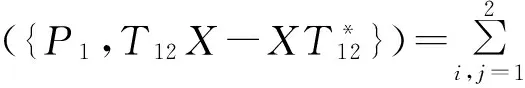
与

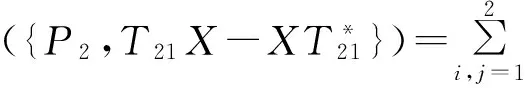
即

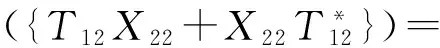
与

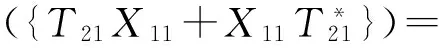
因此，对任意的T12∈M12，有

(11)

且对任意的T21∈M21，有

(12)

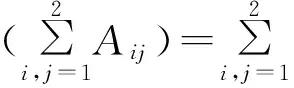
引理2.6 对任意的A，B∈M,有φ(A+B)=φ(A)+φ(B).

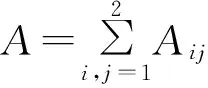
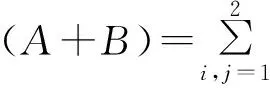
由引理2.6及φ(I)=I可知，存在可加的双射ρ∶→，使得对任意的λ∈且ρ(1)=1，有φ(λI)=ρ(λ)I.

引理2.7 对任意的A∈M与λ∈,有φ(λA)=ρ(λ)φ(A).

证明 设x∈是任意实数，则有

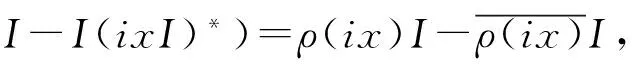
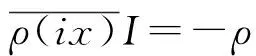
-2ρ(x)I=φ((ixI)(iI)-(iI)(ixI)*)=2ρ(ix)ρ(i)I.

从而对任意的x∈,有

ρ(ix)ρ(i)=-ρ(x).

(13)

对任意的A∈M,有

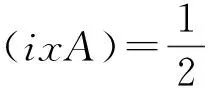
特别，有φ(-iA)=-ρ(i)φ(A)与φ(xA)=ρ(ix)φ(-iA).由此结果与式(13)可知，对任意的x∈与A∈M,有φ(xA)=ρ(x)φ(A).因此对任意的λ=x+iy∈(x,y∈)及A∈M,有

φ(λA)=φ(xA)+φ(iyA)=ρ(x)φ(A)+ρ(iy)φ(A)=ρ(λ)φ(A).

引理2.8φ是线性映射或共轭线性映射.

证明 由引理2.6与2.7，只需证ρ是恒等映射或共轭恒等映射.由ρ的可加性可知，对任意有理数r，有ρ(r)=r.由引理2.6可知，对任意的λ,β∈,有ρ(λβ)=ρ(λ)ρ(β)，又因为φ(Msa)=Nsa,则若ρ(λ)>0当且仅当λ>0.从而对有理数r与实数x,y，当|x-y|

定理2.1的证明 由ρ(i)2=-1,对任意的A，B∈M,由引理2.7可知，

再由定理2.1所给条件可知，

φ(AB-BA*)=φ(A)φ(B)-φ(B)φ(A)*.

由以上两式及引理2.6可知,对任意的A，B∈M，有

φ(AB)=φ(A)φ(B)

(14)

与

φ(BA*)=φ(B)φ(A)*.

(15)

在式(15)中取B=I，可得φ(A*)=φ(A)*,从而φ是一个线性或共轭线性*-同构.

[5]M.Choi,A.Jafarian,H.Radjavi.Linearmapspreservingcommutativity[J].LinearAlgebraAppl., 1987, 87: 227-241.

[7]W.Y.YU,J.H.Zhang.LietriplederivationsofCSLalgebras[J].IntTheorPhys., 2013, 52: 2118- 2127.

[8]W.Y.YU,J.H.Zhang.σ-biderivationandσ-commutingmapsonnestalgebras[J].ActaMath.Sinica, 2007, 50(6): 1391-1396.

[9]W.Y.YU,J.H.Zhang.Jordanderivationsoftriangularalgebras[J].LinearAlgebraAppl., 2006, 419(1): 251-255.

[10]L.Molnár,P.Semrl.Nonlinearcommutativitypreservingmapsonself-adjointoperators[J].Q.J.Math., 2005, 56(4): 589-595.

[11]P.Semrl.Non-linearcommutativitypreservingmaps[J].ActaSci.Math.(Szeged), 2005(71): 781- 819.

[12]J.H.Zhang,F.J.Zhang.NonlinearmapspreservingLieproductsonfactorronNeumannalgebras[J].LinearAlgebraAppl., 2008, 429(1): 18-30.,

[13]J.C.Hou,K.He,X.L.Zhang.Nonlinearmapspreservingnumericalradiusofindefiniteskewprod-uctsofoperators[J].LinearAlgebraAppl., 2009, 430(8/9): 2240-2253.

[14]W.Y.YU,J.H.Zhang.NonlinearLiederivationsoftriangularalgebras[J].LinearAlgebraAppl., 2010, 432(11): 2953-2960.

[15]W.Y.YU,J.H.Zhang.Nonlinear*-LiederivationsonfactorvonNeumannalgebras[J].LinearAlgebraAppl., 2012, 437(8): 1979-1991.

(编校：吴炎)

Nonlinear Maps Preserving *-Lie Productson Factor von Neumann Algebras

YU Wei-yan

(College of Mathematics and Statistics, Hainan Normal University, Haikou 571158, China)

Let M and N be factor von Neumann algebras acting on a complex Hilbert space H with dim H≥2.We prove that every bijective map φ∶M→N satisfying φ(AB-BA*)=φ(A)φ(B)-φ(B)φ(A)*for all A,B∈M is a linear or conjugate linear *-isomorphism.

nonlinear preserver;*-Lie products; von Neumann algebra.

格式：余维燕.von Neumann代数上的非线性保持*-Lie积的双射[J].海南热带海洋学院学报,2017，24(2)：34-38.

2017-03-11

国家自然科学基金资助项目(11461018);海南省自然科学研究计划资助项目(20151012);海南省教育厅高校科研项目(hjkj2014-16)

余维燕(1969-),女,四川资中人,海南师范大学数学统计学院副教授,博士,研究方向为算子理论与算子代数.

O177.1

A

2096-3122(2017) 02-0034-05

10.13307/j.issn.2096-3122.2017.02.07