基于最优能量转移的混合拓扑结构研究
严 刚, 张 利, 景俊峰, 刘征宇
(1.合肥工业大学 管理学院,安徽 合肥 230009; 2.江淮汽车股份有限公司,安徽 合肥 230091; 3.合肥工业大学 机械工程学院,安徽 合肥 230009; 4.安全关键测控技术教育部工程研究中心,安徽 合肥 230009)
基于最优能量转移的混合拓扑结构研究
严 刚1,2, 张 利3,4, 景俊峰3, 刘征宇3,4
(1.合肥工业大学 管理学院,安徽 合肥 230009; 2.江淮汽车股份有限公司,安徽 合肥 230091; 3.合肥工业大学 机械工程学院,安徽 合肥 230009; 4.安全关键测控技术教育部工程研究中心,安徽 合肥 230009)
动力电池均衡是电动汽车应用中的重要技术,目前大多数的均衡拓扑结构与均衡控制策略都将电池组均衡度作为唯一的控制目标,而忽略了能量利用率。文章分析了分布式与集中式均衡拓扑的优缺点,设计出了一种能较好地提高均衡速度的混合型主动均衡拓扑结构,并提出了一种基于转移最少能量达到均衡目的的控制策略。仿真实验结果表明,混合拓扑有效且有实际应用价值,控制策略能有效提高能量利用率,减少均衡损耗。
均衡拓扑;均衡速度;均衡策略;能量损耗
0 引 言
车用锂电池在制造和使用过程中,参数差异及充放电条件的影响会造成单体电池的不一致,进而影响整个电池组的正常使用,降低电池组的使用寿命[1]。因此需要在电池组使用过程中对其进行均衡控制。
均衡控制主要通过均衡拓扑与控制策略来实现。目前均衡拓扑主要分为无源均衡拓扑与有源均衡拓扑。无源均衡拓扑大多通过飞跨电容加高速开关来实现能量转移,但能量转换速度慢、瞬间冲击电流很大,容易出现电磁干扰[2-3];有源均衡拓扑是模拟开关电源的原理设计出来的,也是目前研究最多的均衡拓扑,其结构属于储能式均衡电路,理论上不存在能量损失,也不需要复杂的控制电路和额外的开关网络[4-5]。
有源均衡拓扑以集中式均衡与分布式均衡为主[6],这两类均衡拓扑各有优缺点。本文将分别对其中的典型电路进行分析,针对它们的优缺点设计出一种新型均衡拓扑结构。实验证明,本文设计出的均衡拓扑能有效地降低电池组的不一致性,提高电池组的均衡效率。
当前实际应用的控制策略大多采用基于电压的均衡方法,但该方法有很大的局限性,即端电压不能完全准确地表示电池能量状态。
本文提出一种最优能量转移的控制策略,并改进了基于电压的均衡方法,提高了均衡的可靠性与有效性。
1 典型均衡拓扑优缺点分析
1.1 集中式均衡拓扑
集中式均衡拓扑是将拓扑通过一个多输出的变压器,将电压高的电池中的能量传递到电压最低的电池中。其典型电路为文献[7]提出的集中式均衡结构,如图1所示。
该拓扑结构的变压器原边接电池组,副边与单体电池相连并采用双向开关。通过变压器实现单体电池与电池组间的能量交换,由于双向开关的作用,在电池组充电与放电过程中均能起到均衡作用。该拓扑结构均衡速度快、均衡效率高、控制简单,但也存在着不易扩展、副边绕组多、变压器设计困难等缺点。因此该类拓扑结构适用于串联单体电池较少的场合。
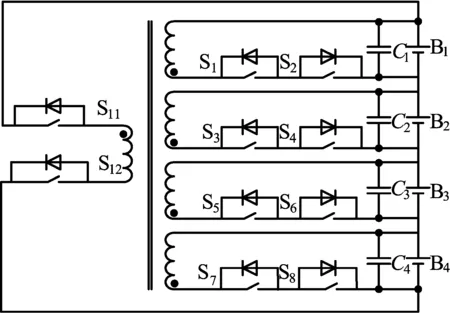
图1 集中式均衡拓扑结构
1.2 分布式均衡拓扑
文献[8]提出的基于升降压变换器的分布式均衡拓扑典型电路如图2所示。该拓扑可实现充电和放电情况下的均衡,同时适用于大功率的设计,高频条件下工作可大大减小设备的体积,方便在狭小的空间内进行布局,模块化强。但是当串联电池组内不均衡的电池出现位置不相邻时,则能量传输路径长,均衡速度慢,效率低下。
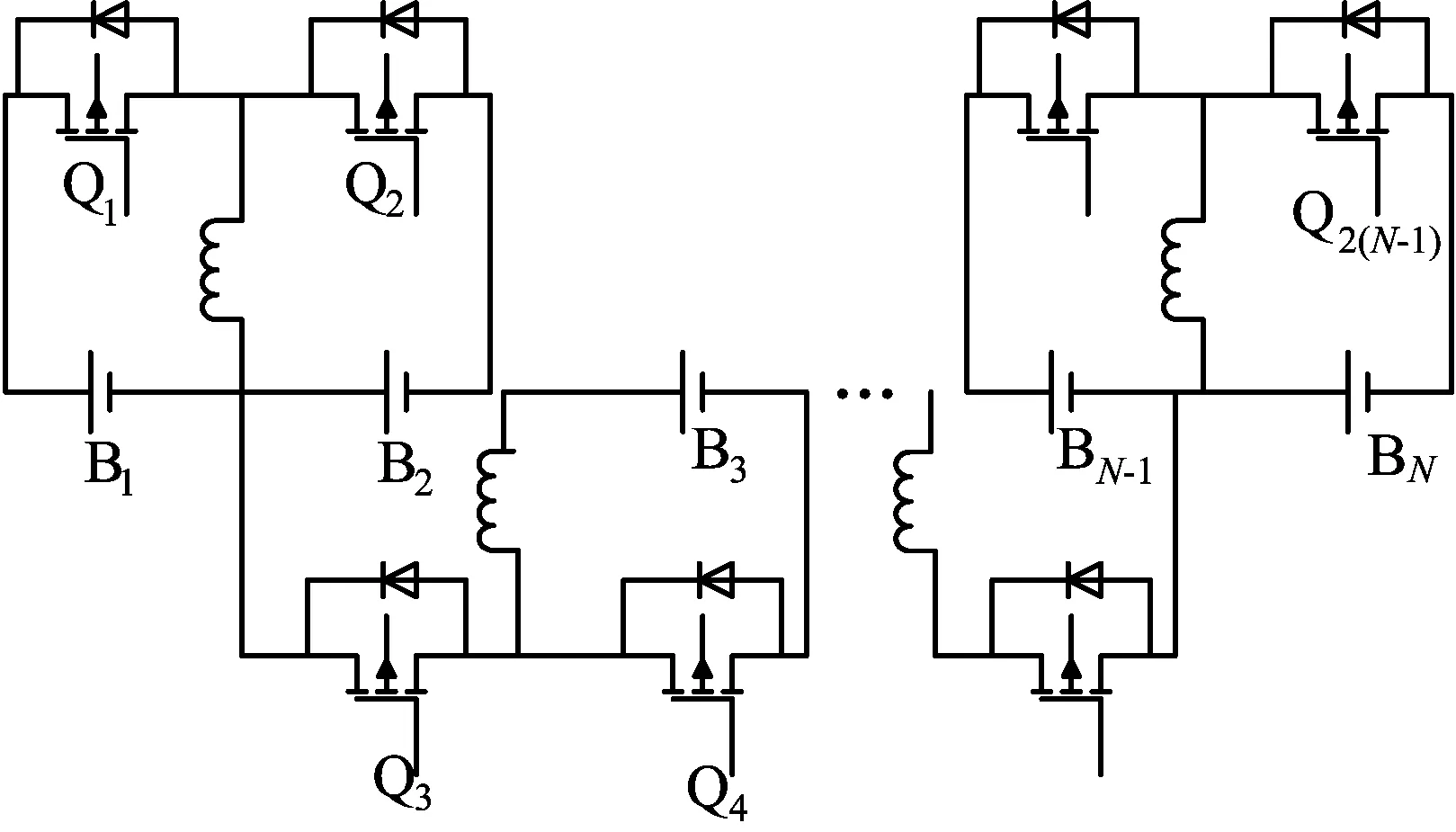
图2 分布式均衡拓扑结构
2 混合均衡拓扑结构分析
结合集中式和分布式均衡拓扑结构的优缺点,本文通过改进提出了混合均衡拓扑结构,如图3所示。该结构以3节电池为1组,组内采用基于Buck-Boost电路的改进型均衡拓扑结构,可以实现3节单体电池中任意两节电池之间的均衡。每3节电池为1组,组与组之间采用集中式均衡拓扑结构,可以实时地进行任意两组之间的均衡。并且组间均衡与组内均衡可以同时进行,因此能够直接均衡的单体数量达到最大。
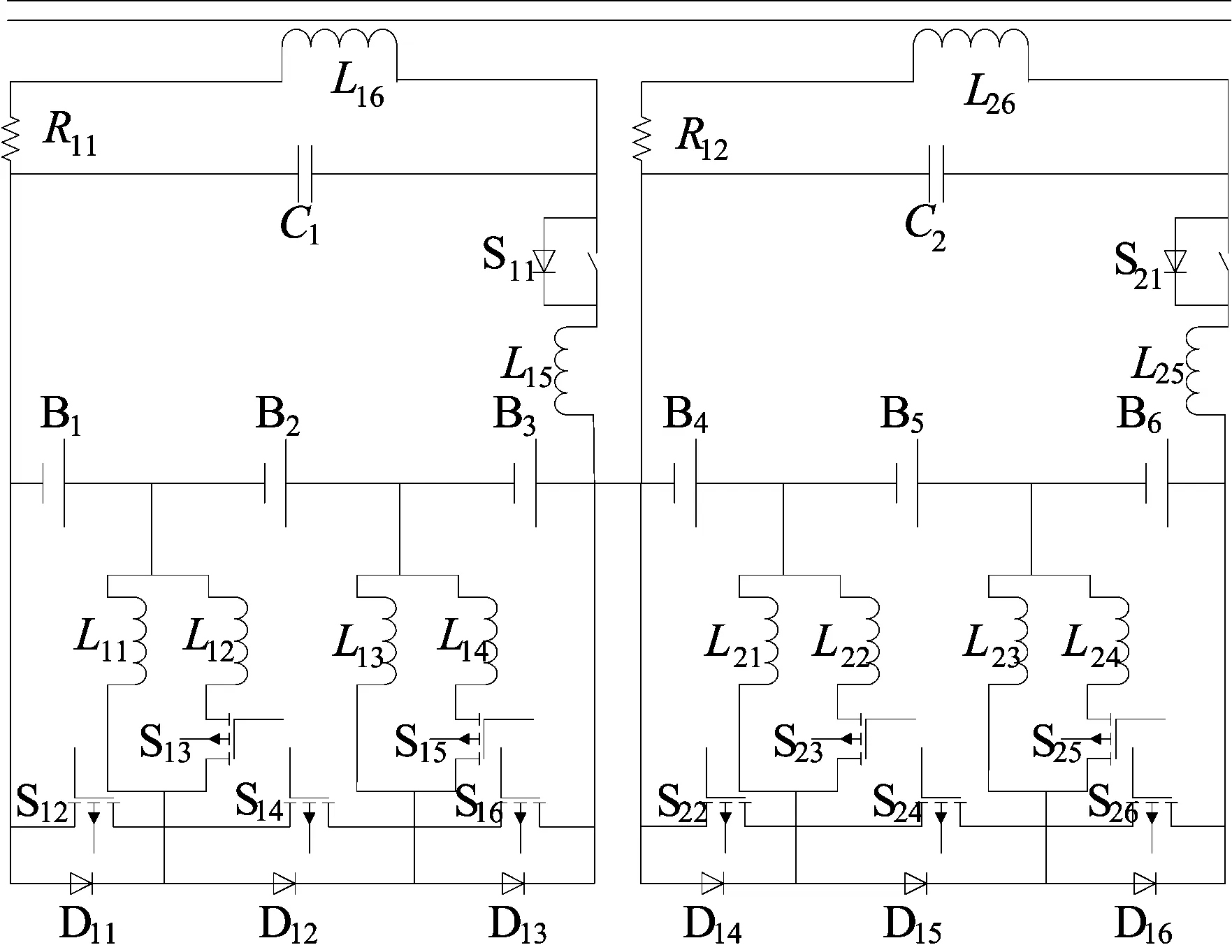
图3 新型均衡拓扑结构
整个均衡过程包括充电均衡与放电均衡,充电均衡为电压低的电池补充能量,放电均衡对电压高的电池进行能量抽取。本质上都是能量转移,下面主要说明混合拓扑的能量转移过程。
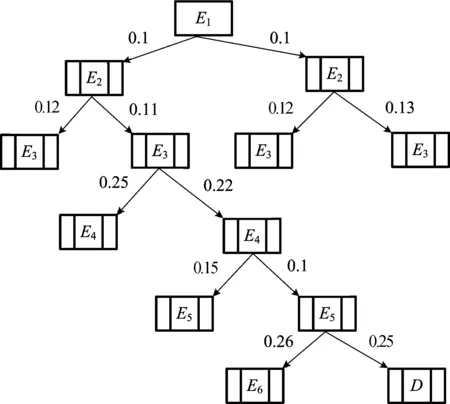
2.1 组间均衡
组间采用集中式均衡拓扑结构,其中电容与电感构成LC振荡回路,既可以保证磁芯的可靠复位,也可以实现软开关来降低开关功耗。该电路可以实现任意两组间的能量传递,因此均衡效率较高。具体过程为:设组1电压为V11,组2电压为V22;若V11 (1) 电流i为: 代入(1)式可得: 由于开关采用脉冲控制,在电压差距较大时,能量不可能一次转移完成,需要转移n次。理论上分析,由于采用了同轴多绕组变压器均衡拓扑结构,使得各组间的电压得到完全均衡。但由于制造工艺的差异,难以保持真正的一致,因此转移能量会略小于E。 2.2 组内均衡 组内均衡采用分布式均衡拓扑结构,每节单体电池都有属于自己的均衡模块,以3节电池为1组,可以实现任意两节电池间的均衡。可以同时均衡的单体电池数达到最大。两节电池间采用双电感模式,如图3所示,其中L12≪L11。 若V1最大,则打开S12,电感L11储能;关断S12,L11通过二极管对电池2与电池3进行续流充电,电池2获得大部分能量。此时有: (2) (3) (4) 其中,D为电路中开关的占空比;T为电路中开关的周期;V1、V2、V3分别为电池1、电池2、电池3的电压;ΔV为电感两端的电压。 若V2最大,则有如下3种情况。 (1)V1、V3均较小,打开S14,电感L11、L13储能;关断S14,电感L11向电池2充电,电感L13向电池3充电。此时有: (5) (6) 由(5)式、(6)式可以看出,与单节电池的均衡相比,同时均衡两节电池,均衡电流会相对减少。 (2)V1最小,V3与V2差距很小,则打开S14与S15,由于L14与L13相比很小,L13被短路,此时大部分能量都储存在L11中,关断S14与S15,电感L11向电池1充电,这样就避免了L11与L13同时储能时不必要的能量损耗。 (7) 由于L14≪L11,L11可忽略不计,则有: (8) (3)V3最小,V1与V2差距很小,与第2种情况类似,此时电池2主要向电池3充电。但此时电流由于后续电池的影响会略有减少,均衡电流为: (9) 若V3最大,则打开S14,电感L13储能,关断S16,L13通过二极管对电池2与电池1进行续流充电,电池2获得大部分能量。此时情况与第2种情况类似。但此时没有后续电流影响,均衡电流为: (10) (11) 以上为混合均衡拓扑结构的几种均衡方式,该新型拓扑结合了分布式均衡与集中式均衡的优缺点,从硬件结构上使得能量传输路径缩短,均衡效率得以大大提高,可以同时均衡的单体电池数达到总电池数的1/3以上,并且模块化强,易于扩展;主要缺点是虽然采用同轴多绕组变压器,但当电池数量很大时,同轴变压器设计将变得困难且不易维修。此外组与组间均衡电流存在细微的相互干扰。 在均衡拓扑结构一定的条件下,制定出一套合适的均衡控制策略是非常必要的。目前均衡控制策略种类繁多[9-10],总体分为2类:① 基于电压的均衡方法;② 基于容量的均衡方法。 其中基于容量的均衡方法是基于准确预估单体电池的荷电状态(state of charge,SOC),若SOC的准确性得不到保证,均衡的可靠性会大大降低。因此当前实际应用的控制策略多数采用基于电压的均衡方法。该均衡方法以实时测得的电池端电压为依据进行均衡。但经过实际测试发现锂离子电池具有电压自恢复性,即电池在终止充电或放电后,电压会有一个恢复过程。恢复程度与电池本身性能有关。电池性能较好则恢复程度较小,电池性能较差则恢复程度较大[11-13]。因此,本文的控制策略首先设置一定的过均衡度,保证均衡的可靠性,如图4所示。过均衡度通过多次充放电实验测得电池使用的不同时期的恢复程度,以此作为过均衡度的数据支撑。 图4 过均衡度的设置 判断一个控制策略的好坏主要取决于能量转移的多少与能量转移速度。由于均衡拓扑结构做出了改进设计,从硬件上保证了较高的均衡速度。因此本文提出一种最优能量转移的控制策略。下面将具体说明。 由于均衡拓扑结构采用变压器作为能量转移的媒介,理论上分析不存在均衡能量损耗。但在实际使用过程中,由于变压器直流阻抗与电路阻抗的存在,能量转移过程中会产生能量损耗。转移能量越多,则损耗越大。本文能量转换的最优方案指在满足均衡目的的前提下,找寻出转移能量最少的路径以降低均衡损耗。基于此,选取深度优先搜索算法用来搜索最优转移路径[14-16]。深度优先搜索算法属于盲目搜索的一种,会穷举出所有路径,以找到最佳路径。这种搜索算法不会舍弃节点,因此杜绝了舍弃掉最优路径的可能性,但该算法具有盲目性,效率低下。由于均衡拓扑结构采用分组结构,组内均衡时路径数会大大减少,使得该算法能够符合最优能量转移的要求,在较短的时间内穷举出所有路径。 该算法满足一个估计函数[17],即 f(n)=g(n)+h(n), 其中,f(n)为每个可能搜索路径的估值,由2个部分组成;g(n)为从起始搜索点到当前搜索点的代价;h(n)为深度优先搜索中最重要的一环,即当前节点到目标节点的估值。将之应用于最优能量转移需要加一些约束条件,以便找到能量损耗最少的路径。均衡策略搜索示意图如图5所示。约束条件为: (1) 图5中每个节点的后继节点是有限的,即在未达到均衡目标时,总有可供选择的转移路径。 (2) 图5中从一个节点到另一个节点的搜索代价都大于某个正数,即每条能量转移路径都存在能量损耗。 (3) 对于图5中所有节点n都有h(n)≤h*(n)(h*(n)为实际选择路径的代价值),即所选均衡路径不大于其他任意一条均衡路径。 图5 均衡策略 综上所述,控制策略具体过程为: (1) 依据历史数据确定此时的过均衡度。 (2) 考虑电感的直流阻抗及电路阻抗,建立均衡电路阻抗模型。 (3) 检测电池端电压,找出需均衡的单体电池。 (4) 以阻抗模型为基础,采用深度优先搜索算法估算出每条路径所需消耗的能量,找出最优能量转移路径,完成均衡。 本文采用Matlab/SimPowerSystem 工具箱进行仿真实验。 首先证明本文改进的均衡拓扑结构的正确性。取2组电池实验,电池数每组为9颗,所取电池为磷酸铁锂电池,电压范围为2.5~4.0 V。将2组电池从同一起点进行综合放电实验,一组加入所设计的混合均衡拓扑电路,另一组自由放电。 实验结果如图6所示。 图6 混合拓扑结构的正确性实验 从图6可以看出,在同等放电条件下,放电完毕后,没有均衡的电池组剩余较高电量,放电不完全,采用混合均衡拓扑的电池组能够更大限度地放出能量,提升电池组性能。 由于结构进行了改进,混合拓扑结构在均衡效率方面有较大的提升。以集中式均衡为例,将集中式均衡拓扑与混合拓扑进行仿真对比。选取9节磷酸铁锂电池,分为3组,其中3组中有1节电池电压较低,1节电池电压较高,以此为基础进行均衡实验。同等条件均衡对比实验结果如图7所示。 图7 同等条件均衡对比实验 图7表示2节电池分别在同等初始条件下均衡电路不同时,从初始条件到达均衡状态的过程。从图7可以看出,电池电压较高时,从均衡起始至结束混合拓扑均具有较高的均衡速度,因此将率先到达均衡状态,节省均衡时间;电池电压较低时,由于集中式拓扑有整组电池向单体电池充电,电流较大,均衡起始时均衡速度较快,但到后期还是会落后于混合拓扑。 综上可知,在均衡速度方面,混合与拓扑具有很大的优势[18]。 最后对均衡控制策略进行对比分析,采用同上的9节单体电池为例。 设定好电池组的不均衡状态,将传统的电压高低排序依次均衡的方法与本文基于能量转移的最优控制策略进行对比实验。其中均衡能量损耗满足: (12) 其中,RI为组内线路等效电阻;RC为电感阻抗。 根据实验结果进行分析计算,得出2种均衡策略的能量损耗,如图8所示。 从图8可以看出,基于能量转移的最优控制策略在均衡能量损耗方面明显优于传统的均衡策略。 图8 均衡能量损耗对比分析 本文结合分布式均衡拓扑与集中式均衡拓扑的优缺点,设计了一种混合均衡拓扑。该结构中组内与组间均衡可以同时进行,并且各组之间也可同时均衡,以3节电池为1组,同一时间可同时均衡的单体电池数可达电池组的1/3以上,且易于模块化,适用性增强。本文还采用设置过均衡度的方法,结合深度最优搜索算法,设计出了符合新型拓扑的最优能量转移均衡策略。经过试验分析,该策略可以有效降低电池组的不一致性,提升电池组的整体性能,增加电池组的使用寿命,提高能量利用率。今后将对新型均衡拓扑的不足之处继续进行改进,对控制策略的可靠性与稳定性进行优化。 [1] 韩江洪,王龙飞,刘征宇,等.基于剩余容量的锂离子电池组均衡策略 [J].电子测量与仪器学报,2014,28(10):1047-1052. [2] 王林霞,王涌,郑荣鹏.锂离子电芯一致性对电池组影响的研究[J].电源技术,2012,36(9):1282-1284. [3] 熊永华,杨艳,李浩,等.基于SOC的锂动力电池多层双向自均衡方法[J].电子学报,2014,40(4):766-773. [4] LI S Q,MI C,ZHANG M Y.A high efficiency low cost direct battery balancing circuit using a multi-winding transformer with reduced switch count [C]//2012 Twenty-Seventh Annual IEEE Applied Power Electronics.Orlando,Florida:IEEE,2012:2128-2133. [5] WANG J Y,SUN Z C,WEI X Z,et al.Lifespan uniformity for the battery pack in the automotive application[J].Automotive Safety and Energy,2011,2(3):223-228. [6] LI C P,XIA B Z,LI X L,et al.A new type battery equalization circuit of electric vehicle[J].Advanced Materials Research,2012,535/536/537:495-499. [7] KUHN B T,PITEL G E,KREIN P T.Electrical properties and equalization of lithium-ion cells in automotive applications[C]//2005 IEEE Conference on Vehicle Power and Propulsion.Standford,California:IEEE Xplore,2005:55-59. [8] 宋海飞,曹亚,王艳.一种新颖的动力电池均衡方法研究[J].电力电子技术,2013,38(5):423-427. [9] 黄勤,严贺彪,凌睿.串联锂电池组无损均衡管理方案设计与实现[J].计算机工程,2012,37(12):226-229. [10] HSIEH Y C,WU J L,CHEN X H.Class-E-based charge equalization circuit for battery cells[J].IET Power Electronics,2012,5(7):978-983. [11] 张晓,姜久春,张维戈.动力电池参数分析及参数检测的实现[J].电测与仪表,2011,48(4):18-22. [12] WANG H,SHAO D G,XU L.Research on a new type of lithium battery string equalization and management system[J].Advanced Materials Research,2011,383/384/385/386/387/388/389/390:1470-1476. [13] CHEN M,ZHANG Z,FENG Z,et al.An improved control strategy for the charge equalization of lithium ion battery[C]//Applied Power Electronics Conference and Exposition.Singapore:IEEE Xplore,2009:186-189. [14] LIN P C,LEE C H,HUANG Y S,et al.Battery energy balance circuit and battery charging bypass circuit:US7049791[P].2006-05-23. [15] HANDA A,STUART T A.A selective equalizer for Ni-MH batteries[J].Journal Power Sources,2004,138(1/2):327-339. [16] LING R,DONG Y,YAN H,et al.Fuzzy-PI control battery equalization for series connected lithium-ion battery strings[C]// Power Electronics and Motion Control Conference.Harbin:IEEE,2012:2631-2635. [17] 李平,何明华.一种电池组均衡电路及其控制策略设计[J].电源技术,2011,87(10):1204-1214. [18] 朱东,曾祥兵,任海娟.混合动力汽车用镍氢电池性能研究[J].合肥工业大学学报(自然科学版),2011,34(12):1792-1794,1845. (责任编辑 胡亚敏) A hybrid topology based on optimal energy transfer path YAN Gang1,2, ZHANG Li3,4, JING Junfeng3, LIU Zhengyu3,4 (1.School of Management, Hefei University of Technology, Hefei 230009, China; 2.Jianghuai Automobile Co., Ltd., Hefei 230091, China; 3.School of Mechanical Engineering, Hefei University of Technology, Hefei 230009, China; 4.Engineering Research Center of Safety Critical Industrial Measurement and Control Technology of Ministry of Education, Hefei 230009, China) Power battery equalization is an important technology in the application of electric vehicles. At present, the balance degree of battery pack is the only control criterion in the majority of equalizer circuit and control strategies. The energy utilization rate is ignored. In this paper, a balanced circuit combining the distributed-load balancing and the central-load balancing is designed to improve the balancing speed to a large extent. An equilibrium control strategy based on transferring least energy is also put forward. The results of simulation experiment show that the equalization circuit is correct. The control strategy can improve the energy utilization and reduce the loss. This method can be used in practical applications. balancing topology; balancing speed; balancing strategy; energy dissipation 2015-09-29; 2015-12-21 国家国际科技合作专项资助项目(2012DFB10060) 严 刚(1963-),男,安徽含山人,合肥工业大学博士生,江淮汽车股份有限公司教授级高工; 张 利(1955-),女,安徽蚌埠人,合肥工业大学教授,硕士生导师. 10.3969/j.issn.1003-5060.2017.04.001 TN86 A 1003-5060(2017)04-0433-06

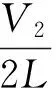
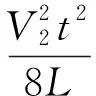
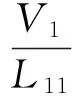
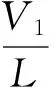
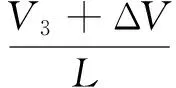
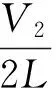
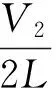
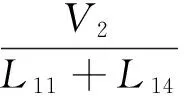
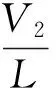
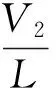
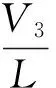
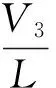
3 均衡策略

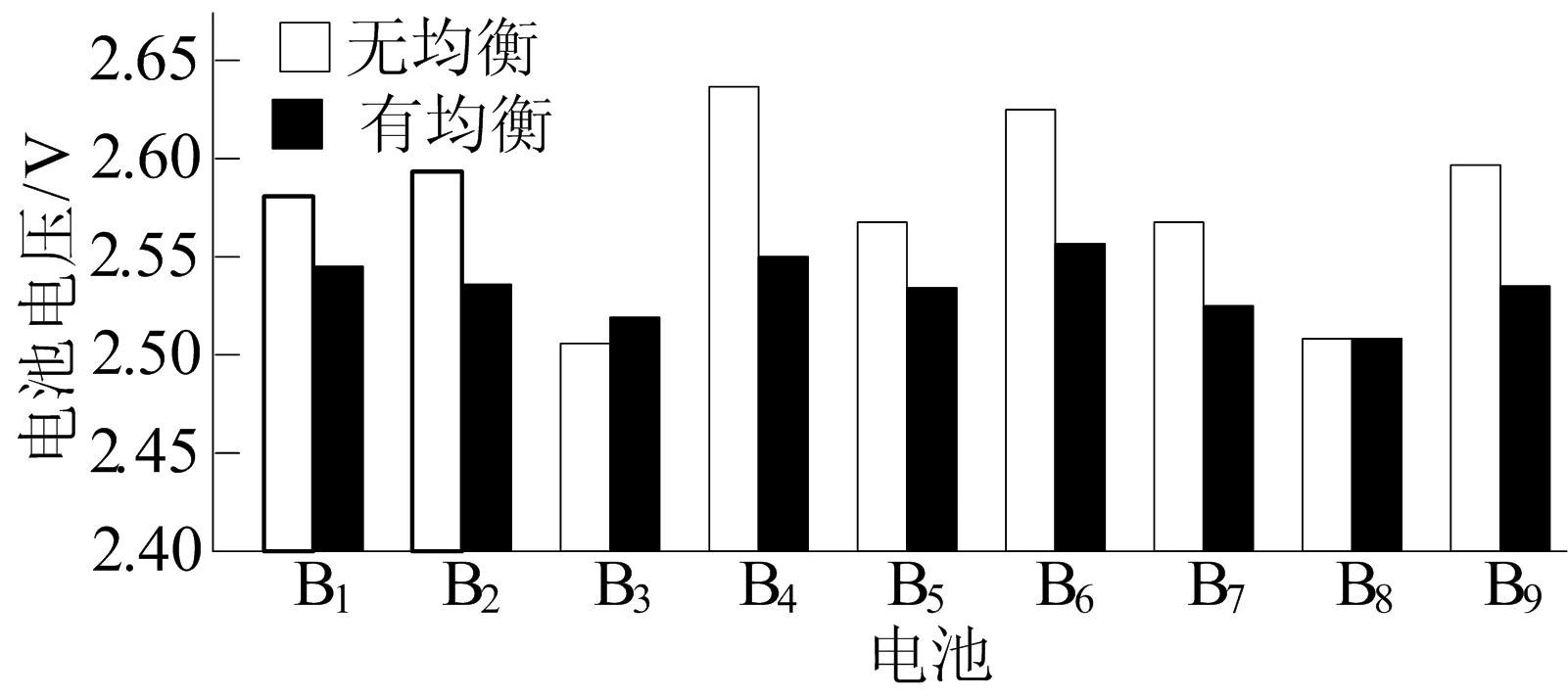
4 实验分析

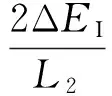


5 结 论

