量子计算机
量子计算机
·编者按·
量子计算机,是一种遵循量子力学规律进行高速数学和逻辑运算、存储及处理量子信息的物理装置。量子计算用来存储数据的载体是量子比特,它使用量子算法来进行数据操作。20世纪80年代,量子计算作为一个新的学科方向诞生,源于量子力学和计算机科学与技术的结合。虽然量子计算最初是为了解决物理问题提出的,但随着量子计算的理论和实验技术的发展,量子计算和量子计算机受到了计算机科学与技术领域的广泛关注。量子计算理论表明,量子计算机具有比电子计算机更强的计算能力。目前,量子计算机实现面临着退相干带来的一系列困难,以及一些技术上的问题。据悉,中国科学家已经能够对单粒子和量子态进行调控,开始从“观测时代”走向“调控时代”,量子计算机的实现值得期待。
本专题得到郭光灿院士(中国科学技术大学)、李传锋教授(中国科学技术大学)、张焕国教授(武汉大学)、张洪涛教授(湖北工业大学)的大力支持。
·热点数据排行·
截至2017年 4月 17日,中国知网(CNKI)和Web of Science(WOS)的数据报告显示,以“量子计算机”为词条可以检索到的期刊文献分别为1572、 3393条,本专题将相关数据按照:研究机构发文数、作者发文数、期刊发文数、被引用频次进行排行,结果如下。
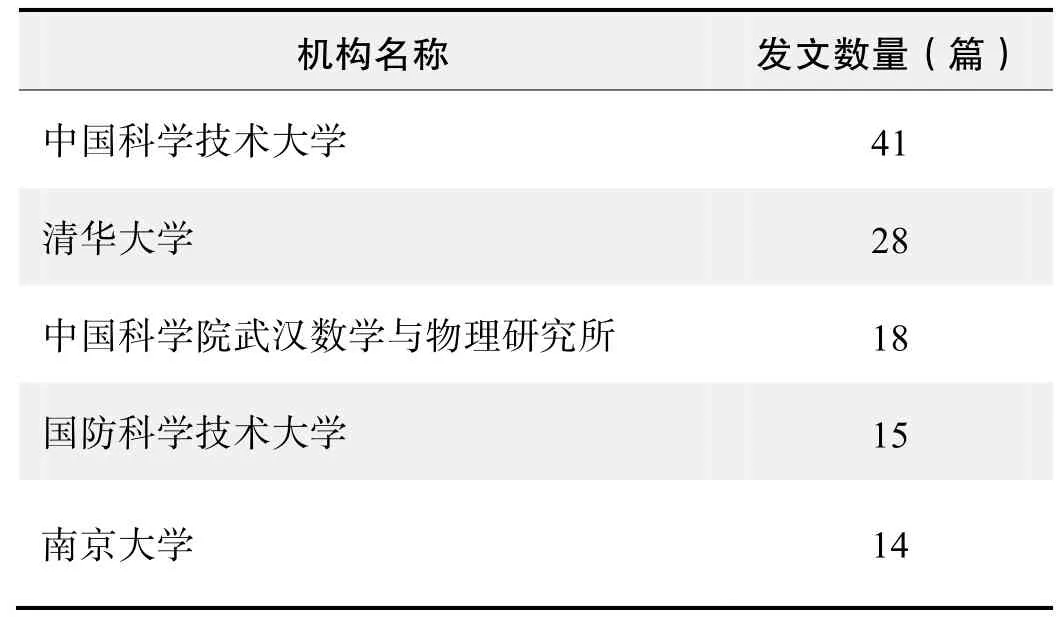
研究机构发文数量排名(CNKI)
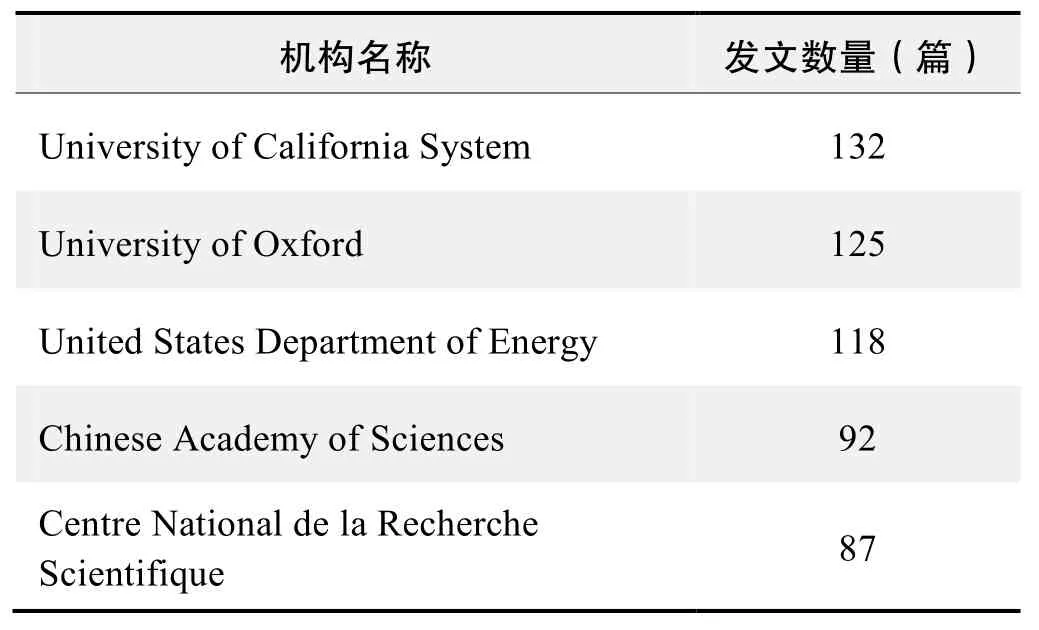
研究机构发文数量排名(WOS)

作者发文数量排名(CNKI)

作者发文数量排名(WOS)

作者发文数量排名(CNKI)(续表)

作者发文数量排名(WOS)(续表)
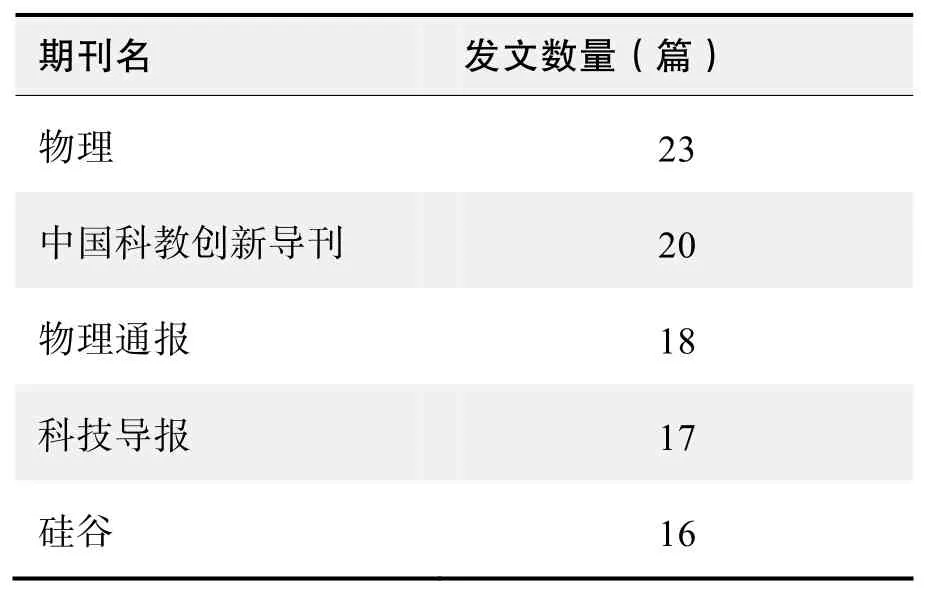
期刊发文数量排名(CNKI)

期刊发文数量排名(WOS)
根据中国知网(CNKI)数据报告,以“量子计算机”等为词条可以检索到的高被引论文排行结果如下。

国内数据库高被引论文排行
根据Web of Science统计数据,以“量子计算机”为词条可以检索到的高被引论文排行结果如下。
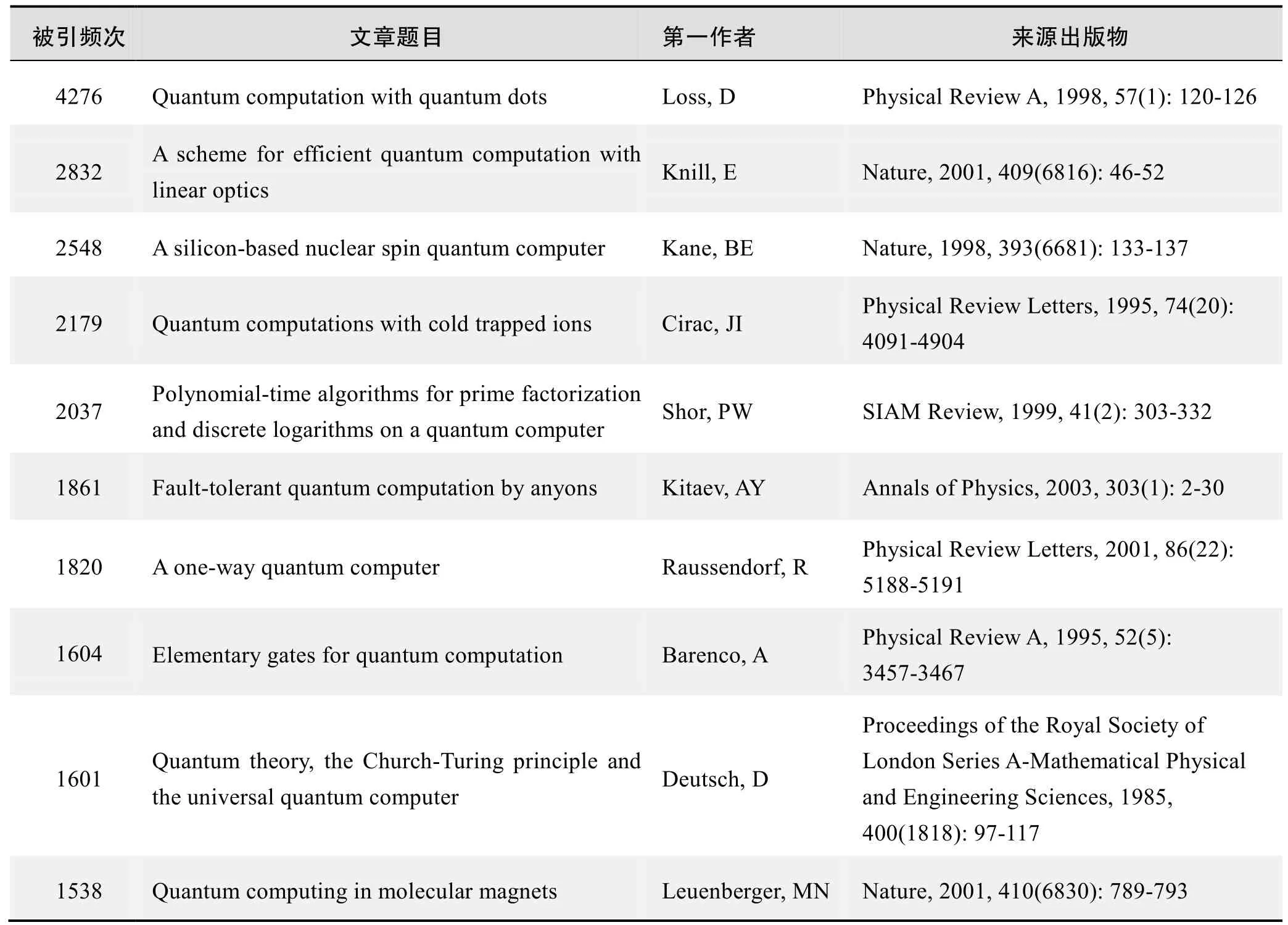
国外数据库高被引论文排行
·经典文献推荐·
基于Web of Science检索结果,利用Histcite软件选取 LCS(Local Citation Score,本地引用次数)TOP 30文献作为节点进行分析,得到本领域推荐的经典文献如下。
Abstract: Over the past several decades, quantum information science has emerged to seek answers to the question: can we gain some advantage by storing, transmitting and processing information encoded in systems that exhibit unique quantum properties? Today it is understood that the answer is yes, and many research groups around the world are working towards the highly ambitious technological goal of building a quantum computer, which would dramatically improve computational power for particular tasks. A number of physical systems, spanning much of modern physics, are being developed for quantum computation. However, it remains unclear which technology, if any, will ultimately prove successful. Here we describe the latest developments for each of the leading approaches and explain the major challenges for the future.
来源出版物:Nature, 2010, 464, 45-53
Quantum theory, the Church-Turing principle and the universal quantum computer
Deutsch, D
It is argued that underlying the Church-Turing hypothesis there is an implicit physical assertion. Here, this assertion is presented explicitly as a physical principle: ‘every finitely realizable physical system can be perfectly simulated by a universal model computing machine operating by finite means’. Classical physics and the universal Turing machine, because the former is continuous and the latter discrete, do not obey the principle, at least in the strong form above. A class of model computing machines that is the quantum generalization of the class of Turing machines is described, and it is shown that quantum theory and the‘universal quantum computer’ are compatible with the principle. Computing machines resembling the universal quantum computer could, in principle, be built and would have many remarkable properties not reproducible by any Turing machine. These do not include the computation of non-recursive functions, but they do include ‘quantum parallelism’, a method by which certain probabilistic tasks can be performed faster by a universal quantum computer than by any classical restriction of it. The intuitive explanation of these properties places an intolerable strain on all interpretations of quantum theory other than Everett’s. Some of the numerous connections between the quantum theory of computation and the rest of physics are explored. Quantum complexity theory allows a physically more reasonable definition of the ‘complexity’ or‘knowledge’ in a physical system than does classical complexity theory.
来源出版物:Proceedings of the Royal Society of London Series A-Mathematical Physical and Engineering Sciences, 1985, 400(1818): 97-117
Rapid solution of problems by quantum computation
Deutsch, D; Jozsa, R
Abstract: A class of problems is described which can be solved more efficiently by quantum computation than by any classical or stochastic method. The quantum computation solves the problem with certainty in exponentially less time than any classical deterministic computation.
来源出版物:Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. The Royal Society, 1992, 439(1907): 553-558
Elementary gates for quantum computation
Barenco, A; Bennett, CH; Cleve, R; et al.
Abstract: We show that a set of gates that consists of all one-bit quantum gates [U(2)] and the two-bit exclusive-OR gate [that maps Boolean values (x,y) to (x,x⊕y)] is universal in the sense that all unitary operations on arbitrarily many bits n [U(2n)] can be expressed as compositions of these gates. We investigate the number of the above gates required to implement other gates, such as generalized Deutsch-Toffoli gates, that apply a specific U(2) transformation to one input bit if and only if the logical and of all remaining input bits is satisfied. These gates play a central role in many proposed constructions of quantum computational networks. We derive upper and lower bounds on the exact number of elementary gates required to build up a variety of two- and three-bit quantum gates, the asymptotic number required for n-bit Deutsch-Toffoli gates, and make some observations about the number required for arbitrary n-bit unitary operations.
来源出版物:Physical Review A, 1995, 52(5): 3457-3467
Quantum computation and Shor’s factoring algorithm
Ekert, A; Jozsa, R
Abstract: Current technology is beginning to allow us to manipulate rather than just observe individual quantum phenomena. This opens up the possibility of exploiting quantum effects to perform computations beyond the scope of any classical computer. Recently Peter Shor discovered an efficient algorithm for factoring whole numbers, which uses characteristically quantum effects. The algorithm illustrates the potential power of quantum computation, as there is no known efficient classical method for solving this problem. The authors give an exposition of Shor’s algorithm together with an introduction to quantum computation and complexity theory. They discuss experiments that may contribute to its practical implementation.
来源出版物:Reviews of Modern Physics, 1996, 68 (3): 733-753
Quantum computers
Ladd, TD; Jelezko, F; Laflamme, R; et al.
典
1 2 3 4 5文章题目Quantum theory, the Church-Turing principle and the universal quantum computer Rapid solution of problems by quantum computation Elementary gates for quantum computation Quantum computation and Shor's factoring algorithm Quantum computers第一作者Deutsch, D Deutsch, D Barenco, A Ekert, A Ladd, TD来源出版物Proceedings of the Royal Society of London Series A-Mathematical Physical and Engineering Sciences, 1985, 400(1818): 97-117 Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. The Royal Society, 1992, 439(1907): 553-558 Physical Review A, 1995, 52(5): 3457-3467 Reviews of Modern Physics, 1996, 68 (3): 733-753 Nature, 2010, 464, 45-53

