基于Contourlet变换和交替方向法的压缩感知图像重构算法
邹健
(长江大学信息与数学学院,湖北 荆州 434023)
基于Contourlet变换和交替方向法的压缩感知图像重构算法
邹健
(长江大学信息与数学学院,湖北 荆州 434023)
在传统的基于压缩感知的图像重构中,小波变换往往用来将图像稀疏表示,但小波变换并不能很好的表现图像的轮廓和纹理等细节信息。提出了一种基于Contourlet变换和交替方向法的压缩感知图像重构算法:首先利用Contourlet变换将图像稀疏表示,然后利用交替方向法重构原始图像。与基于小波变换的方法相比,该方法不仅可以显示更多的图像的边缘和轮廓信息,在重构精度上也占优。数值试验也验证了新算法的有效性。
压缩感知;图像重构;Contourlet变换;交替方向法
压缩感知是一种新型的信号采样和处理的理论框架[1~3]。利用信号在特定域上的稀疏性,压缩感知可以从少量测量值中重构信号,且所需测量值远低于奈奎斯特采样定理的要求。基于以上优点,压缩感知近年来引起了广泛的关注,在各个领域都有广泛的应用,图像重构正是其中一个重要的应用领域[4~6]。
在压缩感知模型中,要求重构信号本身是稀疏的,或者在某个变换基下具有稀疏表示。在以往的压缩感知模型中,常采用小波变换作为稀疏变换基,图像经过小波变换后的小波系数是稀疏的[2, 7]。但是由于小波变换的各向同性,导致小波变化的方向选择性差,很难充分和准确地捕捉到图像的边缘和轮廓信息,而图像的边缘和轮廓是自然图像的主要特性。Contourlet变换是在继承小波多尺度分析思想的基础上的一种新的非自适应的方向多尺度分析方法。Contourlet变换能在任意尺度上实现任意方向的分解,擅长描述图像中的轮廓和方向性纹理信息,很好的弥补了小波变换的不足。此外,Contourlet变换直接在分离领域中实现,有较低的计算复杂度[8, 9]。
压缩感知的另外一个关键问题就是重构算法。一些传统的优化方法,如内点法等,需要计算压缩感知矩阵的二阶导数等信息[10]。但在实际应用中,特别是一些图像和高维数据处理问题,压缩感知矩阵的维数往往相当大,采用这些方法往往需要很长的重构时间,甚至有时计算机会报告内存溢出。交替方向法只利用目标函数的一阶导数信息,算法中只涉及到矩阵-向量相乘等低复杂度的计算,适合大规模问题的求解[11, 12]。为此,笔者提出一种基于Contourlet变换和交替方向法的压缩感知图像重构算法。
1 基于Contourlet变换的压缩感知模型
压缩感知的基本问题是从欠定线性测量y=Φx中重构信号x,其中x∈Rn,Φ∈Rm×n(m≪n)。该欠定线性方程组有无穷多解。但压缩感知理论指出,如果x是稀疏的,即x中非零元数目远小于其维数,则可通过求解如下优化问题重构x:
(1)
式中,‖x‖0为向量x中非零数目。
式(1)为NP-难的非凸优化问题[13],不易求解,可以将其转化为如下优化问题:
(2)
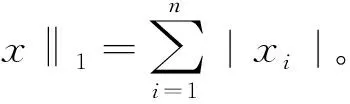
式(1)和式(2)中都假设x是稀疏的,但大多数实际情况中,信号本身不是稀疏的,但在某种变换下具有稀疏表示,即:
x=Ψθ
式中,x是原始信号;Ψ为稀疏变换矩阵;θ为x在Ψ下的表示系数。x本身并不稀疏,但在是稀疏变换矩阵Ψ下的表示系数θ是稀疏的。在该情况下,压缩感知模型即变为:
y=Φθ=ΦΨ*x=Ax(Ψ*为Ψ的逆矩阵)
此时,要想重构原始信号x,则应求解如下优化问题:
(3)
2 基于交替方向法的压缩感知重构算法
交替方向法是一种求解大规模稀疏优化问题的有效算法,其通过构造增广拉格朗日函数,将原问题分解为多个低维子问题进行求解。
令f(x):Rm→R和g(y):Rn→R为凸函数,A∈Rp×m,B∈Rp×n,b∈Rp。对最优化问题:

(4)
其中变量x,y在目标函数中分离,在约束中耦合。
式(4)的增广拉格朗日函数为:

(5)
其中,λ∈Rp为拉格朗日乘子;β>0为罚参数。
经典的拉格朗日方法迭代为给定λk∈Rp:
(6)
λk+1=λk-γβ(Axk+1+Byk+1-b)
(7)
其中,γ∈(0,2)保证迭代的收敛性。
式(6)是一个关于(x,y)的一个精确联合的极小化问题,不易求解。交替方向法将目标函数的变量分离并通过2个简单的子问题代替上面联合的极小化。交替方向法基本迭代步骤如下:
(8)
(9)
这里笔者将利用交替方向法求解优化问题(3)。首先引入一个对偶变量z,将式(3)转化为:
(10)
式(10)的增广拉格朗日函数为:
(11)
如果固定x=xk,λ=λk, 即:

(12)
则f(xk,z)仅是关于z的函数,此时式(11)等价于:
(13)
对式(13), 令:
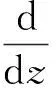
可得:

则式(13)的最优值z可表示为:
(14)
其中,PBδ(·)为函数在球面Bδ:{z:‖z‖2≤δ}上的投影。
固定z=zk+1,λ=λk,即:

(15)
此时目标函数f(x,zk+1)仅与x有关,式(11)等价于:
(16)
其中,式(15)可化简为:

(17)
令:

将h(x)在xk处泰勒展开,得:
(18)

此时式(16)可表示成:
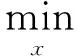
(19)
进一步化简可得:
(20)
问题(20)有封闭解,其解可用收缩算子(软阈值)来表示如下:
(21)
乘子λ更新步骤如下:
λk+1=λk-γβ(Axk+1+zk+1-y)
(22)
其中,γ>0为常数。
综上所述,求解式(3)的迭代算法可以表示如下:
输入:A,y,r0,x0,λ0,β>0,γ>0,Γ>0。
输出:x
while”不满足停止准则”do
λk+1=λk-γβ(Axk+1+zk+1-y);
endwhile
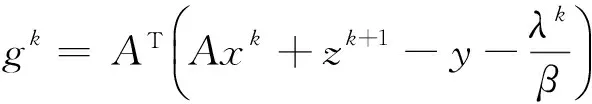
3 仿真试验
使用标准测试图片lena,将测试图片分别通过小波变换和Contourlet变换进行稀疏表示,然后利用笔者提出的算法进行图像重构。重构性能用峰值信噪比 (peaksignaltonoiseratio,PSNR)来度量,PSNR的定义如下:
(23)


试验结果如图1所示,为更直观的展示重构效果,选取原始图像中白色框中的局部图像进行放大展示,从试验结果可以看出,与小波变换相比,Contourlet变换后重构的图片边缘和轮廓更加清晰。而小波变换重构和Contourlet变换重构图像的PSNR分别为25.60dB和27.40dB,也验证了Contourlet变换比小波变换的重构精度更高。

图1 不同方法重构图像对比
4 结语
笔者提出了一种新的压缩感知图像重构方法,新方法利用Contourlet变换作为稀疏变换基,利用交替方向法重构稀疏信号。新方法具有较低的计算复杂度,适用于大规模图像重构,仿真试验结果也验证了新方法的有效性。在今后工作中,将考查更多的多尺度稀疏变换基对图像重构结果的影响。
[1]CandesEJ,WakinMB.Anintroductiontocompressivesampling[J].IEEESignalProcessingMagazine, 2008, 25(2): 21~30.
[2]ZhaoD,DuHQ,HanY,etal.CompressedSensingMRImageReconstructionExploitingTGVandWaveletSparsity[J].Computational&MathematicalMethodsinMedicine, 2014: 958671.
[3]DonohoDL.Compressedsensing[J].IEEETransactionsonInformationTheory, 2006, 52(4): 1289~306.
[4]ShenYF,LiJT,ZhuZM,etal.Imagereconstructionalgorithmfromcompressedsensingmeasurementsbydictionarylearning[J].Neurocomputing, 2015, 151(3): 1153~1162.
[5]WrightJ,MaY,MairalJ,etal.Sparserepresentationforcomputervisionandpatternrecognition[J].ProceedingsoftheIEEE, 2010, 98(6): 1031~1044.
[6]EladM,FigueiredoMAT,MaY.Ontheroleofsparseandredundantrepresentationsinimageprocessing[J].ProceedingsoftheIEEE, 2010, 98(6): 972~982.
[7]ChenC,HuangJZ.ExploitingthewaveletstructureincompressedsensingMRI[J].MagneticResonanceImaging, 2014, 32(10): 1377~1389.
[8]DoMN,VetterliM.Thecontourlettransform:anefficientdirectionalmultiresolutionimagerepresentation[J].IEEETransactionsonImageProcessing, 2005, 14(12): 2091~2106.
[9]QuXB,ZhangWR,GuoD,etal.IterativethresholdingcompressedsensingMRIbasedoncontourlettransform[J].InverseProblemsinScienceandEngineering, 2010, 18(6): 737~758.
[10]KimSJ,KohK,LustigM,etal.AnInterior-PointmethodforLarge-Scalel1-Regularizedleastsquares[J].IEEEJournalofSelectedTopicsinSignalProcessing, 2007, 1(4): 606~617.
[11]BoydS,ParikhN,ChuE,etal.Distributedoptimizationandstatisticallearningviathealternatingdirectionmethodofmultipliers[J].Foundations&TrendsinMachineLearning, 2011,3(1): 1~122.
[12]YangJ,ZhangY.Alternatingdirectionalgorithmsfor$ell_1$~Problemsincompressivesensing[J].SiamJournalonScientificComputing, 2009, 33(1): 250~278.
[13]BrucksteinAM,DonohoDL,EladM.Fromsparsesolutionsofsystemsofequationstosparsemodelingofsignalsandimages[J].SiamReview, 2009, 51(1): 34~81.
[编辑] 洪云飞
2016-12-16
国家自然科学基金项目(61503047)。
邹健(1983-),男,博士,副教授,现主要从事最优化方法及其在信号处理中的应用方面的教学与研究工作,zoujian@yangtzeu.edu.cn。
TP391.4
A
1673-1409(2017)05-0001-05
[引著格式]邹健.基于Contourlet变换和交替方向法的压缩感知图像重构算法[J].长江大学学报(自科版),2017,14(5):1~5.

