基于扰动观测器的伺服系统扰动抑制研究

季 画，王 爽，黄苏融，石 坚

(1.上海大学,上海200072;2.山东理工大学,淄博255091)

0 引 言

随着伺服系统在轨道交通、风力发电、航空航天、电动汽车等行业的广泛应用,对伺服系统的性能要求越来越高。实际系统中,外界因素如负载变化引起的转矩波动,信号获取的测量噪声和量化误差,使得系统动态过程的控制性能变差。为此,要获得伺服系统高性能控制,要求系统具有较快的动态响应速度、较高的稳态控制精度,且对模型参数变化和负载扰动具有较强的抑制能力。

国内外学者提出了多种扰动抑制的方案,如加速度控制[1-2]、状态反馈控制[3-5]、扰动观测器[6-13]以及滑模变结构控制[14]、自适应控制[15]等。

加速度反馈的引入提高了系统的抗扰能力,但却减缓了控制系统的速度响应[1-2]。同时,加速度信号的获取困难,受限于加速度传感器过高的成本或位置传感器信号二次微分所引入的大量的噪声干扰。状态观测器能够估计出电机的瞬时状态,将估计到的状态变量反馈到输入端构成状态反馈控制,可以有效抑制扰动[3-5]。状态观测器的变量估计具有较好的实时性,但是对于高阶状态方程,难以得到准确的参数,同时抗干扰能力不佳,在噪声环境中,状态变量的估计可能失效。

扰动观测器是估计和补偿负载扰动的一种有效方式。文献[6]提出采用扰动观测器观测和补偿施加于整个系统的扰动转矩。由于扰动观测器不需要复杂的参数辨识,结构简单,易于实现,此方法一经提出就引起许多学者的关注和研究,并将其应用于伺服系统中以提高系统的抗干扰能力[7-8]。扰动观测器的性能取决于所含低通滤波器的设计,许多文献对滤波器进行了详细的分析和设计。文献[9]提出了n阶滤波器及其简单的参数设计。文献[10]分析了高阶扰动观测器的实现。随着扰动观测器阶次的提高,灵敏度变低而响应速度变高。然而阶次的提高对系统的鲁棒稳定性产生不利的影响。

低通滤波器的截止频率决定着扰动观测器扰动抑制的性能。因此,设置较高的滤波器截止频率显得非常重要。然而,截止频率受限于系统的采样周期和观测噪声[11]。较高的截止频率在扰动转矩估计时易受所包含的观测噪声的影响。文献[12]分析了扰动抑制性能和测量噪声对离散扰动观测器的影响。文献[13]为了解决加速度计算中的噪声问题,提出了基于速度信息扰动观测器设计。虽然提高了对噪声的敏感度,但是由于缺少外环控制使得系统容易不稳定。

Kalman滤波器是解决传感器量化误差和测量噪声问题的有效方式[16-18]。Kalman滤波算法复杂,计算量较大,在实际系统中难以实现,更高速MCU的出现使这一问题得到一定的解决。同时该算法实现的转速估计能够适应更宽的测速范围,甚至能够在较低的速度下完成。

因此,考虑到在系统存在转速测量噪声情况下,提高伺服系统的抗扰性,本文提出一种新型的将电机转速估计和负载扰动转矩在线观测相结合的实施方案:采用Kalman滤波器观测电机转速代替位置微分计算值作为扰动观测器的输入,扰动观测器估计的负载转矩值反馈到输入端,对转矩电流进行前馈补偿。与传统的扰动观测器方案进行了对比,分析其扰动抑制性能及对噪声的敏感度。仿真和实验结果表明了所提方法的有效性。

1 扰动观测器设计

扰动观测器将外部干扰力矩的观测值引入到控制输入端,形成相应补偿,实现了对扰动的完全抑制。永磁伺服系统扰动观测器的观测方程主要是基于永磁同步电机的机械运动方程:

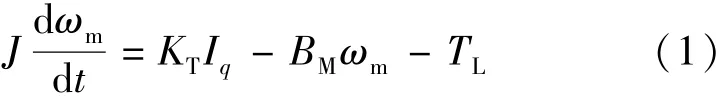
式中:ωm为转子机械角速度;KT为转矩常数;Iq为交轴电流分量;TL为等效负载转矩;J为电机转动惯量;BM为粘滞摩擦系数。系统建模时,可以忽略较小的粘滞摩擦系数的影响,构建一阶扰动转矩观测器的数学模型:

式中:Jn为扰动观测器设计时采用的电机转动惯量;KTn为扰动观测器设计时的转矩常数;g为一阶低通滤波器的截止频率。此一阶低通滤波器的引入在一定程度上可以削弱由转速微分带来的量化误差,同时可有效减小电流噪声和编码器误差对扰动观测器的负面影响,但是此扰动观测器内部仍存在纯微分运算环节,因此可将式(2)进一步变化,得到改进后的扰动观测器数学模型:

根据式(3)可重构具有负载转矩扰动观测器的速度控制系统结构,如图1所示。该系统在观测扰动转矩时不再需要微分运算,这样就在一定程度上避免了微分带来的量化误差,从而提升了扰动观测器的扰动估计性能。

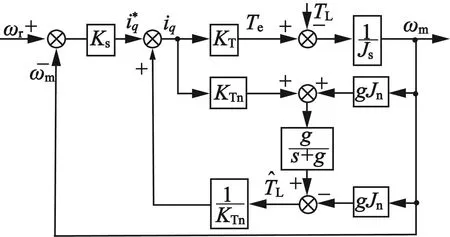
图1 具有负载转矩观测的控制系统结构图

实际设计时,需要将伺服系统离散化,其系统结构如图2所示。其中,T为扰动观测器的采样时间。由图2可得系统从参考电流到转速输出ωm的脉冲传递函数:

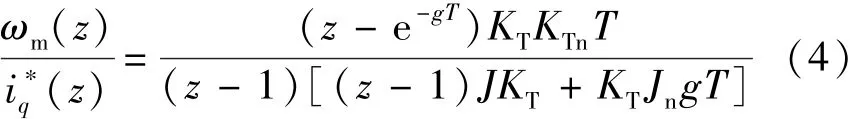
图2 转矩观测器的离散化实现形式

由式(4)可知,系统极点分别为z1=1,z2=λgT,其中λ=KTJn/JKTn。实际中,不仅要求系统保持稳定,而且也要避免出现振荡。由控制理论可得,在离散域中要求系统的极点配置在实轴(0,1)之间。即:

由于扰动观测器设计时的转矩常数KTn和实际的电机转矩常数KT基本相同,因此λ可以定义为设计观测器所用惯量和电机实际惯量之比,即λ=JMn/Jm。式(5)给出了λ,一阶低通滤波器截止频率g和采样时间T的关系,为实际的扰动观测器参数选取提供了数学依据。

2 Kalman转速观测器设计

本节采用Kalman滤波的转速估计方法,相对于传统测速算法,虽然结构较为复杂,但该算法实现的转速估计能够适应更宽的测速范围,甚至能够在较低的速度下完成。

由永磁同步电机的机械运行方程式(1)可以构建其状态方程的基本形式:

在数字化系统中需要使用状态方程的离散化形式,如下:

式中:xk,uk和yk分别是状态变量、输入变量和输出变量的离散化形式;Ak,Bk和Ck是系统矩阵、输入矩阵和输出矩阵对应的离散化形式;Wk是引入的系统噪声;Vk是引入的测量噪声。一般情况下,认为Wk和Vk是均值为0且互不相关的高斯白噪声,但实际中由于扰动等因素的影响,假设并不成立,均为有色噪声。

Kalman滤波递推迭代过程可以划分为预测过程和校正过程。

(1)预测过程:即时间更新过程,已知系统在第(k-1)个时刻的状态值,预测系统在第k个时刻的状态值,即:

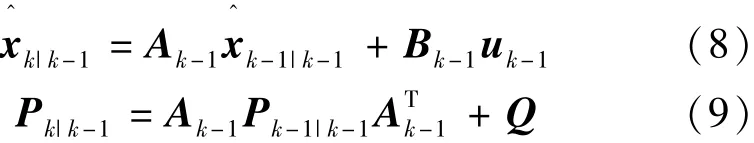
式中:P为均方误差阵,它紧跟在每个状态估计值之后以衡量估计值的可靠性。实际预测中,由于引入的系统噪声Wk是未知的,因此在计算均方误差阵P时引入系统噪声的协方差矩阵Q。

(2)校正过程:即测量更新过程,此过程是通过实际测量值对预测得到的状态先验估计值进行验证并更新,其校正公式:

噪声的协方差矩阵P可表示为:

由于校正过程中通过实际测量值对状态先验估计值进行了校正,因此,测量后状态估计值的均方差明显变小,从而增加了可靠性。在实际递推计算中,通常利用协方差矩阵Q和R取代系统噪声矢量W和测量噪声矢量V。由于响应的误差互不影响,选择Q和R为对角矩阵,即:Q=diag(Qω,Qθ,QT),R=(Rθ)。其中,Qω是角速度协方差,Qθ是角位移协方差,QT是等效负载协方差;Rθ是角位移测量误差协方差。实际应用中,矩阵Q和R中的元素的取值主要依赖实际经验,根据仿真和实验条件来选取。

将Kalman滤波器转速估计与负载转矩扰动观测器相结合,构建永磁交流伺服系统,结构框图如图3所示。系统包括电流环和速度环,控制策略采用磁场定向id=0控制。

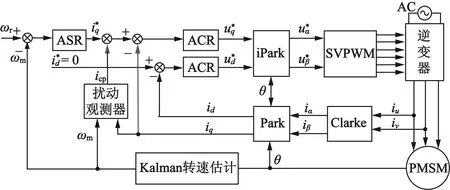
图3 转速伺服系统结构

3 仿真及实验结果分析

为验证采用负载转矩观测和Kalman转速估计相结合的伺服系统扰动抑制方案的有效性,搭建了系统MATLAB/Simulink仿真模型和实验测试平台,其中实验平台如图4所示。仿真和实验用永磁同步电机的参数如表1所示。

表1 仿真和实验用永磁同步电机参数

实验中被测电机配置分辨率为2500线的增量式光电编码器;控制器以Infineon的32bit-MCU单片机XMC 4500为核心;负载电机选用LUST公司产品,额定功率3.4 kW。转矩和转速波形通过上位机进行监测,电流波形通过示波器观测。设定伺服系统电流环控制周期10 kHz,转速环控制周期1 kHz。仿真和实验主要针对Kalman转速估计、负载转矩观测和加入控制算法后的系统速度响应3个方面进行。

3.1 基于Kalman滤波器的转速估计实验

Kalman滤波器用于观测电机转速信息,从而代替位置微分计算值,作为扰动观测器的输入。实验中同时采用常用的M法进行测速,并将两种方法所获取的转速进行对比。设定Kalman滤波器的协方差矩阵Q,P和R的初值分别为Q=diag(100,0.01,50),P=diag(0.1,0.1,0.1),R=(5)。图5和图6给出了采用2种方法当给定转速分别取20 r/min和200 r/min时对应的速度估计曲线。

图5 转速为20 r/min时速度响应曲线

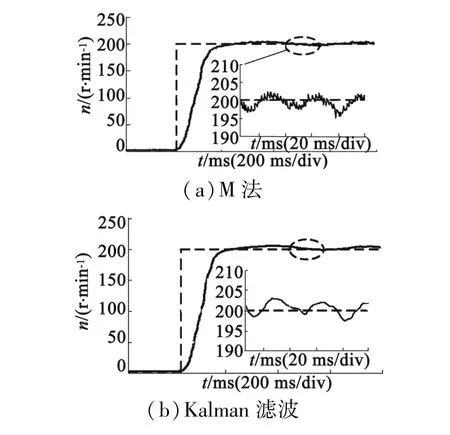
图6 转速为200 r/min时速度响应曲线

实验M法测速时加入了一阶低通滤波器,其测速精度同时受滤波器参数的影响。调节滤波器参数,使M法和Kalman滤波法所测速度波形的上升时间基本一致,进行测速精度的对比。由图5和图6可以看出,Kalman滤波算法具有较高的精度,随着转速的上升,估计误差减小,尤其在低速阶段具有更明显的优势,如本次实验给定转速20 r/min时,M法的最大估计误差约为1.4 r/min,而Kalman滤波算法的最大估计误差仅为0.7 r/min,误差率降低50%。由此可见,本文采用Kalman滤波技术可以实现全速范围的较精确的电机转速估计。

3.2 负载转矩观测实验及算法加入前后伺服系统的转速响应实验

为验证扰动观测器的转矩观测性能及所提算法加入前后伺服系统的抗扰性能,在建立的实验平台上进行了3组闭环实验:(1)传统PI调节(M法测速)伺服系统实验;(2)传统扰动观测器的扰动抑制实验(M法测速获取的转速信号输入到扰动观测器,观测负载转矩和转速响应);(3)所提算法的扰动抑制实验(Kalman滤波器估计的转速信号输入到扰动观测器,观测负载转矩和转速响应)。实验设定:系统速度给定为20 r/min,当达到稳态值后突加2 N·m负载,并在一段时间后突减负载。

(1)负载转矩观测实验

设计扰动观测器实时观测负载转矩的变化,影响其性能的主要因素为扰动观测器带宽g和输入的转速信号。首先,选定观测器带宽g。仿真时,设定电机给定转速为20 r/min,在0.05 s时突加2 N·m的扰动转矩,在0.15 s时突减负载。图7给出了当g分别取100 rad/s,500 rad/s和2 500 rad/s时负载转矩的观测波形。从图7中可以看出,g不同时扰动观测器的观测性能在快速性和准确性之间存在着折衷:带宽g越大,转矩估计时间越短,但估计误差增大。考虑此实验平台要求,选定带宽g=100 rad/s,此时估计时间相对较长,但估计误差较小。

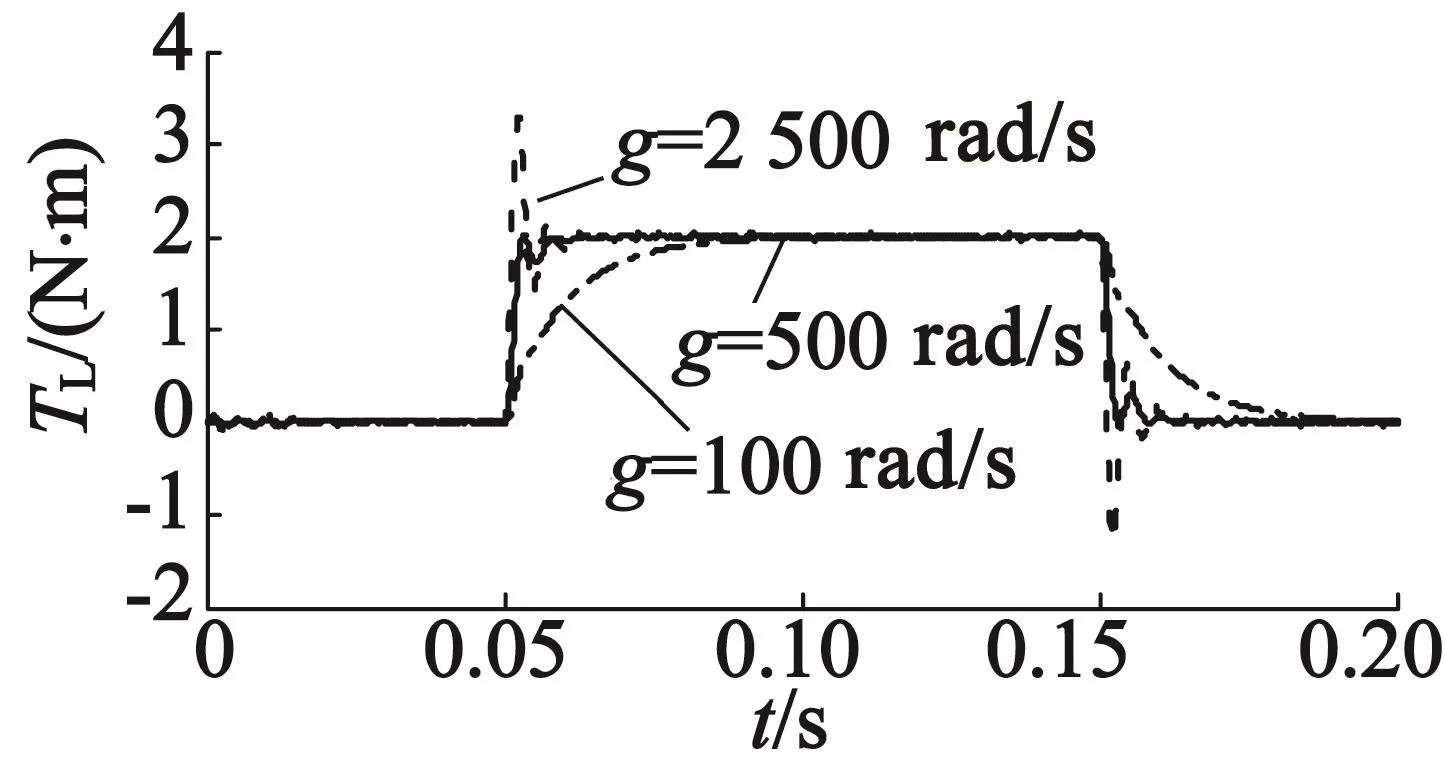
图7 不同的截止频率时估计的转矩波形

其次,观测扰动观测器输出负载转矩波形。由于Kalman滤波算法和M法获取的转速值在低速时差别较大,因此仅在给定转速为20 r/min时进行实验:采用2种方法获得转速,并作为扰动观测器的输入,待转速平稳后突加、突减2 N·m负载,此时用上位机监测负载转矩估计值的变化,如图8中所给出的第2组和第3组闭环实验(b)和(c)中估计的负载转矩波形所示。从图中可以看出,扰动观测器能实时、准确地观测出负载转矩的变化,以加载为例,采用2种方法转矩估计达到稳定的时间一致,约为1 s;转矩估计的精度却相差很大,基于Kalman滤波法由于输入转速精度较高,因而具有较高的转矩估计精度。

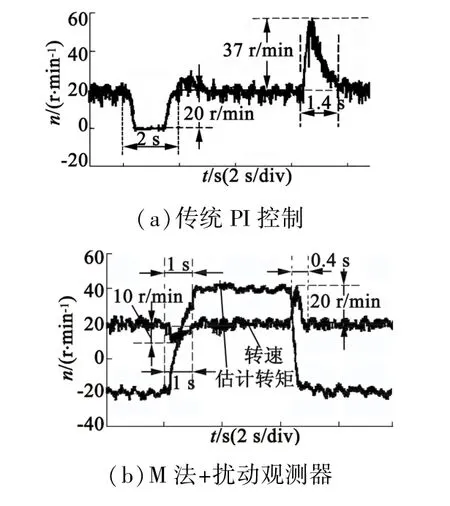
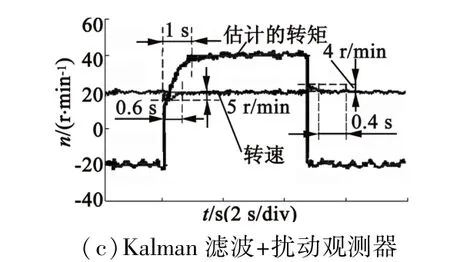
图8 扰动观测器加入前后伺服系统的转速响应

(2)算法加入前后伺服系统的转速响应实验

图8给出了3组闭环实验结果,为了清晰地对比加入扰动转矩补偿后对系统的扰动抑制作用,表2给出了图8中3组实验的对比数据。其中,补偿1表示基于M法测速的扰动补偿,补偿2表示基于Kalman滤波的扰动补偿。

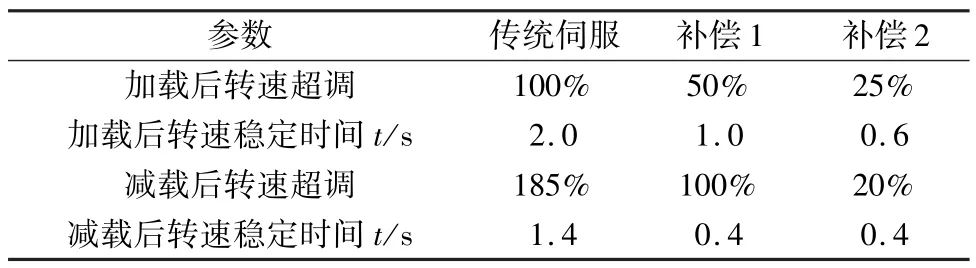
表2 实验结果对比

通过表2中的数据,做2组对比。对比1:传统伺服和补偿1。加入扰动观测器的扰动补偿后,伺服系统的鲁棒性有所改善,尤其在突减负载时:转速超调由原来的185%缩减为100%;转速超调过渡到稳定值的时由1.4 s缩短0.4 s,缩短了71.4%。但此时,传统扰动观测器由于受测量噪声的影响对系统的扰动抑制性能的改善并不理想。对比2:补偿1和补偿2。同样是加入了扰动观测器补偿,输入速度信号的质量及系统的测量噪声,对系统抗扰性能影响较大。在相同的实验条件下,基于Kalman的扰动补偿2在系统突减负载时,转速超调仅为基于M法补偿1的1/5,转速稳定时间基本一致,约为0.4 s。

4 结 语

针对影响永磁同步电机伺服系统性能的两个重要因素:负载转矩变化的不确定性和速度获取引入的测量噪声或离散误差,本文提出了基于Kalman滤波器转速估计的扰动观测器的设计,旨在提高伺服系统的控制精度和抗扰性能。实验结果表明:

(1)Kalman滤波器用于转速估计时,能有效克服噪声的影响,在全速范围特别是低速时能够准确、快速的进行估计。

(2)传统扰动观测器能够实时、准确地观测到负载扰动的变化。但由于受测量噪声等因素的影响对系统扰动抑制性能的改善并不理想。

(3)基于Kalman转速估计的扰动观测器加入系统中,能有效补偿负载扰动所引起的转速变化,减小传感器量化误差和测量噪声的不利影响,显著提高系统的抗扰性能。

参考文献

[1] HORI Y,ISEKI H,SUGIURA K.Basic consideration of vibration suppression and disturbance rejection control of multi-inertia system using SFLAC(state feedback and load acceleration control)[J].IEEE Transactions on Industry Applications,1994,30(4):889-896.

[2] KANG J K,SUL S K.Vertical-vibration control of elevator using estimated car acceleration feedback compensation[J].IEEE Transactions on Industrial Electronics,2000,47(1):91-99.

[3] 陈荣,邓智泉,严仰光.基于负载观测的伺服系统抗扰研究[J].中国电机工程学报,2004,24(8):103-108.

[4] 刘清,王太勇,董靖川,等.基于ESO及NTD的PMSM无机械传感器位置控制[J].中国机械工程,2012,23(10):1212-1215.

[5] 郑泽东,李永东,肖曦,Maurice Fadel.永磁同步电机负载转矩观测器[J].电工技术学报,2010,25(2):30-36.

[6] OHNISHI K,SHIBATA M,MURAKAMI T.Motion control for advanced mechatronics[J].IEEE/ASME Transactions on Mechatronics,1996,1(1):56-67.

[7] TAN K K,LEE T H,DOU H F,et al.Precision motion control with disturbance observer for pulsewidth-modulated-driven permanentmagnet linear motors[J].IEEE Transactions on Magnetics,2003,39(3):1813-1818.

[8] 纪科辉,沈建新.采用扰动转矩观测器的低速电机伺服系统[J].中国电机工程学报,2012,32(15):100-106.

[9] UMENO T,KANEKO T,HORI T.Robust servo system design with two degrees of freedom and its application to novel motion control of robot manipulators[J].IEEE Transactions on Industrial Electronics,1993,40(5):473-485.

[10] YAMADA K,KOMADA S,ISHIDA M,et al.Analysis and classical control design of servo system using high order disturbance observer[C]//23rd International Conference on Industrical Electronics,Control and Instrumentation,1997:4-9.

[11] GODLER I,HONDA H,OHNISHI K.Design guidelines for disturbance observer's filter in discrete time[J].Proc.of IEEE Int.Workshop on Advanced Motion Control,2002:390-395.

[12] YANG K,CHOI Y,CHUNG W K.Performance analysis of discrete-time disturbance observer for second-order systems[C]//IEEE Conference on Decision and Control,2003,5:4877-4882.

[13] TSUCHIYA A,MURAKAMI T.Characteristic Analysis of Feedback Control System with Simplified Disturbance Compensator[C]//Annual Conference of IEEE Industrial Electronics Society,2003,3:2817-2822.

[14] 刘颖,周波,方斯琛.基于新型扰动观测器的永磁同步电机滑模控制[J].中国电机工程学报,2010,30(9):80-85.

[15] 鲁文其,胡育文,梁骄雁,等.永磁同步电机伺服系统抗扰动自适应控制[J].中国电机工程学报,2011,31(3):75-81.

[16] 李剑飞,尹泉,万淑芸.基于扩展卡尔曼滤波器的异步电机转速辨识[J].电工技术学报,2002,17(5):40-44.

[17] 郑泽东,李永东,Maurice Fadel.基于EKF的PMSM无机械传感器矢量控制[J].清华大学学报,2009,49(10):1585-1588.[18] SZABAT K,ORLOWSKA-KOWALSKA T,DYRCZ K P.Extended Kalman filters in the control structure of two-mass drive system[J].TECHNICAL SCIENCES,2006,54(3):315-325.