基于社团PSO算法的异步电机参数估计方法

马 勇，刘玉春

(1.四川工程职业技术学院,德阳,618000;2.周口师范学院,周口,466001;3.西安电子科技大学,西安710071)

0 引 言

有效的异步电机矢量控制系统需要掌握电机定子和转子的电阻、漏感、互感等参数,它们对电机负载能力和转速精度的影响很大[1]。在电机的铭牌中,只有额定电压、电流、功率和转速等信息。为此需要根据这些参数来估算电机的电阻和电感参数。然而,由于电机的实际数据与铭牌数据有一定差别,致使这些估算的参数只能作为参考值[2]。为了进一步提高控制系统的准确性,所以需要对电阻和电感参数进行精确估计。

目前,电机参数估计的方法主要分为3类,即基于频率特性估计、基于时域信号估计和基于人工智能算法估计[3]。由于计算机计算能力的提升,各种智能算法得到广泛应用,例如模拟退火算法、遗传算法、蚁群优化算法和粒子群优化(以下简称PSO)算法等[4]。例如,文献[5]提出一种基于遗传算法的异步电机参数辨识方法,通过检测电机的定子电压、电流和转子转速信号简化电机模型,并利用遗传算法估计出电机的4个主要参数。

在这些智能算法中,PSO搜索最优解决方案的能力最强,且收敛速度快[6]。为此,文献[7]基于PSO算法,在线辨识出具有与直流电机相似动态特性的等效电机模型参数。然而,传统PSO算法也存在容易陷入局部最优的缺陷。为此,学者提出了一些改进型的PSO算法,例如基于局部最佳的PSO算法(以下简称PSO-l)和基于全局最佳的PSO算法(以下简称PSO-g)[8]。

本文提出一种融入社团策略的PSO(以下简称C-PSO)算法,以此提高其逃脱局部最优的能力;同时,构建了异步电机模型,推导出待估参数。以估计电流与实测电流的偏差作为适应度值,利用C-PSO算法对异步电机的定子与转子电阻、定子与转子自感、互感和等效转子转动惯量这6个参数进行估计。实验结果表明,本文方案能够准确地估计出所需参数,具有可行性和有效性。

1 异步电机的参数估计

1.1 异步电机动态模型

异步电机的参数包括定子电阻、转子电阻、定子和转子自感、互感和等效转子转动惯量。

经过三相静止-两相静止坐标变换和两相旋转-两相静止坐标变换,可得异步电机在两相静止坐标系上的数学模型[9]。其中,电压方程:

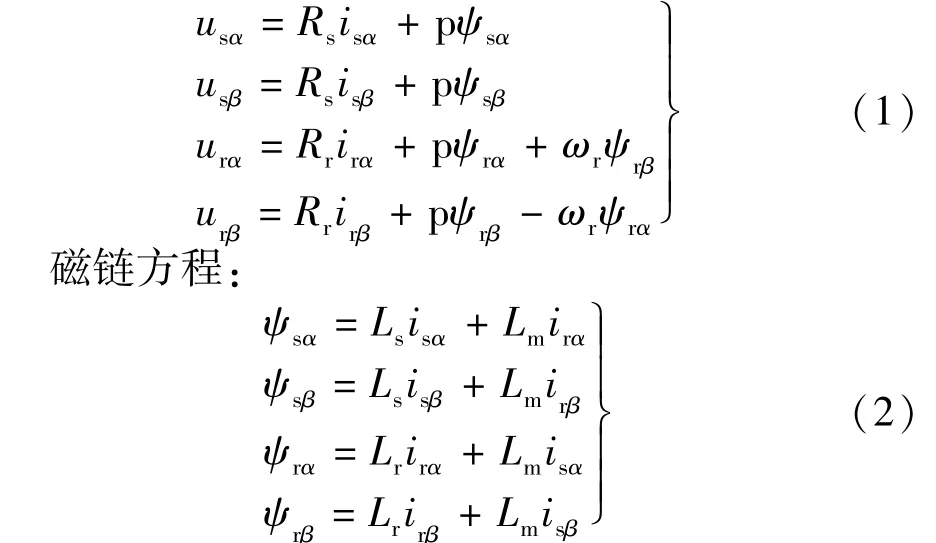
转矩方程:

转速方程:

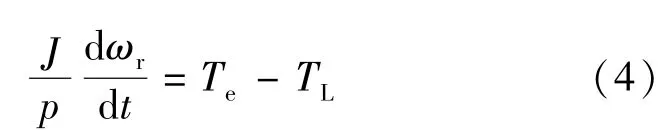
式中:isα,isβ分别为α-β静止坐标系中的定子电流;usα,usβ为定子电压;Ls,Lr分别为定子绕组自感和转子绕组自感;Lm为定子与转子绕组间的互感;Rs,Rr分别为定子电阻和转子电阻;ωr为转子旋转角速度;ψsα,ψsβ为 α-β 坐标系中的定子磁链;p 为极对数;Te,TL分别为转子转矩和负载阻转矩;J为转子转动惯量。

设定Lδ=Lr+Ls,进一步可以推导出:

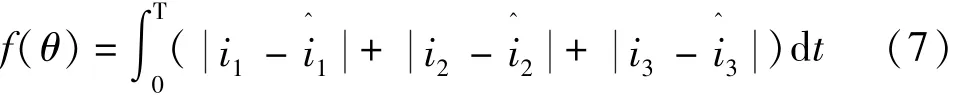
适应度值越低,说明所估计出的参数值越准确。

1.2 异步电机参数估计的框架

提出的参数估计方案框架如图1所示。通过基于直接线路或恒压频比控制(V/f)转换器的起动过程来进行测试,不同的频率会激发不同的电机动力学,而恒定的V/f几乎保持电机磁场恒定且等于额定磁场。记录起始电流的实际波形,并使用参数估计算法找出最优参数值,该最优参数值能够使根据该参数所构建的电机模型所推导的电流波形与实际波形之间的绝对误差最小。

通过上述4个待估系数,根据电机模型即可计算出所需的电机参数。

本文通过提出的C-PSO算法来求解参数估计值,并根据估计出的电机参数计算电机的电流,将估计电流与实测电流(i1,i2,i3)之间的误差值作为参数估计的适应度函数:

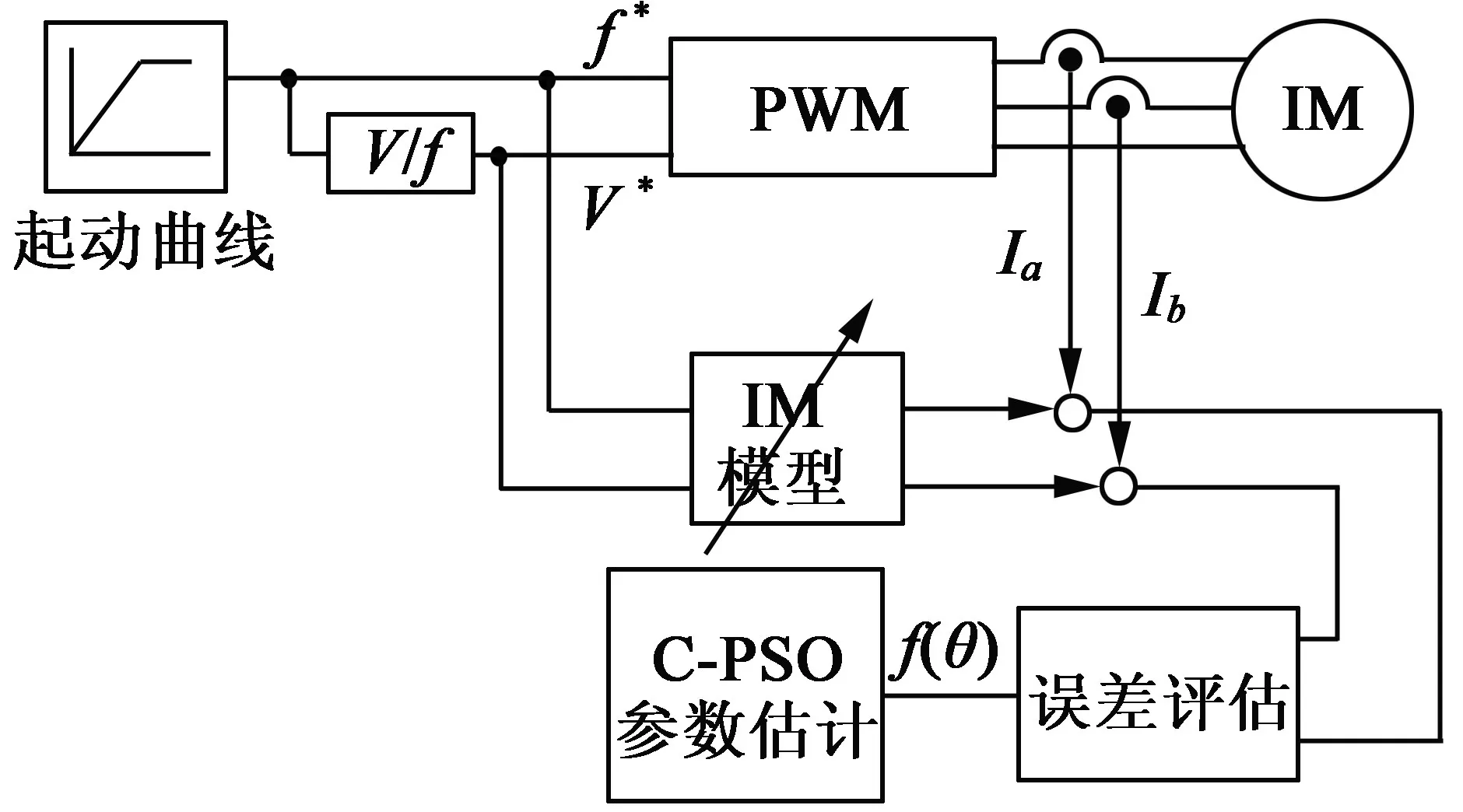
图1 异步电机参数估计的框架图

2 提出的改进型PSO算法

2.1 传统PSO算法

PSO算法是由鸟类利用其集体知识寻找食物或躲避捕食者而启发产生。粒子受其自身经验(发现的最佳位置)和邻居经验(邻居发现的最佳位置)的影响向最优位置移动。粒子i的历史最佳位置表示为pid,全局最佳位置为pgd。每一代粒子根据pid和pgd的引导,在对应区间内生成位置矢量xid和速度矢量vid,表达式如下[10]:

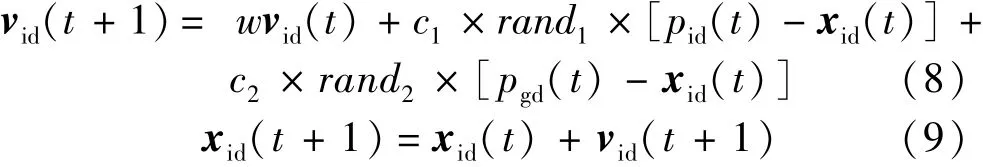
在式(1)中,c1和c2分别为个体和全局学习因子;rand1和rand2为[0,1]内的随机数;w表示惯性权重,决定对当前粒子速度继承的程度。

2.2 提出的C-PSO算法

传统PSO算法中的粒子在同一个群体中进行进化,如果在进化初期就出现一个适应度很高的粒子,会强烈影响其它粒子向其运动。这不利于粒子探索其它未知空闲,而形成过早收敛。为此,本文提出一种基于社团的PSO算法(C-PSO),将粒子群分成若干了社团,每个粒子都可以参加一个以上的社团,且每个社团都可以容纳任意数量的粒子。在寻找全局最优时,如果一个粒子相比于其邻域内的其它粒子具有较优的性能,则迫使其随机离开一个社团,以此来减少这个粒子对其它粒子速度的强大影响,从而避免过早收敛。另一方面,如果一个粒子的性能较差,即它是其邻域内性能最差的粒子,则使其随机再加入一个社团,以扩大它的社会网络,以此增加其从更好粒子中学习的机会。

提出的C-PSO中,在初始化粒子的位置和速度之后,每个粒子随机加入预定义数量的社团。接着,评估粒子的当前值并相应更新粒子的最佳局部位置。在更新粒子速度时,每个粒子受其最佳位置和其领域内所有邻居发现的最佳位置的影响。这里,粒子的邻域为包含该粒子的所有社团的集合。在速度和位置更新之后,评估粒子的新位置并重复此循环。

本文每一次迭代中都重复执行加入和离开社团步骤,所以如果一个粒子在其领域内持续表现为较差的性能,则它将一个接一个地加入更多的社团,直到达到它所允许的最大社团数量。而如果一个粒子在每个社团中持续表现为较优的粒子,则使其一个接一个地离开社团,直到达到它所允许的最小社团数量。

在加入或离开社团后,其领域内不再有极端性能的粒子,提高了算法的稳定性和平滑性。另外,本文每rr次迭代做一次检查,以找到没有表现出极端性能,但所在社团数量高于或低于默认数量的粒子,然后将其带回默认数量。

本文提出的C-PSO算法伪代码如下描述。

算法1 C-PSO算法伪代码

启动

初始化粒子和社团

While(终止条件)do

评估粒子适应度f(x),并更新pid;

for i=1到粒子数do

pgd=最佳neighbor si;

for d=1到维数do

vid=w×rand1×vid+c1×rand2×(pid-xid)+c2×rand3×(pgdxid);

xid=xid+vid;

end if

end for

更新邻域

for j=1到粒子数do

if(xj为最佳 neighbor si)且(|membershipi|＞min_membership)

then随机离开一个社团

if(xj为最差 neighbor si)且(|membershipi|＜max_membership)

then随机加入一个社团

if(|membershipi|≠default_membership)且(remainder(iteration/rr)=0)

then更新membershipj

end for

itermation=itermation+1

end while

算法1中,neighbor si为粒子 i领域的集合,membershipi表示粒子i所在社团的集合,|membershipi|表示粒子i所在社团的数量。min_membership和max_membership分别为粒子的最小和最大允许加入的社团数量。default_membership为粒子允许加入的默认社团数量。

3 实验及分析

3.1 参数设置

在一个异步电机上进行实验,电机的实际参数如表1所示。在利用C-PSO算法对参数进行估计前,需要初始化参数为一个随机值,该过程中各参数的取值范围如表1所示。

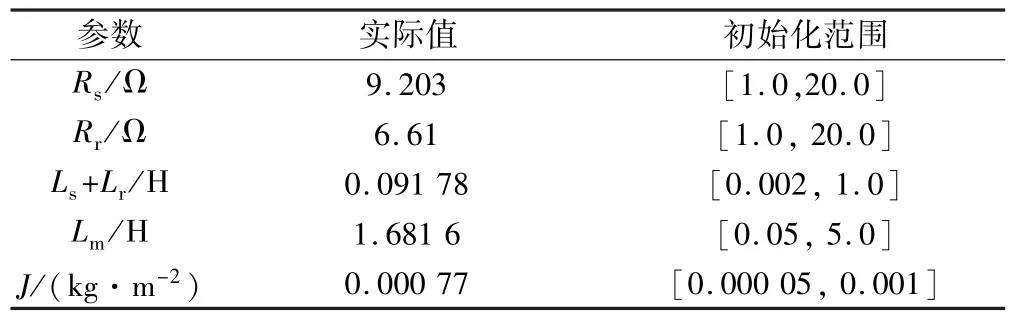
表1 电机参数的实际值和在估计中的初始化范围

为比较起见,本文将C-PSO与3种不同的算法进行比较:(1)传统一维线性搜索算法(LS);(2)基于局部最佳拓扑的改进型PSO算法(PSO-l);(3)基于全局最佳拓扑的改进型PSO算法(PSO-g)。本文在解空间的初始化范围内随机初始化这3种改进型PSO的粒子种群和粒子初始速度。C-PSO的参数如表2所示。PSO-l和PSO-g的基本参数与C-PSO一致,但其中惯性权重值w=0.729,为C-PSO算法的一半。这是因为C-PSO算法的粒子速度更新公式中,w会乘以一个均匀分布的随机数rand1,该随机数的平均值为0.5,即w预期值与其它2种算法是相同的。

表2 各种改进型PSO算法的参数值

对于LS算法,其为一种简单的确定性局部搜索技术。在该方法中,利用第i维的单元尺寸表征其搜索空间。在离散搜索空间中选择随机点(x),并评估其适应度,同时评估其领域点的适应度,如果最佳邻域的适应度小于或等于x,则该算法移动这个新点并评估其邻域的适应度。但如果最佳领域的适应度高于x,则算法终止。对于n维空间中的点x=(x1,x2,…,xn),Nx邻域集合包含2n个点。在第i维的2个方向中,通过移动一步δi来确定集合中的每个点。 Nx=(x1±δ1,x2,…,xn),(x1,x2±δ2,…,xn),…,(x1,x2,…,xn±δn)。

该算法包含一个参数,即步长δi。对于当前应用,本文将这个值设置为表1中相应维数初始化范围的0.1%。

3.2 结果分析

图2为PSO-l,PSO-g,LS和C-PSO这4种算法的适应度值随算法迭代时间的变化曲线。可以看出,经过1 000次迭代,提出的C-PSO算法最终能够达到最优的适应度值,约为0.001 9,即所获得的参数估计值的准确性最高。PSO-l算法第2,PSO-g算法第3,LS算法性能最差。

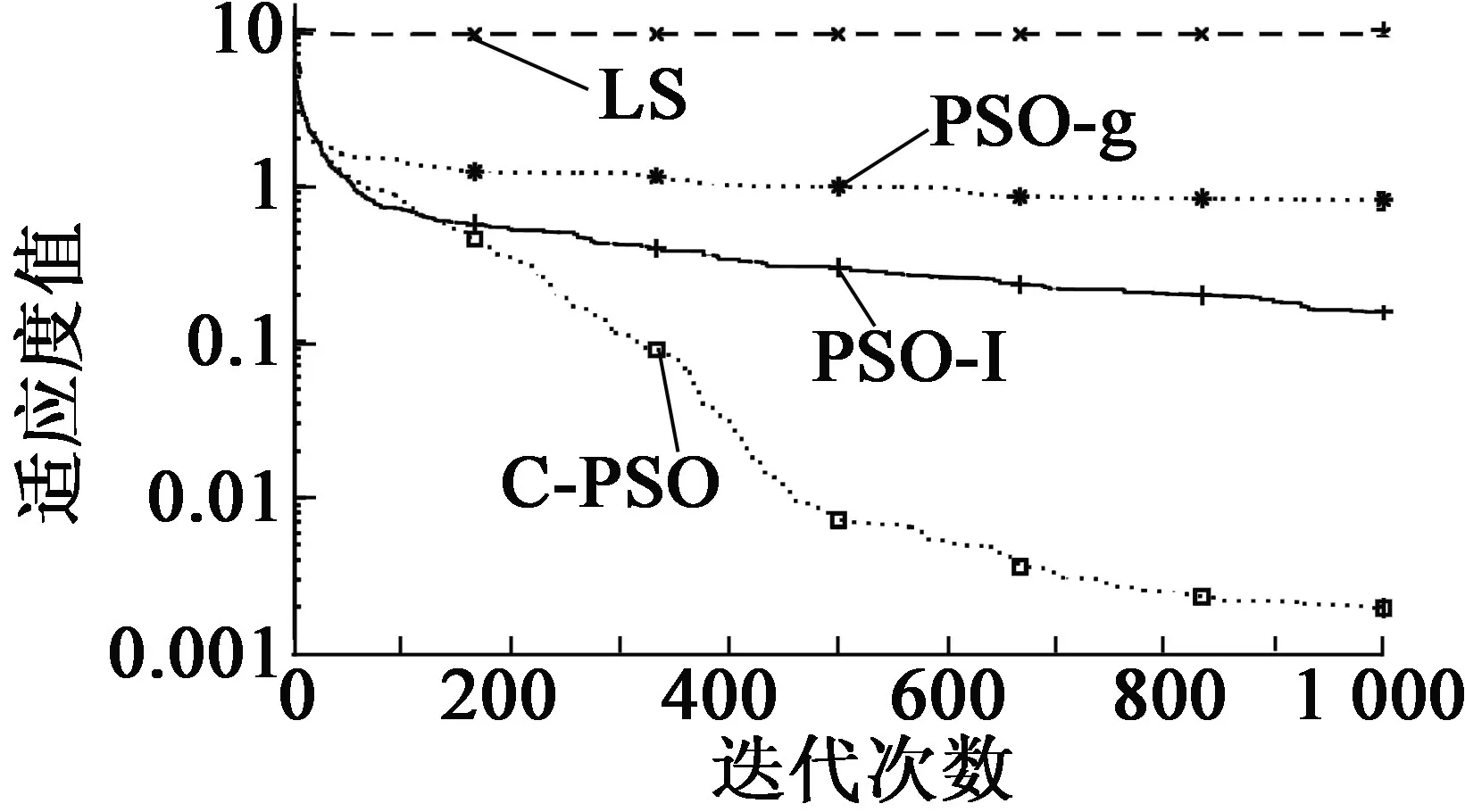
图2 各种算法的适应度值收敛曲线

这是因为,LS算法完全缺乏逃脱陷入局部极小值的能力。在所有仿真运行中,该算法被困于第1个局部最小值中。PSO-g和PSO-l算法逃脱局部极小值的能力优于LS算法,在200次迭代后,这些算法的适应度小幅下降以趋于稳定。但PSO-g算法根据粒子个体最优和全局最优来进化粒子,随着粒子进化,粒子间多样性丢失,表现出强烈的趋同性,易陷入局部最优。而PSO-l算法的学习对象不是整个群体,只是学习与其具有一定关系的相关粒子,所以其寻优能力比PSO-g的较好。本文C-PSO算法中融入了社团策略,使其逃脱局部最小值的能力优于其它所有算法,所以能够收敛到很低的值。

另外,本文C-PSO算法的收敛速度却不是最快的,约在500次迭代后能够收敛到较优的值。由于电机的参数估计只需要执行一次,没有实时性要求,对估计算法的计算时间要求不高。所以,与估计准确性相比,稍高的估计时间无关紧要。

进行20次相同实验,记录各种算法的最终适应度值,并计算出平均适应度值和标准差,结果如表3所示。可以看出,C-PSO算法的适应度值最低且标准差也最低,证明了C-PSO算法能够求解出最优解,且每次获得的最优解都较为接近,求解稳定性好。

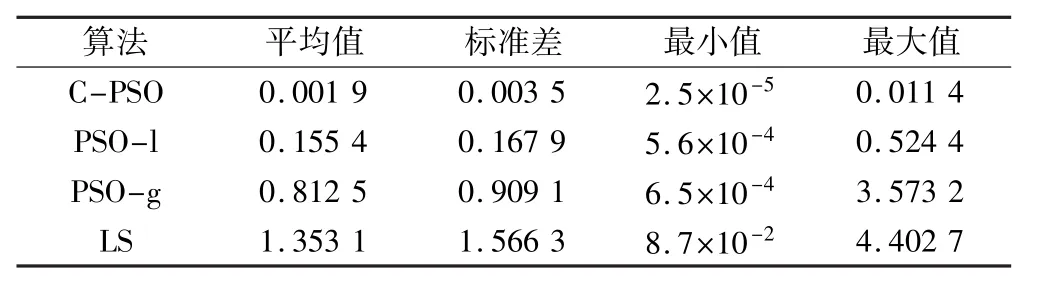
表3 各种算法的适应度值

为了比较算法对各参数估计的准确性,同样记录这20次实验中各种算法估计出的6个参数值,并计算其与实际参数值的平均百分偏差,结果如表4所示。可以看出,本文C-PSO算法估计出的电机参数值与实际值之间的差异最小,进一步说明了CPSO算法具有优越的求解准确性。

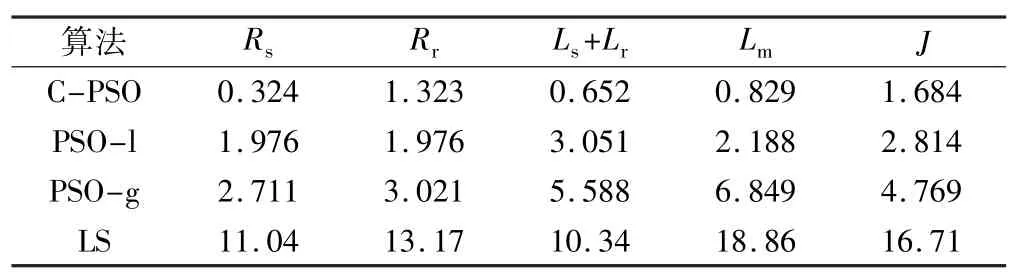
表4 各种算法所估计参数值与实际值的平均百分偏差(%)

4 结 语

本文对于异步电机参数精确估计的问题,提出一种改进型的PSO算法。融入社团策略来提高传统PSO算法逃脱局部最优的能力,以此获得最为准确的估计参数。通过参数估计,并将估计参数与实际参数进行比较,结果证明了本文方案的有效性。

参考文献

[1] 张俊华.异步电机的参数辨识与矢量控制[J].杭州电子科技大学学报,2011,31(4):132-135.

[2] 李勇,李智,牛军浩,等.基于矢量控制的异步电机参数离线辨识策略[J].微特电机,2016,44(1):64-67.

[3] BILSKI P.Application of support vector machines to the induction motor parameters identification[J].Measurement,2014,51(1):377-386.

[4] 杨建辉,吴聪.PSO结合SA优化算法的无线传感器网络路由协议[J].湘潭大学自然科学学报,2015,37(4):98-104.

[5] 肖曦,王雅婷,许青松,等.一种基于遗传算法的异步电机参数辨识方法[J].电工技术学报,2013,28(1):331-335.

[6] MOHAMMADI H R,AKHAVAN A.Parameter estimation of threephase induction motor using hybrid of genetic algorithm and particle swarm optimization[J].Journal of Engineering,2014,23(4):142-148.

[7] EMARA H M,ELSHAMY W,BAHGAT A.Parameter identification of induction motor using modified Particle Swarm Optimization algorithm[C]//IEEE International Symposium on Industrial Electronics.2013:841-847.

[8] 史朝亚.基于PSO算法无线传感器网络覆盖优化的研究[D].南京:南京理工大学,2013:23-27.

[9] 戴亮,黄志远,陈业明,等.静止状态下异步电动机参数离线辨识方法[J].微特电机,2014,42(2):33-36.

[10] TOFIGHI E M,MAHDIZADEH A,FEYZI M R.Online estimation of induction motor parameters using a modified particle swarm optimization technique[C]//IECON 2013-39th Annual Conference on Industrical Electronics Society.IEEE,2013,20(11):3645-3650.