具有投资收益的多险种复合负二项风险模型的破产概率

魏 静，葛世刚，仓定帮

(华北科技学院 基础部，北京 东燕郊 101601)

具有投资收益的多险种复合负二项风险模型的破产概率

魏 静，葛世刚，仓定帮

(华北科技学院 基础部，北京 东燕郊 101601)

在经典风险模型的基础上，考虑到投保集体的不同质性，建立了保费收取过程和理赔过程均为负二项过程、投资收益率为常数的多险种随机风险模型，通过分析盈利过程的性质，得到终极破产概率的计算公式和破产概率上界的Lundberg不等式,特别地，给出了两险种时，保费和理赔额服从指数分布下破产概率的精确表达式。结果表明：在投资收益一定时，保险公司增加用于投资的金额，可以降低破产概率，从而规避风险。

多险种；投资；负二项过程；指数分布；破产概率

0 引言

破产概率的研究一直是保险风险研究的一大热点，经典风险模型往往只考虑单一险种的破产问题，随着保险市场的多元化，保险种类的多样化，越来越多的学者开始对经典的风险模型从不同的角度进行推广，简而言之，近年的文献主要从以下几个方面对风险模型进行了推广：(1)考虑两种及以上的保险种类；(2)加入干扰项；(3)考虑利率的影响；(4)考虑退保的影响；(5)考虑投资收益。文献[1-3]研究了两险种风险模型的破产概率；文献[4]对保费收取服从不同的随机过程的角度建立了多险种风险模型，得到了破产概率的计算公式；文献[5]考虑了干扰条件下复合Poisson Geometric过程的多险种风险模型下的破产概率；文献[6]将退保因素考虑进来，建立了退保影响下的多险种风险模型，通过分析盈余过程的性质，得到了破产概率的表达式和破产上界；随着保险经营的多元化，保险公司会考虑将一部分资金拿去做投资，投资就会有风险，考虑带有投资收益的多险种风险模型则更为合乎实际，文献[7-8]研究了带投资收益的多险种风险模型的破产概率。本文在以上的基础上，考虑到在实际的风险中，保单的不同质性，保费收取的次数和理赔次数的期望和方差不一定相等，建立了保费收取和赔付服从负二项过程、带投资收益的多险种风险模型，通过分析盈余过程的性质，得到破产概率公式和破产上界的Lundberg不等式。

1 模型建立描述

在保险实务中，保费收取和理赔次数的期望和方差不一定相等，考虑到保单的不同质性，我们考虑投保次数和理赔次数均符合负二项过程，建立带投资收益的多险种风险模型：

(1)

1)u:t=0时刻的盈余，即保险公司的初始准备金；

3)Xki：第k类风险第i次的保费，i=1,2,…;k=1,2,…,n；

Mk(t):时刻t为止第k类风险收取的保费次数，服从参数为(hk,pkX)的负二项分布；k=1,2,…,n

4)Yki：第k类风险第i次的理赔额，i=1,2,…;k=1,2,…,n；

Nk(t):第k类风险时刻t为止的理赔次数，服从参数为(sk,pkY)的负二项分布；k=1,2,…,n；

5) {Mk(t):t≥0,k=1,2,…,n}，{Nk(t):t≥0,k=1,2,…,n}，

{Xki:k=1,2,…,n;i=1,2,…}，{Yki:k=1,2,…,n;i=1,2,…}相互独立；

(2)

2 盈利特性分析

引理1：盈利过程{S(t),t≥0}具有平稳独立增量。

证明：由负二项过程具有的平稳独立增量性及模型的独立性假设即可得证[3]。

3 计算与论证

引理3：对于盈利过程{S(t),t≥0}，存在函数g(r)，使得E(e-rS(t))=etg(r)，并且方程g(r)=0在(0,r)上r≥0存在唯一正解R∈(0,r)，称R为调节系数。

则E(e-rS(t))=etg(r)得证。下证方程g(r)=0在(0,r)上r≥0存在唯一正解，由

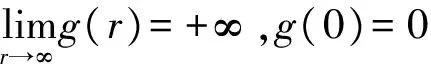
定理：本文所建立的带投资多险种随机风险模型

的最终破产概率为

证明：对于t>0和r>0，有

E[e-rU(t)]=e-ruE[e-rS(t)]，取r=R，则

E[e-RU(t)]=e-Ruetg(R)=e-Ru，故由条件期望公式有，

(3)

对于给定的T≤t，

U(t) =U(T)+U(t)-U(T)

下证(3)式右端第二项为0，令

(4)

由切比雪夫不等式，得

当t→∞时，(4)式→0，故

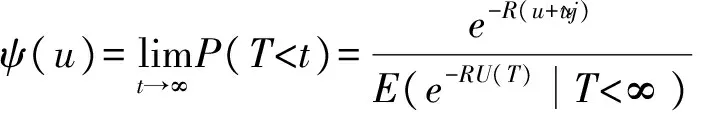
特殊地，当取n=2时，可以得到：

推论2：带投资双险种复合负二项风险模型中，若个体理赔额Y1i,Y2i(i=1,2,…)独立同分布且分别服从参数为α1>0,α2>0的指数分布，收取的保费X1i,X2i(i=1,2,…)独立同分布且分别服从参数为β1>0,β2>0的指数分布，则最终破产概率为

其中R是方程

的唯一正解。

证明：设Z=Y1i+Y2i，其概率密度函数为fz(z)，由卷积公式可得

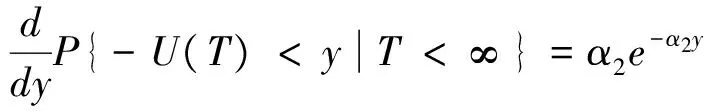
从而有

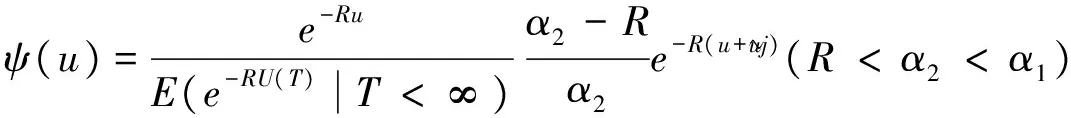
4 结论

本文考虑到保险经营的多样性，利用负二项分布期望和方差不相等的性质，建立了带投资的多险种复合负二项风险模型，对经典风险模型进行了推广：

1) 考虑了n个相互独立的险种，更具一般性；

2) 考虑到实际保险业务中，保费收取次数与理赔次数的期望和方差不一定相等，引入更加符合实际的负二项过程；

3) 为了提高经营的稳健性，考虑了将资金进行再投资，在投资收益率一定的情况下，增加投资金额，可以降低破产概率，这与实际相吻合。

[1] 陈凤丽, 施齐焉. 一类双险种风险模型的破产概率研究[J]. 福州大学学报(自然科学版), 2012, 40(4):449-452.[2] 赵金娥, 王贵红, 龙 瑶. 一类双险种风险模型的破产概率[J]. 西南师范大学学报(自然科学版), 2013, 38(1):16-21.[3] 魏静, 桂文永, 刘海生. 双险种复合负二项风险模型破产概率的研究[J]. 华北科技学院学报, 2012,9(2):81-84.

[4] 曲中宪, 徐中海, 武文华. 随机投保费下多险种破产模型的研究[J]. 东北师范大学学报(自然科学版), 2010, 42(1):18-21.

[5] 于文广, 黄玉娟. 干扰条件下复合Poisson-Geometric过程的多险种风险模型下的破产概率[J].山东大学学报(理学版),2008,43(2):16-18.

[6] 王永茂, 高 阳, 李 杰. 退保因素影响下多险种风险模型的破产概率[J]. 扬州大学学报(自然科学版), 2012, 15(3):20-26.

[7] 乔克林, 侯致武. 考虑投资的双复合二项风险模型的破产概率[J]. 延安大学学报(自然科学版),2011,30(3):32-34.[8] 管伟青, 牛铭. 常利率下带投资和干扰风险模型[J]. 佳木斯大学学报(自然科学版), 2013,31(1): 137-139.

Ruin probability of multi-type compound negative binomial riskmodel with investment profit

WEI Jing, GE Shi-gang, CANG Ding-bang

(DepartmentofBasicCourses,NorthChinaInstituteofScienceandTechnology,Yanjiao,101601,China)

Based on classic risk model，considering the non homogeneity of the policyholders, a multiple stochastic risk model was established with negative binomial process for the premium collecting frequency and claim frequency and the rate of return on investment be constant. Through analyzing the properties of the profit process, it obtains the ultimate ruin probability and the Lundberg inequality formula of upper bound for ruin probability. In particularly, the exact expression of probability was obtained for two-type insurance with premiums and claims in exponential distribution. The results show that when the investment income is certain, the insurance company can reduce the ruin probability by increasing investment to avoid risks.

multi-type insurance; investment; negative binomial process; exponential distribution; ruin probability

2016-12-26

廊坊市科技局科学技术研究与发展计划自筹经费项目(2016011031, 2016011048,2016013113)

魏静(1980-)，女，河北邢台人，硕士，华北科技学院基础部讲师，研究方向：风险分析。E-mail：weijing_jcb@ncist.edu.cn

O211.6

A

1672-7169(2017)01-0106-04