封闭人群生存人数整体预测

王志刚　王晓军　张学斌

摘要：由不同组别人群组成封闭人群整体生存人数的预测是相关经济、社会问题研究的基础。现有文献在研究相关问题时，使用的方法为：首先根据动态死亡率模型对其中具有相同特征不同部分的生存人数进行预测，之后通过加总得到整体人数的预测（简称现有方法）。由于现有方法忽略了不同特征人群死亡率变动间相关性的影响，会低估生存人数的波动性。本文使用Lee-Carter模型，在将封闭人群按性别分组的基础上，给出了构建生存人数整体预测模型的过程和实例。并通过理论分析和数值模拟两个视角对现有方法和新方法做了比较。比较结果指出：在死亡率波动具有广泛相关性的现实世界中，只有在均值预测时，现有方法才可以达到预期效果，因此笔者建议在对整体人数（特别是涉及方差和分布函数）预测时，使用本文介绍的整体生存人数预测模型。

关键词：生存人数：Lee-Caner模型：整体预测

中图分类号：C921

文献标识码：A文章编号：1000-4149（2016）04-0010-11

DoI：10.3969/j.issn.1000-4149.2016.04.002

一、引言

对于不考虑人口流动的封闭人群生存人数预测是相关经济、社会问题研究的基础。封闭群体人数的变动主要来自于死亡所引发的成员退出。封闭人群通常是由不同特征（例如不同性别、不同地域）人群构成。在对封闭人群生存人数进行预测时，现有文献中主要根据某一特征对人群进行分组，在对每一组生存人数预测的基础上，通过加总得到整体人数的预测。简单加总的前提条件是不同特征人群死亡率变动间不具有相关性。而实际经验和数据都显示，不同特征人群死亡率变动是具有相关性的。简单地忽略人群死亡率变动间相关性的影响，虽然在对生存人数期望研究时可以得到比较满意的效果，但对方差、特定分位数和分布函数的预测就变得不再适合了。而随着社会问题研究的深入，一些领域（例如保险精算）的研究不仅需要获得生存人数的期望值，还需要获得生存人数波动方差和分布函数。在现有研究方法无法满足对方差、分位数和分布函数度量的情况下，本文将以动态死亡率模型为基础，将不同组别问相关性纳入到模型中，建立新的生存人数预测模型，以满足实际问题研究的需要。

建立一个整体生存人数预测模型，需要完成两方面的工作：一是将影响人口变动的死亡率模型由一维扩展为多维；在由一维扩展到多维时，就必须考虑不同组别间死亡率变动时体现出的相关性，因此第二项工作就是在分组的基础上，准确度量不同组间死亡率变动的相关性，并将相关性研究结果纳入到前面建立的多维死亡率模型中。

由于一组人群可以按不同指标分为不同组，作为整体生存人数预测实例，本文按照性别将相同年龄人群分为两组。在展开具体问题研究时，与前面提及的逻辑顺序不同，本文首先对不同性别死亡率变动过程中表现出的相关性进行深入研究：然后，将得到的相关性度量结果纳入多维Lee-Carter动态死亡率模型中，进而得到按性别分组的整体生存人数预测模型；最后对现有研究方法和本文方法的预测结果进行对比研究。

二、男性和女性死亡率的相关性

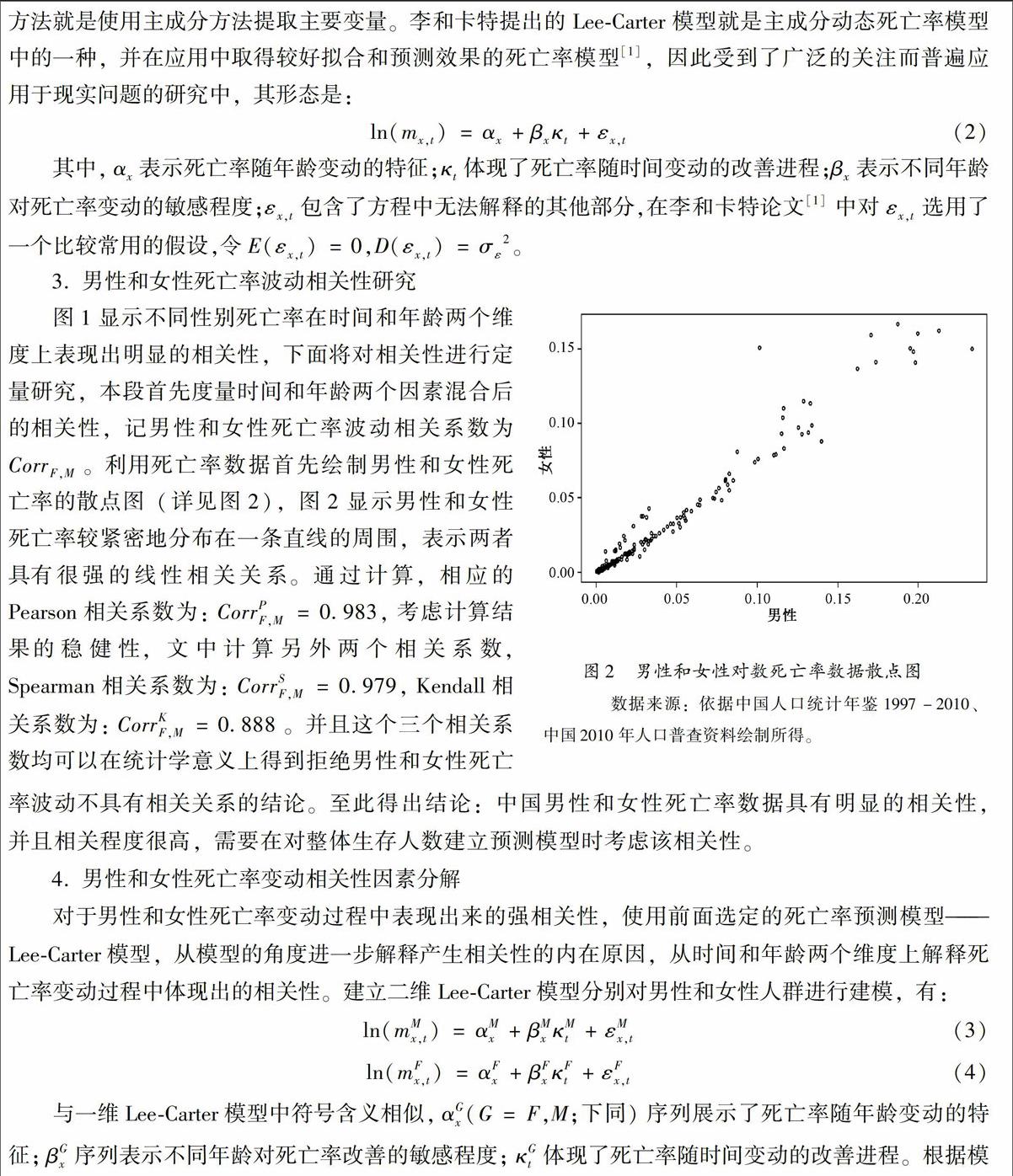
剔除了人口再生产引发的成员增加和人口迁移引发的成员数的变动，此时封闭人群生存人数变动主要来自成员由于死亡而引发的退出。本节将对引发成员退出的（男性和女性）死亡率变动过程中体现出的相关性进行研究。为了后面陈述方便，先对需要使用的符号、数据和死亡率模型进行简要的

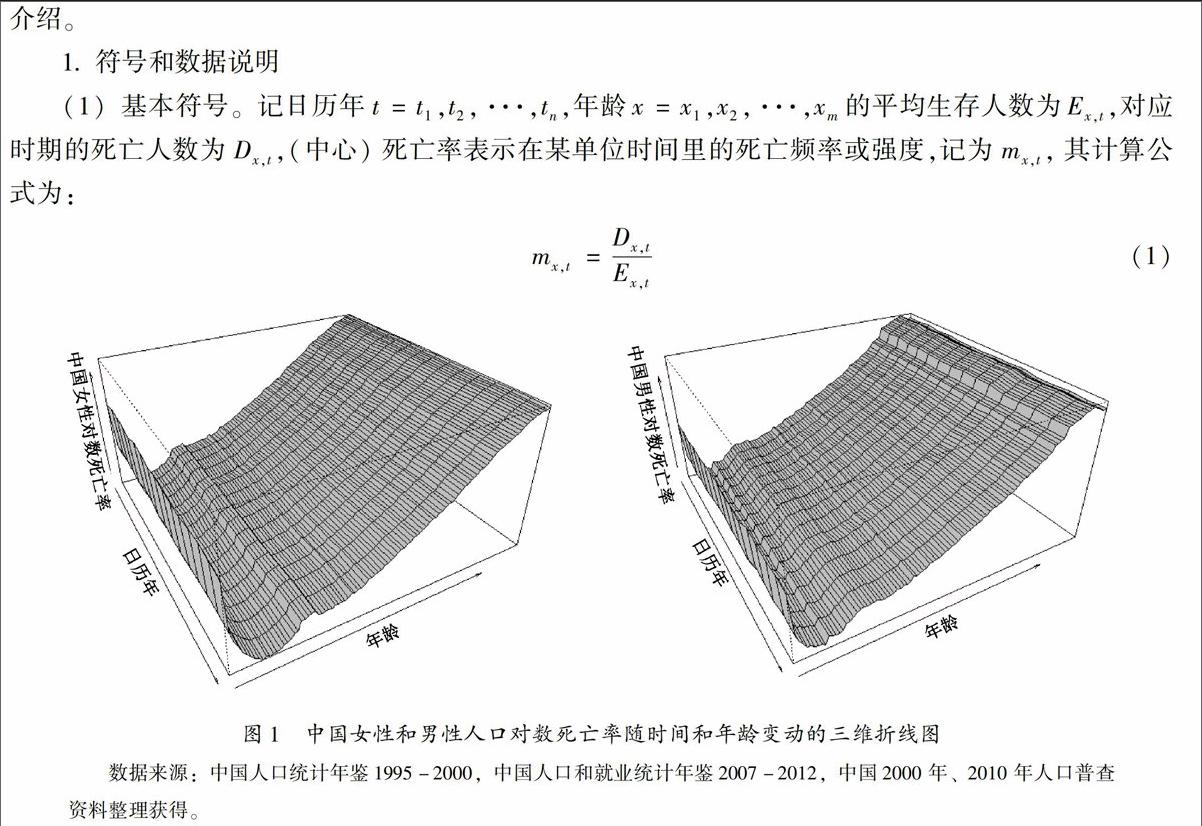
（2）数据。本文建模使用的数据来源于国家统计局公布的1995-2006年《中国人口统计年鉴》、2007-2012年《中国人口和就业统计年鉴》和2010年人口普查数据中的全国分年龄、分性别死亡人口状况表，进而根据式（1）计算得到1995-2012年各年度分年龄（0-85岁五岁一组）、分性别的中心死亡率。为了更清晰地描述这些数据，图1给出了我国1995-2012年連续16年0-85岁的男性和女性对数死亡率的三维图。图1显示中国男性和女性对数死亡率变动具有很强的相似性，这种相似性体现了内在相近的生理特征和共同的社会、医疗水平对男性和女性死亡率改善的内在规律，这提示我们在建立整体生存人数估计时应该考虑相关性的影响。

2.动态死亡率预测模型

在将男性和女性死亡率波动过程中的相关性纳入死亡率模型之前，首先需要选取一个合适的死亡率模型。常用的死亡率模型可以分为静态和动态死亡率模型两种，由于静态死亡率模型不包含时间项所以无法用于预测，因此为了能够对未来的生存人数进行预测，需要使用动态死亡率模型。

近30年来，动态死亡率模型在理论上取得了丰富的研究成果，其中包括：李（Lee）和卡特（Carter）1992年提出的Lee-Carter模型，伦肖（Renshaw）和哈伯曼（Haberman）2006年提出的Lee-Caner改进模型——RH模型，以及凯恩斯（Cairns）等人2006年提出的CBD模型。王晓军、黄顺林汇总介绍了包括以上模型在内的8个动态死亡率模型。王志刚指出一个较为理想的形态应该包含年龄项、时间和年龄交互影响项，以及出生年因素项。为了减少待估参数，一个较好的

动态死亡率模型中虽然没有将社会、医疗等变量直接纳入到模型中，但死亡率的变动综合体现了这些因素对死亡率的影响，因此模型中的三组参数（α_x，β_x，K_t）估计结果体现了多种因素对不同年份、年龄人群的影响合力。间接体现了社会、医疗等因素变动的影响，并且在实际问题中取得了较好的拟合效果，其参数含义清晰。因此，动态死亡率模型受到了广泛关注，其中Lee-Carter模型就被联合国人口署和美国人口普查局等众多机构使用，后面就以Lee-Carter模型为例，建立能够反映男性和女性死亡率变动相关性的封闭人群生存人数整体预测模型。

三、建立生存人数预测模型

1.建立男性和女性整体死亡率预测模型

李和卡特提出的一维Lee-Carter模型最早用于美国男性人口死亡率建模，之后学者在引用该方法时，也都只限于对某一组别人群进行研究。国内研究也体现出相同特点。本文需要使用二维Lee-Carter模型对男性和女性生存人数进行整体建模，这就需要对前面选取的一维Lee-Carter模型进行扩展，建立一个能够体现死亡率变动内在相关性的死亡率联合模型，以使模型能够更好体现中国男性人口和女性人口死亡率随年龄波动的自然规律及人口死亡率改善进程中的同步性。

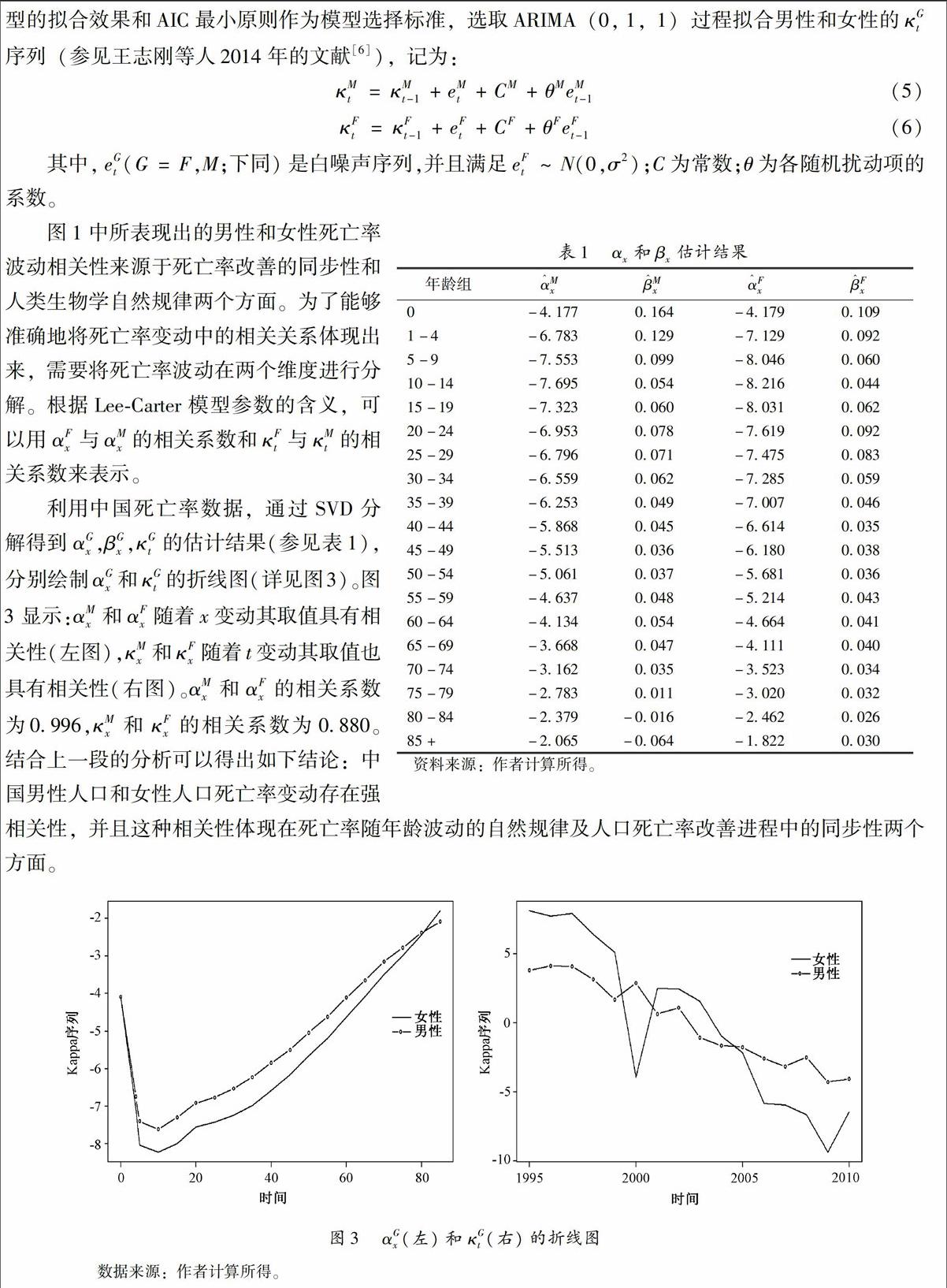
根据二维Lee-Carter模型中参数含义可知，式（3）和（4）中的α_xG项取值序列已经体现了死亡率随年龄变动的规律和相关性，此时直接在模型中使用估计值便可以满足要求，不需要在模型中再引入新的约束。

建立新旧两种方法的预测模型后，作为实例，下面以社会养老保障和（养老）保险公司关注的老年群体为例，假设2012年初始年龄为60岁的男性和女性各10000人为例，使用前面给出的整体生存人数预测方法，对未来45年生存人数进行预测，并建立分布函数，计算均值、标准差和分位数。

（1）均值估计比较。图4中分别绘制了使用分性别估计和整体估计得到的未来45年内男性、女性和总体生存人数均值预测值（共计6个预测值）。但在图4中，只能清晰辨别出三条曲线，这是因为使用两种不同方法分别得到三个期望的估计值完全一致，所以其绘制出的曲线黏合在一起，无法清晰辨别。其中（由下向上第一、二）两（实际是四条线）条曲线，分别体现了两种方法估计得到的男性和女性期望的预测结果，由于相关性对不同组别生存人数的估计是不产生影响的，所以两个估计结果一致是情理之中的。另一条曲线描述了整体生存人数的期望值，由于相关性对于期望求和不产生影响，所以两个计算结果也是一样的，图形上也显示为两条曲线黏合在一起（由下向上第三条线）。

（2）标准差和分布函数估计结果比较。对于期望估计结果，两种方法完全一致的效果，可能会让使用者误认为原有方法是有效的工具（但事实上这只是一个巧合，而不是正确的路径）。在需要生存人数的方差等相关数值时，现有的方法就没有这样幸运了。图5中依然分别绘制了使用分性别估计和整体估计得到未来45年内男性、女性和总体生存人数方差的估计值（共计6个估计值）。但在图5中，能够清晰辨别出四条曲线，比图4中多一条可以辨识的曲线。

图5中（由下向上第一、二）两条曲线，分别体现了两种方法估计得到的男性和女性方差的预测结果（共计4条线）。由于相关性对单个组别的估计并不产生影响，所以使用两种不同方法得到男性和女性生存人数预测值的波动方差相同，据此绘制出的四条曲线黏合在一起，只能清晰辨别出两条。另外的两条曲线就体现了使用两种不同方法对整体方差估计结果的不同，其中使用独立估计得到的男性和女性方差估计结果之和（由下向上第三条线）明显低于对整体生存人数进行预测得到的方差值（由下向上第四条线），体现了分别估计方法对方差可能产生低估的负面影响。

标准差的不同也会引发两种方法对生存人数分布函数的预测结果的不同，在独立假设下较小的标准差意味着生存人数预测结果更加集中，体型更加“轻盈”；相对应的，整体生存人数预测模型的标准差较大，得到的分布函数则会更加“丰满”（详见图6）。

依据模拟得到的结果还可以进一步估计该组人群的余寿，计算结果参见表3。估计结果显示：两种情形假设下余寿估计值是相同的，但是现有方法对于余寿波动方差的估计是明显低于考虑相关情形下的估计结果。在两种不同假设下，表3中给出的余寿90%置信区间分别为（14.28，15.36）和（14.05，15.54），现有方法得到的估计区间更窄，区间上限和下限差为1.18岁，而在考虑相关情形下得到的区间宽度为1.49岁，比现有方法高0.41岁。可见，现有的方法低估了余寿的波动范围。

五、结论

通过上述分析可以得到以下结论，现有方法和本文介绍的建模方法内含了两种不同的假设条件，本文介绍的整体生存人数预测方法更符合实际情况。虽然以Lee-Carter为代表的动态死亡率模型并没有明确包含人口生理特征和社会、医疗条件等因素项，但体现了这些因素对死亡率变动的综合影响。现有方法中在分别对男性和女性死亡率波动进行建模，并进而通过加总得到男性和女性生存人数之和的预测值时，对男性和女性死亡率分别独立建模，隐含假设这些因素是分別独立作用于男性和女性的。而现实生活中，由于内在相近的生理特征和社会、医疗等条件发生的改变同时影响男性和女性人群，使得男性和女性人群死亡率波动具有内在的关联性，因此，在进行整体生存人数建模时，假设生理特征和社会、医疗条件对男性和女性死亡率影响具有相关性，更加符合实际。本文介绍的方法能够很好地将这种相关性纳入到模型中，所以使用整体的生存人数模型进行建模将更接近实际情况。

同时理论和数值计算结果显示：本文给出的方法能够更加有效地估计整体生存人数的期望、方差和分布函数。人口估计的期望值，可以理解为在未来社会和医疗条件中性变动条件下预测生存人数。此时现有方法和本文介绍的方法将基于相同的假设条件下进行计算，所以得到的结果是一致的，但这种一致应该理解为一种巧合性的一致，不能代表现有的方法是正确的。标准差体现了死亡率改善中受到社会和医疗等因素的影响，而引发的生存人数的平均波动。分别对男性和女性死亡率波动进行建模，就意味着假设这些因素是分别作用于男性和女性。这就有可能获得假设男性人口发生死亡率改善而女性死亡率恶化的模拟结果，或是男性人口发生死亡率恶化而女性死亡率改善的模拟结果。当将男性和女性人口加总获得整体人口研究结果时，就会对冲掉生存人数的波动，使得整体波动偏差变小，从而低估风险。本文给出的研究框架，有效地纳入了死亡率变动中体现的相关性，能够更加准确地预测生存人数的变动幅度和分布函数。

本文以性别分组为例，给出了利用动态死亡率模型构建生存人数整体预测路径和实例，该框架也可以适用于其他二维分组和多维情况。死亡率变动体现的相关性不仅体现在一个地区内的不同组别的人群上。根据HMD（世界人口死亡率）数据库中的数据显示，不同地区的人群死亡率也具有很强的相关性，因此在对整体人群生存人数进行预测时，不同地域、组别人群间具有的相关性是必须应该考虑的问题，在研究这些问题时，可以参考本文的研究框架构建相应的整体生存人数预测模型。

由于经典的Lee-Carter模型被世界上多个政府、金融机构作为死亡率预测模型，本文以Lee-Carter模型为例给出的生存人数整体预测模型，有助于和国外现有相关研究成果衔接。但本文所讨论的研究思路并不局限于该模型，可以扩展到其他动态死亡率模型中，以建立相应的生存人数整体预测模型。