GNSS三频周跳探测与修复算法

刘 柳，吕志伟，于晓东，王鹏旭，杨东森，张伦东，丛佃伟

1. 信息工程大学，河南 郑州 450001； 2. 北斗导航应用技术河南省协同创新中心，河南 郑州 450001； 3. 上海司南卫星导航技术股份有限公司，上海 201801



GNSS三频周跳探测与修复算法

刘 柳1,2，吕志伟1,2，于晓东3，王鹏旭1,2，杨东森1,2，张伦东1,2，丛佃伟1，2

1. 信息工程大学，河南 郑州 450001； 2. 北斗导航应用技术河南省协同创新中心，河南 郑州 450001； 3. 上海司南卫星导航技术股份有限公司，上海 201801

针对使用组合观测值探测周跳存在不敏感周跳且难以修复的问题，研究了三频周跳探测与修复的几何原理，从几何角度研究了多个相位无几何组合(GF)探测周跳的异同，以及加入MW组合后的效果，并搜索了相应的不敏感周跳。提出了以对应的横截面积最小为原则选取组合量的方法。经北斗三频实测数据验证，GF组合的数量以两个为宜，加入MW组合后不敏感周跳进一步减少，优化选取的两个GF组合和MW组合联合探测周跳仅存在一个不敏感周跳，且探测到的周跳均能正确修复。

周跳探测；不敏感周跳；周跳修复；优化组合量；无几何相位组合

周跳探测是GNSS数据预处理的重要一环，检验了相位观测值的连续性，而周跳修复则恢复了整周模糊度的连续性。对于单频观测数据，可采用高次差法、多项式拟合等方法探测周跳，但由于未能消除接收机钟差的影响，不能探测小周跳[1-2]，且无法准确修复周跳。而GF组合消除了接收机钟差等几何误差，无需平滑便可实时探测1周的小周跳，被广泛应用于数据处理中。目前接收机一般能接收双频甚至三频信号，提供了更多的组合观测值资源[3,4-6]。

当3个载波上的跳变量与组合系数比例接近时，该周跳的探测量接近零，无法被探测[6]。这类不敏感周跳若未被探测，会一直存在于后续历元中，造成系统性偏差。文献[7]中使用多项式拟合L1观测值，然后与伪距作差探测不敏感周跳[7]。文献[8]基于模拟的三频信号研究了三频周跳的探测与修复，提出使用多个组合量联合探测并修复周跳，减少了不敏感周跳的影响，并使用LAMBDA搜索周跳真值。文献[9]使用5个组合观测量探测周跳，其中3个混合相位和伪距组合观测量探测大周跳，两个无几何相位组合观测量探测小周跳，减少了不敏感周跳的数量。文献[10]使用优化的组合系数提升周跳探测效果，在一部分无几何组合系数中优选了组合量。

目前基于GF组合的周跳探测方法已经得到了广泛应用，但多个GF组合的不敏感周跳尚不明确。本文从几何关系的角度研究了多个GF组合与MW的探测原理，搜索了相应的不敏感周跳，研究了数据组合的优化方法，并用实测数据检验了优化算法探测并修复周跳的效果。

1 三频周跳探测几何原理

若a、b、c分别为3个频率上相位观测值的系数，则可组成如式(1)所示的组合观测值，组合观测值的噪声如式(2)所示[11]。若系数满足式(3)，该组合观测值为GF组合，GF组合消除了接收机钟差、对流层延迟等误差，是理想的周跳探测量[12]，其历元间残差值进一步减弱了电离层延迟

φc=aφ1+bφ2+cφ3

(1)

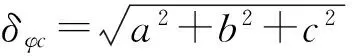
(2)

(3)

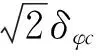
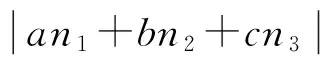
(4)

1.1 不敏感周跳

不能探测的不敏感周跳满足式(5)，将式(2)代入式(5)整理可得式(6)。式(6)包含多个变量和系数，难以使用传统代数方法分析及优化，可在三维坐标系中表示式(6)的几何意义

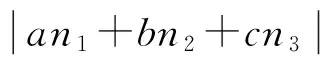
(5)

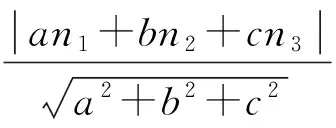
(6)

图1 不敏感周跳分布范围Fig.1 Distribution range of insensitive cycle-slip

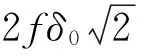
2 数据组合的选取

一个GF组合无法解算3个频点上的周跳值，且不敏感周跳总量较多，因此可使用多个组合量相互探测不敏感周跳，并解算3个频点的周跳值。

2.1 两个GF组合

使用两个GF组合探测周跳，只要其中一个GF组合探测到周跳，便判断为周跳。若两个GF组合分别为(a1,b1,c1)和(a2,b2,c2)，则两个GF组合不能探测的周跳满足式(7)

(7)

式(7)等价于两个式(5)并列，其几何原理如图2(a)所示，平面α1和α2之间的整数节点为(a1,b1,c1)的不敏感周跳，平面β1和β2之间的整数节点为(a2,b2,c2)的不敏感周跳，则其公共的不敏感周跳为α1、α2、β1和β24个平面所围成的空间内的整数节点，围成的空间是一个无限长的四棱柱，如图2(b)所示。四棱柱的长度是无穷大，因此两个GF组合不敏感周跳数量也是无穷大，但与一个GF组合相比，两个GF组合不敏感周跳数量是低阶的无穷大，因此两个GF组合将显著减少不敏感周跳的数量。

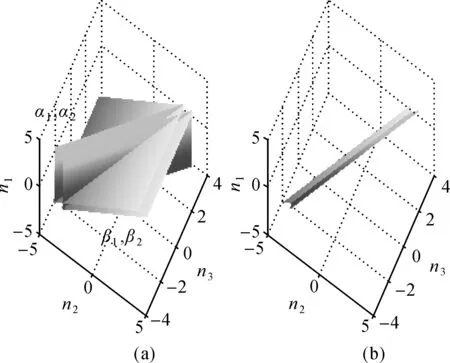
图2 两个GF组合探测周跳原理Fig.2 Principle of detection based on 2 GF

2.2MW组合

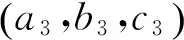
(8)

式中，δMW为MW组合的中误差，由于使用了伪距测量值，数值较大。在两个GF组合的基础上增加MW组合，等价于在图2(b)中增加两个互相平行的平面截断四棱柱，如图3所示，平面γ1和γ2之间的整数节点为MW组合的不敏感周跳，截断的四棱柱体积不再是无穷大，因此增加MW组合与两个GF组合可将不敏感周跳数量控制在有限数量内，显著减少了不敏感周跳。

图3 两个GF与MW组合联合探测周跳Fig.3 Detection of 2 GF and MW combinations

3 优化方法

3.1 系数优化

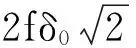
图4 两个GF组合对应的四棱柱横截面Fig.4 Cross section of the four prism for 2 GF

(9)

(10)

最优的GF组合系数应使S取最小值。式(10)中，S为一元函数，当θ=90°时，有最小值Smin=0.029，此时平面α1与β1的法向量相互垂直，即系数满足式(11)

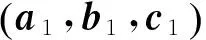
(11)

将式(11)与式(3)联立可解得最优的组合系数，但3个方程解6个系数有无限解，因此本文随机求取一个解进行试验。随机令a1=b1=1，再由式(3)求得c1，得到第一个GF组合量(1,1,-2.182 258)，将该系数代入式(10)并联立式(3)解算第2个GF系数，随机令a2=1可得到第2个GF组合(1,-1.165 912,-0.121 147) 。

3.2 多个GF组合的必要性

三频组合观测值中，线性独立的无几何相位组合只有两组，因此第3个及以上的GF组合不能独立讨论。若将式(3)代入平面方程an1+bn2+cn3=0，可得到一个直线方程式(12)，这个直线方程与组合系数无关，因此所有的GF组合系数所对应的平面an1+bn2+cn3=0都经过该直线，图2(b)中四棱柱的中心线就是该直线

n1λ1=n2λ2=n3λ3

(12)

在两个优化的GF组合上增加第3个GF组合，等价于在图4中再加入两个与四棱柱中心线平行的平面，如图5所示，增加的GF组合将横截面切为六边形，横截面积有所减少。但增加的GF无法减少图5中内切圆面积，内切圆的面积与正方形面积之比为π/4，因此再增加GF组合最多能减少的21.5%的不敏感周跳。过多的GF组合会增加计算量，因此本文使用2个优化的GF组合和MW组合探测并修复周跳。

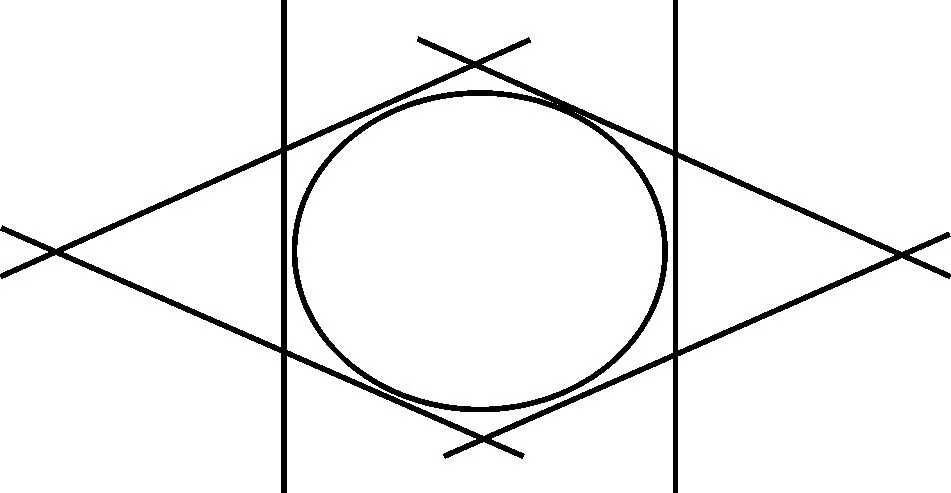
图5 增加第3个GF组合后的横截面积变化Fig.5 Variation of cross-sectional area after adding the third GF

4 周跳修复

周跳修复是指求出周跳在3个频点上的跳变量，然后在后续历元的相位观测值中减去该跳变量[16]。周跳修复和整周模糊度固定原理相似：①估计周跳浮点解；②固定周跳整数解。但周跳修复属于数据预处理，修复的结果直接影响到后续定位结果，因此要求高可靠性。周跳修复原理与周跳探测原理是统一的，至少需3个相互独立的组合量才能估计周跳，因此本文选取的两个GF组合和MW组合既可用于探测不敏感周跳，也可用于周跳修复。

若两个GF组合的系数分别为(a1,b1,c1)和(a2,b2,c2)，MW组合中相位观测值的系数为(a3,b3,c3)，则周跳(n1,n2,n3)可由式(13)估计，其中Δφc1和Δφc2分别为两个GF组合的跳变量，ΔMW为MW组合的跳变量

(13)

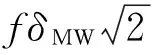
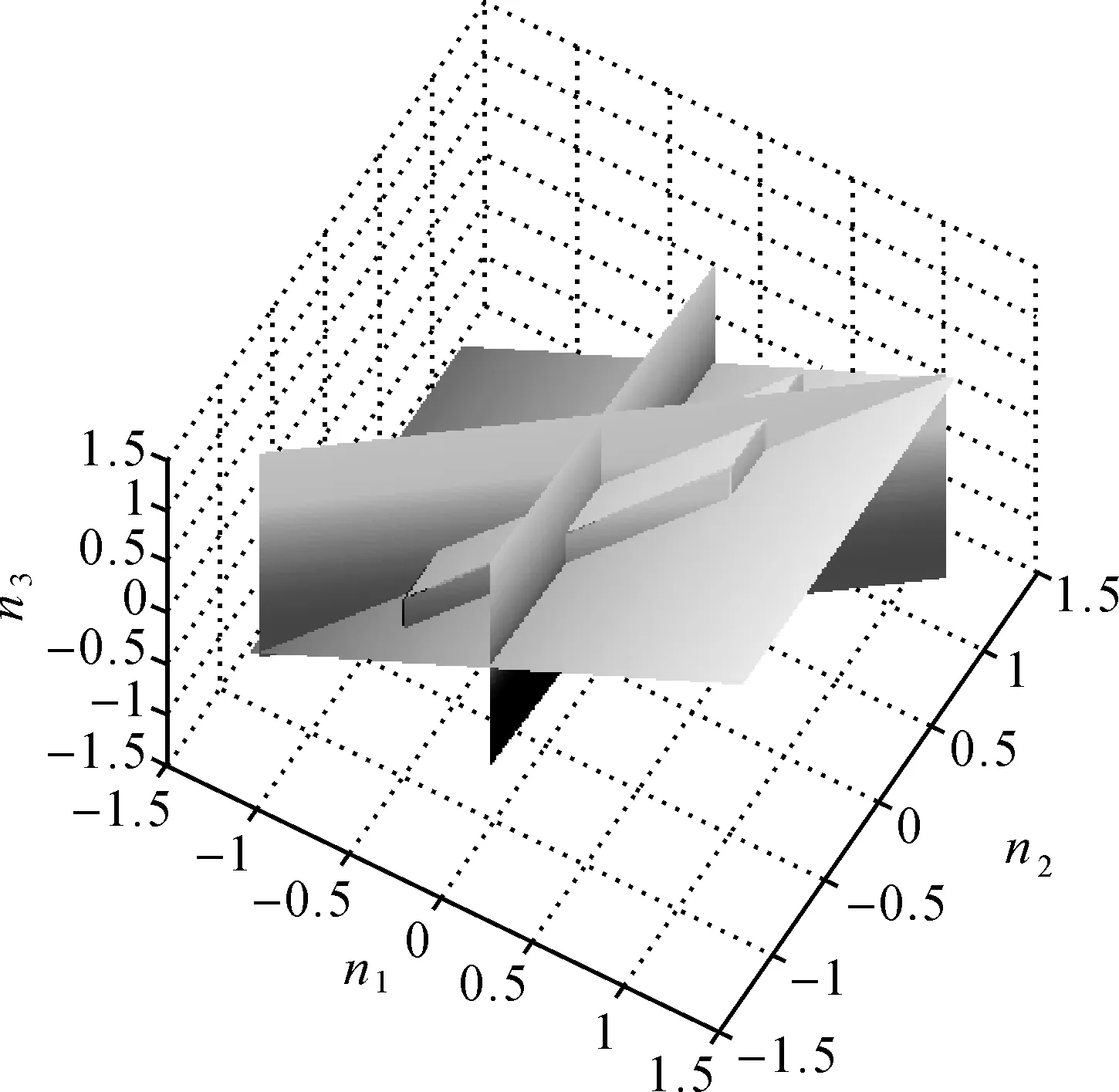
图6 周跳的估计值与真值范围Fig.6 Estimated value and the range of truth-value

5 试 验

本文选取了2016年6月15日的北斗三频静态观测数据进行试验，观测时长为24h，高度截止角15°。由于需要至少625 000个历元的观测值，而观测时段过长无法保持观测环境的一致性，因此使用高采样率0.1s，其中对GEO卫星C01卫星连续观测了24h，共864 000个历元。经GF组合站间双差的方法探测周跳，C01号卫星的观测值不存在“原始周跳”[15]。因此通过编程实现从第5个历元开始每隔5个历元加入一个周跳，依次为(0,0,1)，(0,0,2)，…，(50,50,50)共125 000个周跳。

首先分别使用1个、2个、3个GF组合和LG组合探测周跳，并分别统计未探测到的周跳数量，然后将MW组合加入，再重复上述试验，统计未能探测的周跳数量，使用的组合系数及探测结果列于表1。其中使用2个GF组合和MW组合探测周跳后修复周跳，探测量、估计值和修复值均列于表2。

表1 不敏感周跳数量与使用的组合量

Tab.1 Quantities of insensitive cycle-slip and combinations used

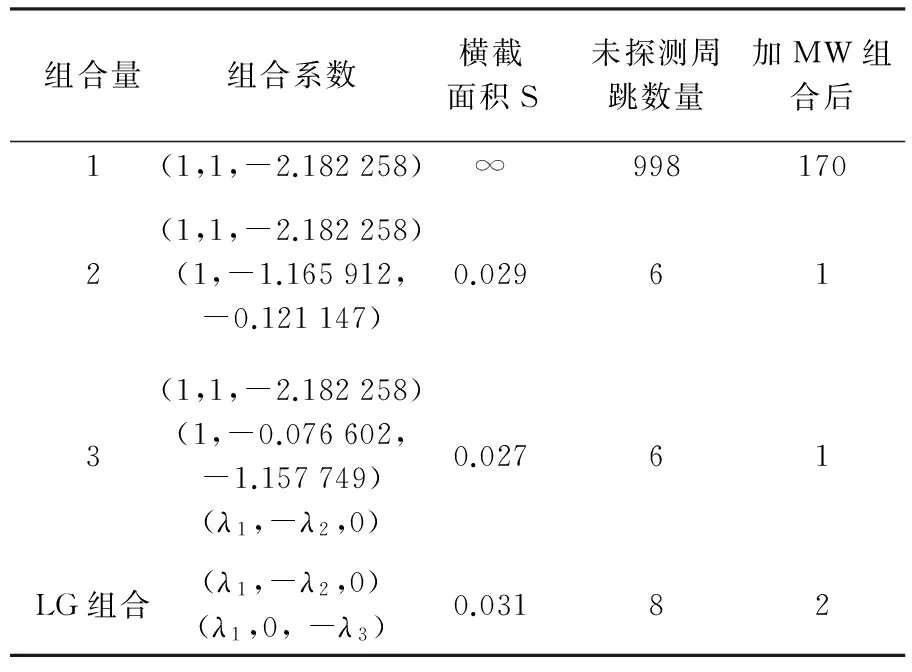
组合量组合系数横截面积S未探测周跳数量加MW组合后1(1,1,-2.182258)∞9981702(1,1,-2.182258)(1,-1.165912,-0.121147)0.029613(1,1,-2.182258)(1,-0.076602,-1.157749)(λ1,-λ2,0)0.02761LG组合(λ1,-λ2,0)(λ1,0,-λ3)0.03182

将表1中未探测到的周跳数量与GF组合数量整理成图7。图中一个GF组合的不敏感周跳数量为998个，加入MW组合后减少为170个，可见不敏感周跳的数目较多，探测效果不理想；而两个GF组合的不敏感周跳仅6个，加入MW组合后仅1个，显著减少了不敏感周跳的数量；当GF组合数量为3时，不敏感周跳与两个GF组合相同，虽然3个GF组合的横截面积比2个最优GF组合的横截面积减少了0.002(7%)，但减少的空间中没有包含整数节点，因此不敏感周跳的数量没有变化。

表2 MW组合和2个GF组合修复周跳结果

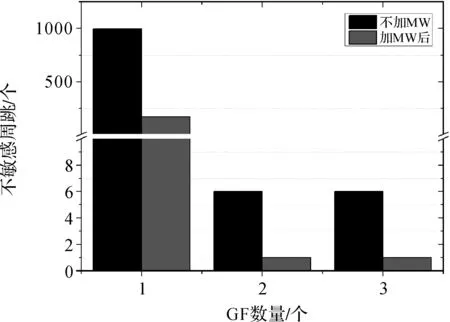
图7 GF数量与不敏感周跳Fig.7 Insensitive cycle-slip and GF quantities

将表1中优化的GF组合与LG组合探测结果整理成图8，在不加MW组合的情况下，优化GF组合有6个不敏感周跳，而LG组合为8个，这一结果与两者对应横截面积之比一致，一方面验证了优化方法的有效性，另一方面表明传统的LG组合的几何构型也较好。加入MW组合后，LG组合有2个不敏感周跳，而优化的GF组合仅一个不敏感周跳(5,4,4)，表明MW组合进一步减少了不敏感周跳数量。由于坐标(5,4,4)位于图3中被截断的四棱柱内，因此对GF组合和MW组合均不敏感，周跳(5,4,3)、(5,4,4)和(5,4,5)的检测序列如图8所示，其中周跳(5,4,3)和(5,4,5)的跳变量明显超出阈值，而(5,4,4)的跳变量很小，见图9。

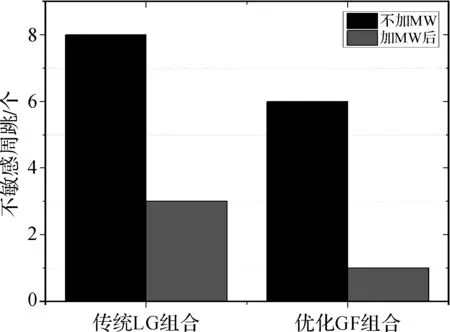
图8 优化的GF组合与LG组合的不敏感周跳Fig.8 Insensitive cycle-slip of optimized GF combinations and LG combinations

在表2中，周跳估计值与修复值的偏差均小于1，表明式(13)估计的周跳值较准确，解决了方程组病态问题。此外，修复值不存在多个整数解及没有整数解的情况，是搜索空间中满足条件的唯一坐标点，这是因为周跳修复中阈值系数f设为1倍中误差，而周跳探测中f设为5倍中误差，所以周跳探测中会有不敏感周跳，而周跳修复中搜索到的整数解具备唯一性。

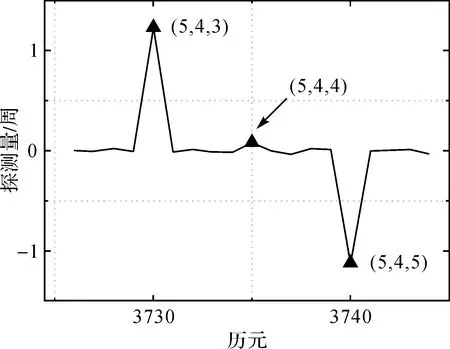
图9 不敏感周跳(5,4,4)的探测序列Fig.9 Experiment data of insensitive cycle-slip (5,4,4)

6 结 语

本文研究了三频周跳探测与修复的几何原理，以及多个GF组合和MW组合探测周跳时的不敏感周跳，最后使用北斗三频实测数据验证了相关结论，对GPS亦适用，试验中0.1 s的高采样率使得各历元观测环境保持一致，但也减弱了电离层延迟的影响，因此在30 s采样率下重复了该试验，与0.1 s采样率下的试验结果相同，这是因为采用了5倍中误差作为阈值(传统方法采用3倍中误差)，可适用较复杂的观测条件。本文提出的周跳探测方法同样适用于接收机动态运动情况，因为使用的无几何组合消除了几何距离项，但周跳修复方法存在无法找到整数解的情况，这是因为实际产生的周跳存在不为整数的情况，这与接收机质量有关，例如部分接收机信号失锁后可能并没有立即停止整周计数，关于非整周跳变的产生原因尚有待研究，但非整周跳变的修复精度难以保证，因此修复非整周跳变是不可靠的。本文提出的方法对于非整周跳变不予修复，保证了修复后数据的可靠性。

(1) GF组合的不敏感周跳总量与阈值成正比，与系数无关，但不敏感周跳在三维坐标系中的坐标随系数变化而变化，因此可用多个GF组合联合探测不敏感周跳，提升周跳探测的可靠性。

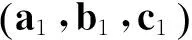
(3) 增加MW组合与2个GF组合联合探测周跳可将不敏感周跳数量控制在有限范围内，本文优化的两个GF组合增加MW组合后仅一个不敏感周跳(5,4,4)，若要完全消除不敏感周跳的影响，则MW组合使用的伪距需是精码。

(4) 增加MW组合与2个GF组合可完成三频周跳的修复，周跳估计值较准确，以步长为3搜索整数解时，不存在多个整数解或未搜索到整数解现象，验证了选取的GF组合和MW组合的合理性，因而解算周跳时不存在病态性问题。

[1] 李金龙, 杨元喜, 徐君毅, 等. 基于伪距相位组合实时探测与修复GNSS三频非差观测数据周跳[J]. 测绘学报, 2011, 40(6): 717-729.LIJinglong,YANGYuanxi,XUJunyi,etal.Real-timeCycle-slipDetectionandRepairBasedonCode-phaseCombinationsforGNSSTriple-frequencyUn-differencedObservations[J].ActaGeodaeticaetCartographicaSinica, 2011, 40(6): 717-729.

[2] 张成军, 许其凤, 李作虎. 对伪距/相位组合量探测与修复周跳算法的改进[J]. 测绘学报, 2009, 38(5): 402-407. DOI: 10.3321/j.issn:1001-1595.2009.05.005. ZHANG Chengjun, XU Qifeng, LI Zuohu. Improving Method of Cycle Slip Detection and Correction Based on Combination of GPS Pseudo Range and Carrier Phase Observations[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(5): 402-407. DOI: 10.3321/j.issn:1001-1595.2009.05.005.

[3] 范建军, 王飞雪, 郭桂蓉. GPS三频非差观测数据周跳的自动探测与改正研究[J]. 测绘科学, 2006, 31(5): 24-26, 36. FAN Jianjun, WANG Feixue, GUO Guirong. Automated Cycle-slip Detection and Correction for GPS Triple-frequency Undifferenced Observables[J]. Science of Surveying and Mapping, 2006, 31(5): 24-26, 36.

[4] 刘胜男, 黄张裕, 彭磊, 等. 利用三频组合观测值的GPS周跳探测与修复[J]. 测绘科学, 2012, 37(5): 46-48. LIU Shengnan, HUANG Zhangyu, PENG Lei, et al. GPS Cycle-slip Detection and Repairing Using Triple-frequency Combination Observations[J]. Science of Surveying and Mapping, 2012, 37(5): 46-48.

[5] ZHANG Xiaohong, LI PAN. Benefits of the Third Frequency Signal on Cycle Slip Correction[J]. GPS Solutions, 2016, 20(3): 451-461.

[6] DAI Zhen. MATLAB Software for GPS Cycle-slip Processing[J]. GPS Solutions, 2012, 16(2): 267-272.

[7] BLEWITT G. An Automatic Editing Algorithm for GPS Data[J]. Geophysical Research Letters, 1990, 17(3): 199-202.

[8] DAI Zhen, KNEDLIK S, LOFFELD O. Instantaneous Triple-frequency GPS Cycle-slip Detection and Repair[J]. International Journal of Navigation and Observation, 2009, 2009: 407231.

[9] DE LACY M C, REGUZZONI M, SANSò F. Real-time Cycle Slip Detection in Triple-frequency GNSS[J]. GPS Solutions, 2012, 16(3): 353-362.

[10] HUANG Lingyong, LU Zhiping, ZHAI Guojun, et al. A New Triple-frequency Cycle Slip Detecting Algorithm Validated with BDS Data[J]. GPS Solutions, 2016, 20(4): 761-769.

[11] 张小红, 何锡扬. 北斗三频相位观测值线性组合模型及特性研究[J]. 中国科学: 地球科学, 2015, 45(5): 601-610. ZHANG Xiaohong, HE Xiyang. BDS Triple-frequency Carrier-phase Linear Combination Models and Their Charac-teristics[J]. Science China Earth Sciences, 2015, 58(6): 896-905.

[12] 黄令勇, 翟国君, 欧阳永忠, 等. 三频GNSS电离层周跳处理[J]. 测绘学报, 2015, 44(7): 717-725. DOI: 10.11947/j.AGCS.2015.20140348. HUANG Lingyong, ZHAI Guojun, OUYANG Yongzhong, et al. Ionospheric Cycle Slip Processing in Triple-frequency GNSS[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 717-725. DOI: 10.11947/j.AGCS.2015.20140348.

[13] 熊伟, 伍岳, 孙振冰, 等. 多频数据组合在周跳探测和修复上的应用[J]. 武汉大学学报(信息科学版), 2007, 32(4): 319-322. XIONG Wei, WU Yue, SUN Zhenbing, et al. Application of Multi-frequency Combination Observation in Cycle Slip Detection and Restoration[J]. Geomatics and Information Science of Wuhan University, 2007, 32(4): 319-322.

[14] 段荣, 赵修斌, 庞春雷, 等. 一种基于TurboEdit改进的GPS周跳探测与修复方法[J]. 仪器仪表学报, 2015, 36(11): 2487-2494. DUAN Rong, ZHAO Xiubin, PANG Chunlei, et al. Improved Cycle Slip Detection and Repair Method for GPS Receiver Based on TurboEdit Algorithm[J]. Chinese Journal of Scientific Instrument, 2015, 36(11): 2487-2494.

[15] CHEN D, YE S, ZHOU W, et al. A Double-differenced Cycle Slip Detection and Repair Method for GNSS CORS Network[J]. GPS Solutions, 2016, 20(3): 439-450.

[16] ZHAO Qile, SUN Binzi, DAI Zhiqiang, et al. Real-time Detection and Repair of Cycle Slips in Triple-frequency GNSS Measurements[J]. GPS Solutions, 2015, 19(3): 381-391.

(责任编辑：陈品馨)

Real-time Cycle-slip Detection and Repair Algorithm of GNSS Triple-frequency Observations

LIU Liu1,2,LÜ Zhiwei1,2,YU Xiaodong3,WANG Pengxu1,2,YANG Dongsen1,2，ZHANG Lundong1,2,CONG Dianwei1,2

1. University of Information Engineering, Zhengzhou 450001, China； 2. BeiDou Navigation Technology Collaborative Innovation Center of Henan, Zhengzhou 450001, China; 3. SinoGNSS Technology Ltd, Shanghai 201801, China

Method of cycle-slip detection based on Geometry-free observation combinations has insensitive cycle-slip. This paper analyzes the principle of cycle-slip detection based on the geometric relationship. Then study the similarities and differences of more than one geometry free phase combinations separately. And study the effect of adding a MW(Melbourne Wübbena) combination. We proposed to select GF(Geometry Free) combinations by cross-sectional area. Finally BeiDou triple-frequency data have been used to validate the conclusion. We conclude that two geometry-free phase combination is the most reasonable choice for the detection of insensitive cycle-slip. And a MW combination can obviously decrease the amounts of insensitive cycle-slip. The optimized algorithm only has 1 insensitive cycle slip, and all detected cycle-slip repaired successfully.

cycle-slip detection; insensitive cycle-slip; cycle-slip repair; optimization of coefficients; phase geometry-free combinations

The National Natural Science Foundation of China (Nos. U1636219；41604032); The National Key Research Plan Project Funding(No.2016YB0801303)；Geographic Information Engineering National Key Laboratory of Open Research Fund (No.SKLGIE2015-M-2-5)

LIU Liu(1992—)，male，postgraduate，majors in satellite navigation.

刘柳，吕志伟，于晓东，等.GNSS三频周跳探测与修复算法[J].测绘学报，2017,46(4)：453-459.

10.11947/j.AGCS.2017.20160532. LIU Liu, LÜ Zhiwei,YU Xiaodong,et al.Real-time Cycle-slip Detection and Repair Algorithm of GNSS Triple-frequency Observations[J]. Acta Geodaetica et Cartographica Sinica,2017,46(4):453-459. DOI:10.11947/j.AGCS.2017.20160532.

P228.4

A

1001-1595(2017)04-0453-07

国家自然科学基金(U1636219;41604032); 国家重点研发计划(2016YB0801303)；地理信息工程国家重点实验室开放研究基金(SKLGIE2015-M-2-5)

2016-11-01

刘柳(1992—)，男，硕士生，研究方向为卫星导航。

E-mail： whull@whu.edu.cn

修回日期： 2017-03-12