北斗卫星超短弧运动学定轨方法优化与试验分析

郭 睿，陈金平，朱陵凤，唐桂芬，吴晓莉

1. 北京卫星导航中心, 北京 100094； 2. 大地测量与地球动力学国家重点实验室，湖北 武汉 430077



北斗卫星超短弧运动学定轨方法优化与试验分析

郭 睿1,2，陈金平1，朱陵凤1，唐桂芬1，吴晓莉1

1. 北京卫星导航中心, 北京 100094； 2. 大地测量与地球动力学国家重点实验室，湖北 武汉 430077

针对北斗卫星姿轨控后的轨道快速确定难题，系统地研究了基于多项式拟合和基于星历拟合两种运动学定轨方法，推导建立了相应的运动学定轨模型。同时针对接收机系统差和顽固多径问题，利用基于并置比对的接收机系统差解算方法和CNMC的多径削弱方法，实现了超短弧跟踪条件下接收机数据质量的有效控制。利用北斗GEO/IGSO/MEO卫星的实测伪距数据进行了试验验证，结果表明在10 min超短弧跟踪条件下，GEO、IGSO和MEO卫星的运动学定轨位置精度分别为3.27 m、8.19 m和5.90 m，实现了超短弧跟踪条件下的北斗卫星快速定轨，满足了卫星机动期间的北斗RDSS服务对轨道精度的需求，为北斗RDSS服务走向全球提供了技术支撑。

北斗卫星导航系统；精密定轨；轨道机动；运动学法定轨；多径误差

北斗卫星导航系统(BDS)作为全球四大卫星导航系统之一，于2012年12月27日正式开始运行，主要为中国及周边地区提供定位、授时和短报文服务[1]，首次同时实现了无线电定位业务(radio determination satellite service, RDSS)和无线电导航业务(radio navigation satellite service, RNSS)服务。RDSS服务是BDS系统的重要组成和鲜明特色，主要依托在轨5颗GEO(geostationary earth orbit)卫星完成有源服务，具有不间断和强实时性的特点[4]。

在BDS系统中，连续和稳定的卫星精密轨道测定与预报是卫星导航系统服务性能及可用性的重要保证。受地球非球形引力等摄动因素的影响，卫星轨道根数存在长期摄动影响，卫星位置在经度和纬度方向均存在漂移问题。但是受轨位和频率资源的限制，北斗卫星需要定期进行轨道机动。特别是对于轨位资源相对匮乏的GEO卫星，其轨道机动的频度更高，部分卫星的机动周期达到25 d左右[7]。

实时、不间断的现代导航服务需求对导航系统的运行控制能力提出了新的更高要求，传统的精密定轨理论难以处理卫星姿轨控期间和姿轨控后的精密轨道确定。

对于GPS系统，当卫星机动后，通常将该卫星从星座中剔除，机动前和机动期间的观测数据将不再参与定轨，卫星将重新积累数据，待卫星定轨状态稳定之后，再重新进行星座组网处理。受地面跟踪几何条件、观测数据量、测量误差和上行注入等诸多因素的影响，在GPS系统地面运控端通常需要重新积累4～6 h的数据后再进行定轨处理，其定轨精度才能恢复到正常水平，因此在轨卫星轨道机动后存在6 h左右的不可用状态。

对于BDS卫星机动期间定轨，文献[10—11]中提出了机动力建模条件下的GEO卫星机动期间定轨方法，但由于跟踪弧段有限，同时卫星在轨机动喷力数据存在误差，基于机动力建模的动力学定轨难以实现米级的卫星轨道测定，其精度大约为50 m。在卫星机动后的恢复期间，文献[9]提出了时间同步约束的快速动力学定轨方法，实现了机动后4 h的轨道快速恢复，其定轨位置精度优于10 m，有效解决了卫星频繁轨道机动后的快速恢复问题。

但是从单颗卫星可用度而言，北斗卫星在机动期间(通常约2 h)与恢复4 h内共6 h左右时间期间，卫星广播星历参数无法达到正常服务水平，机动卫星仍处于不可用状态，北斗RNSS服务存在下降风险。对于北斗RDSS服务，虽然其对卫星轨道精度的要求不高，但从北斗系统整体服务性能来看，仍然存在较大的提升空间。

当卫星进行轨道机动后，笔者前期提出了基于多项式拟合[12]和基于星历拟合[13-14]两种运动学定轨方法，并利用北斗GEO卫星和MEO卫星的实测数据进行了验证。试验结果表明在10 min左右的超短弧条件下，GEO卫星定轨精度约为20 m[13]，MEO卫星定轨精度约为8 m[14]。受伪距多径和接收机系统差等因素的制约，该定轨方法存在一定的优化空间。同时需要对两种运动学定轨方法在北斗GEO/IGSO/MEO混合星座的应用特性进行系统性分析，特别是超短弧条件下的轨道预报能力论证，有助于北斗卫星精密定轨体制的确立与优化。

本文立足北斗卫星超短弧跟踪条件下的快速轨道确定问题，系统地研究了基于多项式拟合和基于星历拟合两种超短弧运动学定轨方法，采用CNMC(code noise and multipath correction)算法的多径削弱技术和基于并置比对的接收机系统差解算技术，有效实现了北斗机动卫星测轨数据质量控制，并利用北斗3种不同类型的卫星实测数据进行了定轨试验验证，完成了北斗卫星运动学定轨的系统论证，得到了一些有益结论，其中北斗GEO卫星超短弧条件下的定轨精度得到大幅提升。

1 超短弧运动学定轨方法

超短弧运动学定轨方法主要有两种，其一是基于多项式拟合的运动学定轨，其二是基于星历拟合的运动学定轨。下面对两种方法进行简要介绍。

1.1 基于多项式拟合的运动学定轨模型

在短弧跟踪条件下，采用单点定位只能得到一系列时间连续但不光滑的卫星位置，而无法直接获得卫星速度。当跟踪弧段很短时，卫星运动轨道是平滑的，因此可以利用1个n阶多项式来近似地描述卫星的地固系位置，建立基于多项式拟合的短弧运动学法定轨模型，利用多项式与卫星位置或星地距离之间的模型关系，对多项式系数进行估计，实现超短弧运动学定轨。当m个地面跟踪站实现站间时间同步的前提下同时对卫星进行跟踪，其观测模型如式(1)所示

(1)

式中，ρ(j,t)表示t时刻第j个跟踪站观测的伪距；(Xt,Yt,Zt)表示t时间卫星的地固系位置；(Xsj,Ysj,Zsj)表示第j个跟踪站的地固系位置；Ai(i=1,…,n)为卫星X方向多项式系数；Bi(i=1,…,n)为卫星Y方向多项式系数；Ci(i=1,…,n)为卫星Z方向多项式系数；τ表示t时刻的卫星钟差。对观测方程进行线性化处理，可以构建相应的误差方程，依据最小二乘法解算待估参数[A0,A1,…,An,B0,B1,…,Bn,C0,C1,…,Cn,τ]；当卫星钟差通过其他手段(如卫星双向频率传递)测定后，卫星钟差参数τ可以不需要估计，定轨解算的DOP(dilution of precision)值将得到较大改善。在具体的实现过程中，可以采用基于单点定位的多项式拟合法和基于伪距的多项式拟合法，详细原理参考文献[12]。为了提高定轨精度，本文主要采用基于伪距的多项式拟合法，即直接建立多项式与原始伪距观测之间的数学关系。

1.2 基于星历拟合的运动学定轨模型

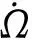
在上述16参数的广播星历模型中，toe和6个开普勒轨道参数在描述卫星轨道中是必需的，3个一阶摄动参数能够反映重要轨道参数的一阶变化率，而6个调和摄动参数主要反映了各种类型的轨道摄动。由于调和改正项主要与卫星轨道周期相关，在超短弧条件下这6个参数估计结果严重失真。

2 数据质量控制

接收机观测数据质量是北斗卫星运动学定轨精度的重要保证。受卫星星座和观测环境等因素的制约，北斗卫星伪距观测数据中存在较严重多径问题(特别是GEO卫星)[15-16]，同时接收机时延也存在一定的系统差偏差，并且随着在轨运行存在长期漂移的问题。下面主要针对接收机系统差和伪距多径问题，研究和设计接收机数据质量控制方法。

2.1 基于并置比对的接收机系统差标校方法

接收机通道时延存在标定误差，同时设备在轨运行存在时延长期漂移的问题。在超短弧跟踪条件下，由于观测数据少，测站和卫星设备系统差难以建模，直接估计将导致定轨不收敛，因此接收机系统差的精确标校是制约超短弧运动学定轨的关键问题。

对于同一测站而言，为了保证地面系统运行的可靠性，通常安装2—3台接收机进行相互备份。接收机通常有外频标和内频标驱动共两种工作模式，在地面处理系统通常是采用外频标驱动，所有接收机均采用相同的外部时频系统进行驱动。接收机系统差主要包括不同频率间相对硬件延迟和相对于外频标1 pps的绝对硬件延迟两部分。对于相对硬件延迟，可以通过选取夜间背景场和适当的约束条件进行解算，其精度可以优于1 ns[17]。对于绝对硬件延迟，主要由接收机厂家在出厂前进行标定，但由于标定误差和长期漂移，存在较大误差，需要对其进行标校与解算。

在地面处理系统中，通常会在选择一台基准接收机作为参考基准，进行各类型业务处理，如精密定轨和差分完好性处理，并基于该基准接收机完成各测站接收机之间的时间同步。而基准接收机的时延主要通过高精度时延测量仪器测量得到，其长期变化量主要通过专门的监测设备进行测量，同时配合系统差解算方法进行整网平差。在进行超短弧条件下定轨中需要高精度站钟差的支持，需要将实际使用的定轨接收机与基准接收机进行时延标校，实现两台接收机之间的高精度时间同步。

在同一测站可以选取基准接收机作为参考基准，利用O-C并置比对的方法完成其他接收机的绝对时延标校。其主要原理如下

(2)

式中，R1、R2分别为接收机1和2的理论星地距离；ρ1和ρ2分别为接收机1和2的下行伪距观测值；δts为卫星钟差；δtk为测站钟差；ΔDtrop和ΔDion分别为对流层和电离层延迟误差；ΔDrel为广义相对论改正；ΔDtide为地球潮汐改正；ΔDSatTran为卫星发射时延；τ21为接收机2的绝对硬件延迟；ε1和ε2分别为接收机1和2偶然误差。通过计算两个接收机O-C之差，可以完成接收机2绝对硬件延迟的解算与标校。

表1给出北京和海南两个测站的接收机系统差多天解算结果，两站均选取1号机作为参考基准，对2号和3号机进行系统差解算与标校。从结果中可以看出，与基准接收机相比较，不同接收机系统差大约为10～20 ns量级，单台接收机多天的一致性较好，该误差对运动学定轨精度的将达到数十米。不同接收机系统差平均RMS优于1 ns，综合多台接收机系统差解算结果，平均标准差为0.6 ns，因此可以认为基于并置比对的接收机系统差解算精度优于1 ns，可以有效削弱系统差对短弧运动学定轨的影响。

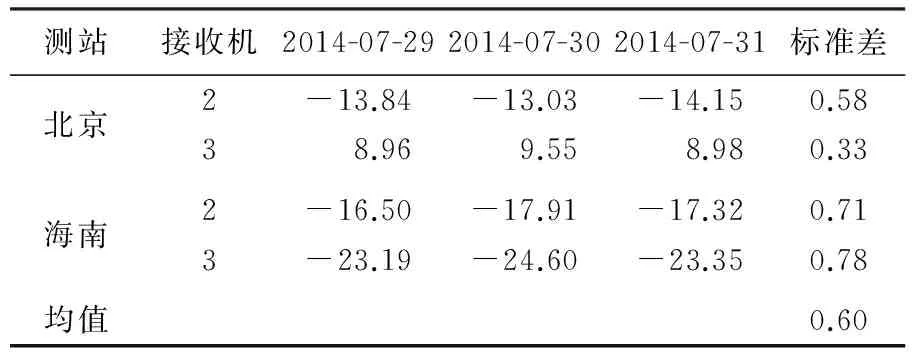
表1 接收机系统差标校结果

对于不同测站接收机系统偏差标校问题，如果异站接收机与基准接收机之间直接采用O-C并置比对法，难以消除公共的传播路径误差。同时，由于两个接收机不是同源时频信号驱动，异站接收机时延与本地钟差是耦合的，难以直接分离。因此，对于异站接收机系统差的标校，直接采用载波共视法或多星定轨法完成测站钟差的估计。

2.2 基于CNMC的多径削弱方法

WAAS(wide area augmentation system)系统提出一种采用CMC(code-minus-carrier)观测量来改正GPS伪距观测多路径效应的方法[18-19],有效改善了WAAS伪距观测量的精度。北斗导航系统采用GEO/IGSO/MEO混合星座设计，基于地面监测站的实测数据分析表明，GEO和IGSO卫星伪距观测量中包含了明显的多径噪声，且GEO的多径噪声尤为严重[20-21]，部分测站多径接近1 m。

考虑到载波相位的多径噪声不超过3 cm，比伪距多径噪声小两个数量级，文献[22]根据伪距和双频载波相位的组合提取伪距观测量中多径噪声，并提出伪距多径噪声改正的实时算法CNMC。该算法原理是利用双频相位组合计算每个历元的电离层延迟，实现平滑单频点伪距观测的目的。该方法消除伪距多径误差的效果显著,定位解算精度改善[23-24]。

下面选取国内分布的7台接收机对北斗GEO和IGSO卫星实测数据，进行CNMC前后的多径对比试验，表2给出了多径RMS统计对比结果。

从表中可以看出CNMC算法多径改正效果明显，其中GEO卫星伪距多径改善率达到60.17%，IGSO卫星伪距多径改善率达到39.54%，GEO卫星的改善效果更加明显。基于CNMC的多径削弱方法，可以对接收机的伪距观测质量进行有效控制，有利于提升超短弧跟踪条件下的运动学定轨精度。

表2 CNMC算法处理前后各星伪距观测量中的多径RMS

3 定轨试验与分析

上文提出了两种运动学定轨方法和接收机数据质量控制方法，并详细推导了具体实现过程。两种运动学方法充分利用了高采样率的测轨数据，减少了结果的噪声，其优点在于不需要累积长期测轨数据，可以实现近实时快速计算，克服了动力学法定轨发散和单点定位无法获取速度信息的不足，实现了短弧跟踪条件下的卫星精密定轨。下面利用北斗系统GEO/IGSO/MEO卫星的实测伪距观测数据，对两种定轨方法进行试验验证。

3.1 定轨方案与评估方法

为了验证两种超短弧运动学定轨方法的精度，采用北斗系统7个测站CNMC修正后的伪距数据进行定轨试验，各测站之间通过所有在轨卫星多星联合定轨实现站间时间同步，各接收机的系统差基于2.1节的并置比对法完成了标校与修正，卫星钟差采用双向时间频率法测定的历元钟差值[25]-[27]。主要定轨处理策略如表3所示。

表3 超短弧运动学定轨处理策略

由于卫星机动期间的定轨精度有限，为了评估多星多站条件下的机动定轨精度，采用非机动期间的数据进行定轨处理，利用长弧多星定轨的轨道产品作为评估标准，统计卫星R、T、N 3个方向和位置误差，表4给出了多星定轨精度的统计结果。从结果中可以看出，多星定轨的平均位置精度为1.28 m，能够评估米级的超短弧运动学定轨精度。

表4 多星定轨精度统计(3 d定轨，重迭1 d)

Tab.4 Multi-satellite precise orbit determination accuracy (3 days tracking arc, 1 day overlap) m

3.2 定轨精度

下面采用2014年8月3日至4日C02(GEO)、C09(IGSO)和C11(MEO)卫星的实测数据进行定轨试验，每颗卫星分别采用2～3个弧段数据进行定轨，每个弧段10 min，定轨方法分别为基于多项式拟合的运动学定轨和基于星历拟合的运动学定轨。在基于多项式拟合的运动学定轨中，由于观测数据只有10 min，同时考虑到待估参数的相关性和轨道预报精度的衰减，多项式的阶数选择为2阶。

将定轨结果与多星定轨结果进行比较，统计两个弧段R、T、N 3个方向和URE的误差均值，同时为了进行结果比较，增加了单点定位结果的精度评估，试验结果统计如表5所示。

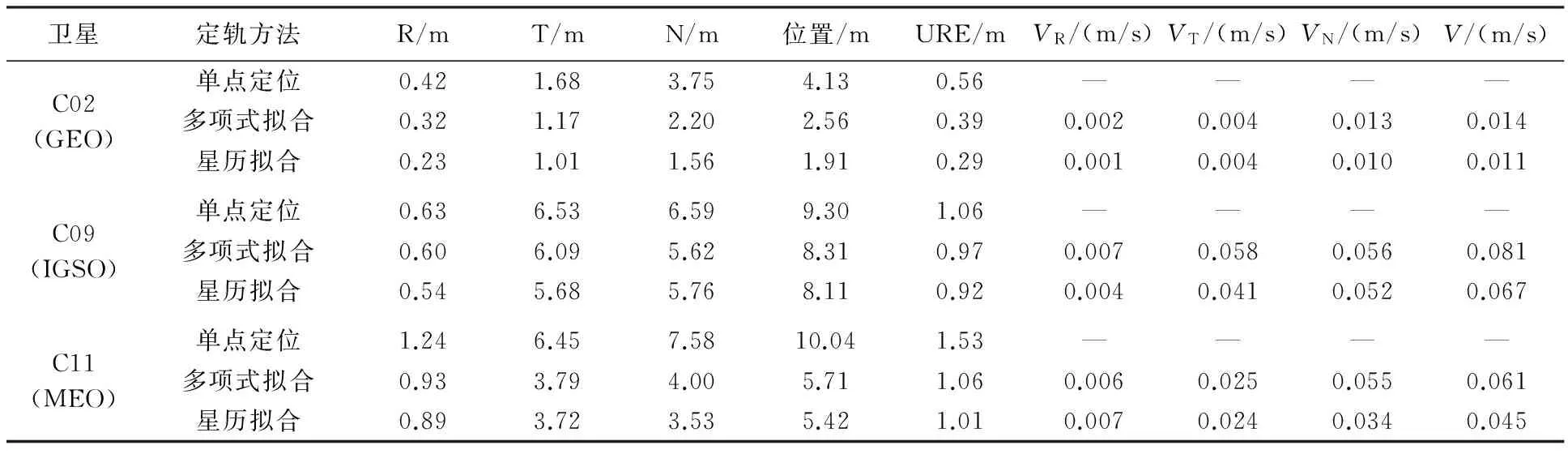
表5 不同定轨方法的定轨精度-1(10 min弧长)

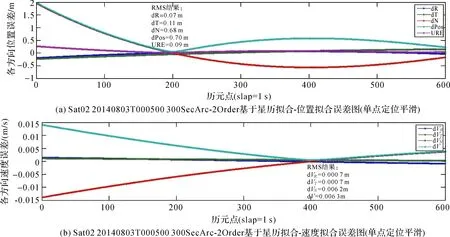
图1 C02卫星基于星历拟合的定轨精度(弧段1)Fig.1 C02 satellite orbit determination accuracy based on ephemeris parameter fitting method (arc 1)

下面对上述运动学定轨精度进行分析：

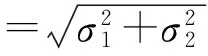
(2) 从不同的定轨方法来看，综合比较3类不同卫星的定轨位置精度，基于星历拟合的超短弧运动学定轨方法精度最高，其次是基于多项式拟合。究其原因，基于星历拟合的定轨方法带有卫星轨道的部分动力学信息，能够更好地描述卫星轨道的物理特性，所以其精度更高。但从位置精度而言，基于多项式拟合的定轨方法同样能够实现卫星轨道的米级定轨精度，满足卫星轨道机动时的RDSS服务所需的卫星星历。

(3) 从不同类型卫星的定轨位置精度来看，GEO卫星虽然高度更高，但其位置精度最好，究其原因是定轨数据预处理中对卫星系统差进行了有效标校，GEO卫星的静地特性使其相对于地球的运动速度小，卫星和测站系统差标校精度高，而且随时间变化缓慢。而IGSO和MEO卫星相对于地球的运动速度更大，测站相对于卫星的多普勒(伪距变化率)大，卫星和测站系统差解算精度更低，随时间变化较快。而卫星和测站系统差通常是采用1d前的标定结果，因此不同类型卫星表现不同的定轨精度。

(4) 从卫星的速度确定精度来看，IGSO和MEO卫星只能获得6cm/s左右的速度精度，GEO卫星可以获得1cm/s左右的速度精度，与IGSO/MEO卫星相比提高5倍，究其原因，GEO卫星相对于地球几乎不动，运动速度小，更有利于速度信息的建模。

(5) 从运动学定轨在北斗系统的应用来看，与传统的机动期间单点定位方法相比，采用运动学定轨方法后轨道精度得到明显改善，提高了1倍左右。特别是GEO卫星，可以实现3.27m左右的定轨精度，由于GEO卫星机动期间需要提供RDSS服务所需的星历，运动学定轨方法能够满足其对GEO卫星轨道精度的需求，从而确保连续的RDSS服务。

(6) 与文献[12—13]中定轨精度相比较，MEO卫星定轨精度相当，而GEO卫星定轨精度得到较大改善，这主要得益于有效的伪距数据质量控制，对接收机系统差和多径误差进行了有效削弱。

为了进一步说明运动学定轨方法的普适性，需要利用更多的卫星进行短弧运动学定轨试验。由于GEO卫星相对于地面跟踪几何条件几乎不变，下面仅利用2014年8月3日C06、C08和C12卫星进行分析，试验方法和条件与前面相同。表6给出了不同方法的统计结果。

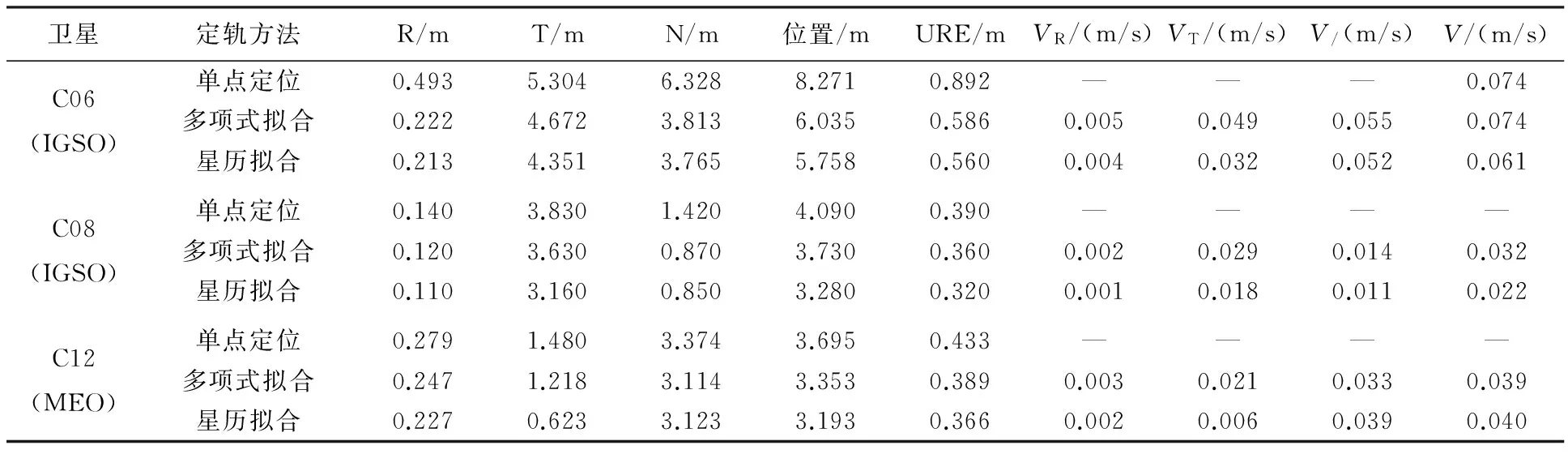
表6 不同定轨方法的定轨精度-2(10 min弧长)

综合表5和表6的结果可以看出，表6中的整体定轨精度优于表5，原因是不同跟踪弧段中卫星相对地面测站的高度角不同。其中表5中各弧段的卫星高度角大约为10°～40°，而表6中卫星高度角在60°左右，因此定轨精度略高。从整体而言，运动学定轨方法对于提高卫星姿轨控期间的定轨精度具有较好的应用价值。

3.3 预报精度

导航用户采用的是卫星预报轨道，因此轨道预报精度非常关键。为了分析两种超短弧运动学定轨方法的预报性能，采用2014年8月3日C02(GEO)、C09(IGSO)和C11(MEO) 3种类型卫星的实测数据进行定轨与预报，定轨弧段为10 min，预报弧段为若干分钟。由于C06、C08和C12卫星几何跟踪条件更好，定轨精度也略高，在此不再进行预报精度分析与统计。下面将定轨结果与多星定轨结果进行比较，统计R、T、N 3个方向和URE的误差，试验结果统计如下。

下面对上述基于多星定轨的运动学轨道预报精度评估结果进行分析：

(1) 对于C02卫星，在10 min左右的超短弧跟踪条件下，综合考虑多星定轨误差和误差传播规律，运动学定轨方法预报10 min的位置精度和URE精度分别优于为7.2 m和1 m，从位置和URE精度来看，机动卫星与非机动卫星的定轨精度相当。因此，从运动学定轨的预报精度来看，能够同时满足北斗RNSS和RDSS服务性能的需求，从而提高单颗GEO卫星的可用度，实现北斗系统可用度的整体提升。

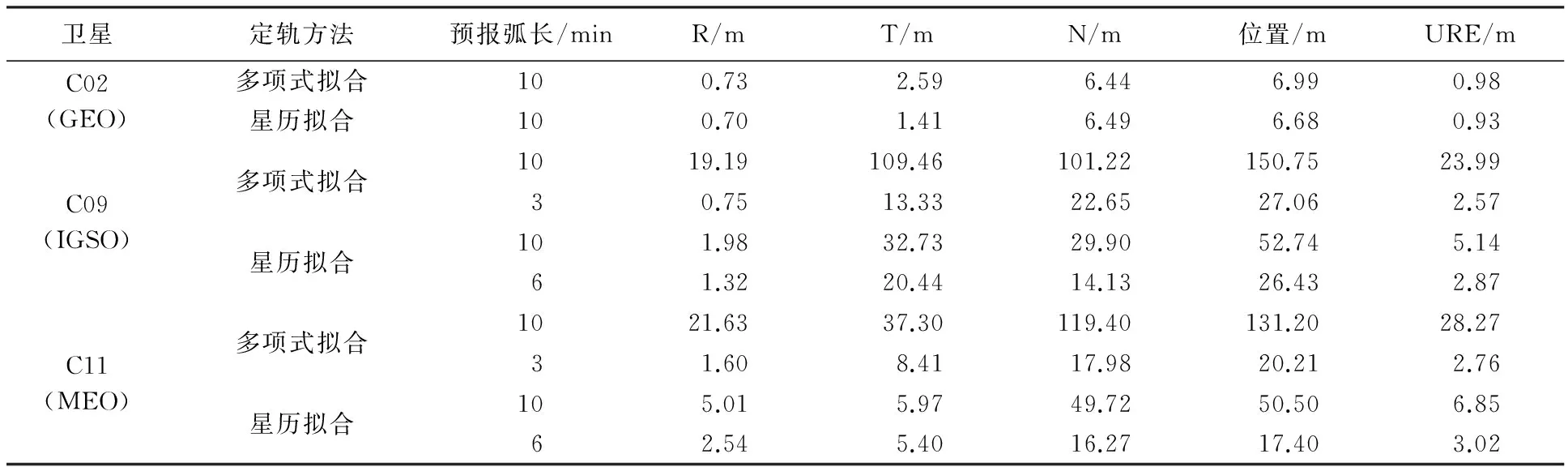
表7 不同定轨方法的预报精度(10 min弧长)

(2) 对于C09和C11卫星，在10 min左右的超短弧跟踪条件下，两种运动学定轨方法预报10 min的轨道位置精度表现了很大差异，其中基于多项式拟合方法达到百米量级，而星历拟合方法为30～50 m精度水平，究其原因，星历拟合方法包含了卫星轨道的部分动力学信息，更加有利于提升轨道的预报能力。

(3) 对比不同类型卫星的轨道预报精度，为了实现优于3 m的URE精度，在10 min的跟踪弧段条件下，GEO卫星能够达到10 min，甚至更长，而IGSO和MEO卫星只能预报3～6 min，其中基于星历拟合法优势更加明显。

(4) 两种运动学定轨方法克服了短弧跟踪条件下动力学法定轨发散问题，同时解决了单点定位不光滑和无法获得卫星速度信息等问题，实现了短弧跟踪条件下的北斗卫星运动学定轨与预报。从预报性能来看，基于星历拟合的运动学定轨方法更加有效，有利于提高轨道的预报能力。

(5) 从北斗系统RDSS服务来看，目前GEO卫星机动期间由于定轨精度不高，轨道预报精度衰减非常快，在线系统通常是1 min左右进行一次几何法定轨和拟合预报，而采用本文提出的运动学定轨方法，不仅提高了卫星定轨和预报精度，而且可以降低系统的处理频度和星历注入频度，降低地面系统的处理强度和负荷，以提升超短弧跟踪条件下RDSS的服务性能。

4 结 论

本文针对北斗卫星姿轨控后超短弧跟踪条件下的轨道快速确定难题，系统地研究了基于多项式拟合和基于星历拟合两种运动学定轨方法，给出了定轨解算模型与实现过程，设计了北斗卫星数据质量控制方法，利用北斗GEO/IGSO/MEO卫星的实测伪距数据进行了定轨试验，主要结论如下：

(1) 两种数据质量控制方法有效削弱了系统差和多径误差对定轨精度的影响，其中基于并置比对的接收机系统差标定精度优于1 ns，GEO和IGSO卫星伪距多径改善率分别达到60.17%和39.54%。

(2) 从定轨位置精度来看，基于多项式拟合和基于星历拟合两种运动学定轨方法是有效的，在10 min跟踪条件下运动学定轨位置精度，GEO、IGSO和MEO卫星定轨精度分别为3.27 m、8.19 m和5.90 m，经过数据质量控制，GEO卫星的运动学定轨精度得到较大改善。

(3) 从定轨速度精度来看，基于星历拟合的定轨方法带有轨道的动力学信息，更好地描述卫星轨道物理特性，其速度精度更高。GEO卫星的静地特性有利于速度建模，IGSO和MEO卫星只能获得6 cm/s左右的速度精度，GEO卫星可以获得1 cm/s左右的速度精度，与IGSO/MEO卫星相比提高5倍。

(4) 从定轨预报精度来看，GEO卫星的超短弧运动学定轨预报10 min能够实现优于7.2 m的轨道位置精度，URE精度优于1 m，其精度水平与非机动卫星相当。在相同条件下为实现优于3 m的URE精度，IGSO和MEO卫星只能预报3～6 min。

(5) 与传统的机动期间定轨方法相比，采用运动学定轨方法后轨道精度得到明显改善，提高了1倍左右，能够有效满足GEO卫星机动期间的RDSS服务对轨道精度的需求，确保北斗RDSS服务连续和稳定。

总之，两种运动学法定轨方法克服了短弧跟踪条件下传统动力学法定轨和单点定位中诸多问题，实现了超短弧条件下的北斗卫星轨道快速确定，能够适用于不同轨道类型的北斗卫星。本文的方法和试验成果能够有效支撑北斗RDSS向全球系统扩展，为北斗RDSS服务走向全球提供技术支撑。

[1] 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1-6. YANG Yuanxi. Progress, Contribution and Challenges of Compass/BeiDou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1-6.

[2] YANG Yuanxi, LI Jinlong, XU Junyi, et al. Contribution of the Compass Satellite Navigation System to Global PNT Users[J]. Chinese Science Bulletin, 2011, 56(26): 2813-2819. DOI: 10.1007/s11434-011-4627-4.

[3] YANG Yuanxi, LI Jinlong, WANG Aibing, et al. Preliminary Assessment of the Navigation and Positioning Performance of BeiDou Regional Navigation Satellite System[J]. Science China Earth Sciences, 2014, 57(1): 144-152. DOI: 10.1007/s11430-013-4769-0.

[4] 谭述森. 广义卫星无线电定位报告原理及其应用价值[J]. 测绘学报, 2009, 38(1): 1-5.DOI:10.3321/j.issn:1001-1595.2009.01.001. TAN Shusen. Theory and Application of Comprehensive RDSS Position and Report[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(1): 1-5.DOI:10.3321/j.issn:1001-1595.2009.01.001.

[5] 谭述森. 卫星导航定位工程[M]. 北京: 国防工业出版社, 2007. TAN Shusen. The Engineering of Satellite Navigation and Positioning[M]. Beijing: The National Defense Industry Press, 2007.

[6] 刘颖, 刘根友, 陈晓峰, 等. 北斗二代卫星导航系统IGSO星增加RDSS功能问题探讨[J]. 大地测量与地球动力学, 2012, 32(3): 72-75. LIU Ying, LIU Genyou, CHEN Xiaofeng, et al. Discussion on Adding RDSS to IGSO Satellite in 2ND Generation BeiDou Navigation Satellite System[J]. Journal of Geodesy and Geodynamics, 2012, 32(3): 72-75.

[7] 黄勇, 胡小工, 黄珹, 等. 利用CAPS测距数据确定GEO卫星变轨期间的轨道[J]. 中国科学 G辑: 物理学 力学 天文学, 2008, 38(12): 1750-1758. HUANG Yong, HU Xiaogong, HUANG Cheng, et al. Precise Orbit Determination of a Maneuvered GEO Satellite Using CAPS Ranging Data[J]. Science in China Series G: Physics, Mechanics and Astronomy, 2009, 52(3): 346-352.

[8] 杨旭海, 李志刚, 冯初刚, 等. GEO卫星机动后的星历快速恢复方法[J]. 中国科学 G辑: 物理学 力学 天文学, 2008, 38(12): 1759-1765. YANG Xuhai, LI Zhigang, FENG Chugang, et al. Methods of Rapid Orbit Forecasting after Maneuvers for Geostationary Satellites[J]. Science in China Series G: Physics, Mechanics and Astronomy, 2009, 52(3): 333-338.

[9] GUO Rui, ZHOU Jianhua, HU Xiaogong, et al. Precise Orbit Determination and Rapid Orbit Recovery Supported by Time Synchronization[J]. Advances in Space Research, 2015, 55(12): 2889-2898. DOI: 10.1016/j.asr.2015.03.001.

[10] 郭睿, 李晓杰, 周建华, 等. 机动力建模条件下的GEO卫星机动期间定轨[J]. 测绘科学技术学报, 2013, 30(5): 465-470. GUO Rui, LI Xiaojie, ZHOU Jianhua, et al. Precise Orbit Determination for the GEO Satellite Maneuver Based on the Thrust Force Model[J]. Journal of Geomatics Science and Technology, 2013, 30(5): 465-470.

[11] 李晓杰, 黄勇, 郭睿, 等. 基于机动力模型的GEO卫星恢复期间定轨[J]. 空间科学学报, 2015, 35(6): 730-737. LI Xiaojie, HUANG Yong, GUO Rui, et al. Orbit Determination Method Based on Thrust Force Model for GEO Satellite in the Period of Orbit Recovery[J]. Chinese Journal of Space Science, 2015, 35(6): 730-737.

[12] 郭睿, 胡小工, 黄勇, 等. 导航卫星的短弧运动学定轨[J]. 飞行器测控学报, 2010, 29(1): 60-67. GUO Rui, HU Xiaogong, HUANG Yong, et al. Navigation Satellite Short-arc Kinematic Orbit Determination[J]. Journal of Spacecraft TT&C Technology, 2010, 29(1): 60-67.

[13] 郭睿, 周建华, 胡小工, 等. 一种地球静止轨道卫星的快速恢复定轨方法[J]. 测绘学报, 2011, 40(S): 19-25, 30. GUO Rui, ZHOU Jianhua, HU Xiaogong, et al. A Strategy of Rapid Orbit Recovery for the Geostaionary Satellite[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S): 19-25, 30.

[14] 郭睿, 胡小工, 黄勇, 等. 基于星历拟合的短弧运动学定轨[J]. 宇航学报, 2010, 31(2): 416-422. GUO Rui, HU Xiaogong, HUANG Yong, et al. Short-arc Kinematic Orbit Determination Based on Ephemeris Fitting[J]. Journal of Astronautics, 2010, 31(2): 416-422.

[15] 冯晓超, 金国平, 范建军, 等. GNSS接收机伪距测量中的多径效应试验分析[J]. 现代电子技术, 2013, 36(5): 77-81. FENG Xiaochao, JIN Guoping, FAN Jianjun, et al. Experimentation and Analysis of Multipath Effect in Pseudo-range Measurement of GNSS Receiver[J]. Modern Electronics Technique, 2013, 36(5): 77-81.

[16] FENG Xiaochao, WU Xiaoli, ZHANG Zhixue, et al. Multipath Mitigation Technique Based on Modifications to GNSS Monitor Station Antennas Field[C]∥Proceedings of China Satellite Navigation Conference (CSNC) 2012. Berlin Heidelberg: Springer, 2012: 655-666.

[17] 吴晓莉, 平劲松, 刘利, 等. 区域卫星导航系统硬件延迟解算[J]. 武汉大学学报(信息科学版), 2011, 36(10): 1218-1221. WU Xiaoli, PING Jinsong, LIU Li, et al. Hardware Delay Solution of Regional Satellite Navigation System[J]. Geomatics and Information Science of Wuhan University, 2011, 36(10): 1218-1221.

[18] SHALLBERG K, SHENG Fang. WAAS Measurement Processing: Current Design and Potential Improvements[C]∥Proceedings of 2008 IEEE/ION Position, Location and Navigation Symposium. Monterey, CA: IEEE, 2008: 253-262.

[19] SCHEMPP T, BURKE J, RUBIN A. WAAS Benefits of GEO Ranging[C]∥Proceedings of the 21st International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2008). Savannah, GA: ION, 2008: 12-15.

[20] WANNINGER L, BEER S. BeiDou Satellite-induced Code Pseudorange Variations: Diagnosis and Therapy[J]. GPS Solutions, 2015, 19(4): 639-648. DOI: 10.1007/s10291-014-0423-3.

[21] HAUSCHILD A, MONTENBRUCK O. A Study on the Dependency of GNSS Pseudorange Biases on Correlator Spacing[J]. GPS Solutions, 2016, 20(2): 159-171. DOI: 10.1007/s10291-014-0426-0.

[22] WU Xiaoli, ZHOU Jianhua, WANG Gang, et al. Multipath Error Detection and Correction for GEO/IGSO Satellites[J]. Science China Physics, Mechanics and Astronomy, 2012, 55(7): 1297-1306.

[23] CAO Yueling, HU Xiaogong, WU Bing, et al. The Wide-area Difference System for the Regional Satellite Navigation System of Compass[J]. Science China Physics, Mechanics and Astronomy, 2012, 55(7): 1307-1315.

[24] 常志巧, 胡小工, 郭睿, 等. CNMC与Hatch滤波方法比较及其在北斗相对定位中的精度分析[J]. 中国科学: 物理学 力学 天文学, 2015, 45(7): 079508. CHANG Zhiqiao, HU Xiaogong, GUO Rui, et al. Comparison between CNMC and Hatch Filter & Its Precision Analysis for BDS Precise Relative Positioning[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2015, 45(7): 079508.

[25] 刘利, 韩春好. 卫星双向时间比对及其误差分析[J]. 天文学进展, 2004, 22(3): 219-226. LIU Li, HAN Chunhao. Two Way Satellite Time Transfer and Its Error Analysis[J]. Progress in Astronomy, 2004, 22(3): 219-226.

[26] 刘利, 韩春好. 地心非旋转坐标系中的TWSTT计算模型[J]. 测绘学院学报, 2004, 21(2): 96-98. LIU Li, HAN Chunhao. Model of TWSTT in the Geocentric Non-rotating Coordinate System[J]. Journal of Institute of Surveying and Mapping, 2004, 21(2): 96-98.

[27] 刘利, 朱陵凤, 韩春好, 等. 星地无线电双向时间比对模型及试验分析[J]. 天文学报, 2009, 50(2): 189-196. LIU Li, ZHU Lingfeng, HAN Chunhao, et al. The Model of Two-way Radio Time Transfer between the Earth and Satellites and Analysis of Its Experiment[J]. Acta Astronomica Sinica, 2009, 50(2): 189-196.

(责任编辑：丛树平)

Kinematic Orbit Determination Method Optimization and Test Analysis for BDS Satellites with Short-arc Tracking Data

GUO Rui1,2,CHEN Jinping1,ZHU Lingfeng1,TANG Guifen1,WU Xiaoli1

1. Beijing Satellite Navigation Center, Beijing 100094, China; 2. State Key Laboratory of Geodesy and Earth’s Dynamics, Wuhan 430077, China

Rapid orbit recovery is a puzzle for the BDS satellites after orbit maneuvers. Two kinematic orbit determination methods are studied, with two orbit determination models being established. The receiver system error and serious multipath error exist in the BDS system. The co-location method is proposed to estimate and calibrate the receiver system errors. A CNMC (code noise and multipath correction) method is introduced to weaken the multipath error. Therefore the data quality is controlled efficiently for the receivers in the short tracking arc. The GEO/IGSO/MEO real data is emploied to carry out tests and validation. Using 10 min short tracking arc, the kinematic precise orbit determination accuracy is about 3.27 m for the GEOs, and 8.19 m for the IGSOs, and 5.9 m for the MEOs. Rapid orbit determination is achieved, which satisfying the orbit requirements from the BDS RDSS services. The kinematic precise orbit determination method also supports the RDSS service walking up to the global world.

BDS; precise orbit determination; orbit maneuver; kinematic precise orbit determination; multipath error

The National Natural Science Foundation of China (Nos. 41204022; 41374038); The State Key Laboratory of Geodesy and Earth’s Dynamics Foundation of China (No. SKLGED2017-3-3-E)

GUO Rui(1982—), male, PhD, senior engineer, majors in satellite navigation, precise orbit determination and time synchronization.

CHEN Jinping

郭睿，陈金平，朱陵凤,等.北斗卫星超短弧运动学定轨方法优化与试验分析[J].测绘学报，2017,46(4)：411-420.

10.11947/j.AGCS.2017.20160361. GUO Rui, CHEN Jinping, ZHU Lingfeng,et al.Kinematic Orbit Determination Method Optimization and Test Analysis for BDS Satellites with Short-arc Tracking Data[J]. Acta Geodaetica et Cartographica Sinica,2017,46(4):411-420. DOI:10.11947/j.AGCS.2017.20160361.

P228

A

1001-1595(2017)04-0411-10

国家自然科学基金(41204022; 41374038)；大地测量与地球动力学国家重点实验室开放研究基金(SKLGED2017-3-3-E)

2016-07-15

郭睿(1982—),男,博士,高级工程师,研究方向为卫星导航、精密定轨与时间同步。

E-mail： shimbarsalon@163.com

陈金平

E-mail： jinping_chen@sina.com

修回日期： 2017-02-11