k-ε双方程水库水温模型浮力模拟分析

林 玲，梁瑞峰，李克锋，李 嘉

（四川大学 水力学与山区河流开发保护国家重点实验室，四川 成都 610065）

k-ε双方程水库水温模型浮力模拟分析

林 玲，梁瑞峰，李克锋，李 嘉

（四川大学 水力学与山区河流开发保护国家重点实验室，四川 成都 610065）

在比较国内外常用水库水温紊流模型的基础上，针对采用k-ε双方程紊流模型的宽度平均立面二维水库水温模型，从理论分析和数值模拟两方面讨论了k-ε紊流模型在模拟温差异重流时紊动动能生成项和浮力项的作用机理。分析了紊动动能生成项和浮力项对紊动动能和耗散率各自的影响程度，对水温垂向梯度与紊动动能的相互制约关系进行了探讨，研究了紊动动能浮力项和生成项在水库垂向的分布规律。W2模型根据实测数据率定的涡黏系数或混合长度在通用性上存在一定不足，但在使用者经验丰富的条件下仍能得到足够精确的预测结果。k-ε模型紊动动能生成项和浮力项引起的耗散率改变对紊动动能的影响作为小量可予忽略；k-ε模型可通过紊动动能生成项和浮力项计算与垂向流速和温度分布相适应的涡黏系数，将温差浮力影响反映在垂向动量方程中；浮力项主要受垂向温度梯度控制，紊动动能与垂向温度梯度的相互制约关系是k-ε紊流模型模拟温差异重流的关键因素。

紊流模型；紊动动能；浮力项；温差异重流

水库水温分层对水库水质、水生动植物及下游水生环境都具有重大影响。水温分层环境下的水库一般表层温度与气温变化同步，而具有较稳定的库底水温、一定的表层与底层温差和温跃层，温跃层范围内的水温在垂直方向上存在剧烈变化。这种环境下的水体流动属于湍浮力流，表现在垂向上由于温度差产生浮力，出现分层流动等异于等密度流的特殊流动形式。伴随这种流动，水库垂向出现水温分层形成、发展和消失的过程。水库的流场分布与水库的温度分布具有强烈的相互作用，因此准确模拟水库温度场的关键在于精确模拟浮力流流场。

k-ε紊流双方程模型是在单方程模型的基础上，增加确定紊动特征长度的微分输运方程而得到的，因而这种模型仍然采用了各向同性的紊动黏性系数的概念。在双方程模型中，标准k-ε模型在工程实际中得到了最广泛的应用和验证，它考虑了紊动速度比尺和紊动长度比尺的输运，对于大多数水流问题，标准k-ε双方程模型或其改进模型一般能得到较好的结果［1-3］。

标准k-ε模型也有其不足，如模型中经验常数的通用性尚不十分令人满意，另外，对于有些各向异性明显的水流或流动区域，有必要精确地描述应力各分量的输运，各向同性涡黏性系数的概念和据此建立起来的标准k-ε模型的适用性受到怀疑。有学者尝试采用各向异性的紊动黏性系数，如Young［4］在其二维水库模型中对垂向上的动量和热量的紊动扩散采用了不同经验公式。

也有学者直接采用各向同性的k-ε模型计算各向异性紊流流动。Farrell等［5］将k-ε模型应用于水库密度流的模拟，试验性地计算了一个100 m长的水库的下潜流过程，结果认为k-ε模型能够模拟出水库密度流的下潜、垂向旋涡和温度分层的特征现象。余真真［6-7］采用k-ε模型计算了温度分层环境对潮成内波和悬浮颗粒垂向输运的影响。邓云等［8］、刘兰芬等［9］也对水库温差异重流进行了模拟并得到了实测资料的验证［8-9］。

综上可知，k-ε模型能够模拟某些各向异性的紊流流动，如温差异重流，并得到了实验资料的良好验证，但上述文献并未从模型机理方面深入分析此类模拟成功的理论基础，故有必要在对比常用紊流模型的基础上从模型细节入手找出k-ε模型浮力模拟的主要影响因素。

1 模型对比

虽然有一些紊流模型不采用紊动黏性和紊动扩散的概念而采用紊动动量和紊动热（质量）通量的微分输运方程，但鲍辛涅斯克于1877年提出的紊动黏性概念至今仍是模拟雷诺应力的重要基础。根据紊流模型采用的微分输运方程的个数，以下从零方程、单方程和双方程三类模型分别对紊动黏性进行讨论。

1.1 零方程模型零方程模型或者据实验数据建立经验公式，或者将紊动黏性系数与时均速度建立联系，其中最为著名的当为普朗特提出的混合长模型：

式中：∂u∂y为流速梯度，1/s。

式（1）最难确定的参数即为混合长lm，对紊动量扩散输运和对流输运的忽略也使其在模拟复杂流动时易出现谬误。

CE-QUAL-W2模型是美国陆军工程兵团于1986年开发的宽度平均立面二维水质模型。对于湖泊和水库的温差异重流模拟，该模型推荐采用W2公式：

式中：vt为垂向涡流系数；κ为卡门常数；lm为混合长度；u为纵向流速；τwy为因风而产生的横向剪应力；k为波数；τytributary为因支流入流而产生的横向剪应力； ρ为水体密度；C为常数；Δzmax为垂向网格间距的最大值；Ri为理查森数：

式（2）通过Ri考虑了垂向密度梯度带来的紊动黏性变化。与普朗特的模型相比，式（2）另一主要改变在于将混合长直接定为计算网格的垂向最大间距，这就使紊动黏性系数vt的确定依赖于网格划分，实际上成为一个由使用者经验确定的系数。尽管可以采用实测数据对vt或者lm进行率定，但率定难免将影响水温的其它因素，如地形概化，转由vt或者lm承担，其适用性也存在一定疑问。

此外，CE-QUAL-W2的垂向动量方程式（4）采用了静水压力假定，实际是假定了在水库中垂向对流输移与扩散处于一种处处平衡的状态：

式中：p为压力；g为重力加速度；α为河底与水平线夹角。

由于密度中考虑了温度因素，静水压力假定并不排除因温度导致的浮力流速。只考虑两个方向时，据连续方程可得垂向流速w：

因而该模型在一定程度上是可以模拟温差浮力流的。

但在真实的水库环境中，处处平衡的对流输移与扩散毕竟不存在，简化过程中忽略的对流项将使模型难以模拟有垂向加速度的流场，如表层水体在降温期或夜晚遇冷下沉、冬季的低温水入库下潜等。忽略的扩散项导致缺乏对应的对流项对其进行平衡，通过压力计算和式（5）、纵向动量方程最终影响到流速的准确计算。

在求解包含完整的垂向动量方程的SIMPLE算法中，需要通过迭代解决动量方程确定的流场与连续方程确定的流场之间的不匹配问题，是较为耗时的。而CE-QUAL-W2通过静水压力假定和连续方程直接求解垂向流速，不需要解决流场在两个方程中的差异，因而其计算速度是比SIMPLE算法有较大优势的，且在使用者经验丰富的条件下仍能得出足够精确的预测结果。

1.2 单方程模型单方程模型的速度比尺 k由微分方程确定，柯莫哥洛夫和普朗特分别独立得到由速度和长度比尺确定的紊动黏性系数公式：

式中：C′μ为经验常数；k为紊动动能；L为长度比尺。

紊动动能的精确输运方程为：

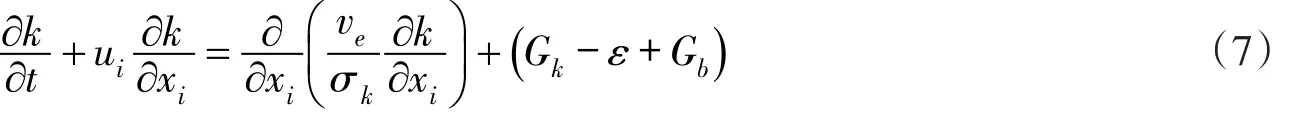
式中：ve为分子黏性系数v与紊动涡黏系数vt之和；σk为紊动普朗特数；Gk和Gb为紊动动能生成项和浮力项，β为等压膨胀系数；σT为紊动普朗特数。

封闭方程组的黏性耗散项通过因次分析得到：

式中：ε为紊动动能耗散率，CD亦为经验常数。

k方程考虑了浮力项Gb的影响，但长度比尺L如同混合长模型中的混合长度一样难以采用经验方法确定，限制了单方程模型的使用，其所能准确模拟的剪力层流动采用混合长模型也可得到满意的结果且计算更为简单。

1.3 双方程模型对表征漩涡尺寸的长度比尺紊动动能耗散率ε采用微分方程计算，单方程模型就转为双方程模型：

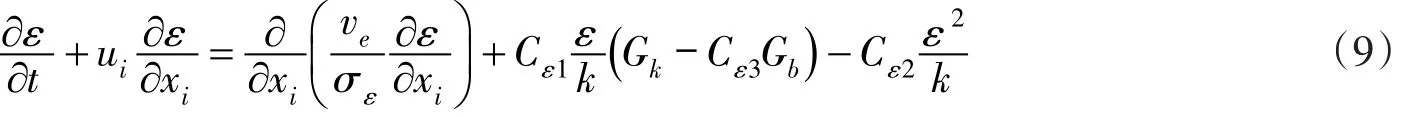
式中：σε为紊动动能耗散普朗特数；Cε1、Cε2、Cε3为模型常数。

双方程模型解决了单方程模型长度比尺的确定难题，同时，消去式（6）和式（8）中的长度比尺可得到：

式中：Cμ=C′μCD。Cμ避免了对和的各自单独确定，Cμ和Cε1、Cε2均可通过剪力层、近壁区等特殊区域的试验测定得到较为准确的数值。

但双方程在使用中如果采用完全的不可压缩假定，也将导致浮力模拟的偏差。如美国ANSYS公司的FLUENT软件，所采用的涡黏模型包括标准k-ε模型、RNGk-ε模型和Realizablek-ε模型，由于不可压流体假定使等压膨胀系数为零，垂向温差引起的密度流不能通过浮力项G来影响b涡黏系数，这些模型在计算温差异重流时是不能反映垂向密度差引起的热对流和紊动扩散的。

2 采用k-ε双方程紊流模型的宽度平均立面二维水库水温模型

虽然紊流问题均是三维问题，但在目前的技术经济条件下对大体积水体进行三维模拟在时间和必要性上尚存在较大改进空间，本文拟采用宽度平均的k-ε紊流模型和立面二维水库水温控制方程对影响浮力生成的紊动动能浮力生成项进行分析，阐明其模拟温差异重流的关键所在。

出于模型概化的考虑，在密度变化不大的浮力流问题中，Boussinesq认为可以近似地只在重力项中考虑浮力的影响，而在控制方程的其它项中忽略浮力的作用。当质量力仅为重力时，Navier-Stokes方程中的体积力可表达为：

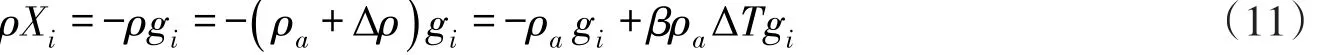
其中：ΔT=T-Ta，Ta为与参考密度 ρa相对应的参考温度；β为等压膨胀系数。将Boussinesq近似式（11）引入瞬时Navier-Stokes控制方程并通过k-ε双方程模化，在河宽方向作积分，可得到湍浮力流的宽度平均方程。式（12）—（16）分别为纵向动量、垂向动量、紊动动能和紊动动能耗散率以及温度方程：

由于水温在4℃时密度最大，在4℃左右的浮力作用规律是不一致的，本文只讨论水温大于4℃的情形，通过对k-ε紊流模型浮力项影响的分析确定其对温差异重流浮力模拟的具体影响因素。

3 原型水库

在对模型理论分析基础上，需要对水库进行模拟以直观说明各因素的实际作用和影响量级。

选取岷江上游的紫坪铺水库作为模拟水库。水库总库容为11.12×108m3，调节库容7.74×108m3，具有不完全年调节能力，正常蓄水位877 m，死水位817 m。现场观测表明该水库水温在升温期某些月份存在垂向分层现象，可用于验证模型的浮力计算效果。

收集到2009年11月6日、2010年7月6日紫坪铺水库全库区的水温观测以及同步的入库水温、气象、调度等资料，模型计算以2009年11月6日测量的全库区水温分布作为计算初始水温；流场计算据库尾入流水温进行多年循环计算，待库区水温稳定收敛后以11月6日的流场分布作为初始流场。图1为据实测库区水温作为初始条件计算得到的2010年5月15日的库区水温，温跃层在高程790 m左右。计算结果得到了紫坪铺水库实测数据的验证，成果将另文述评。

4 浮力模拟影响因素分析

热量在水体垂向上的传递主要依赖于随流输移和紊动扩散。在采用k-ε双方程的水库水温模型中，紊动动能k和耗散率通过涡黏系数影响热扩散系数和垂向流速w。

图1 紫坪铺水库2010年5月15日的库区水温分布（计算值）

4.1Gb和对Gk的影响紊动动能浮力项Gb使模型考虑了温度垂向分布对热扩散和紊动扩散的作用。为考察Gb对紊动动能k的影响，可据式（14）写出紊动动能的简化离散方程：

其中Lk表示本地输移和扩散对k的影响。

水温分层是通过浮力生成项Gb对紊动动能产生作用的。从式（17）可知，当T＞4℃，温度在垂向上存在正梯度，即稳定分层时，Gb为负值，直接抑制下一时刻紊动动能k的增长。

图2显示了水库垂向的紊动动能变化与温度梯度变化对比关系。水库表层温度梯度主要受太阳辐射和长波辐射等热通量控制，与同高程处的紊动动能无明显的相关关系。在发电引水孔口之上（高程820 m左右）的主流区域边缘，流速的垂向梯度因处于主流区域边缘而变化剧烈（见图3），使紊动生成项Gk增加从而带来较强的紊动，紊动扩散使区域内趋于同温，对应该高程处较低的温度梯度。而在靠近库底的780 m高程附近，各向流速和流速梯度均较小，缺乏紊动动能生成来源，垂向热量难以通过随流输移和紊动扩散传递，形成了局部较高的温度梯度。

图2 紫坪铺水库2010年5月15日坝前200 m的∂T∂z和k值

4.2 Gb、Gk对ε的影响紊动动能耗散率的简化离散方程为：

其中Lε表示本地输移和扩散对ε的影响。

紊动动能耗散也直接影响下一时刻的紊动动能（式（17），右侧-ε项），而温度垂向正梯度对kt、εt的作用是相反的。但由于Cε1和Cε2均小于1，通过和Cε3对Gb、Gk的“稀释”（式（18）），Gb、 Gk对ε的影响极为有限。图4给出了岷江紫坪铺水库2010年5月15日坝前200 m处的垂向值，可见温度分布对εt的作用与对kt的作用相比为小量，可以忽略。

图3 紫坪铺水库2010年5月15日坝前区域的流场

图4 紫坪铺水库2010年5月15日坝前200m的值

4.3 k、ε对涡黏系数vt的影响k、ε对随流输移和紊动扩散的影响通过涡黏系数vt来传递。

k-ε双方程计算得到的vt是各向同性的，但时均流通常具有倾向性的主流向，这种倾向性对大比尺紊动施加影响，使大比尺紊动具有很强的各向异性，紊动强度和紊动长度比尺因方向而异。如果雷诺数足够大，大比尺运动和小比尺运动在谱域上的间距足够大，方向灵敏性便完全消失，使得耗散能量的小比尺紊动变为各向同性［10］。在水库环境下，雷诺数变化范围较大，在流速较缓区域的流动具有各向异性特性，浮力对垂向对流的影响不可忽略，因而需要计算由浮力引起的vt变化。

由于一般情形下纵向流速总是远大于垂向流速，纵向动量方程中的惯性项主要由纵向压力梯度项来平衡，但垂向压力梯度与纵向压力梯度不在一个量级，因此垂向惯性项便主要由紊动扩散项和重力项平衡。此时垂向随流输移中的紊动输运项和热量方程中的热扩散项就对惯性项起着重要的平衡作用。另一方面，温度控制方程中不含有压力梯度项和浮力项，除非在源项很大的情形下，紊动输运项总是与惯性相平衡的重要因素，而除了表面热源外，水面下除了少量短波辐射进入外，一般不存在外来热源，因此在重力作用下，主流区域上边缘（图2，820 m附近）由于存在一定的垂向流速，对应地应存在较大的紊动扩散系数与惯性项平衡。

图5为紫坪铺坝前分别采用W2模型和k-ε模型计算的涡黏系数和水温。k-ε模型得到的涡黏系数分布与图2的流场是相匹配的，主流区域上边缘的大扩散系数也带来820 m高程上下的均温分布。但W2模型得到的涡黏系数由于主要受流速梯度和混合长度影响呈不规则分布且其量级远大于k-ε模型计算值，说明涡黏系数承担了本应由对流和垂向紊动扩散承担的输运部分。计算中，纵向流速u的上边界采用零梯度边界，这对W2模型和k-ε模型的影响是一致的，都导致了较小的涡黏系数，但W2模型由于缺乏垂向流速对强紊动的平衡，使表层热量难以进行对流输移，因而其表层水温高于k-ε模型计算值。

图5 紫坪铺水库2010年5月15日坝前200 m的涡黏系数和水温

5 结论

本文对国内外常用水库水温模型采用的紊流模型进行了对比，对其浮力模拟能力进行了分析，并以采用k-ε双方程紊流模型的宽度平均立面二维水库水温模型为基础，从理论分析和数值模拟两方面讨论了的k-ε紊流模型在模拟温差异重流时紊动动能浮力项和生成项的作用机理。研究表明：

（1）零方程的W2模型具有浮力模拟的理论基础，其涡黏系数的计算依赖于经验确定的混合长度，据实测数据率定的涡黏系数或混合长度将带入不确定的其它影响，使参数缺乏通用性，但在使用者经验丰富的条件下仍能得到足够精确的预测结果。

（2）双方程k-ε模型的紊动动能浮力项和生成项对紊动动能和耗散率的影响程度具有较大差异，紊动动能浮力项和生成项引起的耗散率改变对紊动动能的影响作为小量可予忽略。

（3）双方程k-ε模型可以通过紊动动能生成项和浮力项计算与垂向流速和温度分布相适应的涡黏系数，将温差浮力影响反映在垂向动量方程中；浮力项Gb主要受垂向温度梯度控制，紊动动能与垂向温度梯度的相互制约关系是k-ε紊流模型模拟温差异重流的关键因素。

［1］ 罗麟，赵文谦，李嘉.三维湍浮力回流数学模型在环境水力学中的应用［J］.水利学报，1992（9）：1-7.

［2］ 胡振红，沈永明，郑永红，等.温度和盐度分层流的数值模拟［J］.水科学进展，2001，12（4）：439-444.

［3］ BOURNET P E，DARTUS D，TASSIN B，et al.Numerical investigation of plunging density current［J］.J.Hy⁃dr.Engng.，1999，125（6）：584-594.

［4］ YOUNG D L.CHAPTER 10：Finite element analysis of stratified lake hydrodynamics［R］//Environmental Fluid mechanics—theories and applications.Edited by Hayley Shen，et al.2002.

［5］ GERARD J FARRELL，HEINZ G STEFAN.Mathematical modeling of plunging reservoir［J］.J.Hydraulic Re⁃search，1988，26（5）：525-537.

［6］ 余真真，王玲玲，朱海，等.三峡水库香溪河库湾潮成内波数值模拟［J］.四川大学学报：工程科学版，2012，44（3）：26-30.

［7］ 余真真，王玲玲，戴气超，等.水温分层对水体中悬浮颗粒物垂向输运影响的研究［J］.四川大学学报：工程科学版，2011，43（1）：65-70.

［8］ 邓云，李嘉，罗麟，等.河道型深水库的温度分层模拟［J］.水动力学研究与进展，2004，19（5）：604-609.

［9］ 刘兰芬，张士杰，刘畅，等.漫湾水电站水库水温分布观测与数学模型计算研究［J］.中国水利水电科学研究院学报，2007，5（2）：87-94.

［10］ 金忠青.N-S方程的数值解和紊流模型［M］.南京：河海大学出版社，1989.

The buoyance simulation analysis of k-ε double equation reservoir water temperature model

LIN Ling，LIANG Ruifeng，LI Kefeng，LI Jia
（State Key Laboratory of Hydraulics and Mountain River Engineering，Chengdu 610065，China）

Based on a comparative study of the reservoir water temperature turbulence models commonly used，a reservoir water temperature model with averaged width and 2-D elevation adopting k-ε double equa⁃tion turbulence model is used to simulate thermal density flow.In the view of theoretical analysis and nu⁃merical simulation，this paper discussed the mechanism of turbulent kinetic energy’s buoyancy term and pro⁃duction term.It investigated the buoyancy term’s and production term’s impacts on turbulent kinetic energy and energy dissipation，respectively.This paper explored the inter restricted relationship between water tem⁃perature vertical gradient and turbulent kinetic energy，and studied the vertical distribution law of turbulent kinetic energy’s buoyancy term and production term in reservoir.The eddy viscosity coefficient or mixing length in W2 model was lack of generality，which was rated by measured data，but a sufficient precise pre⁃diction result can be obtained by a veteran.The effect of the energy dissipation caused by the buoyancy term and production term on turbulent kinetic energy can be ignored as a small factor in k-ε turbulence model.This model can calculate eddy viscosity corresponding to the vertical velocity and temperature distri⁃bution by turbulent kinetic energy’s buoyancy term and production term.Therefore，the influence of thermal buoyancy was reflected in vertical momentum equation.The buoyancy term was mainly controlled by temper⁃ature vertical gradient.The inter restricted relationship of water temperature vertical gradient and turbulent kinetic energy was the key factor in a simulation of thermal density flow with the k-ε turbulence model.

turbulent model；turbulent kinetic energy；buoyancy term；thermal density flow

TV131.3

A

10.13244/j.cnki.jiwhr.2017.01.005

1672-3031（2017）01-0037-07

（责任编辑：李福田）

2016-04-08

国家自然科学基金项目（51279114）

林玲（1992-），女，四川泸州人，硕士生，主要从事环境水力学研究。E-mail：enidlinling@outlook.com

梁瑞峰（1974-），男，河南南阳人，博士，副研究员，主要从事环境水力学研究。E-mail：liangruifeng@scu.edu.cn