The Invariant Rings of the Generalized Transvection Groups in the Modular Case

HAN XIANG,NAN JI-zHUAND NAM KI-BONG

(1.School of Mathematical Sciences,Dalian University of Technology,Liaoning,116024)

(2.Department of Mathematics and Computer Science,University of Wisconsin-Whitewater, Whitewater,WI 53190,United States)

The Invariant Rings of the Generalized Transvection Groups in the Modular Case

HAN XIANG1,NAN JI-zHU1AND NAM KI-BONG2

(1.School of Mathematical Sciences,Dalian University of Technology,Liaoning,116024)

(2.Department of Mathematics and Computer Science,University of Wisconsin-Whitewater, Whitewater,WI 53190,United States)

Communicated by Du Xian-kun

In this paper,f i rst we investigate the invariant rings of the f i nite groupsG≤GL(n,Fq)generated byi-transvections andi-ref l ections with given invariant subspacesHover a f i nite f i eldFqin the modular case.Then we are concerned with general groupsGi(ω)andGi(ω)tnamed generalized transvection groups whereωis ak-th root of unity.By constructing quotient group and tensor,we calculate their invariant rings.In the end,we determine the properties of Cohen-Macaulay, Gorenstein,complete intersection,polynomial and Poincare series of these rings.

invariant,i-transvection,i-ref l ection,generalized transvection group

1 Introduction

LetFqbe a f i nite f i eld,whereq=pν,ν∈Z+.Suppose thatx1,···,xn∈V=form a basis andz1,···,zn∈V∗form the dual basis to{x1,···,xn}.We denote byFq[V]the graded ring of polynomial functions onV,which is def i ned to be the symmetric algebra onV∗.HenceFq[V]=Fq[z1,···,zn].IfGis a f i nite group,andρ:G→GL(n,Fq)is a representation ofGoverFq,then,viaρ,Gacts on the left of the vector spaceV=.The invariant ring(see[1],Page 4),denoted byFq[V]G,is

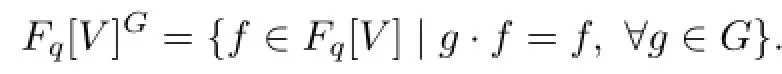
This is a graded subring ofFq[V].

In this paper,we are mainly concerned with the invariant rings of the groupsGgeneratedby elements with the codimensioniand some related properties over a f i nite f i eldFqin the modular case.In this case,the order ofGis divided by the characteristic of the f i eldFq.

A modern algorithm for the construction of invariant ring of groupGgenerated by elements with the codimension 1 can be found in[1].This problem is originally considered by Landweber and Stong[2]in connecting with their study of the depth of invariant ring. Years earlier Nakajima[3]studies the dual representations.And there is another way to obtain these results(see[4]).Much of the argument is devoted to showing that the invariant rings are polynomial.

For the groupde fi ned in De fi nition 1.3,Neuselet al.[5]–[6]construct the invariant ring.In[5],Neusel and Smith adopt a method associated to conf i gurations of hyperplanes.In[6],Nakajima determines f i nite irreducible subgroupsGof GL(V)such thatFq[V]Gare polynomial in the modular case.

A plan of the paper follows.In the remainder of this section,we illustrate the terminology used in this paper.In Section 2,we demonstrate the invariant rings of the groupsandGigenerated byi-transvections andi-ref l ections,respectively.Constructing quotient group and tensor is the key ingredient in the approach applied in this part.In Section 3,involving ak-th root of unityωwe def i ne a general groupGi(ω)named generalized transvection group.Then we investigate the invariant ring ofGi(ω)and its properties of Cohen-Macaulay, Gorenstein,complete intersection,polynomial and Poincare series.In the last section,we consider another generalized transvection groupGi(ω)twhich is the transpose of the groupGi(ω)and its properties.

We begin with a short review of some basic def i nitions concerning invariant and pseudoref l ection as a preliminary to introducei-transvection andi-ref l ection we need in this paper. We adopt the def i nitions from[5]and[7].

Def i nition 1.1[7]Given an element T∈GL(n,Fq).Denote the dimension of the subspaceIm(I−T)⊂V=Res(T).So the dimension of the subspaceker(I−T)overFqis equal to(n−Res(T)).

In a f i nite groupG⊆GL(n,Fq),a pseudo-ref l ection(see[5])T∈Gsatisf i es dimFq(Im(I−T))=1,i.e.,Res(T)=1.A pseudo-ref l ectionT/=Iis called a transvection ifT|(I−T)V=I, and a ref l ection ifT|(I−T)V=−I.Similarly,we def i nei-transvection andi-ref l ection.

Remark 1.1(1)Given ani-transvectionTwith a invariant subspaceHand a line subspaceL,sinceT|(I−T)V=Iand(I−T)V=Im(I−T),it yields that Im(I−T)⊆ker(I−T), i.e.,L⊆H.

Lemma 1.1Let T∈GL(n,Fq)satisfyRes(T)=i.Then T2|(I−T)V=I.

Proof.The result directly follows from Def i nition 1.2.

Def i nition 1.3Denote the group generated by all i-transvections with the same invariantsubspace H byH is called the invariant subspace ofDenote the group generatedby all i-transvections and all i-ref l ections with the same invariant subspace H by Gi,H.H iscalled the invariant subspace of Gi,H.For convenience,and Gi,Hare denoted byand Gi,respectively,in the sequel.

2 The Invariant Rings of the Groupsand Gi

The purpose of this section is to determine the structures of the invariant ringsand.Recall thatx1,···,xn∈V=form a basis andz1,···,zn∈V∗form the dual basis to{x1,···,xn}.LetH=ker〈zn−i+1,···,zn〉={v∈V|zj·v=0,forj=n−i+1,···,n}⊂Vbe the invariant subspace ofandGi.We emphasize that the invariants are relevant to the invariant subspaceH.IfHis not limited,the invariant is somewhat subtle and we will study in the future.

In order to determine the structures of the invariant ringsandFq[V]Gi,we need the matrix forms of elements in the groupsandGi.Denote by Matn−i,i(Fq)vector space of(n−i)×imatrices overFq.

Lemma 2.1The elements in the groupare of the forms

Proof.Sincez1,···,zn∈V∗form the dual basis andH=ker〈zn−i+1,···,zn〉is a subspace ofV,the proof is straightforward.

Lemma 2.2Let T∈GL(n,Fq)be an i-ref l ection with the invariant subspace H.Then T is of the form

Proof.The result directly follows from the def i nition of Res(T)=iand Lemma 1.1.

Now we consider the generators of the groupGi.

Proof.LetT1,T2∈Gibe twoi-ref l ections with the same invariant subspaceH.ThenT1T2is aj-transvection for some 1≤j≤i.Specially,j=iholds.Soi-ref l ections can generatei-transvections,which means that the groupGiis generated by alli-ref l ections. Hence the result follows.

The def i nitions of the groupsandGiare invalid forsince the def i nition of Res(T)=iis invalid forNevertheless,we f i nd that ifH=ker〈zt1,···,ztl〉is the invariant subspace of ani-transvection ori-ref l ection,theni=l.Hence we can extend the def i nition of Res(T)as follows.

Def i nition 2.1Let an element T∈GL(n,Fq)be of the form

where Mn−i,i∈Matn−i,i(Fq)is full column rank.Thenker(I−T)=ker〈zn−i+1,···,zn〉.

We denote the number i byRes(T).

According to Def i nition 2.1,Lemmas 2.1 and 2.3 both hold for alli=1,···,n−1. Furthermore,the invariant rings are well def i ned for alli=1,···,n−1 since they only depend on the matrix forms of generators in the groupsandGi.In the remainder of this section,we investigate the invariant rings ofandGi.

Recall that an invariant ringFq[V]Gof Krull dimensionnover the f i eldFqis called polynomial(see[1],Page 25)if there existnalgebraically independent invariantsf1,···,fnsuch thatFq[V]G=Fq[f1,···,fn].A sequenceh1,···,hk∈Fq[V]GFqis called a regular sequence(see[1],Page 114)ifh1is not a zero divisor inFq[V]Gandhiis not a zero divisor in the quotient ringFq[V]G/(h1,···,hi−1)fori=2,···,k,where(h1,···,hi−1)is the ideal inFq[V]Ggenerated byh1,···,hi−1.Ifh1,···,hkform the longest regular sequence inFq[V]Gandk=n,thenFq[V]Gis called Cohen-Macaulay(see[1],Page 129).

The invariant ringinvolves the top Chern classes and the Dickson polynomials. For an introduce see[1]and[5].Here we show the result.

Lemma 2.4([5],Proposition 3.3)Denote the top Chern class of zjby

where di,ris the Dickson polynomial in zn−i+1,···,znwith degree qi−qrfor r=0,···,i−1. Then

is polynomial.

Althoughis polynomial,is merely Cohen-Macaulay which will be proved in Proposition 3.2.Sinceis a normal subgroup ofGiand the quotient groupis isomorphic to the group,we can calculateFq[V]Gi.

Theorem 2.1With the preceding notations,ifcharFq=p=2,then

2,set N={n−i+1,···,n}andwhere Cqi(zj)is the top Chern class of zjgiven in Lemma2.4.Then

where{l1,···,lk}runs through all subsets of N.In particular,if i=1,then Fq[V]Gi=L.

Proof.If charFq=p=2,theni-transvections andi-ref l ections are precisely the same so we have.

If2,sinceandis given in Lemma 2.4,we need to compute.NoticeOn the one hand,the matrix−Ii∈GL(i,Fq)acting onFq[zn−i+1,···,zn]f i xes every Dickson polynomialdi,rin the formula ofCqi(zj).On the other hand,the matrix−Iif i xes all homogeneous polynomials inzn−i+1,···,znwith even degrees.Hence

where{l1,···,lk}runs through all subsets ofN={n−i+1,···,n}.Therefore,we have

where{l1,···,lk}runs through all subsets ofN={n−i+1,···,n}andL=,].

3 The Invariant Ring of the Generalized Transvection GroupGi(ω)

In this section,we consider a general caseGi(ω)named generalized transvection group.We fi rst state the de fi nition ofGi(ω)then deduce the invariant ringFq[V]Gi(ω)and its several properties.

In Lemma 2.3,the right bottom block of matrix form of generator inGiis(−1)×Ii. Now we consider a general case in which we substitute ak-th root of unityωfor−1.

Def i nition 3.1Let ω∈Fqbe a k-th root of unity.Def i ne a group

which is called the generalized transvection group.

In Section 4,we give another generalized transvection groupGi(ω)tin Def i nition 4.1. It is easy to see that the order|Gi(ω)|of the groupGi(ω)is equal tokq(n−i)i.Specially,Gi(ω)=ifk=1,andGi(ω)=Giifk=2.

Applying a similar method used in Theorem 2.1,we can get the invariant ringFq[V]Gi(ω).

Theorem 3.1Let ω∈Fqbe a k-th root of unity andbe the top Chern class ofzjfor j=1,···,n−i.SetThen

Now we adopt a similar method used in Theorem 2.1 to computerFq[V]Gi(ω).Sinceis a normal subgroup ofGi(ω)and the quotient groupis isomorphic to the group〈I(n−i)⊕ωIi〉,we obtain

In addition,is given in Lemma 2.4.Hence we need to compute

Sinceω∈Fqis ak-th root of unity,are all invariants wherek|(l1+···+li). For somej∈{1,···,i},iflj≥k,then

So we suppose 0≤l1,···,li≤k−1 andl1+···+li≤i(k−1).Hence

Notice thatωIi∈GL(i,Fq)acting onFq[zn−i+1,···,zn]f i xes every Dickson polynomialdi,r.Therefore,

whereM=Fq[Cqi(z1)].The proof is completed.

Since we have already got the invariant ring,what increases the interest in, and the importance of,is the properties of Cohen-Macaulay,Gorenstein,complete intersection and polynomial ofFq[V]Gi(ω).We investigate these properties in the sequel.

First of all,we prove thatFq[V]Gi(ω)is Cohen-Macaulay.We need a preliminary before stating a lemma used in the proof of the Cohen-Macaulay property.

Def i nition 3.2([8],Def i nition 2.4.6)If f1,···,fn∈Fq[V]Gis a homogeneous system of parameters,then fiis called primary invariant for i=1,···,n.Therefore,the invariant ring Fq[V]Gis a f i nite Fq[f1,···,fn]-module,say Fq[V]G=Kg1+Kg2+···+Kgm,where K=Fq[f1,···,fn]and g1,···,gm∈Fq[V]Ghomogeneous.The invariants g1,···,gmare called secondary invariants.

The following lemma allows us to determine whether an invariant ring is Cohen-Macaulay if we have known the primary and secondary invariants.

Lemma 3.1([8],Theorem 3.7.1)Assume that the action of G on V is faithful,let f1,···, fn∈Fq[V]Gbe primary invariants of degrees d1,···,dn,and{g1,···,gm}be a minimal system of secondary invariants.Then m|G|≥d1···dnwith equality if and only if Fq[V]Gis Cohen-Macaulay.

Notice that ifk=1 ori=1,the invariant ringFq[V]Gi(ω)is polynomial,so there only exists one secondary invariant 1.These cases are trivial and thus omitted.

is a minimal system of secondary invariants.

Proof.It is a direct conclusion by Theorem 3.1.

Proof.By Theorem 3.1,we have dimM(Fq·M)=1.SoN0=1.

Combining with the casej=1,the result follows.

Now we consider the Cohen-Macaulay property.

Proposition 3.2With the preceding notations,is Cohen-Macaulay.

Proof.Ifk=1 ori=1,thenis polynomial,so it is Cohen-Macaulay.

Ifk＞1 and 2≤i≤n−1,thenare all primary invariants by Lemma 3.2.The degrees ofandareqiandk,respectively.To f i nish the proof,we need to count the cardinal of the minimal system of secondary invariants in Lemma 3.2,i.e.,the value ofHowever,it is hard to compute the value by a straightforward method,so we come to another way.There existkiinvariantswith 0≤lλ＜kfor allλ∈{1,···,i}.Ifis a secondary invariant,then its degree is divided byk,so we have(modk).In addition,the order of the set

is equal toki−1according to number theory.This implies that there existki−1secondary invariants.With the preceding augmentation,it induces

The result follows from Lemma 3.1.

Remark 3.1Hochster and Eagon[9]proved that if a f i nite groupGacts on a Cohen-Macaulay ringRin the non-modular case,i.e.,the order of the groupGis not divided by the characteristic of the f i eld,thenRGis Cohen-Macaulay.In this paper,Proposition 3.2 demonstrates that in the modular case,i.e.,the order of the groupGi(ω)is divided by the characteristic ofFq,the invariant ringFq[V]Gi(ω)is also Cohen-Macaulay.

Next we consider the Gorenstein property.A commutative graded connected Noetherian algebra over a f i eld is called Gorenstein if it is Cohen-Macaulay and every parameter ideal is irreducible(see[1],Page 143).We prove that it only depends on the integersiandk.To begin with this we need the following characterization of the Gorenstein rings.

Lemma 3.3([1],Corollary 5.7.4)Let A be a Noetherian commutative graded connected Cohen-Macaulay ring of Krull dimension n and I⊂A a parameter ideal.Then the following conditions are equivalent:

(i)A is Gorenstein;

(ii)A/I is a Poincare duality algebra.

A commutative graded connected algebraAover a f i eldFqis called a Poincare dualit algebra of dimensionnif(i)Ai=0 fori＞n;(ii)dimFq(An)=1;(iii)the pairingAi⊗FqAn−i−→Angiven by multiplication is nonsingular for 0≤i≤n(see[1],Page 124).A nonzero element[A]ofAnis referred to as a fundamental class forA.

IfA=F[f1,···,fn]is polynomial,then it is Gorenstein since takingI=〈f1,···,fn〉as a parameter ideal we deduce thatA/Iis a f i eld,so a Poincare duality algebra.

Proposition 3.3With the preceding notations,it yields the following conclusions:

(1)If i=1,then Fq[V]Gi(ω)is Gorenstein;

(2)If1＜i and k≤i≤n−1,then Fq[V]Gi(ω)is Gorenstein⇐⇒k|i⇐⇒Gi(ω)⊂SL(n,Fq);

(3)If1＜i＜k,then Fq[V]Gi(ω)is not Gorenstein.

Proof.(1)Ifi=1,thenFq[V]Gi(ω)=]is polynomial by Theorem 3.1.SoFq[V]Gi(ω)is Gorenstein.

(2)If 1＜i≤n−1 andk=1,thenis polynomial so Gorenstein.

If 1＜i≤n−1 and 1＜k,to work with the Gorenstein property of,we need to obtain the information about the Poincare duality algebra.Hence we take

Ifis Gorenstein,thenHencel1=···=lifor a given secondary invariantwhereand 0≤l1,···,li≤k−1.Furthermore,sinceis the only one highest graded secondary invariant,we havel1=···=li=k−1.Therefore

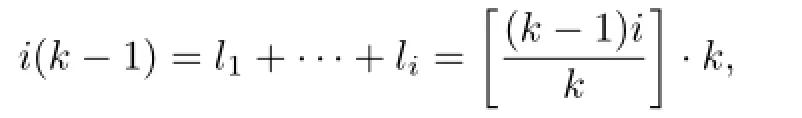
i.e.,

Conversely,ifk|i,then

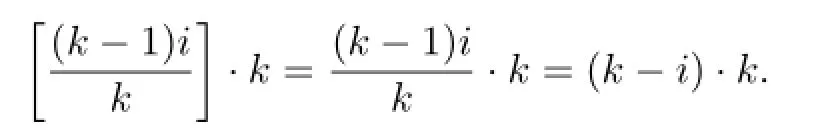
(3)If 1＜i＜k,suppose thatis Gorenstein,thenSincek＞i,we haveandl1,···,li＜k−1.Setl=l1=···=li＜k−1.Ifis a fundamental class,thenButwhich is algebraically independent withf1,is another fundamental class with the same degree since 0＜l＜k−1 and 1＜i.Hence,which is a contradiction.Therefore,is not Gorenstein.

Remark 3.2In[10]and[11],Stanleyet al.proved a similar result in the non-modular case.In[12],Braun proved that if a groupGcontains no pseudo-ref l ection,then there is a similar result.In this paper,sinceis a subgroup ofandcontains 1-transvections(i.e.,pseudo-ref l ections),the groupGi(ω)indeed contains pseudo-ref l ections. In addition,is Gorenstein ifk|i.Hence we improve the result of[12]in a way.

The following corollary is a byproduct according to the preceding discussion.

Corollary 3.1If1＜i≤n−1and1＜k,we have

where

Furthermore,if i=k·l,where l∈Z+,then

Proof.This is an immediate consequence of the proofs of Theorem 3.1,Propositions 3.1, 3.2 and 3.3.

Recall that a commutative ringAover the f i eldFqis called a complete intersection ifA～=Fq[f1,···,fm]/(h1,···,ht),whereh1,···,ht∈Fq[f1,···,fm]are algebraically independent andFq[f1,···,fm]is a freeFq[h1,···,ht]-module(see[1],Page 68).HenceAis Gorenstein ifAis a complete intersection.In[13],Kac and Watanabe proved that if an invariant ring of a groupGis a complete intersection,then the groupGis generated by biref l ections,i.e.,elementsg∈Gsuch that Res(g)≤2.

Proposition 3.4(1)If i=1,then Fq[V]Gi(ω)is a complete intersection.

(2)If i=2and k=1,2,then Fq[V]Gi(ω)is a complete intersection;if i=2and2＜k, then Fq[V]Gi(ω)is not a complete intersection.

(3)If2＜i≤n−1,then Fq[V]Gi(ω)is not a complete intersection.

Proof.(1)Ifi=1,thenFq[V]Gi(ω)=Mis polynomial.So it is a complete intersection.

(2)Ifi=2 andk=1,thenis polynomial so a complete intersection.

Ifi=k=2,then

is a complete intersection.

Ifi=2＜k,thenFq[V]Gi(ω)is not Gorenstein by Proposition 3.3.Hence it is not a complete intersection.

(3)If 2＜i≤n−1,it directly follows from Theorem A of[13].

Proposition 3.5Suppose2≤i≤n−1.Let K be a subgroup of Gi(ω).If Fq[V]Kispolynomial,then K contains no i-ref l ection,i.e.,K is a subgroup of.

Proof.In[14],Serre stated that a groupGis a pseudo-ref l ection group ifFq[V]Gis polynomial.SoKis generated by 1-ref l ections and 1-transvections sinceFq[V]Kis polynomial. Moreover,there is no 1-ref l ection in the groupGi(ω)for 2≤i≤n−1.HenceKis only generated by 1-transvections,i.e.,Kis a subgroup of.

Then we focus on the secondary coeffi cient of the Laurent expansion.

Proposition 3.6The Poincare series of Fq[V]Gi(ω)is

(1)if i=1,then

(2)if2≤i≤n−1,then

According to series theory,we have

Ifi=1,then

If 2≤i≤n−1,then

Therefore,ifi=1,then

And if 2≤i≤n−1,then

Remark 3.3A formula for the second coeffi cient has been obtained by Benson and Crawley-Boevey[15]for the prime f i eldFp.In addition,Hartmann[16]gave the ramif i cation formula and attendant inequality for arbitrary f i elds.The formulas they given are verycomplicated.Here we simplify the formula in a special case.Furthermore,we give an algebraic conjecture.

Def i nition 3.4Def i ne a set

It is a subset of Gi(ω)and its cardinal is equal to(qi−1)(n−i).

Conjecture 3.1Denote byC(τi(ω))the cardinal ofτi(ω).

(1)Ifi=1,then

(2)If 2≤i≤n−1,then

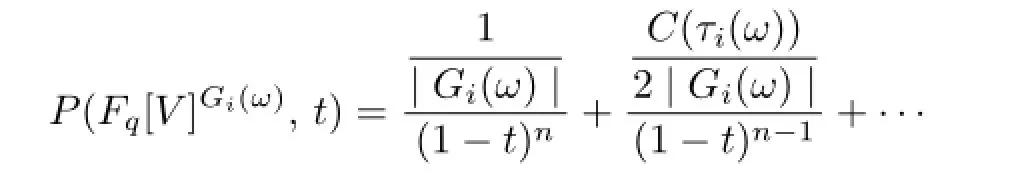
4 The Invariant Ring of the Group Gi(ω)t

In this section,we consider the invariant ring of another generalized transvection groupGi(ω)tand its properties.The groupGi(ω)tis def i ned as follows.

Def i nition 4.1Let ω∈Fqbe a k-th root of unity.Def i ne a group

It is easy to see that the order|Gi(ω)t|is equal tokq(n−i)i.In fact,the elements in the groupGi(ω)tare transpose of the elements inGi(ω).That is the reason we use the symbolGi(ω)t.

In the remainder of this section,we investigate the results of the groupGi(ω)t.SinceGi(ω)tis the transpose ofGi(ω)in a way,the results ofGi(ω)tare similar to the ones ofGi(ω).Hence we omit the proofs as they are proved by the similar methods.

We f i rst calculate the invariant ring of the groupGi(ω)t.

Theorem 4.1Let ω∈Fqbe a k-th root of unity and Cqn−i(zj)be the top Chern class of zjwith degree qn−ifor j=n−i+1,···,n.Set Mt=Fq[z1···,Cqn−i(zn)k].Then

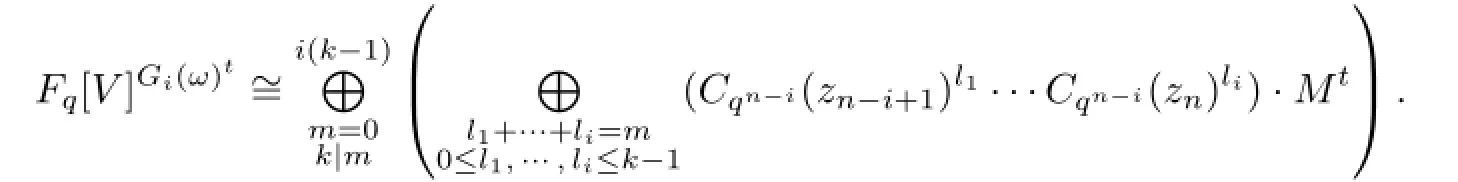
In particular,if k=1,i.e.,ω=1,then Fq[V]Gi(ω)t=Mtis polynomial.

The primary and secondary invariants are given in the following lemma which are used to prove the Cohen-Macaulay property.

Lemma 4.1Suppose1＜k and2≤i≤n−1.In the invariant ring Fq[V]Gi(ω)tgiven in Theorem4.1,z1,···,zn−i,Cqn−i(zn−i+1)k,···,Cqn−i(zn)kare all primary invariants and

is a minimal system of secondary invariants.

Ifk=1 ori=1,thenFq[V]Gi(ω)tis polynomial.Hence these cases are omitted.

Def i nition 4.2Suppose that1＜k and2≤i≤n−1.In the minimal system of secondary invariants of Fq[V]Gi(ω)tgiven in Lemma4.1,denote the number of the secondary invariantswith degree qn−ijk by,where j=0,···,

Proposition 4.2With the preceding notations,Fq[V]Gi(ω)tis Cohen-Macaulay.

Next we come to the properties of Gorenstein,complete intersection and polynomial.

Proposition 4.3(1)If i=1,then Fq[V]Gi(ω)tis Gorenstein.

(2)If1＜i≤n−1and k≤i,then Fq[V]Gi(ω)tis Gorenstein⇐⇒k|i⇐⇒Gi(ω)t⊂SL(n,Fq).

(3)If1＜i＜k,then Fq[V]Gi(ω)tis not Gorenstein.

Proposition 4.4(1)If i=1,then Fq[V]Gi(ω)tis a complete intersection;

(2)If i=2and k=1,2,then Fq[V]Gi(ω)tis a complete intersection;if i=2and2＜k, then Fq[V]Gi(ω)tis not a complete intersection;

(3)If2＜i≤n−1,then Fq[V]Gi(ω)tis not a complete intersection.

Proposition 4.5Suppose2≤i≤n−1.Let Ktbe a subgroup of Gi(ω)t.If Fq[V]Ktispolynomial,then Ktcontains no i-re fl ection,i.e.,Ktis a subgroup of,where=

In the end,we investigate the Poincare series ofFq[V]Gi(ω)t.SinceFq[V]Gi(ω)tis dif f erent fromFq[V]Gi(ω),the Poincare series is not yet same.

Proposition 4.6The Poincare series of Fq[V]Gi(ω)tis

4.2for j=0,···,

(1)If i=1,then

(2)If2≤i≤n−1,then

There is also a conjecture about the second coeffi cient of the Laurent expansion.

Def i nition 4.3Def i ne a set

It is a subset of Gi(ω)tand its cardinal is equal to i(qn−i−1).

Conjecture 4.1Denote byC(τi(ω)t)the cardinal ofτi(ω)t.

(1)Ifi=1,then

(2)If 2≤i≤n−1,then

[1]Neusel M D,Smith L.Invariant Theory of Finite Groups:Mathematical Surveys and Monographs.Amer.Math.Soc.,vol.94,2002.

[2]Landweber P S,Stong R E.The Depth of Rings of Invariants over Finite Fields.Berlin,New York:Springer-Verlag,1987.

[3]Nakajima H.Invariants of f i nite abelian groups generated by transvections.Tokyo J.Math., 1980,3:201–214.

[4]Orlik P,Terao H.Arrangements of Hyperplanes.Heidelberg,Berlin:Springer-Verlag,1992.

[5]Neusel M D,Smith L.Polynomial invariants of groups associated to conf i gurations of hyperplanes over f i nite f i elds.J.Pure Appl.Algebra,1997,122:87–105.

[6]Nakajima H.Invariant of f i nite groups generated by pseudo-ref l ections in positive characteristic.Tsukuba J.Math.,1979,3(1):109–122.

[7]You H,Lan J Z.Decomposition of matrices into 2-involutions.Linear Algebra Appl.,1993, 186:235–253.

[8]Derksen H,Kemper G.Computational Invariant Theory.Heidelberg,Berlin:Springer-Verlag, 2002.

[9]Hochster M,Eagon J A.Cohen-Macaulay rings,invariant theory,and the generic perfection of determinantal Loci.Amer.J.Math.,1971,93(4):1020–1058.

[10]Stanley R P.Invariants of f i nite groups and their applications to combinatorics.Bull.Amer. Math.Soc.,1979,1(3):475–512.

[11]Bruns W,Herzog J.Cohen-Macaulay Rings.Cambridge:Cambridge Stud.Adv.Math.,Cambridge University Press,1998.

[12]Braun A.On the gorenstein property for modular invariants.J.Algebra,2011,345:81–99.

[13]Kac V,Watanabe K I.Finite linear groups whose ring of invariants is a complete intersection.Bull.Amer.Math.Soc.,1982,6:221–223.

[14]Serre J P.Groups f i nis d’automorphismes d’anneaux locaux reguliers.Colloq.d’Alg.Ec.Norm. Sup.de Jeunes Filles,1967,8:1–11.

[15]Benson D J,Crawley-Boevey W W.A ramif i cation formula for poincare series,and a hyperplane formula for modular invariants.Bull.London Math.Soc.,1995,27:435–440.

[16]Hartmann J.Transvection free groups and invariants of polynomial tensor exterior algebra.Transform.Groups,2001,6:157–164.

tion:13A50,20F55,20F99

O152.6

1674-5647(2017)02-0160-17

10.13447/j.1674-5647.2017.02.08

Received date:Nov.1,2016.

Foundation item:The NSF(11371343)of China.

E-mail address:xianghan328@yahoo.com(Han X).