Uniqueness in Determining a Ball with a Single Incoming Wave

LIU JUAN AND ZHANG JIE

(Department of Mathematics,Jinan University,Guangzhou,510632)

Uniqueness in Determining a Ball with a Single Incoming Wave

LIU JUAN AND ZHANG JIE

(Department of Mathematics,Jinan University,Guangzhou,510632)

Communicated by Ma Fu-ming

We prove that a ball with the impedance boundary condition is uniquely determined by the far-f i eld pattern corresponding to an incident plane wave at one given wavenumber and one given incident direction.In the uniqueness proof,the impedance parameter in the impedance boundary condition is unknown.

inverse obstacle scattering,uniqueness,ball,impedance boundary condition,Helmholtz equation

1 Introduction

In this paper,we mainly consider the uniqueness of an inverse acoustic obstacle scattering problem.Mathematically,the scattering of time-harmonic acoustic waves by an obstacle embedded in a homogeneous medium can be formulated as the following acoustic obstacle scattering problem:LetG⊂R3be an impenetrable bounded obstacle with aC2-smooth boundary surface and an unbounded and open connected complement,given an incident fi eldui(x)=eikx·dwith wavenumberk＞0 and incident directiond, fi nd the scattered fi eldusand the total f i eldu=ui+ussuch that

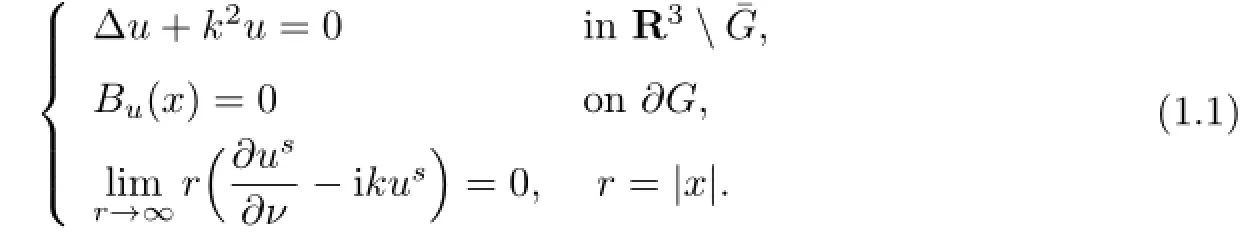
whereνis the exterior unit normal vector to∂G.The operatorBuin(1.1)def i nes the boundary condition,the frequently occurring boundary condition is the impedance boundarycondition

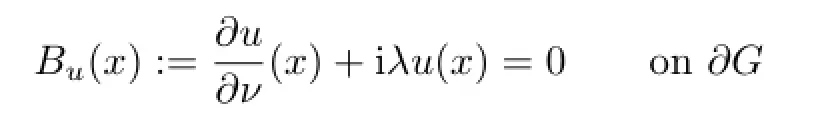
for impedance obstacle with some real-valued impedance parameterλ≥0 on∂G.The Dirichlet boundary condition for sound-soft obstacle is the impedance boundary condition withλ=∞,and the Neumann boundary condition for sound-hard obstacle is the impedance boundary condition withλ=0.

It is known that the scattered f i eldushas an asymptotic behavior of the form

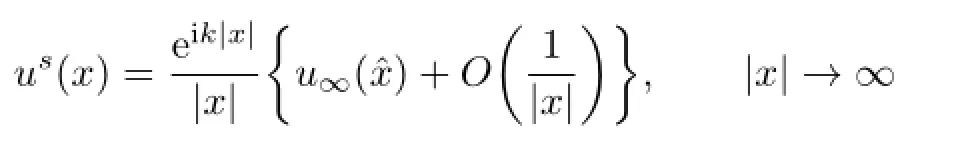
uniformly in all directionsˆx=x/|x|,where the functionu∞def i ned on the unit sphere S2is known as the far-f i eld pattern ofus.

The inverse acoustic obstacle scattering problem is to determine the shape and location of the scattererGfrom a knowledge of the far-f i eld patternu∞.This problem is important in many applications,such as radar/sonar applications,geophysical exploration and medical imaging.One of the fundamental issues for the inverse problem is the uniqueness,i.e., whether the scatterer can be uniquely determined by the given far f i eld pattern.

Most of the existing works on the uniqueness problem identify the obstacle with the far-f i eld patterns from inf i nitely or countably many incident plane waves(see[1],[2]and references therein).Nevertheless,there is a widespread belief that one can establish the uniqueness in determining an obstacleGby the far-f i eld pattern from a single incident plane wave(see[2]).Some reconstruction schemes with a single incident wave have been developed (see,e.g.,[3]–[5]),while the uniqueness still remains largely open in the literature,though signif i cant ef f orts have been devoted to such a study(see[6]–[12]).

Assuming the scatterer to be a ball may be a nice try to establish the uniqueness for one incident wave,because anyC2-smooth obstacle is isomorphic to a ball.With the farfi eld pattern from a single incident plane wave,Liu[9]established a uniqueness result for the sound-soft ball and Yun[10]established a uniqueness result for the sound-hard ball.[11]and [12]even showed that a sound-soft/sound-hard ball can be uniquely determined by some farfi eld data measured at some fi xed spots corresponding to a single incident plane wave.Could uniqueness be established for impedance ball?In the present paper,we make a step towards this direction.We prove that an impedance ball without the impedance parameter provided can be uniquely determined with only the far-f i eld pattern from just a single incident plane wave.As a matter of fact,the uniqueness result in the present work includes the uniqueness results in[9]and[10].To our knowledge,this is the f i rst result of such kind for the impedance ball.The proof is inspired by the proof of Theorem 5.4 in[1],it is based on a translation property of the far f i eld pattern,and also the series expansion of the scattered wave f i elds for an impedance ball.Finally,we wish to remark that we are only concerned with the three-dimensional case,but all the result obtained can be straightforwardly extended to the two-dimensional case.

2 Translation Property of the Far Field Pattern

LetD⊂R3be an impedance ball centered at the origin with radiusR,letDz:={x+z;x∈D}be a shifted ball ofDwith the shiftz∈R3.The far f i eld pattern forDandDzcorresponding to the incident plane wave eikx·disu∞andu∞,z(ˆx),∈S2.One question is meaningful to our uniqueness proof,that is,are there any connections betweenu∞andu∞,z?We give a def i nite answer to the question in this section.

In fact,ifDandDzare both sound-soft balls,u∞andu∞,zhave the translation property (cf.[1])

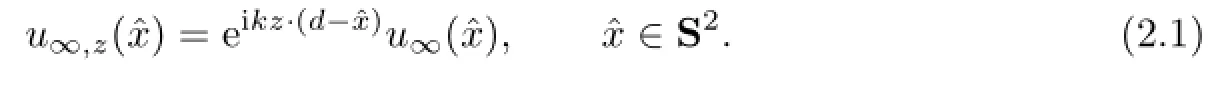
IfDandDzare both impedance balls,we are able to derive the same translation property of the far f i eld pattern in the following theorem.

Theorem 2.1Let D and Dzbe both impedance balls,and let the incident wave beeikx·d. For the far f i eld pattern u∞and u∞,zcorresponding to D and Dz,we have

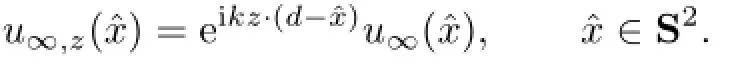
Proof.Letbe the scattered wave forDzcorresponding to incident wave eikx·d.With variable substitutiony=x−z,x∈R3,we def i ne

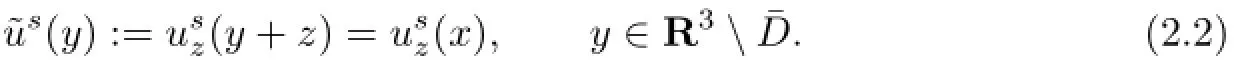
,is the scattered wave forDzcorresponding to the incident wave eikx·d,sois the scattered wave forDcorresponding to the incident wave eik(y+z)·d.

Letus(y)be the scattered wave for the impedance ballDcorresponding to eiky·d.Denote bythe f i rst-kind spherical Hankel function of ordern,and denote by,m=−n,···,nthe 2n+1 orthonormal spherical harmonics of ordern,thenus(y)has an expansion of the form(see[1])

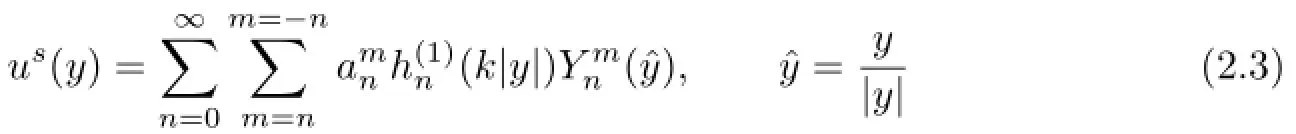
with coeffi cients

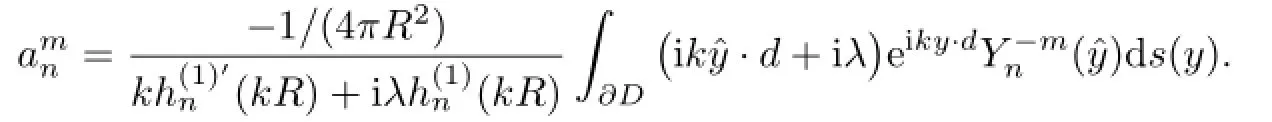
Similarly,the scattered wavefor the impedance ballDcorresponding to eik(y+z)·dhas an expansion of the form

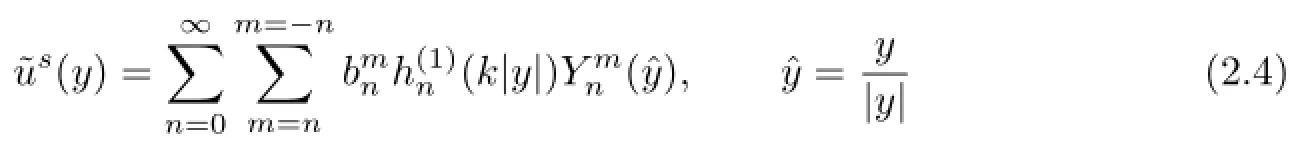
with coeffi cients

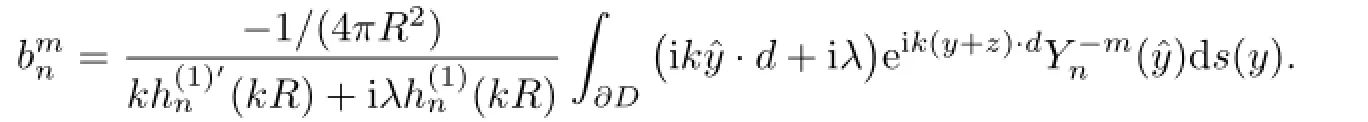
We see from(2.3)and(2.4)that

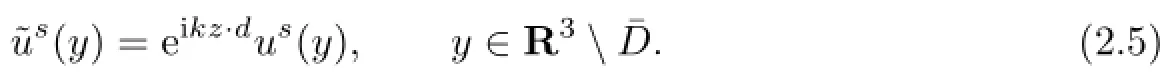
In view of(2.2)and(2.5),we have

we would like to emphasize that,andy=x−z,.

Next we consider the far f i eld pattern of(2.6).

us(y)has the asymptotic behavior

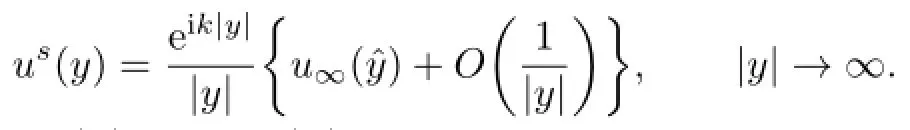
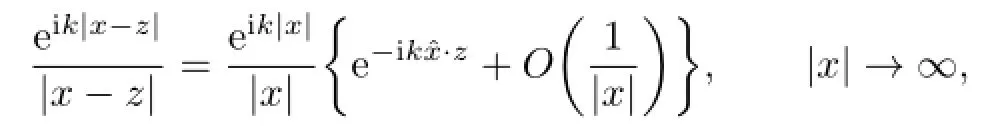
shows

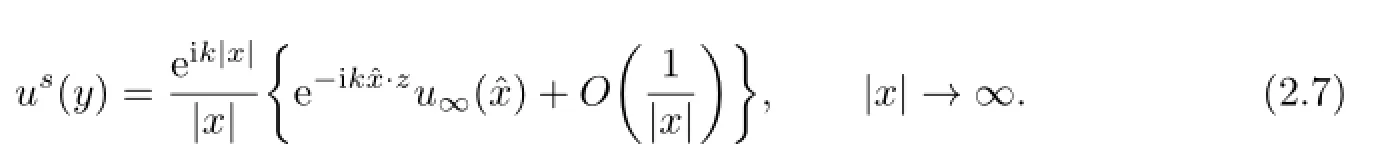
Combining(2.6)and(2.7),we have

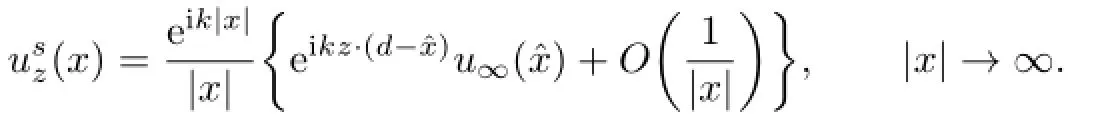
By the def i nition of the far f i eld pattern,we conclude that the corresponding far f i eld pattern ofis

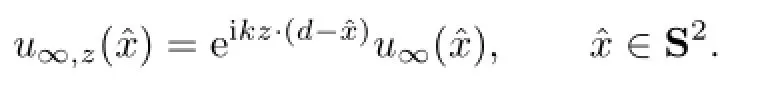
3 Uniqueness Result

For general smooth obstacles,one existing uniqueness result is shown in the following theorem(see[1]).

Theorem 3.1Assume that G1and G2are two scatterers with boundary conditions B1and B2such that the far f i eld patterns coincide for an inf i nite number of incident plane waves with distinct directions and one f i xed wavenumber.Then G1=G2and B1=B2.

We can see that the far f i eld patterns for inf i nite incident plane wave uniquely determines the scatterer without the boundary condition known.When the scatterer is a ball,which has more simple geometry structure,one may identify the object with less data.In this section,we present our uniqueness result on determining an impedance ball without the impedance parameter known.

For future reference,we present the scattered wave and its far f i eld pattern corresponding to an incident plane wave for an impedance ball,which is centered at the origin with radiusR.According to(2.3),the scattered waveus(x),for an impedance ballDis given by

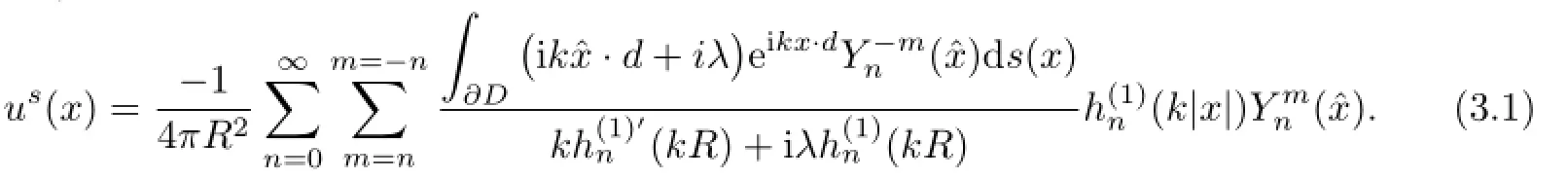
Letjn(t)andPn(t)be the f i rst-kind spherical Bessel function and the Legendre polynomial of ordern,letθdenote the angle betweenand the incident directiond.In view of theFunk-Hecke formula(see[1])

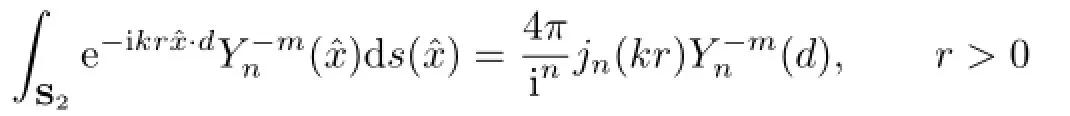
and the addition formula(see[1])

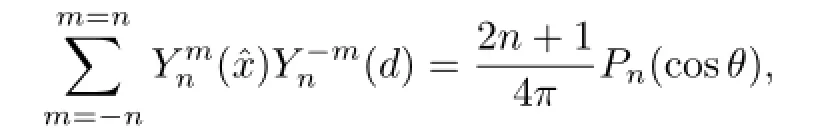
the scattered waveus(x),x∈R3¯Din(3.1)is easily derived to be

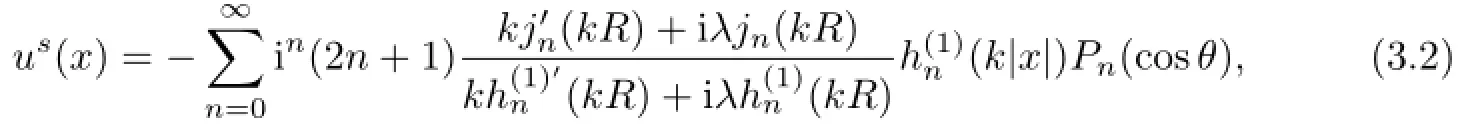
Its corresponding far-f i eld pattern is given by

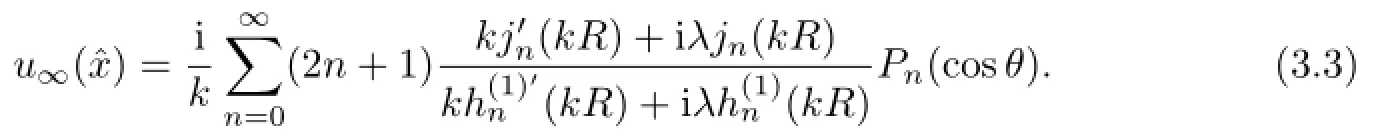
By the asymptotic behavior of the spherical Bessel and Hankel functions for largen,we have

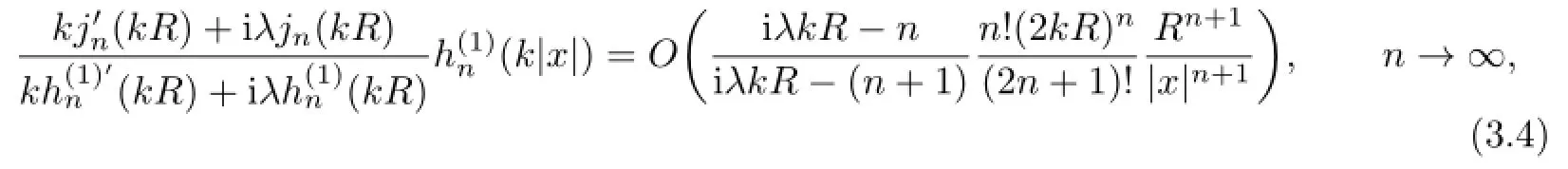
uniformly on compact subsets of R3{0}.Therefore,the series(3.2)is uniformly convergent on compact subsets of R3{0}based on ratio test.By Theorem 2.15 in[1]the series represents a radiating f i eld in R3{0},so the scattered waveus(x),which solves the scattering problem for the impedance ball,can be extended frominto R3{0}.

Now we are ready to present our uniqueness result in the following theorem.

Theorem 3.2If a ball is an impedance ball with constant impedance parameter,it can be uniquely determined by the far f i eld pattern for one incident plane wave without the impedance parameter known.

Proof.Assume that two ballsDz1andDz2with centersz1andz2have the same far fi eld patternu∞,z1=u∞,z2for scattering of one incident plane wave.Then by Rellich’s lemma(see Lemma 2.12 in[1]),the scattered waves coincide inand we can identifyin.Now assume thatz12.Then from the explicit solution(3.2)and Lemma 3.1,considering the relation(2.6),we have thathas an extension intoandhas an extension into R3z2.Therefore,uscan be extended frominto all of R3,that is,usis an entire solution to the Helmholtz equation.Consequently,sinceusalso satisf i es the radiation condition it must vanish identically in all of R3.Then the total f i eld coincides with the incident f i eld and this leads to a contradiction since the plane wave cannot satisfy the boundary condition.

Therefore,the two ballsDz1andDz2must have the same center.For a ball centered at the origin,from(3.3)we observe that the far f i eld pattern only depends on the angle between the incident and the observation direction,so the far f i eld patterns for all incident directions can be obtained from the far f i eld patterns for one incident plane wave.Therefore, in view of Theorem 2.1,coincidence of the far f i eld pattern for one incident plane wave fromthe two ballsDz1andDz2with the same center implies coincidence of the far f i eld patterns for all incident directions.Now the statement of the theorem follows from Theorem 3.1.

[1]Colton D,Kress R.Inverse Acoustic and Electromagnetic Scattering Theory.3rd ed.,New York:Springer,2012.

[2]Kress R.Uniqueness and numerical methods in inverse obstacle scattering.J.Phys.:Conf. Ser.,IOP Publishing,2007:012003–012018.

[3]Potthast R,Sylvester J,Kusiak S.A‘range test’for detemining scatterers with unknown physical properties.Inverse problem,2003:19(3):533–547.

[4]Serranho P.A hybrid method for inverse scattering for sound-soft obstacle in R3.Inverse Problems and Imaging,2007:1:691–712.

[5]Liu J,Dai L.An iterative decomposition method for scatterer reconstruction in R3.J.Comput. Appl.Math.,2015:287:148–161.

[6]Alessandrini G,Rondi L.Determining a sound-soft polyhedral scatterer by a single far-f i eld measurement.Proc.Amer.Math.Soc.,2005,133(6):1685–1691.

[7]Cheng J,Yamamoto M.Uniqueness in an inverse scattering problem within non-trapping polygonal obstacles with at most two incoming waves.Inverse Problems,2003,19(6):1361–1384.

[8]Liu H Y,Zou J.Uniqueness in an inverse acoustic obstacle scattering problem for both soundhard and sound-soft polyhedral scatterers.Inverse Problems,2006,22(2):515–524.

[9]Liu C.An inverse Obstacle Problem:A Uniqueness Theorem for Balls,Inverse Problems in Wave Propagation.Berlin-Germany:Springer,1997,pp.347–355.

[10]Yun K.The ref l ection of solutions of Helmholtz equation and an application.Commun.Korean Math.Soc.,2001,16(3):427–436.

[11]Liu H Y,Zou J.Zeros of the Bessel and spherical Bessel functions and their applications for uniqueness in inverse acoustic obstacle scattering.IMA J.Appl.Math.,2007,72:817–831.

[12]Hu G H,Liu X D,Zhang B.Unique determination of a perfectly conducting ball by a f i nite number of electric far f i eld data.J.Math.Anal.Appl.,2009,352(2):861–871.

[13]Cakoni F,Colton D.Qualitative Methods in Inverse Scattering Theory:An Introduction.New York:Springer Science&Business Media,2005.

tion:78A46,35J25

A

1674-5647(2017)02-0143-06

10.13447/j.1674-5647.2017.02.06

Received date:April 23,2016.

Foundation item:Guangdong Natural Science Foundation(2016A030313074)of China.

E-mail address:liujuan@jnu.edu.cn(Liu J).