P-congruence-free Epigroups
LIU JING-GUOAND ZHANG JIN-LING
(1.School of Mathematics and Statistics,Linyi University,Linyi,Shandong,276005)
(2.Lanshan Education and Physical Education Bureau,Linyi,Shandong,276005)
P-congruence-free Epigroups
LIU JING-GUO1AND ZHANG JIN-LING2
(1.School of Mathematics and Statistics,Linyi University,Linyi,Shandong,276005)
(2.Lanshan Education and Physical Education Bureau,Linyi,Shandong,276005)
Communicated by Du Xian-kun
LetPdenote the equivalence relation on an epigroup in which any of its classes consists precisely of those elements owning the same pseudo-inverse.The purpose of the paper is to characterize epigroups on which any congruence either containsPor its join withPis the identity relation on epigroups.As a special subclass of epigroups,completely 0-simple semigroups having the same property are also described.
congruence,epigroup,completely 0-simple semigroup
1 Introduction and Preliminaries
An epigroup is a semigroup in which some power of any element lies in a subgroup of the given semigroup.The works by Shevrin were devoted to di ff erent structural aspects of epigroup theory(see[1]–[3]).For an elementxof a given epigroup,letbe the identity of the subgroupGthat contains some power ofx,andthe group inverse ofxxω(=xωx) inG,which is called the pseudo-inverse ofx.An epigroup can alternatively be regarded as a unary semigroup with the unary operation of taking pseudo-inversedue to Shevrin(see also[1]and[2]).Further new result on epigroups as unary semigroups about this operation,for instance,occurred in[4].In[5],the equivalence relationPon an epigroup, in which its arbitrary classes consist precisely of those elements having the same pseudoinverse,was introduced,and several characterizations of epigroups in whichPis a congruence were also given.In[6],the relation on the congruence lattice of an epigroup that identi fi es two congruences if they have the same join withPwas considered.In fact,for a better understanding of congruences on some special semigroups,an essential role is played by theinterplay of an arbitrary congruence with some known equivalence relations,such as Green’s relationsH,L,R,DandJ,which leads to various decompositions of the congruence lattice of a semigroup,helping us to gain insight into the structure of the congruence lattice,even some information on the semigroups.One direction of this idea was ref l ected in[7],where the authors classed the completely regular semigroups on which any congruence either contains some Green’s relationG,or its join withGis the identity relation on the semigroups.
The lattice of congruences of a semigroupSis denoted byC(S),which is partially ordered by inclusion.Recall that for an equivalence relationτonS,Sis called to beτ-congruencefree if for anyρ∈C(S),eitherρ∩τ=∆orτ⊆ρ(see Def i nition 1.1 in[7]).
In this paper we characterizeP-congruence-free epigroups.In Section 2,we deal with P-congruence-free completely 0-simple semigroups and classify them.The main result formulated in Section 3 provides the classif i cation and description ofP-congruence-free epigroups.In Section 1,besides required background information concerning epigroups,we present basic information and auxiliary facts aboutP-congruence-free epigroups.Here we generally follow the notation and terminology of[8]and[9];in particular,we recall the following concepts.
An elementa′in a semigroupSis an inverse ofainSifaa′a=aanda′aa′=a′.The set of inverses ofais denoted byV(a),andais regular ifV(a)is not empty.The set of all completely regular elements of a semigroupS(i.e.,the group part ofS)is denoted by GrS.IfShas a zero,NilS={s∈S:sn=0 for somen∈Z+}.For an epigroupS,the equivalence relationPonSis def i ned by
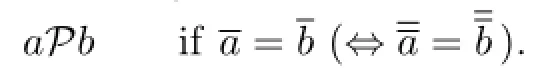
Notice that for any,then,so thatand noP-class contains more than one completely regular element.
The following Lemma is a corollary of Theorem 6.45 in[10].
Lemma 1.1Let S be an epigroup.
(i)J=D in S;
(ii)for a∈S and x∈S1,if aDxa,then aLxa;
(iii)for a∈S and y∈S1,if aDay,then aRay.Letρbe a binary relation on a semigroupS.ρ∞denotes the transitive closure ofρ,andρ∗denotes the congruence onSgenerated byρ.For the latter,explicitly,fora,b∈S,
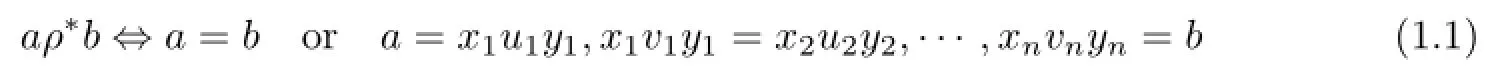
for somexi,yi∈S1,ui,vi∈Ssuch that eitherui(ρ∪∆)viorvi(ρ∪∆)ui,i=1,2,···,n.For anya,b∈S,letζa,bbe the congruence onSgenerated by the singleton{(a,b)}(this denotation dif f ers slightly from that of its original notation introduced in[11]).The radical ofρ,in notationwhich is due to Shevrin,is a relation onSde fi ned by the following condition:
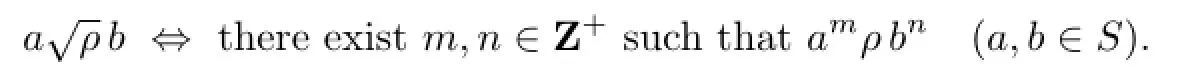
The division relation|and the relation−→onSare def i ned as follows:
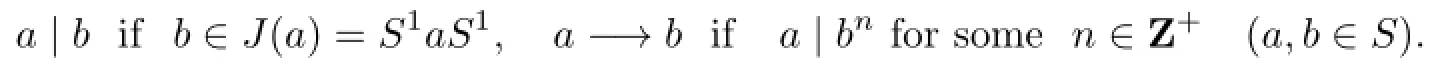
Forn∈N,n≥2,the relation−→nonSis def i ned by
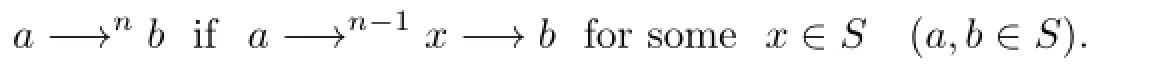
Using the following notation
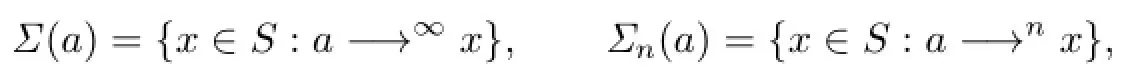
we def i ne the equivalence relationsσandσn(introduced in[12])as follows:
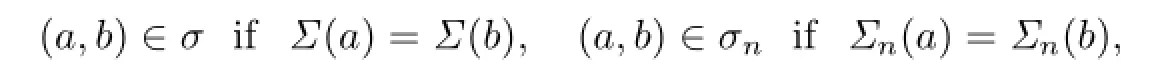
wherea,b∈S,n∈N+.A semigroupSis calledσn-simple ifσncoincides with the universal relation onS.
It is known that forρ,λ∈C(S)such thatρ⊆λ,
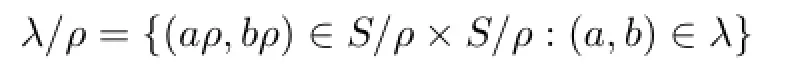
is a congruence onS/ρ,andS/λ≃(S/ρ)(λ/ρ)(see Theorem 1.5.4 in[9]).
LetSbe an epigroup.Forρ∈C(S),the super-kernel(introduced in[6])ofρis the set
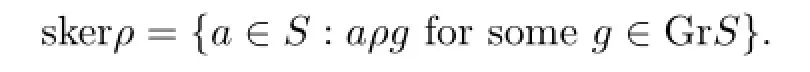
In a simplif i ed version,skerρ={a∈S:aρaaω}.Since,ifaρgfor someg∈GrS,then,from Observation 2.1 in[3],,so thataρaaω.
Lemma 1.2Let S be an epigroup.For ρ∈C(S),
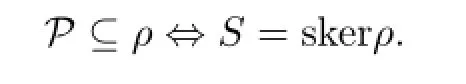
Proof.IfP⊆ρ,then for anya∈S,sinceaPaaω,we haveaρaaωand soa∈skerρ,whenceS⊆skerρ.Conversely,letaPb,that is,aaω=bbω.Then by hypothesisaρaaω=bbωρband soaρb.ThereforeP⊆ρ.This completes the proof.
By def i nition,an epigroupSin which∆isP-congruence-free if and only if forρ∈C(S),
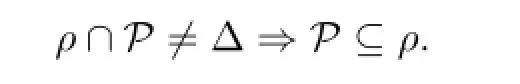
(This statement excludes the casesρ∩P=∆andP⊆ρsimultaneously occur.)We remark that the condition∆inSis equivalent to saying thatShas at least one non-completely regular element.
For an epigroupS,def i ne an equivalence relation P onC(S)by
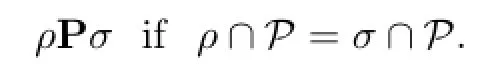
It is easy to see thatSisP-congruence-free if and only if|C(S)/P|≤2(the proof is similar to the ones in[7]and[13]).
Lemma 1.3Let S be an epigroup.
(i)|C(S)/P|=1if and only if S is completely regular;
(ii)|C(S)/P|=2if and only if S has at least one non-completely regular element and for any two distinct elements a,b∈S such that aPb,P⊆ζa,b.
Proof.(i)This equivalence follows immediately from Observation 2.3 in[5],which said that an epigroupSis completely regular if and only ifP=∆inS.
(ii)Leta,b∈Ssuch thatandaPb.Thenζa,b∩P∆.If|C(S)/P|=2,which implies thatSisP-congruence-free and∆,it follows thatP⊆ζa,b.
Conversely,letρ∈C(S)such that∆.Then there exist two distinct elementsa,b∈Ssuch thataρbandaPb.Here at least one ofaandbis a non-completely regular element(otherwise they are equal).Thus from(i)we have|C(S)/P|/1,and by hypothesisP⊆ζa,b⊆ρ.Now we have proved thatSisP-congruence-free and then|C(S)/P|=2.
Lemma 1.4Let S be a P-congruence-free epigroup in which P∆.For any a,b∈SGrS,
(i)aDb;
(ii)Daω∩Da=∅;
(iii)a2∈GrS.
Proof.As we remarked earlier,the condition∆inSimpliesSGr(the converse implication also holds).
(i)Considering the Rees congruenceρJ(a),clearlya(ρJ(a)∩P)aaω,which implies thatρJ(a)∆,then by hypothesisP⊆ρJ(a),and sobρJ(a)bbωsincebPbbω.But, we must haveb(andbbω)∈J(a),that is,J(b)⊆J(a).The reverse inclusionJ(a)⊆J(b)is proved similarly,so thatJ(a)=J(b),that is,aDb.
(ii)Suppose,on the contrary,that.ThenaωDa,while,so from Lemma 1.1aHaω,which,from Corollary 2.2.6 in[9],means thata∈GrS,contradicting the hypothesisGrS.
(iii)If,on the contrary,a2GrS,then from assertion(i)aDa2,which by Lemma 1.1 implies thataHa2,and,from Theorem 2.2.5 in[9],a∈GrS,contradicting the hypothesisGrS.The proof is completed.
We remark that from Lemma 1.4 ifSis aP-congruence-free epigroup,then any noncompletely regular element inS(if it exists)falls into the sameD-class,and,from Lemma 1 in[1],anHaωfor anyn≥2.
Recall,from the Proof of Theorem 1 in[12],that the relationσis the least semilattice congruence on a semigroup.Putcha[14]proved that for any epigroup the transitive closure of(from Lemma 1.1 Green’s relationsJandDcoincide in an epigroup,hence of) is the least semilattice congruence.Also from Corollary 2.7 in[5],the relationP∨Don any epigroup is the least semilattice congruence.
Lemma 1.5Let S be a P-congruence-free epigroup.Then
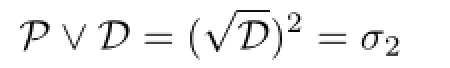
is the least semilattice congruence on S.
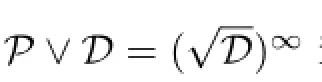
(I)If(n1,n2,n3,n4)=(1,1,∗,∗),(2,2,∗,∗),(∗,∗,1,1),(∗,∗,2,2),where∗denotes an arbitrary number in{1,2},then,by the transitivity ofD,.
(II)If(n1,n2,n3,n4)=(1,2,1,2),(2,1,2,1),(1,2,2,1),(2,1,1,2),we show only the fi rst case and the other cases can be proved similarly.For the fi rst equality,we writeanDx,x2Dy,y2Dbm.Ifx,y∈SGrS,then,from Lemma 1.4(i),xDy,so thatanDy,y2Dbm, which givesIf at least one ofxandyis completely regular,say,x∈GrS(which implies thatxDx2),thenanDy,y2Dbmand also
We have shown that in any case,and therefore,as required. Now we getand so.
As we have mentioned above,σ=P∨D,then,from Lemma 5 in[12],σ2⊆σ,so thatσ2⊆P∨D.For the reverse inclusionP∨D⊆σ2,sinceσ2is an equivalence relation,it suffi ces to prove thatP⊆σ2andD⊆σ2.The latter inclusion follows again from Lemma 5 in[12].For the f i rst inclusion,leta,b∈Ssuch thataPb.We show thataσ2b.Ifa,b∈GrS, thena=band triviallyaσ2b.Ifa,b∈SGrS,then,from Lemma 1.4(i),aDb,and clearlyaσ2bsinceD⊆σ2.Ifa∈SGrSandb∈GrS,thenb=aaω(which impliesa2=b2) and so by Lemma 10 in[12]Σ2(b)⊆Σ2(a).To show the reverse inclusion,letx∈Σ2(a). Then there exists somec∈Ssuch that,i.e.,cn∈J(a),xm∈J(c)forn,m∈Z+.Considering possible behaviors ofc,ifc∈SGrS,then again from Lemma 1.4(i)aDc(that is,J(a)=J(c)).Thereforexm∈J(a),that is,a−→x,whileb2=a2, then we haveb−→a−→x,that is,b−→2xand sox∈Σ2(b).Ifc∈GrS,thencHcnand soJ(c)=J(cn).Thusxm∈J(c)=J(cn)⊆J(a),and a similar argument shows thatx∈Σ2(b).Now we have proved thatΣ2(a)⊆Σ2(b)and thenΣ2(a)=Σ2(b),i.e,aσ2b.Ifb∈SGrSanda∈GrS,the same conclusion holds.Therefore,in any case,P⊆σ2,and soP∨D⊆σ2,as desired.This completes the proof.
LetS(an epigroup)be a semilatticeYof epigroupsSη(η∈Y).For an equivalence relationτonS,such as Green’s relations and the relationP,the restriction ofτtoSηis denoted byτ|Sη,and the equivalence relationτonSηis denoted byτSη.It is clear thatPSη=P|Sη,and ifSηis regular,then,from Proposition 2.4.2 in[9],for anyGof Green’s relationsH,LandR,GSη=G|Sη.
Lemma 1.6Let S be a semilattice Y of epigroups Sη(η∈Y)and ρ∈C(S).
(i)ρ∩P=∆S⇔(∀η∈Y)ρ|Sη∩P|Sη=∆Sη;
(ii)P⊆ρ⇔(∀η∈Y)P|Sη⊆ρ|Sη.
Proof.The proof is closely similar to that of Lemma 2.5 in[7].We only show the assertion (i).The implication“⇒”holds trivially.For the converse implication,leta,b∈Ssuch thata(ρ∩P)b.SinceP∨Dis the least semilattice congruence onS,we must havea,b∈Sαfor someα∈Y,so thata(ρ|Sα∩P|Sα)band by hypothesisa=b;the proof of assertion(i) is completed.
Lemma 1.7If an epigroup S is P-congruence-free,then S is a semilattice Y of σ2-simple epigroups Sηand there exists at most one α∈Y such that P|Sα∆Sα.
Proof.From Lemma 1.5,Sis a semilatticeYof semigroupsSη,where anySηis aσ2-class. Ifa∈Sη,thena2∈Sη;from Lemma 1.4(iii),,so thatThusSηis an epigroup (a subepigroup ofS).Now leta,b∈Sη,thenaσ2b,that is,Σ2(a)=Σ2(b).In other words,
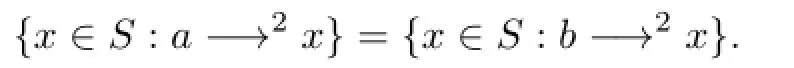
Hence,ifx∈Sηanda−→2xinSη(of course inS),thenb−→2xinS.From Lemma 9(c) in[12],alsob−→2xinSη.We have thus shown that
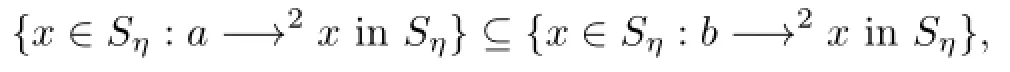
and the reverse inclusion can be proved similarly.Therefore the relationσ2is a universal relation onSη,and thenSis a semilatticeYofσ2-simple epigroupsSη.Thus the f i rst of these statements follows.
The proof of the second is closely similar to that of Lemma 2.6 in[7].This completes the proof.
One more property of P-congruence-free epigroups can now be augmented in Lemma 1.4.
Lemma 1.8Let S be a P-congruence-free epigroup in which P/=∆.Then for any a,b∈SGrS,aωDbω.
Proof.Sincea,b∈SGrS,it follows from Lemmas 1.4 thataDb.Then,and since from Lemma 1.5is the least semilattice congruence onS,we have; hence,for somex∈S,that is,aωDxn,xmDbωforn,m∈Z+.Ifx∈GrS, clearlyaωDbωsincexnDxm.Ifx∈SGr(S),we claim thatn/1 and1,respectively (otherwise,from Lemmas 1.4,aωDxDaandbωDxDb,which gives thata∈GrSandb∈GrS, respectively,contrary to hypothesis).Thusn,m≥2,then,by Lemma 1.4(iii),xn,xm∈GrS, so thatxnHxm.Therefore in any case we haveaωDbω.
2 P-congruence-free Completely 0-simple Semigroups
In this section we turn to deal withP-congruence-free completely 0-simple semigroups,which appears in our principal theorem in the next section.
LetS=M0(I,G,Λ;P)be a completely 0-simple semigroup.Clearly,NilS(=SGrS∪{0}),the singletons{g}g∈GrS{0}are theP-classes ofS,and by means of the Rees matrix representation,they are{(i,g,λ):pλi=0,i∈I,λ∈Λ,g∈G}∪{0},the singletons{(i,g,λ)}forpλi/0.For anyρ∈C(S),we have either 0ρ=Sor 0ρ={0}.In the f i rst caseρ=∇,and in the latter case we shall call it a proper congruence(here|S|≥2).Proper congruences onSare described by means of the following device(see[9],Section 3.5).
Remember that the equivalence relationsEI,EΛonIandΛ,respectively,are def i ned as follows:
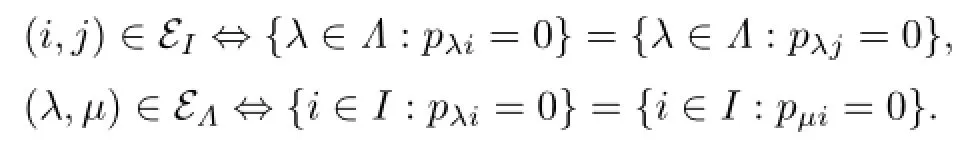
A triple(N,S,T)consisting of a normal subgroupNofG,an equivalence relationSonIand an equivalence relationTonΛis called linked if
(i)S⊆EI,T⊆EΛ;
(ii)ifi,jinIandλ,µinΛare such thatpλi,pλj,pµiandpµjare all non-zero,thenwherever either(i,j)∈Sor(λ,µ)∈T.
We def i ne a relationρ=ρ(N,S,T)onS{0}by
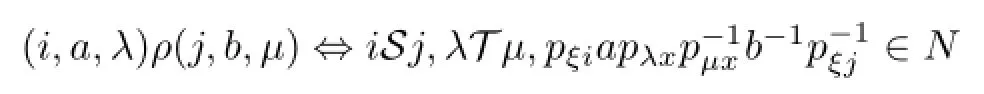
for somex∈Iandξ∈Λsuch thatpξi,pξj,pλxandpµxare all non-zero.Thenρ∪{(0,0)}is a proper congruence onS.Conversely,every proper congruence onScan be so written for a unique linked triple.
Lemma 2.1A completely0-simple semigroup S is P-congruence-free if and only if for any proper congruence ρ on S,ρ∩P=∆.
Proof.Suffi ciency is obvious.For necessity,takeρ∈C(S)with(that is,0ρ={0}). Suppose,on the contrary,that∆.Then there exist two distinct elementsa,b∈Ssuch thata(ρ∩P)b.As we mentioned at the beginning of this section,we havea,b∈NilS. IfSisP-congruence-free,thenP⊆ρand so(noticea,b∈NilS).It follows thatρ=∇,contrary to the hypothesis.Thereforeρ∩P=∆,and the necessity is proved.This completes the proof.
We remark that ifSis a completely 0-simple semigroup with∆inS(that is, NilS{0),then,from Lemma 2.1,SisP-congruence-free if and only if forρ∈C(S)
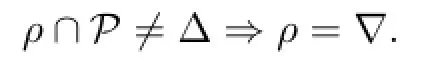
Recall thatSis called to have no proper zero divisors if fora,b∈S,the implication
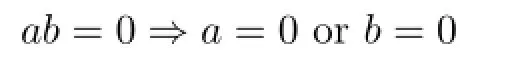
holds.
The next result shows that the classif i cation ofP-congruence-free completely 0-simple semigroups depends on the property of having proper zero divisors.
Proposition 2.2Let S be a completely0-simple semigroup with|S|>2.Then S is P-congruence-free if and only if either
(i)S is a chain Y2of two completely simple components,S0∪S1,where S0={0}and S1=S{0},and in this case,S is completely regular,or
(ii)S=M0(I,{e},Λ;P),where P has entry0,for any distinct λ,µ∈Λ with pλi=0for some i∈I,there exists j∈I such that pλjpµj,and for any distinct i,j∈I with pλi=0for some λ∈Λ,there existsµ∈Λ such that pµipµj.
Proof.IfShas no proper zero divisors(that is,NilS={0}),thenS{0}is a(completely simple)subsemigroup ofSandSis completely regular.For the converse,sinceSis completely regular,clearlySisP-congruence-free.
Assumed thatS=M0(I,G,Λ;P)has proper zero divisors,say,Phas entrypλi=0 for somei∈I,λ∈Λ.Now the triple(G,∆I,∆Λ)is linked and gives rise to a proper congruenceρ(G,ΔI,ΔΛ)onS.Then for anyg1,g2∈G,since(i,g1,λ),(i,g2,λ)∈NilS,we have((i,g1,λ),(i,g2,λ))∈ρ(G,ΔI,ΔΛ)∩P.IfSisP-congruence-free,then by Lemma 2.1 (i,g1,λ)=(i,g2,λ),consequentlyg1=g2,which implies thatG={e};hence({e},EI,EΛ) is also a linked triple and determines a proper congruenceρ({e},EI,EΛ).Here at least one of|I|,|Λ|has more than one element(otherwise|S|=2,in this case,S={(1,e,1),0},contradicting the hypothesis).We assume that|Λ|>1.Takingµ∈Λ,if(λ,µ)∈EΛ,thenpµi=0 and so((i,e,λ),(i,e,µ))∈ρ({e},EI,EΛ)∩P.Thus,using Lemma 2.1,we getλ=µ. If(λ,µ),by def i nition ofEΛ,rowsλandµare not identical,since any entry ofPiseor 0.Now we have proved that the rowλwith entry 0 has no other identical row.The conclusion of columns can be checked similarly.
Conversely,if(ii)holds,then the linked triple({e},EI,EΛ)determines the largest proper congruence onS.For the desired conclusion,according to Lemma 2.1,it is enough to show thatρ({e},EI,EΛ)∩P=∆.Let((i,e,λ),(j,e,µ))∈ρ({e},EI,EΛ)∩P.Ifpλi=e,pµj=e,then (i,e,λ),(j,e,µ)∈GrS,and so(i,e,λ)=(j,e,µ).Since neither the casespλi=e,pµj=0 nor the casepλi=0,pµj=ecan occur(otherwise in either case they cannot fall in the sameP-class),we remain to show that ifpλi=0,pµj=0,then(i,e,λ)=(j,e,µ).Since (λ,µ)∈EΛ,it follows that rows(with entry zero)λandµare identical,then by hypothesis we haveλ=µ.Similarly,we geti=jand thus(i,e,λ)=(j,e,µ),as required.
3 P-congruence-free Epigroups
Now it is time for us to give the main result in this paper,which characterizeP-congruencefree epigroups,whereP-congruence-free completely 0-simple semigroups occur as one of special cases,since they are in hand in the previous section.
Theorem 3.1Let S be an epigroup.Then S is P-congruence-free if and only if either
(i)S is completely regular,or
(ii)S is a semilattice Y of σ2-simple epigroups Sηand Sηare completely simple semigroups for all η∈Y but one α∈Y such that Sα=D∪I,where D=Da,I=Da2for any a∈SGrS and I is the completely simple kernel of Sα.Additionally,one of the following conditions holds:
(iia)Sαhas only one non-completely regular element;
(iib)Sαhas more than one non-completely regular element and exactly two principal factors,J/I,I,where,and J/I is a P-congruence-free completely0-simple semigroup(with order more than two);
(iic)Sαhas more than one non-completely regular element,and for any distinct a,b∈SGr(xay∈D⇔xay∈D);
(iic-1)if for any a∈SGrS,|aP|=2,then either Sαis P-congruence-free or for any distinct a,b∈SGr(β,γ≥α)such that a=xby,where β>α or γ>α;
(iic-2)if there exists some a∈SGrS,|aP|>2,then for any distinct a,b∈SGrS such that aPb,there exist(β,γ≥α)such that xay∈D,xby∈I,or xby∈D, xay∈I,where β>α or γ>α.
Proof.Necessity.IfSisP-congruence-free,then,from Lemma 1.7,Sis a semilatticeYofσ2-simple epigroupSη,and either
(1)for anyη∈Y,P|Sη=∆Sη,then,from Observation 2.3 in[5],Sαis completely regular and soSis completely regular,or
(2)there exists anα∈Ysuch thatand for any otherη∈Ywith=∆Sη.
IfP|Sη=∆Sηforη∈Y,that is,Sηis completely regular,then for any(completely regular elements)a,b∈Sη,from Lemma 1.5,,that is,aDxn,xmDbfor somex∈S.Then,by Lemma 1.5,xn,xm∈Sη,so that they are all completely regular,which givesxnDxmand thenaDb.Alsoab∈Sη.We similarly getaDabDb,and then from Lemma 1.1 we haveaRabLb.SinceSηis a(completely)regular subsemigroup ofS,from Proposition 2.4.2 in[9],we getaRSηabLSηb,so thataDSηb.In this case,Sηis completely simple.For the only oneα∈Y,since,there exist two distinct elementsa,b∈Sαsuch thataPb, which means that at least one ofa,b,say,ais a non-completely regular element(otherwisea=b,contradicting the distinction of them).In this case,sincea2Haω,by Lemma 1.4,we have.For anys∈Sα,ifs∈SGrS,then from Lemma 1.4s∈Da;ifs∈GrS, we say thats∈Daors∈Da2.For the latter claim,we give its explanation in the following. Sincea2,s∈GrSα,by Lemma 1.5,we have,that is,sDxn,xmDa2for somex∈Sandn,m∈{1,2}.Here ifx∈GrS,thensDa2.Ifx∈SGrS,n=1,thensDxDaand sosDa;ifn=2,then from Lemma 1.8sDx2Da2and sosDa2.Now we have shown thatSα⊆Da∪Da2,while from Lemma 1.5Da∪Da2⊆Sα,soSα=Da∪Da2.We denoteDaandDa2byDandI,respectively.Since from Lemma 1.4 all non-completely regular elements fall inD,it follows that any element inIis completely regular.Next,we show thatIis the two-sided ideal ofSαgenerated bya2,that is,Ifb∈I,that is,bDa2,thenb∈Sαandb=xa2yfor somex∈Sβ,y∈Sγ,whereβ,γ≥α(sincea2,b∈Sα). Notice thata2is completely regular andaω∈Sα,hence.Thus we have.For the reverse inclusion,sinceand, it is easy to see that(otherwise,aDa2,which implies thata∈GrS, contradicting the hypothesisa∈SGrS).Furthermore,ifMis an ideal ofSαsuch thatM⊆I,then for someb∈M,alsoand so(notice thatI=Da2,it is routine to check.Now
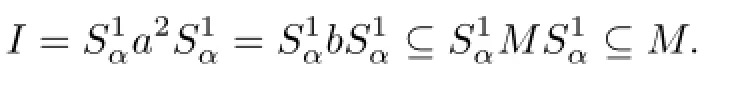
Therefore,Iis the simple kernel(that is,the minimal ideal)ofSαand thus the completely simple kernel ofSαsince any element inIis completely regular.
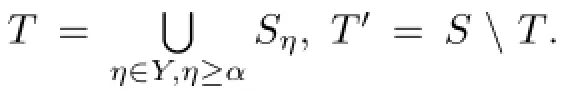
We consider the following possibilities:
Case 1.Shas only one non-completely regular element,that is,|SGrS|=1.
Case 2.|SGrS|≥2.
Case 2.1.For any distincta,b∈SGrS,there existsuch thatxay∈D,xby∈I,orxby∈D,xay∈I.
In this case,we claim thatS0has exactly two principal factorsJ/I,I,whereJ=S0, andJ/Iis aP-congruence-free completely 0-simple semigroup(clearly with order more than two).
Here the casex=y=1 cannot occur(otherwiseaorbin GrS,contradicting the hypothesisa,b∈SGrS).Thus at least one ofx,y,say,x∈S0,more accuratelyx∈D, then we must havexaorxbinDsincexayorxbyinD.Now from Propositions 2.3.1 and 2.3.7 in[9]Dis regular and thenS0(whenceS)is regular.Letb,c∈S0such thatbDc. Then there existu1,v1,u2,v2∈S1such that
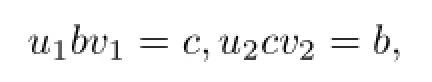
so,for someb′∈V(b)⊆S0(the inclusion follows from the fact thatb′Db),we havec= (u1bb′)b(b′b)v1and thenc∈S0bS0.Similarly,b∈S0cS0and sobDS0c.We have shown thatD|S0⊆DS0and clearlyD|S0=DS0since the reverse containment is obvious.Therefore we may say thatDbinSis equal toDbinS0sinceDb⊆S0.Also as we have just proved in the preceding along with,S0is a principal two-sided ideal ofSαgenerated by one(any)non-completely regular elementa,that is,(we remark that hereS0=SaSsince we have setS=T).
InS0,recall the notationI(a)={x∈S0:Jx<Ja}.It is clear thatI(a)=I,Ja=DandS0=J(a)=S0aS0.Thus we say thatS0has exactly two principal factorsJ/IandI(this is not true ifSis not regular sincein this case),and from Lemma 1.3.14 in [8]these two principal factors are all completely 0-simple.In fact,as we have mentioned,Iis completely simple.Next we show thatJ/I(actually,S0/ρI)isP-congruence-free.From Lemma 2.1,forσS0/ρI∈C(S0/ρI)with,it suffi ces to show thatσS0/ρI=∇.
Since,we have(cρI)P(dρI),(cρI)σS0/ρI(dρI),,for somec,d∈S0.Ifcanddare all completely regular sincecρIPdρI,thencρI=ccωρI=ddωρI=dρI,and socρId,contradicting.Thus at least one ofcandd,say,cis non-completely regular.In this case,ifd∈GrS0,then we have(cρI)σS0/ρI(ccωρI).Thus we getσS0/ρI=∇since for a non-trivial completely 0-simple semigroup,ifρis a congruence on it with,thenρis the universal congruence(see Section 3.5 in[9]).Ifcanddare all non-completely, then by hypothesis there existsuch thatxcy∈D,xdy∈I(orxdy∈D,xcy∈I, in this case,it can be proved similarly).SincecDxcyandD|S0=DS0as just mentioned,we havec=uxcyvfor someu,v∈S0.Therefore,cρI=((uxcyv)ρI)σS/ρI((uxdyv)ρI),whereas (uxdyv)ρI∈GrS/ρI,which means(cρI)σS/ρI(ccωρI).ThusσS0/ρI=∇.
Case 2.2.For any distincta,b∈SGrS,,
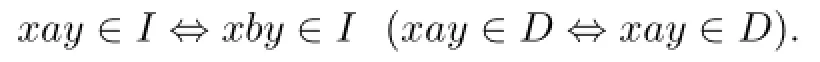
Case 2.2.1.For anya∈SGrS,|aP|=2.
(1)Dis not regular.
In this case,for anya,b∈SGrSsuch that,then,from Lemma 1.4,there exist(β,γ≥0)such thata=xby.Here we claim that at least one ofβ,γis larger than 0.Otherwise,β=0,γ=0.Clearly the casex=y=1 cannot occur,then at least one ofx,y,say,1.Sincea∈D,we havex,by∈D(otherwise at least one of them is inI,and so doesa,a contradiction).Nowx,by∈D,whilexby=a∈D,then from Propositions 2.3.1 and 2.3.7 in[9],Dis regular,contradicting the condition thatDis not regular.
(2)Dis regular.
In this caseSis regular and we claim thatS0isP-congruence-free.
Firstly,sinceSisP-congruence-free,by Lemma 1.3,P⊆ζa,aaωfor anya∈SGrS,and thus.We show that.Since the inclusionis obviously true,it suffi ces to show that.Letb,c∈S0such thatandThen from(1.1),
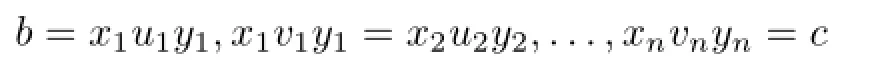
for somexi,yi∈S1,ui,vi∈Ssuch that(ui,vi)∈{(a,a),(a,aaω),(aaω,a),(aaω,aaω)},i=1,2,···,n.Sinceais regular,we have
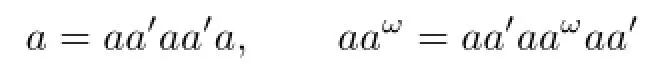
for somea′∈V(a),and then
b=(x1aa′)u1(a′ay1),(x1aa′)v1(a′ay1)=(x2aa′)u2(a′ay2),···,(xnaa′)vn(a′ayn)=c,wherexiaa′,a′ayi∈S0,ui,vi∈S0,so thatb(ζa,aaω)S0c.Thusζa,aaω|S0⊆(ζa,aaω)S0,as required.
NowPS0=P|S0⊆ζa,aaω|S0=(ζa,aaω)S0(note that here|aP|=2),and from Lemma 1.3S0isP-congruence-free.
Case 2.2.2.For somea∈SGrS,|aP|>2.
In this case,we say that for any distincta,b∈SGrSsuch thataPb,there exist(β,γ≥0)such thatxay∈D,xby∈I,orxby∈D,xay∈I,whereβ>0 orγ>0. Otherwise,for anyx,y∈S,
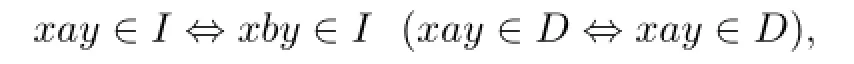
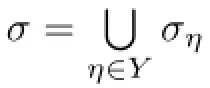
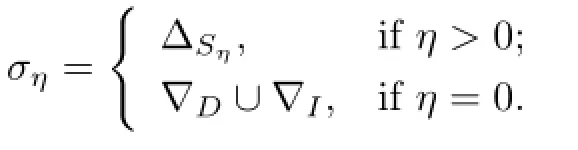
It is clear thatσis a congruence onSanda(σ∩P)b.Thus∆,and,by the hypothesis thatSisP-congruence-free,P⊆σ,soaσaaωsinceaPaaω.But from the def i nition ofσ, (a,aaω),a contradiction.
Suffi ciency.A completely regular semigroup is clearlyP-congruence-free.Assume thatSsatisf i es the conditions of the f i st part of(ii).We note thatSGrS⊆DsinceSGrS⊆Sα=D∪I,whereasIis completely regular.We show that ifSadditionally satisf i es one of the conditions(iia)–(iic),thenSisP-congruence-free.
IfSsatisf i es(iia),it is easy to see thatSisP-congruence-free.In fact,for this noncompletely regular element,say,a,theP-class containingais{a,aaω},and all the otherP-classes have only one element.Thus for anyρ∈C(S),either(a,aaω)∈ρ,which implies thatP⊆ρ,or(a,aaω),which implies thatρ∩P=∆.
IfSsatisf i es(iib),we claim thatSαis alsoP-congruence-free.Thus from Lemma 1.6SisP-congruence-free.In the following we show thatSαisP-congruence-free.
Note f i rst that for anya,b∈SGrS,sinceSαhas exactly two principal factors,we haveJ1/I=J2/I,whereand then,from Proposition 1.7.1 in[9],,that is,aDSαb.If,that is,Dhas a completely regular element (thus having an idempotent),thenDis regular and soSαis regular.If,on the contrary,SGrS=D,clearly,then for anyaDSαb,we must haveab∈I(otherwise,a,b∈D⇒ab∈D,then,from Propositions 2.3.1 and 2.3.7 in[9],Dis regular,contradicting the hypothesisSGrS=D).ThusSα/ρIis a null semigroup, contradictingSα/ρIbeing completely 0-simple.So far,we have seen thatSαis regular,and as we mentioned in the proof of Case 2.1,here alsoDSα=D|Sα,and thusTo show thatSαisP-congruence-free,for anyρ∈C(Sα),if∆,we show thatP⊆ρ. From Lemma 1.2,it suffi ces to prove that for anya∈SαGrSα(=SGrS,actually),aρaaω.Since∆,there exist two distinct elementsb,cinSαsuch thatbρc,bPc,which means that at least one ofb,c,say,bis a non-completely regular element.Clearly here (bρI)(P∩(ρ∨ρI)/ρI)(cρI)sinceb(ρ∨ρI)candbρIcρI(otherwiseb=c,contradicting their distinction,or each of them is inIand thus completely regular,contradicting the fact that one of them is non-completely regular).Thus by Lemma 2.1 we get(ρ∨ρI)/ρI=∆inSα/ρIsinceSα/ρIisP-congruence-free completely 0-simple.Now for any non-completely regular elementa∈Sα,we have(aρI)((ρ∨ρI)/ρI)(aaω),that is,a(ρ∨ρI)aaω.Then,for somen∈N,there exist elementsx1,x2,···,x2n−1inSαsuch that
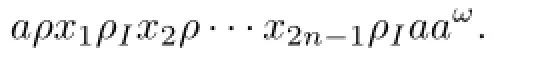
Now ifx1∈GrSα,we geta∈skerρ;ifx1GrSα,we getx1=x2.Then,by induction, we arrive at eithera∈skerρ,or f i nallyaρx2n−1ρIaaω.In the latter,clearlyx2n−1∈GrSαsince thataaω∈Iimpliesx2n−1∈I,and thena∈skerρ.
IfSsatisf i es(iic),for the f i rst case,ifS0isP-congruence-free,then from Lemma 1.6SisP-congruence-free;if for any distincta,b∈SGrS,there exist(β,γ≥α) such thata=xby,whereβ>αorγ>αand|aP|=2,we show thatSisP-congruence-free. Letρ∈C(S)such that∆.Then there existc,d∈Ssuch thatc(ρ∩P)dand. Thus eitherc∈SGrS,d∈GrS,ord∈SGrS,c∈GrS(notice that since|cP|=2,thecasec,d∈SGrScannot occur).We assume thatc∈SGrS(here,d=ccω;the other case can be proved in a similar manner),then we havecρccω.Now lettinga∈SGrS,then by hypothesis there existx,y∈Ssuch thata=xcyand soa=xcyρxccωy,whilexccωy∈I, which impliesaρaaω.Now we have proved thatS=skerρ.Thus by Lemma 1.2P⊆ρandSisP-congruence-free.
For the second case,suppose that forρ∈C(S)such that∆.Then there existc,d∈Ssuch thatc(ρ∩P)dand.Sincec,d∈GrScannot occur(otherwise they are equal),we have the following three possibilities:c∈SGrS,d∈GrS;d∈SGrS,c∈GrS;c,d∈SGrS.Ifc∈SGrS,d∈GrS(here,d=ccω;the second case can be proved in a similar manner),then we havecρccω.Now for anya∈SGrS,as we mentioned at the beginning of the proof of Suffi ciency,aDcand then,for someu,v∈S1,a=ucvρuccωv,whileuccωv∈I(notice thatucv=a∈Sα;thenu∈Sβ,v∈γwhereβ,γ≥α,so thatuccω∈Sα), which impliesaρaaω.Ifc,d∈SGrS,then by hypothesis there existx,y∈Ssuch thatxcy∈D,xdy∈I,orxdy∈D,xdy∈I,say,xcy∈D,xdy∈I,so that for anya∈SGrS, sinceaDxcy,there exist someu,v∈S1,a=uxcyvρuxdyv,whileuxdyv∈I,which impliesaρaaω.HenceSGrS⊆skerρ.Thus by Lemma 1.2P⊆ρandSisP-congruence-free.
[1]Shevrin L N.On the theory of epigroups,I.Russ.Acad.Sci.Sb.Math.,1995,82:485–512.
[2]Shevrin L N.On the theory of epigroups,II.Russ.Acad.Sci.Sb.Math.,1995,83:133–154.
[3]Shevrin L N.Epigroups.in:Kudryavtsev V B,Rosenberg I G(eds.).Structural Theory of Automata,Semigroups,and Universal Algebra.Berlin:Springer,2005:331–380.
[4]Liu J G.Epigroups in which the operation of taking pseudo-inverse is an endomorphism.Semigroup Forum,2013,87:627–638.
[5]Liu J G.Epigroups in which the relation of having the same pseudo-inverse is a congruence.Semigroup Forum,2013,87:187–200.
[6]Liu J G.A relation on the congruence lattice of an epigroup.Adv.Math.(China),2014,43: 496–504.
[7]Yu H,Wang Z,Wu T,Ye M.Classif i cation of someτ-congruence-free completely regular semigroups.Semigroup Forum,2012,84:308–322.
[8]Higgins P M.Techniques of Semigroup Theory.Oxford:Oxford University Press,1992.
[9]Howie J M.Fundamentals of Semigroup Theory.Oxford:Clarendon,1995.
[10]Clif f ord A H,Preston G B.The Algebraic Theory of Semigroups,Vol.II,Mathematical Surveys,No.7.,Providence:American Mathematical Society,RI,1967.
[11]Petrich M.The kernel relation for a completely regular semigroup.J.Algebra,1995,172: 90–112.
[12]´Ciri´c M,Bogdanovi´c S.Semilattice decompositions of semigroups.Semigroup Forum,1996, 52:119–132.
[13]Liu J G,Kong X Z.Completely regular semigroups for which|C(S)/L|≤2.J.Math.Study, 2005,38:227–230.
[14]Putcha M S.Semigroups in which a power of each element lies in a subgroup.Semigroup Forum,1973,5:354–361.
tion:20M10
A
1674-5647(2017)02-0097-13
10.13447/j.1674-5647.2017.02.01
Received date:Oct.8,2014.
Foundation item:The NSF(ZR2010AL004)of Shandong Province of China.
E-mail address:liujingguo@lyu.edu.cn(Liu J G).
 Communications in Mathematical Research2017年2期
Communications in Mathematical Research2017年2期
- Communications in Mathematical Research的其它文章
- Some Topological Properties of Charming Spaces
- Boundedness in Asymmetric Quasi-periodic Oscillations
- A New Characterization on g-frames in Hilbert C∗-Modules
- Growth of Solutions to Higher Order Dif f erential Equation with Meromorphic Coeffi cients
- Uniqueness in Determining a Ball with a Single Incoming Wave
- Two Bijections on Weighted Motzkin Paths
