Liu混沌系统的参数识别自适应同步

魏炎炎,周海攀

Liu混沌系统的参数识别自适应同步

魏炎炎,周海攀

（云南经济管理学院,云南昆明650304）

以Liu系统的混沌现象为例,画出一个混沌吸引子相图,讨论Liu混沌系统自同步的问题.研究Liu混沌系统的自适应同步和响应系统参数识别,利用参数识别自适应控制技术,设计非线性控制器,找出参数自适应律、控制器系数的范围,同时提出了控制增益.借助Lyapunov稳定性理论及LaSalle不变集原理,给出了响应系统参数识别的充分条件,并通过数值仿真验证了所给方法的真实有效性.

混沌系统；混沌同步；参数识别；非线性控制器；自适应同步

混沌同步的研究范围涉及保密通信、电子线路、信息科学等领域.20世纪末,Mainieri和Rehacek发现一种新的混沌系统同步现象,即投影同步[1],驱动系统及响应系统的对应变量按照固定的比例关系进行演化,这是一类特殊广义的同步现象,这种广义同步形式迅速成为研究混沌同步的焦点[2-6].目前,关于参数识别的混沌同步的研究主要聚集在驱动系统中参数的识别,响应系统中的参数识别的研究相对较少.

1 系统的提出

Liu混沌系统是一个连续的三维的自治系统,数学模型表示如下

式（1）中：x、y、z是状态变量,a、b、c、k、h为系统的参数,当a=10,b=40,c=2.5,h=4,k=1时,Liu系统处于混沌的状态,若选取初始值（x,y,z）=（1,2,3）,系统出现一个吸引子,如图1、图2所示.

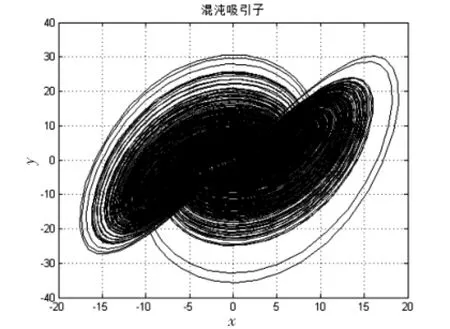
图1 x-y投影Fig.1 Plane projection

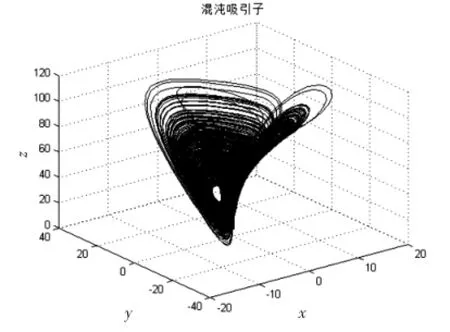
图2 x-y-z相图Fig.2 Chaotic attractor

2 Liu混沌系统的参数识别自适应同步

2.1 问题描述

现考虑驱动和响应系统

2.2 Liu混沌系统同步

现考虑驱动系统（3）和响应系统（4）

式（3）、式（4）中,a、b、c、h、k为驱动系统已知参数,a1、b1、c1、h1、k1为响应系统未知参数,由误差e= y−λ x（λ为非零常数）,可以得出误差系统方程

若采取下列控制器

式（6）中：q＞0为控制增益,l为控制器系数.

可知,参数自适应律为

式（7）中：pa、 pb、 pc、 ph、 pk是对参数a1、 b1、 c1、 h1、 k1的估计值.

定理若,在控制器（5）及参数自适应律（7）下,则驱动系统（3）及响应系统（4）实现广义同步,即对任意初值,未知参数并且能够被识别,即

证明：控制器（6）代入误差方程（5）得

考虑Lyapunov函数

对（9）式求导得

ei→0( i=1,2,3),得到了系统（3）和系统（4）实现广义同步,同时pa→ a1, pb→ b1,pc→ c1, ph→ h1, pk→ p1,从而未知参数a1, b1, c1, h1, k1被识别.证毕.

3 数值仿真

根据上述理论分析,通过MATLAB软件进行模拟,采用4阶龙格—库塔方法进行计算,对驱动和响应系统进行仿真,现选取原系统参数a=10, b=40, c=2.5, h=4, k =1,响应系统未知参数随意选取一组数值a1=9.5, b1=40.2, c1=2.3, h1=4.2, k1=1.2,其估计值初始分别取pa(0)=8.5, pb(0)=37, pc(0)=0.1, ph(0)=2.5,pk(0)=-1,取q=10,任选取驱动系统及响应系统的初始值分别为x(0)=[1,2,3]T, y(0)=[8,20,10]T,取控制器的系数l=70,取λ=1,其误差e1、 e2、 e3如图3,未知参数a1、 b1、 c1、 h1、 k1识别如图4.

图3 误差e1、e2、e3Fig.3 Error e1、e2、e3

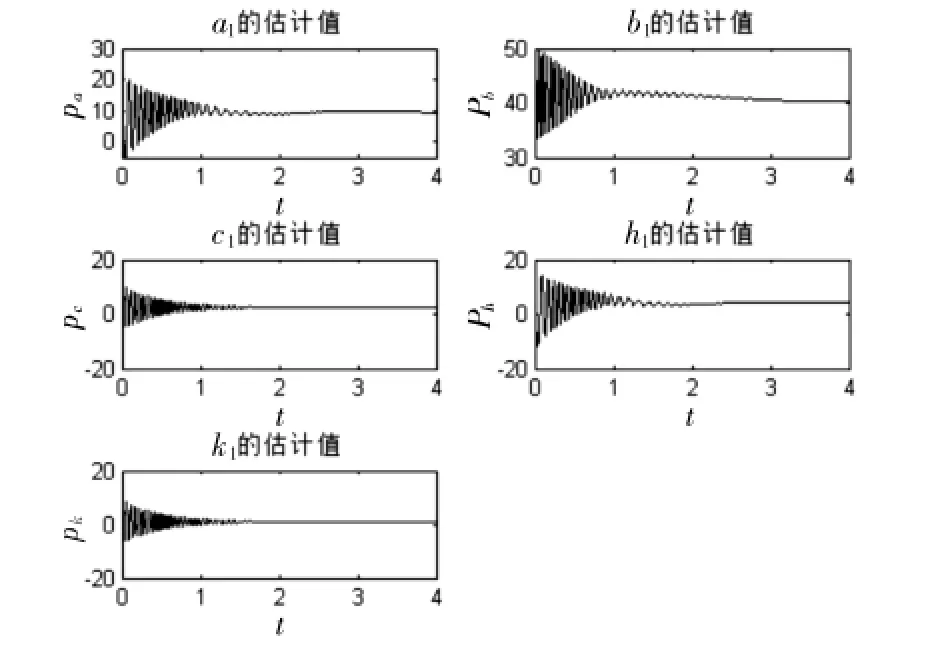
图4 a1、b1、c1、h1、k1估计值Fig.4 Estimated value of a1,b1,c1,h1,k1

由图3、图4可知,在控制器（6）及参数自适应律（7）下,则驱动系统（3）及响应系统（4）实现广义同步,且能够被识别未知参数.

4 小结

本文主要基于Liu混沌系统,通过参数识别自适应控制技术,使原本不匹配的两个参数在全局范围内实现广义同步.本文给出的参数自适应律和控制器简单有效,且收敛的速度较快,在实际应用中具有很好的参考及应用价值.

[1]MAINIERIR,REHACEK J.Projective synchronization in three-dimensional chaotic systems[J].Phys.Rev.Lett.,1999,82（15）：3042-3045.

[2]刘秉正,彭建华.非线性动力学[M].北京：高等教育出版,2004：44-46.

[3]陈彦飞.混沌系统的自适应同步与参数识别[D].桂林：桂林理工大学,2013：19-24.

[4]魏炎炎.超Rabinovich系统混沌现象及混沌同步的研究[D].西安：西安建筑科技大学,2012：38-42.

[5]潘光,魏静.一种分数阶混沌系统同步的自适应滑模控制器设计[J].物理学报,2015（4）：505-510.

[6]LASALLE J P.The extent of asymptotic stability[J].Proceedings of the National Academy of Sciences of the United States of America,1960,46：363-365.

（责任编辑：卢奇）

Parameter identification adaptive synchronization of Liu chaotic system

WEIYanyan,ZHOU Haipan
（Yunnan College of Business Management,Kunming 650304,China）

A chaotic phenomena of the Liu system is studied,and a chaotic attractor of the system is draw.Then, adaptive synchronization of Liu chaotic system is discussed.And adaptive synchronization and parameter identification of response system problems of a class of Liu chaotic system are studied.Parameter identification adaptive control technology is used.The nonlinear controller is designed,the parameter adaptive law and the scope of the controller coefficient are foud out.And the control is given by Lyapunov stability theory and principles of LaSalle invariant set.So the sufficient condition of the parameter identification of response system is given.The method given in this paper is real validity by numerical simulation.

chaotic systems；chaotic synchronization；parameters identification；nonlinear controller；adaptive synchronization

O415.5

A

1008-7516（2017）02-0054-04

10.3969/j.issn.1008-7516.2017.02.012

2016-11-12

魏炎炎（1984―）,女,湖北随州人,硕士,讲师.主要从事非线性动力学方向研究.