基于分形理论的察尔森灌区渠系水利用效率分析

黄永江，屈忠义，邵忠继

(1.内蒙古农业大学水利与土木建筑工程学院， 内蒙古 呼和浩特 010018；2.内蒙古察尔森灌区管理局， 内蒙古 乌兰浩特 137400)

基于分形理论的察尔森灌区渠系水利用效率分析

黄永江1，屈忠义1，邵忠继2

(1.内蒙古农业大学水利与土木建筑工程学院， 内蒙古 呼和浩特 010018；2.内蒙古察尔森灌区管理局， 内蒙古 乌兰浩特 137400)

为研究灌区渠系布置结构和渠系水利用效率之间关系，更合理指导灌区进行渠系节水改造和灌溉管理，应用分形理论对察尔森灌区各灌域渠系布置结构与渠系水分利用效率进行评价，根据察尔森灌区现状渠系资料，采用Horton河系定律计算了各灌域的分形维数(好田1.3，义勒力特3.6，乌兰哈达2.5，斯力很1.6，国光1.7，哈达那拉1.8)，在此基础上，结合2013—3014年实际测算数据，分析了各灌域的分维数和渠系水利用效率的关系。结果表明：各灌域渠系水利用效率与分维数之间基本呈大开口抛物线，随分维数(D)增大，渠系水利用效率先减小后增大；察尔森灌区各灌域可通过适当降低分维值以提高渠系水利用效率；未来通过减少斗渠长度同时增加支渠数目与长度的措施是察尔森灌区提高渠系水利用效率的方向之一。

察尔森灌区；Horton河系定律；渠系水利用效率；分形维数

在地表水灌区中，渠系水利用效率对灌溉水利用效率和灌区总引水量有较大影响，然而，目前我国地表水灌区平均渠系水利用效率仍较低，渠系节水潜力仍然很大，因此，需要全面分析影响渠系水利用效率的相关因素，寻求切实可行的办法，以提高渠系水利用效率，这对指导地表水灌区渠系进行合理改造具有重要现实意义。

目前，对于渠系水利用效率的影响因素研究主要集中在渠道过水流量、渠床土质以及渠道衬砌[1-3]等因素，而从渠系布置结构方面开展的研究相对较少。基于分形理论的Horton定律能合理表征河流水系结构特征。自从20世纪40年代Horton等提出Horton定律以来，国内外众多学者对河系形态开展了大量研究，并对Horton定律进行了不断修正[4-9]，目前，Horton定律是一种可以比较准确地反映河网水系结构特征分维的理论。而灌区渠系同自然界自组织形成的分形系统(如水系等)具有很多相似之处，是遵从自然规律和分形体系特征的客观反映。但对于经过人工改造的灌区渠系结构的Horton表征方法，国内研究较少。贺军奇等[10]研究了渠系水利用效率与渠道密度之间的关系并建立了数学模型，为评价渠系布置结构的合理性提供了参考依据；王小军等[11-12]研究了分形理论在广东省灌区渠系布置中的应用；刘丙军等[13]进行了漳河灌区渠系分形的特征研究。屈忠义等[14]研究了河套灌区渠系水利用效率与分维值之间的关系，这些研究成果均表明了Horton定律在灌区渠系结构方面应用的合理性。但以上研究，主要针对渠系结构较完善灌区的同一级别渠系布置结构与渠系水利用效率、灌溉水利用效率之间的关系进行分析，而对存在越级取水，各灌域渠系级别存在差异的灌区，并未进行深入研究。基于此，本文以内蒙古兴安盟察尔森灌区为研究对象，应用分形理论对察尔森灌区各灌域不同类型渠系布置结构(包括存在越级取水的渠系)和渠系水利用效率之间的关系进行研究，通过计算渠系特征参数(如长度比、分枝比等)和分维数，分析评价察尔森灌区现状渠系布置结构的合理性，从提高渠系水利用效率角度出发，确定合理渠系特征参数与分维数，寻求相对最佳的渠系布置结构，为察尔森灌区未来提高渠系水利用效率，合理进行渠系节水改造提供指导。

1 Horton河系定律及特征参数

河流水系的的结构特征具有自然和谐的空间秩序，符合自然结构的合理性，因此可以用Horton定律来计算。反映河流水系结构特性的特征参数有河网密度、河系发育系数、河系不均匀系数、河频数、分枝比、长度比、水面率、河网复杂度、河网发展系数及河网结构稳定度等指标，其中主要包括分枝比和长度比[15]。

分形维数反映了物体占有空间的有效性。分形几何学发明之后，部分学者开始投入到寻求Horton水系定律和分形理论之间的相互联系的研究[16]，20世纪80年代末期，经过La Barbera和Rosso等分析与研究，Horton-Strahler定律以及Hack定律所隐含的分形规律得到了比较确切的表述：即主要通过河流水系的分枝比(Rb)和长度比(Rl)来计算河网分维数(D)[17]。Horton的研究认为，同一流域内河流的数目(N)、长度(L)等水系结构特征参数随着河道级别的不同而呈现几何级数的变化[18]，即：

(1)

(2)

式中，Rb为河流水系分枝比；Rl为河流水系长度比；ω为河流级别序号；Q为河流最高级别；Nω为第ω级河流的数目；L1、Lω：分别为第1、ω级河流的平均长度，单位为(km)。

以ω为横坐标计算得到的直线斜率绝对值的反对数分别来表示Rb和Rl的值，即：

(3)

式中，Rx为水系结构参数(x=b,l)；kx(x=b,l)为ω—lgNω与ω—lgLω回归直线的斜率。Rb一般在3～5之间；Rl一般在1.5～3之间[13，19]。

Horton认为流域内不同等级水系的发育具有自相似特征，国内外学者就水系分维以及流域地貌特征开展了相关研究[20]，建立了分维值与水系特征参数间的关系。La Barbera和Rosso给出的水系分维数D计算式[17]为：

D=1gRb/1gRl

(4)

Barbera等[21]认为水系分维数应在1～2之间，平均值为1.6～1.7，Tarboton等计算出的分维数D值在1.7～2.5之间[12]。水系分维数越大说明水系越复杂，反之则越简单。

2 察尔森灌区概况

察尔森灌区位于内蒙古自治区东部兴安盟境内洮儿河的河谷平原中，北起察尔森水库坝下科尔沁右前旗察尔森镇，南至吉林省白城地区边界，东西两翼为低山丘陵区，灌区南北长74 km，东西宽2～15 km，地理坐标为东经121°51′～122°35′，北纬46°26′～45°45′。灌区年平均降水量408 mm，年平均蒸发量1 836～1 960 mm，多年平均引水量为4.215亿m3，灌区由好田、义勒力特、乌兰哈达、斯力很、国光、哈达那拉、生态草原等七个灌域组成，现有总干渠6条，干渠16条，支渠7条，斗渠212条，各类渠系建筑物194座，经过多年建设，灌区渠系工程状况较好，渠道衬砌率高。灌区总土地面积75 313 hm2，总耕地面积34 706 hm2，草场面积31 866 hm2。

3 察尔森灌区渠系特征参数及分形维数计算

以内蒙古自治区水利厅内蒙古东部大型地表水灌区灌溉水效率测试与评估项目2013—2014年渠道测试结果与计算数据以及其他统计数据为依据(见表1)，按照从水源引水的次序对渠系进行分级，并利用公式(1)～(4)来计算渠系的分维数，计算结果见表2。

表1 察尔森灌区渠系基本情况及测算结果

表2 察尔森灌区渠系特征参数及分形维数计算结果

4 结果分析

4.1 渠系特征参数

已有研究证明：河流水系分枝比取值在3～5之间，长度比取值在1.5～3之间，分维数取值在1～2.5之间比较合理；王小军[11-12]等认为四级渠系以上的灌区存在水系分维特征，其他低级类型灌区渠系并不存在严格意义上的水系分维特征。但其作为表征灌区渠系形态的重要综合指标，可为分析渠系水利用效率提供一个新途径。

由上表计算结果可知：察尔森灌区除乌兰哈达和国光灌域外其它灌域的分枝比均不在取值范围之内；好田灌域的长度比偏大，义勒力特灌域的长度比偏小；义勒力特灌域的分维值不符合Horton河系定律的合理取值范围，这说明察尔森灌区在渠道修建过程中，其现有大部分渠系的自组织优化结构受到人为破坏，现有渠系的输配水有效性较差。

1) 察尔森灌区好田灌域的分维值虽然在Horton河系定律的一般范围之内，但其分枝比和长度比均较大，这说明好田灌域现有渠系级别少，越级取水现象严重，渠系结构简单，在下一步的渠系改造中可适当减小斗渠数目，降低总干渠长度，增加渠系级别，如增加一级支渠以使其分枝比、长度比及分维值均在合理范围之内。

2) 义勒力特灌域的分枝比处于合理范围的下限，长度比偏小，而其分维数较大，这反映了该灌域支渠的数目少，在下一步渠系改造中，应适当增加支渠数目，减少斗渠与干渠长度，适当增加总干渠长度，以增加长度比为主，提高渠系输水效果。

3) 乌兰哈达及国光灌域的分枝比、长度比及分维值均在合理取值范围之内，这说明该灌域现有渠系分布结构符合水系自组织优化结构，在下一步渠系改造中，乌兰哈达灌域应重点从提高干渠及支渠的衬砌率入手，国光灌域应重点从提高干渠及斗渠的衬砌率入手。

4) 斯力很和哈达那拉灌域长度比和分维值均在合理取值范围之内，但其分枝比偏低，主要原因是这两个灌域支渠数量少，每个灌域仅有一条支渠，而斗渠数量多，配水效率低，今后可适当减少斗渠数量与长度，增加支渠数量及长度，以提高其分枝比，从而提高该灌域渠系的输配水效率。

4.2 分维数与渠系水利用效率关系分析

通过对察尔森灌区各灌域不同级别类渠系的渠系水利用效率与分维数进行相关性分析，作散点图1，以分析其总体趋势性变化规律。

从图1中各灌域渠系水利用效率与分维值关系可看出，各灌域渠系水利用效率与分维数之间基本呈大开口抛物线(R2=0.5499)，随分维数(D)增大，渠系水利用效率先减小后增大，拐点为(2.67,0.5912)，其所对应的分维值D已超过Horton河系定律所规定范围，因此通过增加分维数D,实现提高各灌域的渠系水利用效率不可取；察尔森灌区除义勒力特灌域外其它各灌域的分维值均小于2.67，且在Horton河系定律范围之内，上述各灌域可通过适当降低分维值以提高渠系水利用效率，从上述各灌域渠系特征参数计算结果可看出，察尔森灌区各灌域(除好田灌域)的分枝比小，不适宜再减小，而长度比接近取值范围下限，因此，可从增加各灌域(除好田灌域)的长度比，即适当增加上一级灌区渠系的长度，或相对缩短下一级渠系的长度，来提高渠系水利用效率。通过对察尔森灌区各灌域现有渠系分布形态分析，可知各灌域支渠数目少，因此可采取适当减少斗渠长度同时增加支渠数目与长度的方法降低分维数是察尔森灌区未来提高渠系水利用效率的方向之一。

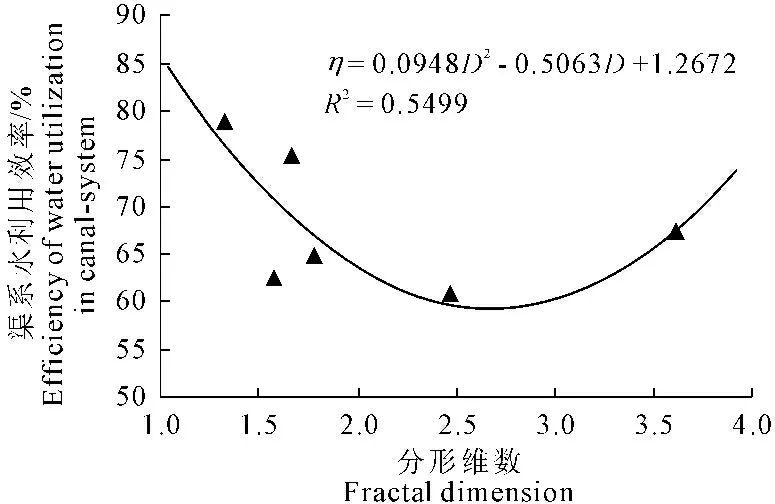
图1 分形维数与渠系水利用效率关系

Fig.1 The relationship between fractal dimension and efficiency of water utilization in canal-system

5 结 论

1) 察尔森灌区各灌域(除义勒力特灌域外)的分形维数虽然符合Horton河系定律，但大部分灌域的分枝比不在合理取值范围之内，表明现有大部分渠系的布置结构不符合自组织优化结构，渠系的级别设置及不同级别渠道的数量分配有待于进一步调整。

2) 在今后渠系节水改造中，根据上述分析所得分维数的相对合理取值，从优化渠系布置结构角度应适当降低斗渠长度，增加支渠数量与长度。

3) 渠系水利用效率影响因素作用机理比较复杂，本文仅从灌区渠系分形结构特征对渠系水利用效率的影响进行了分析，今后需要结合其它主要影响因素进行更深入研究，寻求各影响因素对渠系水利用效率的贡献率，以便为灌区渠系改造提供合理的指导，发挥渠系系统灌溉输配水的最大功效。

[1] 李建宏.干渠渠段输水损失测算分析[J].宁夏农学院学报，2002，(4):50-52.

[2] 任 可,王红雨.灌区输水渠道渗漏损失测算与分析[J].中国农村水利水电，2006，(12):16-20.

[3] 刘 战.灌溉水利用系数的影响因素及提高措施[J].陕西水利，2009，(4):136-139.

[4] James W Kirchner. Statistical inevitability of horton's lawsand the apparent randomness of stream channel networks[J]. Geology， 1993，21(7):591-594.

[5] 杨太华，苏维硫，何凡锋.黔南曹渡河流域水系的分形分维研究[J].贵州科学，1992，10(1)：60-66.

[6] 张宏才.水系分形研究的若干思考[J].咸阳师范学院学报，2003，18(6)：41-43.

[7] 陈彦光，李宝林.吉林省水系构成的分形研究[J].地球科学进展，2003，18(2)：178-184.

[8] 王卫红，徐 鹏，田世民.分形理论在河型研究中的应用探讨[J].泥沙研究，2010，(2)：35-41.

[9] 杨秀春，朱晓华.中国七大流域水系与洪涝的分维及其关系研究[J].灾害学，2002，17(3)：9-13.

[10] 贺军奇,吴普特,汪有科，等.渠道密度与渠系水利用系数关系研究[J].中国农村水利水电，2007，(2):17-18.

[11] 王小军，张 强，古璇清.基于分形理论的灌溉水有效利用系数空间尺度变异[J].地理学报，2012，67(9):1201-1212.

[12] 王小军,张 强,易小兵，等.灌区渠系特征与灌溉水利用系数的Horton分维[J].地理研究，2014，33(4)：789-800.

[13] 刘丙军，邵东国，沈新平.灌区灌溉渠系分形特征研究[J].农业工程学报，2005，21(12)：56-59.

[14] 屈忠义,杨 晓,黄永江,等.基于Horton分形的河套灌区渠系水利用效率分析[J].农业工程学报，2015，31(13):120-127.

[15] Turcotte D L. Fractals and Chaos in Geology and Geophysics[M]. Cambridge: Cambridge University Press， 1992.

[16] Batty M. Physical phenomena[J]. Geographical Magazine，1992,(7):35-36.

[17] La Barbera P, Rosso R. On the fractal dimension of stream networks[J]. Water Resources Research，1989，25(4):735-741.

[18] Schuller D J, Rao A P. Fractal characteristics of dense stream networks[J]. Journal of Hydrology，2001，243:1-16.

[19] 谢先红，崔远来，蔡学良.灌区塘堰分布分形描述[J].水科学进展，2007，18(6)：858-863.

[21] 龙腾文，赵景波.基于DEM的黄土高原典型流域水系分形特征研究[J].地球与环境，2008，36(4)：304-307.

Analysis on water utilization efficiency of canal-system on fractal theory in Chaersen irrigation district based

HUANG Yong-jiang1, QU Zhong-yi1, SHAO Zhong-ji2

(1.InstituteofWaterConservancyandCivilEngineering,InnerMongoliaAgriculturalUniversity,Hohhot,InnerMongolia010018,China；2.ChaersenIrrigationDistrictManagementBureauofInnerMongolia,Wulanhaote，InnerMongolia137400,China)

In order to provide a guidance for the canal water saving transformation and irrigation management, the relationship between the canal-system framework and the efficiency of water utilization in canal-system in Chaersen irrigation district were explored by using the fractal theory. The fractal dimension of the irrigation regions in Chaersen irrigation district (1.3 for Haotian, 3.6 for Yilelite, 2.5 for Wulanhada, 1.6 for Silihen, 1.7 for Guoguang, 1.8 for Hadanala) was calculated by the Horton River's law with the observation data on the irrigation canal system. The fractal dimension, combined with the actual measured data in 2013—2014, was used in analyzing the relationship between the fractal dimension and the efficiency of water utilization in canal-system. The results indicated that the efficiency of water utilization in canal-system and the fractal dimension of the irrigation regions showed a large opening parabola, the efficiency of water utilization in canal-system decreasing first and then increasing with the increase of the fractal dimension (D). The efficiency of water utilization in canal-system could be improved by properly reducing the fractal dimension in Chaersen irrigation district. To decrease the lateral channel length and increase the branch number and length was one way to improve the efficiency of water utilization in canal-system in Chaersen irrigation district in the future.

chaersen irrigation district; horton river's law; efficiency of water utilization in canal-system; fractal dimension

1000-7601(2017)02-0187-04

10.7606/j.issn.1000-7601.2017.02.30

2015-12-27基金项目：内蒙古水利厅专项(nmsl2013-1)

黄永江(1976—)，男，讲师，在读博士，主要从事节水理论与新技术研究。 E-mail：yongjianghuang168@126.com。

S274.4

A