基于MACRO的非圆二次旋转曲线轮廓的数控加工研究*
李润,邓龙
(兰州石化职业技术学院机械工程系,甘肃 兰州730060)
1 引言
随着数控技术的不断进步,数控车床加工各类复杂形面日渐增多。在数控加工过程中,我们比较习惯使用ISO代码指令编程,这些代码的功能是固定的,由数控系统厂家开发,使用者只需要按规定编程即可解决加工问题。但是很多零件的轮廓上含有椭圆、双曲线、抛物线等的二次非圆曲线,采用ISO代码编程就有一定的难度。手工编程对于这类零件的加工数学处理的任务是用直线段或圆弧段去逼近非圆曲线轮廓,需要计算少则几十个点,多则上万个点的坐标,存在处理周期长、计算工作量大、精度差、容易出错的缺点。如果使用CAD/CAM软件自动编程,虽然可以加工,但数控程序冗长,占用内存空间大,且无法应用于相似零件的加工。本文针对典型的非圆二次函数公式曲线轮廓零件的数控车床加工,阐述采用宏程序编程该类零件的过程与方法,实现普通编程难以实现的功能,扩大了数控车床的功能与加工范围[1]。
2 非圆旋转曲线宏程序编程
编制华中世纪星数控车床加工带有非圆旋转曲线轮廓类零件(如图1(a)、图1(b)所示)的宏程序,其中实半轴为a,虚半轴为b。

图1 非圆曲线零件加工图(椭圆:a=15、b=10)
2.1 工艺分析
车削非圆旋转曲线轮廓的回转零件时,通常先把工件坐标系原点偏置到该曲线对称中心上,然后采用直线逼近(也叫拟合)法,即在z向(或x向)分段,以 0.1~0.5 mm为一个步距,并把 z(或 x)作为自变量,x(或 z)作为 z(或 x)的函数[2,3]。
2.2 流程分析
(1)对曲线方程(参数方程)进行转化:根据轮廓曲线的解析几何方程式 y=f(x),将数学坐标转化为工件坐标,曲线方程中的坐标是数学坐标,要应用到数控车床上,必须要转化到工件坐标系中。
(2)求值公式推导:利用转化后的公式推导出坐标计算公式,建立数学模型。
(3)选定自变量并确定变量范围,非圆曲线中的x、z坐标或角度β均可以被定义为自变量,自变量确定后就可以确定因变量,并写出表达式。
(4)语句判断是否加工完毕,若未完毕,则返回继续执行加工程序,若是,则程序结束,其流程图如图2 所示[4,5]。

图2 非圆曲线通用宏程序开发流程
2.3 数学模型分析
2.3.1 非圆曲线数学模型分析
对于形如Ax2+Cy2+Dx+Ey+F=0非圆二次曲线一般方程,由二次项前系数的取值可以分为以下三种情况:
(1)若 A、C同号,且经配方后,等式等号右端为正数,方程表示椭圆;
(2)若 A、C 异号,经配方后,1)A>0 且等号右端为正数,方程表示焦点在平行于x轴直线上的双曲线;2)A>0且等号右式为负数,方程表示焦点在平行于y轴直线上的双曲线;
(3)若A、C中有一个为零,另一个不为零,则方程表示抛物线。
无论什么样的曲线,都可以看作是标准曲线经过平移或旋转或二者组合的结果,所以要加工一般曲线,可以从标准曲线入手,经过上述变换最后得到。
下面以图1(a)的加工曲线为例,来推导通用非圆二次旋转曲线的宏程序模块。分析比较图1(a)和图3不难发现,图3所示的轮廓 3就是图1(a)所示的加工轮廓曲线。轮廓1根据标准双曲线图4可知,其曲线方程为x2/a2-z2/b2=1,将其转换在直角坐标下的参数方程式为[6]:
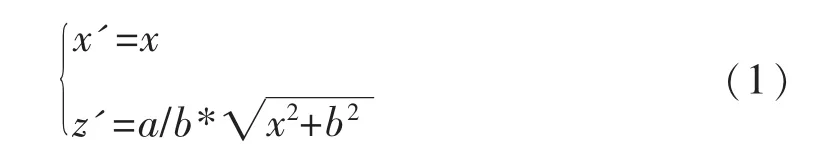
同理,可得到标准椭圆曲线的参数方程x2/a2+z2/b2=1,

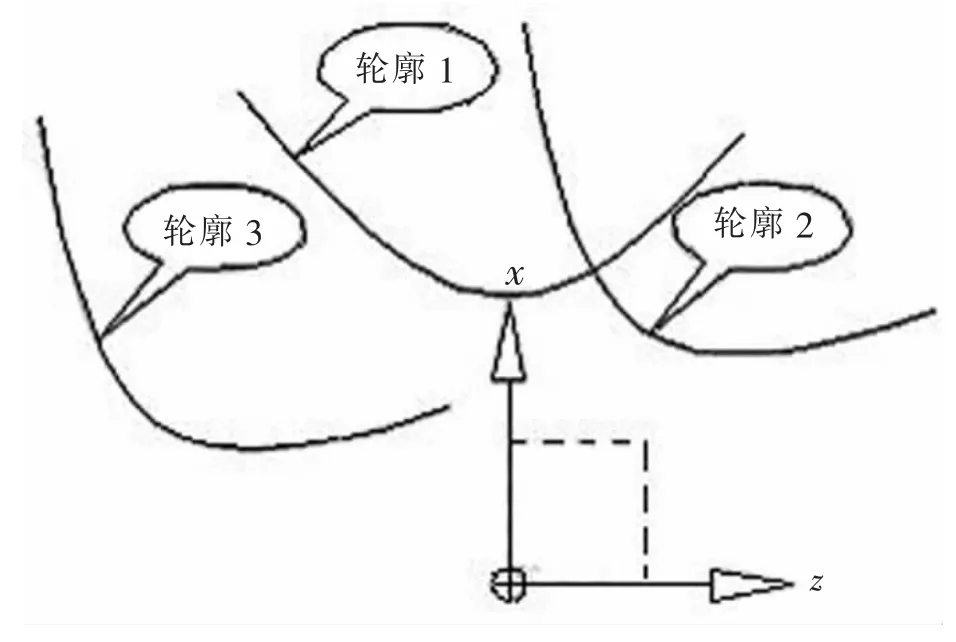
图3 旋转平移变换过程图

图4 上下对称的标准双曲线
2.3.2 图形绘制
以双曲线为例,借助CAD绘图软件Solidworks软件进行绘图。该软件设有表达式模块,可参数化设计,该软件结合Excel配置表,充分利用表格强大的公式计算、直观的参数输入、方便的数据维护功能,对模型参数进行驱动[7]。x作为变量(即表1中的U)从12到-14变化。
2.3.3 模型旋转变换
如图3所示,轮廓1要变为轮廓2需要绕原点逆时针旋转-30度,即θ=-30度。旋转变换方程为:

拆分出来即:

其中z1,x1是变换后的坐标值。
2.3.4 模型平移变换
如图3所示,轮廓1经旋转后,还要进行两个方向的平移,才得到轮廓3。由图3可知z方向平移-25,x方向平移-5。方程式变过程如表3所示。
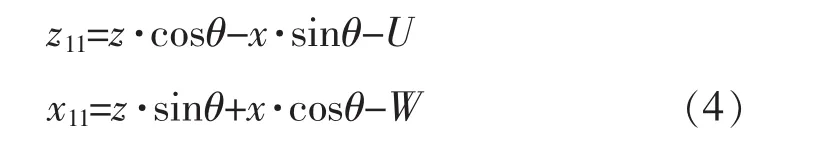

表1 旋转平移曲线绘制表
利用Solidworks软件中的表达式模块,应用规律曲线命令绘制图形。令x作为变量(即表1中的U)从12到-14变化。在excel工作表中输入表1所示的数据即得到图3所示经旋转又平移后的双曲线轮廓3。
运用上述同样的方法,可以得到其他非圆旋转平移曲线的加工轮廓。
3 非圆旋转曲线程序编制
变量定义见表2。

表2 变量定义表
通过上述分析,根据表达式(1)~(4)就能方便地编出如下旋转曲线的宏程序模块,定义一个变量#100。


4 实例分析
4.1 旋转双曲线、椭圆加工实例
加工如图1(a)、图1(b)所示零件,选用毛坯直径50 mm、长60 mm的铝合金为材料,左端三爪卡盘夹住,用90°外圆车刀(副偏角要稍大一些)粗精车,加工程序如下:


5 结束语
除了旋转双曲线和椭圆外,其他非圆曲线如抛物线、正弦曲线、余弦曲线、正切曲线、螺旋线等,都可以用类似的方法进行数学建模,然后用宏程序编程加工,解决了G代码指令所不能车削的特殊轮廓工件的加工难题。对于二次函数的非圆曲线轮廓,宏程序较之由CAD/CAM软件生成的程序插补精度高,程序短小精悍、运行速度快、加工效率高,宏程序在实际生产中有广泛的应用价值。
参考文献:
[1]陈海舟.数控铣削加工宏程序及应用实例[M].北京:机械工业出版社,2016.
[2]耿国卿,刘永海.数控车床编程与应用[M].北京:化学工业出版社,2017.
[3]冯志刚.数控宏程序编程方法、技巧与实例[M].北京:机械工业出版社,2016.
[4]李锋,白一凡.数控铣削变量编程实例教程[M].北京:化学工业出版社,2017.
[5]申小龙.数控加工技术[M].北京:冶金工业出版社,2015.
[6]林岩.数控车工技能实训[M].北京:化学工业出版社,2015.
[7]数控加工技师手册编委会.数控加工技师手册[M].北京:机械工业出版社,2016.

中国名胜 甘肃·宕昌 官鹅沟

