微机电系统姿态估计系统算法与仿真

魏振楠， 伊国兴， 徐泽远

(哈尔滨工业大学 航天学院，黑龙江 哈尔滨 150001)

微机电系统姿态估计系统算法与仿真

魏振楠， 伊国兴， 徐泽远

(哈尔滨工业大学 航天学院，黑龙江 哈尔滨 150001)

结合陀螺仪、加速度计误差模型，实现了以微机电系统(MEMS)陀螺仪与MEMS加速度计为基础的姿态估计硬件仿真系统，可用于模拟任意噪声强度和安装偏差下三轴捷联惯导系统(INS)，即按照给定运动曲线仿真输出陀螺仪与加速度计数据，为设计姿态估计算法提供仿真验证平台。同时，以姿态四元数为状态变量，载体俯仰角与横滚角为观测值设计了基于扩展卡尔曼滤波器(EKF)的姿态估计算法，俯仰角估计误差小于0.04°，横滚角估计误差小于0.05°，偏航角漂移速度0.01(°)/s。

姿态估计； 微机电系统(MEMS)惯导系统； 误差模型； 卡尔曼滤波

0 引 言

微机电系统(MEMS)姿态估计系统是指以微机械陀螺仪和加速度计等低成本惯性器件为敏感元件，利用捷联惯导算法并结合适当的数据融合手段，估计并输出载体三轴姿态信息的导航系统。由于微机械惯性器件成本低、体积小，由其构成的姿态估计系统在机器人姿态控制[1]、飞行器控制[2～4]、海洋卫星跟踪天线[5]、姿态测量[6]等领域越来越多的领域得到了应用。但微机械惯性器件噪声大、温漂剧烈等[7]问题也严重影响了姿态估计系统的精度，因而，在实现微机械导航系统时，设计稳定且快速收敛的滤波算法尤为重要。

本文以微机械陀螺仪与微机械加速度计输出模型为基础，实现了根据给定的运动曲线，设定参数输出陀螺仪与加速度计数据的微机械姿态估计硬件仿真系统，该系统为设计和验证导航算法提供仿真平台。同时，也提供了利用扩展卡尔曼滤波算法实现的姿态估计方法，用于验证仿真系统性能。

1 微机械惯性导航系统模型建立

本文以捷联形式建立微机械惯性导航系统(INS)仿真模型。

1.1 系统温度模型

系统温度模型包含理论温度变化模型和温度采样模型。理论温度变化模型描述系统核心器件温度随时间变化的规律，该模型利用数据表形式实现，给定系统特定时刻的温度，任意时刻的温度值利用牛顿插值获得。温度采样模型描述了包含采样噪声与温度传感器参数漂移所引起误差的系统核心器件温度测量值随时间变化的规律，设tk时刻系统理论温度值为T(tk)，参数漂移导致的随机游走误差为Twn(tk)，采样噪声误差为Trn(tk)，则系统温度采样模型输出为

Ts(tk)=T(tk)+Twn(tk)+Trn(tk)

(1)

1.2 系统运动模型

系统运动模型包含角运动模型与线运动模型。角运动模型描述了姿态角、姿态角速度以及姿态角加速度随时间变化的规律。线运动模型描述了载体位移、速度及加速度随时间变化的规律。系统运动模型利用数据表实现，根据需求产生指定采样周期的离散角运动与线运动轨迹后，任意时刻运动参数通过牛顿插值获得。

1.3 微机械陀螺仪系统模型

捷联惯导系统中，陀螺仪实际输出与载体运动角速度不完全一致，其受陀螺安装偏差、漂移、刻度系数误差等因素影响。

陀螺安装偏差指陀螺仪敏感轴与相应载体坐标轴不重合，使得该方向陀螺仪不仅仅敏感自身方向角速度，还受其它轴角速度的耦合影响，由陀螺安装偏差导致的角速度测量误差可通过对陀螺仪安装角进行标定补偿。设i方向陀螺与j方向载体坐标轴夹角为ψij，则捷联惯导系统中三轴陀螺仪安装矩阵可表示为

(2)

陀螺仪漂移及刻度系数误差为随机误差，刻度系数误差Sg一般使用随机常数描述，漂移则可分为逐次启动漂移(常值零偏)、慢变漂移(随机游走)、及快变漂移(白噪声)等[8]，则捷联惯导系统中三轴陀螺仪输出模型可表示为

ωgo=diag(1+sgx,1+sgy,1+sgz)Mgωgv+ωgb+ωgr+ωgn

(3)

式中ωgo为陀螺仪输出;sgi为i轴方向陀螺仪标度系数误差;ωgv为载体角速度输入;ωgb为陀螺仪逐次启动漂移;ωgr为慢变漂移，ωgn为快变漂移。

考虑到陀螺仪饱和特性及温度特性，最终陀螺仪仿真模型如图1所示。

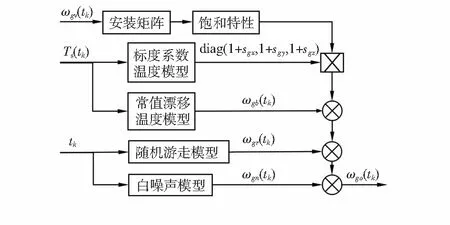
图1 陀螺仪仿真模型

1.4 微机械加速度计系统模型

同陀螺仪一样，捷联惯导系统中加速度计的输出亦受安装偏差，漂移及标度系数误差等影响；与陀螺仪不同的是，在导航系统中使用加速度计进行姿态角测量时，慢变漂移对于角度测量精度影响不大，故为了降低滤波器维度，一般仅考虑逐次启动漂移fab及快变漂移fan。

设i方向加速度计与j方向载体坐标轴夹角为Γij，则捷联惯导系统中三轴陀螺仪安装矩阵可表示为

(4)

则系统中三轴加速度计输出模型可表示为

fao=diag(1+sax,1+say,1+saz)Mafav+fab+fan

(5)

式中fao为加速度计输出;fav为载体加速度输入;fab为加速度计逐次启动漂移;fan为加速度计快变漂移。

考虑到加速度计饱和特性及温度特性，最终加速度计仿真模型如图2所示。

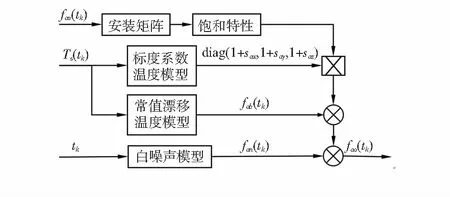
图2 加速度计仿真模型

2 姿态估计系统算法

姿态用于表征坐标系与坐标系间的相对旋转关系，载体坐标系与导航坐标系间姿态角常用方位角β、俯仰角α以及滚动角γ表示。

2.1 坐标系定义与变换关系

系统中主要应用载体坐标系O-xyz与导航坐标系O-ENU，姿态角定义如图3所示。O-xyz坐标轴选取遵循“右前上”原则，与载体固联；O-ENU坐标轴选取遵循“东北天”原则，随载体运动在地球表面平移和旋转。

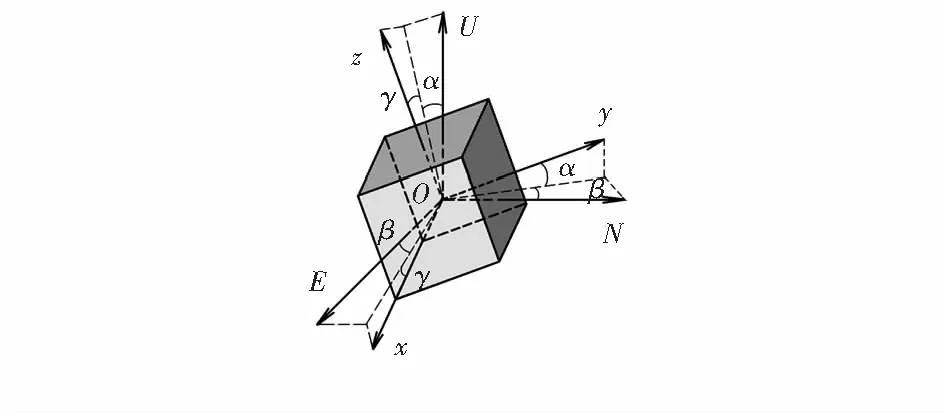
图3 姿态角定义

载体坐标系到导航坐标系姿态变换矩阵为

(6)

采用四元数Q=[q1q2q3q4]T表示为[9]

(7)

则采用载体四元数可计算得到载体姿态角

(8)

2.2 扩展卡尔曼滤波算法

在此使用扩展卡尔曼(EKF)，解决由于利用加速度计解算姿态角时存在三角函数运算而导致的观测方程非线性问题。

选取四元数Q作为系统状态变量，则系统状态预测方程为

Q(k)=A(k)Q(k-1)

(9)

其中状态转移矩阵

A(k)=

选取俯仰角及横滚角为观测变量，即z=[αγ]T。由于式(8)具有非线性，现对其进行线性化处理。记F(q1,q2,q3,q4)=[α(q1,q2,q3,q4)γ(q1,q2,q3,q4)]T，其雅各比矩阵为

(10)

其中

(11)

设重力加速度在导航坐标系O-ENU中投影为G=[0 0g]T，其在载体坐标系O-xyz中投影为Xg=[xgygzg]T，则可得俯仰角α与横滚角γ计算公式

(12)

综上,得到以Q为状态变量，以α,γ为观测值的扩展卡尔曼姿态角估计算法，时间更新方程如式(13)所示，状态更新方程如式(14)所示

(13)

(14)

3 微机械姿态估计系统仿真实验

现以俯仰轴为例分析仿真结果。

3.1 微机械系统仿真标定

对比表1、表3，可以看出：对于标度系数，陀螺仪与加速度计的标定分辨率为0.000 1，由于考虑了陀螺仪的随机游走噪声，其零偏标定分辨率仅为0.1，而未考虑随机游走噪声的加速度计，其零偏标定分辨率可达到0.000 1。对比表2、表4，可知系统中陀螺仪与加速度计的敏感轴安装角标定精度均能达到0.01°。在给定角运动曲线情况下，陀螺仪原始输出、经补偿输出以及角速度测量误差如图4所示;加速度计原始输出、经补偿输出及加速度测量误差如图5所示。可以看出：由于标度系数误差、零漂、安装偏差角等存在，陀螺仪与加速度计测量结果与真实值存在偏差，经过标定补偿后，偏差明显减小，剩余偏差统计特性与设定的陀螺仪与加速度计模型中测量白噪声统计特性相当。

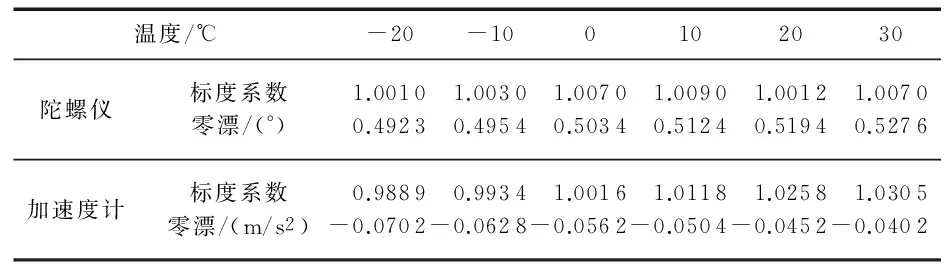
表1 陀螺仪、加速度计标定系数及零偏温度模型

表2 陀螺仪、加速度计安装角度

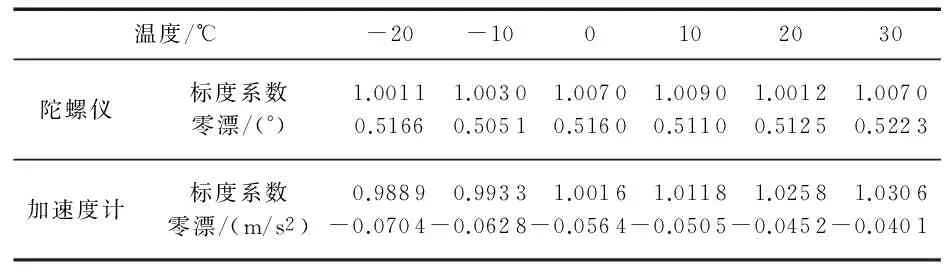
表3 陀螺仪、加速度计标定系数及零偏温度标定模型

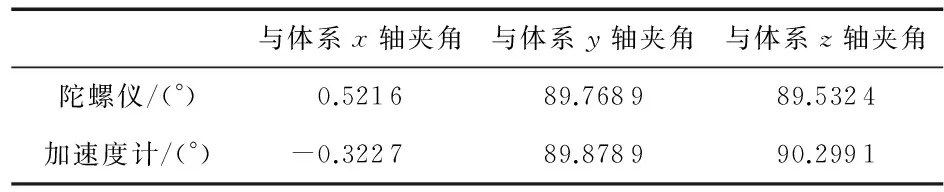
表4 陀螺仪、加速度计安装角度标定结果

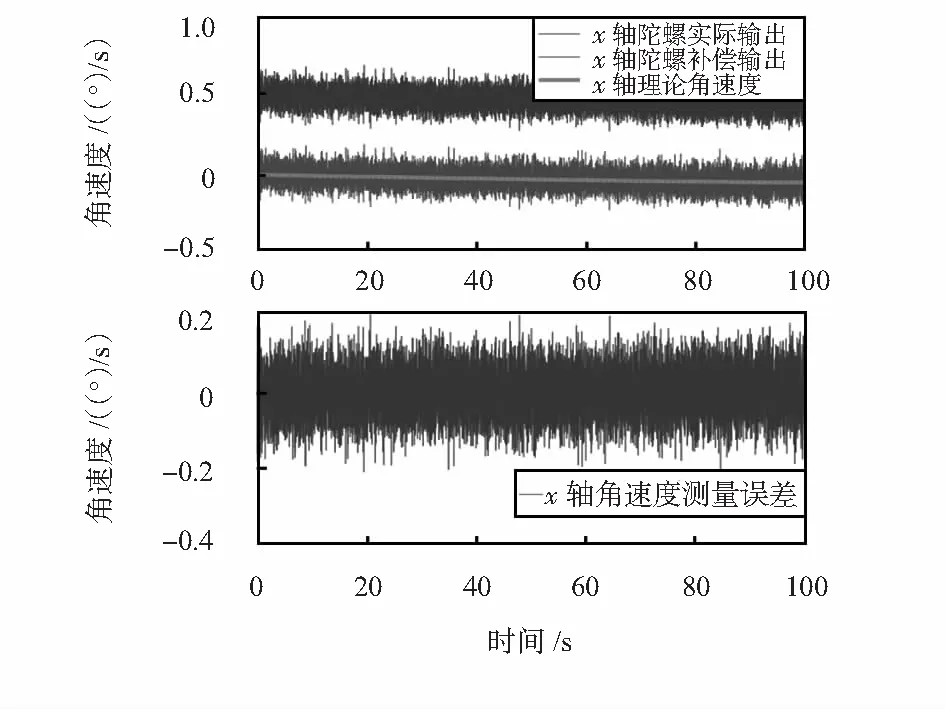
图4 陀螺仪原始输出、其经过补偿后的输出以及角速度测量误差

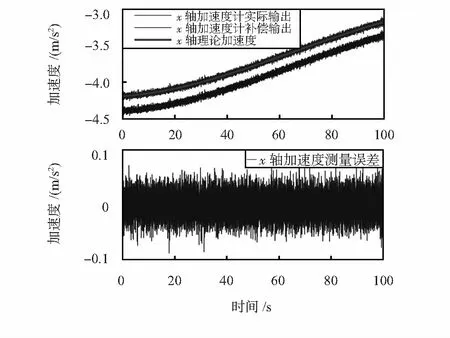
图5 加速度计原始输出、其经过补偿后的输出及加速度测量误差

3.2 姿态估计系统仿真测试

由图6可知，利用加速度估计载体姿态角其均值与理论值吻合，但单次测量偏差较大，其角度测量标准差约为0.1°；由图7可知，利用陀螺仪积分估计载体姿态角，其估计值变化平稳，但由于陀螺仪存在随机漂移，其零偏无法完全补偿，姿态角估计结果会随时间发散；由图8可知，利用EKF算法，融合加速度计与陀螺仪测量结果，既减小了单次角度估计误差，又很好地抑制了角度估值的漂移，俯仰角估计值误差小于0.05°。

图6 载体俯仰角理论值、加速度计估计值以及估计误差

图7 载体俯仰角理论值、陀螺仪积分估计值以及估计误差

图8 载体俯仰角理论值、EKF估计值及估计误差

实际上，由于采用加速度计仅能观测载体的俯仰角与横滚角，故而该滤波器对于载体方位角发散无任何抑制作用，如图9所示。

图9 载体方位角EKF估值与理论值

4 结 论

本文详细分析了INS中陀螺仪与加速度计输出模型，在考虑到系统温度模型、传感器标度系数温度模型与零偏模型、传感器饱和特性等客观条件前提下，实现了微机械姿态估计硬件仿真系统，配合适当载体角运动与线运动模型，可输出指定参数下的陀螺仪与加速度计数据，为设计和验证导航算法提供仿真平台。此外，本文提出了一种应用EKF算法进行加速度计与陀螺仪数据融合估计载体姿态角的方法，通过仿真验证，该算法俯仰角估计误差小于0.04°，横滚角估计误差小于0.05°，偏航角漂移速度约0.01(°)/s。

[1] Hu Y,Yan Y,Liang J,et al.A miniature,low-cost MEMS AHRS with application to posture control of robotic fish[C]∥2013 IEEE International Instrumentation and Measurement Technology Conference(I2MTC),IEEE,2013:1392-1395.

[2] Safaee A,Moussavi S Z,Mehrabani M S,et al.Construction and control of monocopter using MEMS AHRS[C]∥11th IEEE International Conference on Control & Automation(ICCA),IEEE,2014:219-224.

[3] 刘辉邦,褚金奎,支 炜,等.基于STM32的无人机姿态测量系统设计[J].传感器与微系统,2013,32(8):108-110.

[4] 胡少兴,刘东昌,张爱武,等.一种基于MEMS传感器的无人飞艇航姿测量系统[J].传感器与微系统,2014,33(3):58-61.

[5]WangY,HussainA,SoltaniM.AMEMS-basedadaptiveAHRSformarinesatellitetrackingantenna[J].IFAC-PapersOnline,2015,48(16):121-126.

[6] 黄 旭,王常虹.基于微机械惯性器件和磁强计的姿态航向系统[J].传感器与微系统,2005,24(8):54-56.

[7]DuJ,GerdtmanC,LindenM.SignalprocessingalgorithmsfortemperauturedriftinaMEMS-gyro-basedheadmouse[C]∥2014InternationalConferenceonSystems,SignalsandImageProces-sing,IEEE,2014:123-126.

[8] 秦永元,张洪钺,汪叔华.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社，2015:332-335.

Algorithm and simulation of MEMS attitude estimation system

WEI Zhen-nan, YI Guo-xing, XU Ze-yuan

(School of Astronautics,Harbin Institute of Technology,Harbin 150001,China)

An attitude estimation hardware simulation system is realized by using MEMS gyroscopes and MEMS accelerometers,which is based on error model of gyroscope and accelerometer.The system can be used to simulate three-axis strapdown inertial navigation system(INS)under the situation of any noise intensity and installation error,that is to output data of gyroscopes and accelerometers according to given motion curve,in order to supply simulation verification platform for designing attitude estimation algorithm.Meanwhile,an attitude estimation algorithm which is based on extended Kalman filter is designed.In the algorithm,the attitude quaternion is chosen as state variable,the pitching angle and roll angle are chosen as observed variables.As a result,estimation error of pitching angle is less than 0.04°,estimation error of roll angle is less than 0.05°,and the drift rate of yaw angle is 0.01(°)/s.

attitude estimation; MEMS INS; error model; Kalman filtering

10.13873/J.1000—9787(2017)05—0149—04

2016—05—22

V 249

A

1000—9787(2017)05—0149—04

魏振楠(1992-)，男，硕士研究生，主要研究方向为组合导航。