大气介质环境后向散射穆勒矩阵的特性分析*

郑骊昂， 高 隽， 于 洋， 范之国

(合肥工业大学 计算机与信息学院，安徽 合肥 230009)

大气介质环境后向散射穆勒矩阵的特性分析*

郑骊昂， 高 隽， 于 洋， 范之国

(合肥工业大学 计算机与信息学院，安徽 合肥 230009)

后向散射穆勒矩阵仿真应用的研究具有很多潜在的优势，通过分析穆勒矩阵元素传递的信息可以有效辨别介质特性。以大气环境介质为探究背景，通过偏振蒙特—卡洛仿真方法建模，分析了不同大气环境介质情形下，穆勒矩阵元素的变化规律。仿真结果表明：随介质粒子尺寸增加，穆勒矩阵元素整体呈现向中心收缩态势，特定元素对粒子尺寸敏感，其径向峰值可以明显反映粒子尺寸变化；随介质粒子浓度增加，穆勒矩阵元素强度衰减，特定元素圆周曲线幅值可以反映粒子浓度变化。

大气环境； 穆勒矩阵； 偏振特性； 蒙特—卡罗方法

0 引 言

偏振光在散射介质中传输的相互作用过程中，其携带的初始偏振状态会由于散射介质特性发生变化[1]，由此可以获得大气光学特性相关的偏振信息。通过研究散射光的偏振态变化推断散射介质性质的应用相当广泛，例如，工业上用于测量云、雨、雾的特性，天文上用于研究大气和宇宙尘埃等。然而，单方面探究偏振态变化，并不能够获取介质全面的光学特性。穆勒矩阵可以全面反映光学目标更多维的信息，因此，对介质目标穆勒矩阵的研究具有重要的意义。

在偏振光早期应用研究中，大多数学者使用特定偏振片实现偏振光入射，并用检偏器调制分析散射后的偏振光，通过不同的线偏光调制组合获得散射介质的相关信息。Hielscher A H[2，3]团队最先开展使用水平、垂直多组入射出射光路组合，研究生物细胞悬液等浑浊强散射介质的实验，证明了使用偏振散射光在识别生物细胞粒径、浓度、性质等方面存在潜在研究意义，随后首次将斯托克斯穆勒矩阵描述方法引入偏振光后向散射的实验研究，通过实验证明了穆勒矩阵中的特定元素对聚苯乙烯悬浮粒子半径敏感，同时可以区分癌细胞和非癌细胞。同时，很多学者开始使用数值解析模型方法描述偏振光在散射介质中的传输过程。Voshchinnikov N V和Karjukin V V[4]研究了光在星周尘中偏振辐射传输的蒙特卡罗模拟方法，Bartel S等人[5]结合单次Mie散射理论，将蒙特—卡洛方法与斯托克斯穆勒矩阵结合，探究了区分粒子尺寸和髙散射光学特性的方法，为穆勒矩阵在生物组织中的表征研究提供依据。由于大气环境介质影响因素较为复杂，之前学者大多使用数值模拟方法探究偏振光在生物组织中的传输，较少涉及其在大气环境背景下的应用探究，本文将针对大气环境，控制单一变量求解环境目标穆勒矩阵，将穆勒矩阵方法应用于研究不同大气环境介质的偏振特性。

本文采用了Matlab蒙特—卡罗仿真模型，建立了大气环境介质后向散射仿真平台，给出了大气环境目标下的穆勒矩阵求解方法，提出了使用穆勒矩阵元素及穆勒矩阵解偏特性分析介质粒子尺寸及浓度的方法，并求解得到其对应规律，为分析和探测大气介质环境特性提供了新的思路。

1 后向散射穆勒矩阵求解方法

偏振光的偏振状态通常使用斯托克斯矢量完整描述，该矢量包含4个分量即[IQUV]，当偏振光与目标介质相互作用时，其偏振状态会发生变化。通常把目标介质对入射光的作用等效为一个线性的变换矩阵，称为穆勒矩阵。当入射特定偏振态，其偏振状态的变化可以通过目标的穆勒矩阵表示

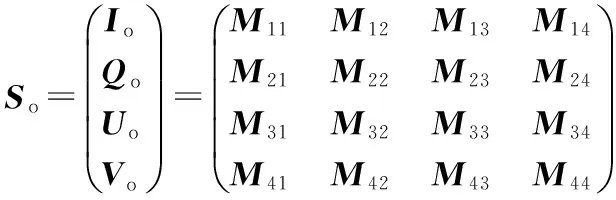
(1)

式中So为出射光斯托克斯矢量，Si为入射光斯托克斯矢量，M为散射介质或光学系统的穆勒矩阵，全面记录了介质或光学器件对入射偏振态的变换作用，反映的是介质的偏振光学特性，主要与介质的折射率、浓度以及散射单元本身的性质及分布有关，与入射偏振态无关。

本文研究目的是通过仿真得到不同情形下大气环境介质的后向散射穆勒矩阵，通过分析其穆勒矩阵元素，得到介质的信息。其中，后向散射穆勒矩阵是通过数值模拟方法计算得到[5]，首先设定光子的初始偏振态为4个正交向量

S1=[1 0 0 0]T，S2=[1 1 0 0]T

S3=[1 0 1 0]T,S4=[1 0 0 1]T

(2)

实际实验测量穆勒矩阵时，通常是调制入射光的偏振状态，得到多种偏振状态的入射光，让其经过介质散射，由CCD获取出射光的斯托克斯矢量光强分量，再通过多组代数运算得出穆勒矩阵。而仿真过程可以直接获得出射光完整的4个斯托克斯矢量元素，故穆勒矩阵通过联立4组方程即可直接计算求得

(m11,m12,m13,m14)T=M·S1=(M11,M21,M31,M41)T

(m21,m22,m23,m24)T=M·S2=

(M11+M12,M21+M22,M31+M32,M41+M42)T

(m31,m32,m33,m34)T=M·S3=

(M11+M13,M21+M23,M31+M33,M41+M43)T

(m41,m42,m43,m44)T=M·S4=

(M11+M14,M21+M24,M31+M34,M41+M44)T

(3)

在仿真中，当跟踪大量光子入射介质后，其后向散射接收得到的斯托克斯矢量便不再能够用单值描述，而是所有入射粒子与介质随机作用的叠加，因此，最终的斯托克斯矢量每个分量为二维图像，图像中每个像素点的强度值即为空间上单个粒子的斯托克斯矢量经过介质穆勒矩阵作用的信息累积，最终求解得到的穆勒矩阵16个元素即为16幅二维图像。

2 蒙特—卡罗多次散射建模

本文采用偏振蒙特—卡罗方法模拟光子在大气环境中的多次散射过程，主要通过计算机产生的伪随机数模拟一定数量的光子随机行走过程来实现光束散射传输的效果。偏振蒙特—卡罗方法由于计算方法简单、模拟精度高，在大气探测、海洋遥感及生物医学等方面有广泛应用[6,7]。该方法包括入射光源、接收平面以及散射介质3个基本要素，如图1所示。一束激光从空间垂直入射到半无限散射介质，在介质内部的随机位置处与粒子多次碰撞发生散射、吸收后，当光子被完全吸收或者沿接收平面的方向出射，认为单次散射仿真过程结束。

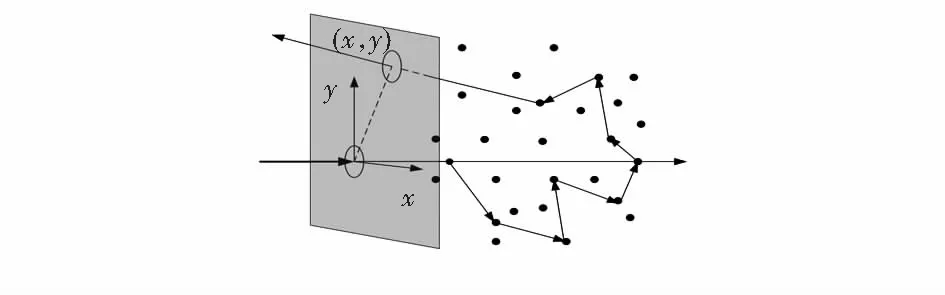
图1 蒙特—卡罗模型光子散射示意图

本文利用Matlab对光子在大气环境中的偏振传输过程进行建模仿真，偏振蒙特—卡罗方法的算法框图如图2所示，详细计算步骤可参考Jessica总结的偏振蒙特卡罗子午面模型[8]。

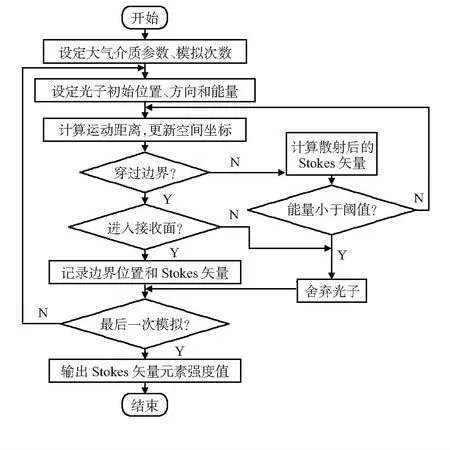
图2 蒙特—卡罗仿真算法流程

3 仿真实验与分析

针对前述穆勒矩阵测量机理的分析和基于蒙特—卡洛的多次散射建模方法，设计了两种仿真实验来分析不同大气环境下，后向散射穆勒矩阵的特性。无特殊说明，仿真过程的参数统一为：入射波长为580nm，光束从原点入射，后向散射接收面垂直接收光子，面积大小为100像素×100像素，模拟光子总数为106个。

3.1 不同半径大气环境粒子的仿真

为了研究大气介质粒子尺寸分布对于大气环境偏振特性的影响，实验中，选取大气成分中较多的气溶胶粒子作为仿真对象，设置粒子半径分别为0.6，2.0，6.0μm，各项异性因子为0.202，复折射率为m=1.53+0.008i[9]。图3展示了3种不同粒子半径大气环境介质的穆勒矩阵图样，各元素均以M11最大强度值进行归一化。通过观察可以发现，M12与M21,M13与M31,M23与M32呈现相同的花瓣分布，并沿矩阵斜对角线成对称分布，即Mnm=Mmn，且图案表现出很强的角度依赖性。同时，观察M22和M33，M21和M31可以发现，这几对只是在角度上呈45°旋转关系，光强没有太大差异。仿真结果与之前作者结论[3]吻合，证明了仿真结果的正确性。

图3 不同半径大气介质粒子穆勒矩阵图案

对于不同尺寸大气粒子，从穆勒矩阵图样可以捕捉到一定的规律。16个穆勒矩阵元素被称为介质的“指纹”，不同介质之间的差异必定能够通过矩阵中的特定元素呈现。对比3幅图案，M12，M13，M21，M31元素强度值呈现一定的衰减，当粒子半径较大时，其中心幅值接近于0。M22，M33，M44元素随着粒子半径增大，呈现明显的向中心收缩趋势。一般来说，大颗粒前向散射成分较大，小颗粒后向散射成分较大，当散射单元粒子半径逐渐增大，其后向散射的图样会呈现一种强度衰减的趋势。由于单幅图案都是以M11最大值归一化，故横向比较时，只探究元素图样上的花瓣强弱和径向伸缩，并不能得到关于大气介质的更多信息。下面选取不同大气介质尺寸下的M44元素进行分析。

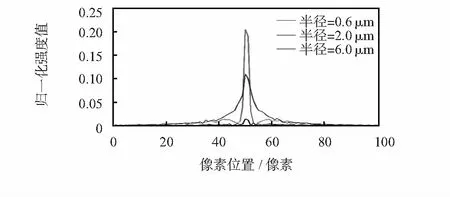
图4 不同半径大气介质粒子穆勒矩阵M44元素径向强度分布

图4中，选取上述3种不同粒子穆勒矩阵M44的强度值图案，沿矩阵元素中心线横轴展开得到。X轴为像素值，Y轴为各像素点对应光强值。从图中可以明显看出，元素中心区域接受到的光子辐射强度值最高，从中心向两边强度逐渐衰减，不同的粒子半径呈现不同的曲线走势，但由此可以得出，M44元素对粒子尺寸较为敏感，较小的粒径变化会呈现较大的振幅起伏，从而可以用于区分不同尺寸大气环境介质的特性。

3.2 不同浓度大气环境粒子的仿真

对于不同浓度条件的仿真，设置大气介质粒子半径为1.0 μm，介质浓度依次为10,20,30个/mm3[10]进行分组试验。根据Mie散射原理，浓度越大，则介质散射系数大，随机介质后向散射矩阵各元素的二维分布图样会减小。主要原因是入射光子发生散射的概率与介质的散射系数成正比，浓度越大，光子散射的概率越大，散射过程中偏振信息、光强信息丢失越多，所以，可探测到的光强越来越小，图案的角度依赖特性也越来越不明显。

为了更好地显示出穆勒矩阵图案的变化趋势和对称特性，图5将3种不同浓度下获得的穆勒矩阵中M21元素进行圆周展开分析，以入射点为圆心，一定长度为半径做圆，并规定垂直向上为0°起点，竖直向下为180°，圆周沿逆时针依次方向取像素值点，在直角坐标系上沿角度值展开。由可以看出，曲线振幅可以明显区分出介质浓度的不同，浓度

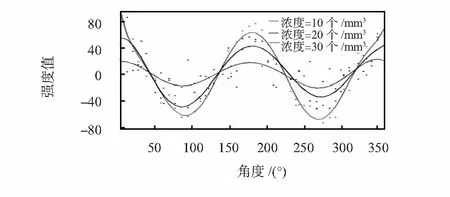
图5 不同浓度大气介质环境穆勒矩阵M21元素圆周展开图

越大的介质，经过散射后呈现振幅越小，从而可以辨别不同浓度的大气环境介质。

4 结束语

本文针对不同大气环境介质对后向散射光偏振特性的影响问题，基于典型蒙特—卡罗偏振散射模型，结合斯托克斯穆勒矩阵分析方法，从介质粒子浓度和尺寸两个方面进行仿真实验，分析得到大气环境介质偏振特性的结论：对于不同粒子尺寸的介质，随半径增加，其散射强度减小，穆勒矩阵元素的图样整体收缩，特定矩阵元素的径向峰值可以明显反映粒子尺寸变化；对于不同浓度介质，随浓度增加，特定矩阵元素圆周展开曲线幅值可以反映粒子浓度变化规律。因此，运用后向二维散射穆勒矩阵元素分析大气环境特性的方法是可行的，为开展实验研究提供了一定参考。

[1] Deschamps P Y,Bréon F M,Leroy M,et al.The POLDER mission: Instrument characteristics and scientific objectives[J].IEEE Transactions on Geoscience and Remote Sensing,1994,32(3):598-615.

[2] Hielscher A H,Mourant J R,Bigio I J.Influence of particle size and concentration on the diffuse backscattering of polarized light from tissue phantoms and biological cell suspensions[J].Applied Optics,1997,36(1):125-135.

[3] Hielscher A,Eick A,Mourant J,et al.Diffuse backscattering Mueller matrices of highly scattering media[J].Optics Express,1997,1(13):441-453.

[4] Voshchinnikov N V,Karjukin V V.Multiple scattering of pola-rized radiation in circumstellar dust shells[J].Astronomy and Astrophysics,1994,288:883-896.

[5] Bartel S,Hielscher A H.Monte Carlo simulations of the diffuse backscattering Mueller matrix for highly scattering media[J].Applied Optics,2000,39(10):1580-1588.

[6] 王子谦,张旭东,金海红,等.基于Monte Carlo方法的混浊大气偏振模式全天域建模[J].中国激光,2014(10):213-221.

[7] 林 勇,徐智勇,汪井源,等.雾环境下非视距大气散射传输特性研究[J].光学学报,2013(9):1-5.

[8] Ramella-Roman J,Prahl S,Jacques S.Three Monte Carlo programs of polarized light transport into scattering media:Part I[J].Optics Express,2005,13(12):4420-4438.

[9] 蔡 嘉,高 隽,范之国,等.湿度对气溶胶单粒子偏振特性的影响研究[J].传感器与微系统,2013,32(9):35-38.

[10] 刘瑞芳.人工雾的激光辐射特性分析及雾参数反演研究[D].南京：南京信息工程大学,2005.

郑骊昂(1990 -)，男，硕士研究生，研究方向为智能信息处理。

Characteristic analysis of backscattering Mueller matrix in atmosphere medium environment*

ZHENG Li-ang, GAO Jun, YU Yang, FAN Zhi-guo

(School of Computer and Information，Hefei University of Technology，Hefei 230009，China)

Backscattering Muller matrix simulation is widely used in many tasks.By analyzing information of Mueller matrix elements,atmospheric medium properties can be distinguished.To investigate atmospheric environment medium,use Monte Carlo modeling to simulate the variation rule of Mueller matrix with respect to different atmospheric medium.The simulation results show that,with the increasing of particle size,Mueller matrix elements come to the center.As Muller matrix elements are sensitive to particle size,radial peak of specific elements can clearly reflect the changes of particle size.With the increasing of medium particle concentration,elements intensity of Mueller matrix weakens,amplitude of specific elements can reflect the changes of particle concentration.

atmosphere medium environment; Mueller matrix; polarization property; Monte Carlo method

10.13873/J.1000—9787(2017)05—0022—03

2016—05—25

国家自然科学基金资助项目(61571175,61571177)

O 436

A

1000—9787(2017)05—0022—03