基于GB/T17855-1999方法的端面花键齿承载能力计算

唐波，陈世堂，吴国

（1.浙江运达风电股份有限公司 风力发电系统国家重点试验室，浙江 杭州 310012；2.上海振华重工（集团）股份有限公司，上海 200125）

基于GB/T17855-1999方法的端面花键齿承载能力计算

唐波1，陈世堂1，吴国2

（1.浙江运达风电股份有限公司 风力发电系统国家重点试验室，浙江 杭州 310012；2.上海振华重工（集团）股份有限公司，上海 200125）

通过将端面花键齿模型转换为圆柱外花键模型，分析端面花键齿转换过程，运用力学理论计算方法，比较端面花键与圆柱外花键齿的承载差异，沿用《GB/T 17855-1999花键承载能力计算方法》标准的思路，最终整理得到端面花键齿承载能力的计算方法。并以端面花键齿SWC780BF为例，采用通用算法和有限元直接计算方法与之计算结果进行比较验证，计算结果表明，两者的应力水平基本一致，采用该方法对端面花键齿进行计算可行。

端面花键齿；承载；强度；有限元；方法探究

1 研究背景及意义

近年来，伴随着船舶、航空等工业的飞速发展，花键联接作为一种常用联接型式，广泛应用于传动机构中。端面花键齿作为一种特殊的花键型式，已成为万向联轴器传动机构的常用联接型式之一。目前，仅在国内万向联轴器标准中，对端面花键齿的主要参数有相应描述，但对于如何进行端面花键齿承载能力计算以及如何进行强度等方面的衡准则尚不明确。这对于端面花键齿的系列化和非标设计方面，带来了诸多的不确定因素。

国内现行标准《GB/T 17855-1999花键承载能力计算方法》详细讲述了圆柱渐开线花键和圆柱矩形齿花键的承载能力计算的过程、衡准以及相应的实例，但对端面花键承载计算，如何进行转换应用以及如何衡准，则没有相应的描述。

本文以万向联轴器的端面花键齿SWC780BF为例，在标准《GB/T 17855-1999花键承载能力计算方法》的基础上进行了假定和理论延伸，对端面花键齿的承载能力进行了详细计算，并运用花键的通用算法和有限元直接计算方法进行了比较验证。

鉴于端面花键齿承载方向虽与圆柱花键不同，但在传递扭矩时各齿面力的传递则有很多相似之处，可以通过相应的假设转换，将端面花键齿模型转化成圆柱外花键模型，再沿用圆柱花键的计算方法对端面花键齿承载能力进行计算。模型转换及转换后的键齿啮合示意图详见图1、2所示。

本文参照参考文献[2]中重心位置简化处理方法，选取端面花键齿长度的中截面为计算截面，如图1中2R所示位置。

其中，Dee、 Die、D和Dii等相关参数的说明和转换公式详见表1。

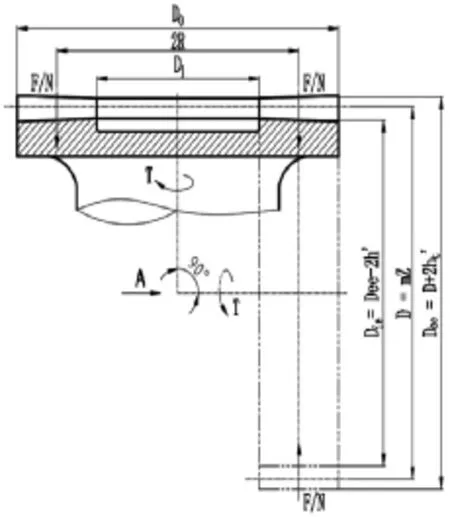
图1 端面花键齿计算模型转换

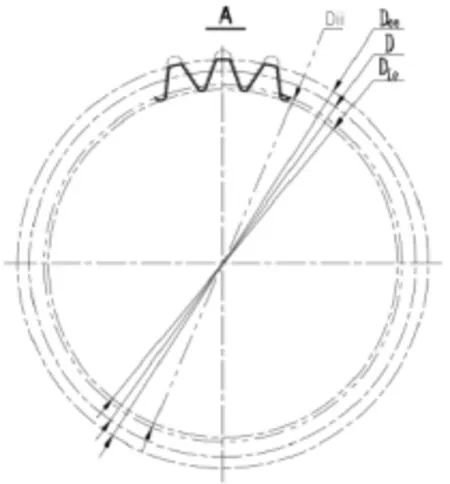
图2 转化后花键模型及键齿啮合示意

2 术语与代号

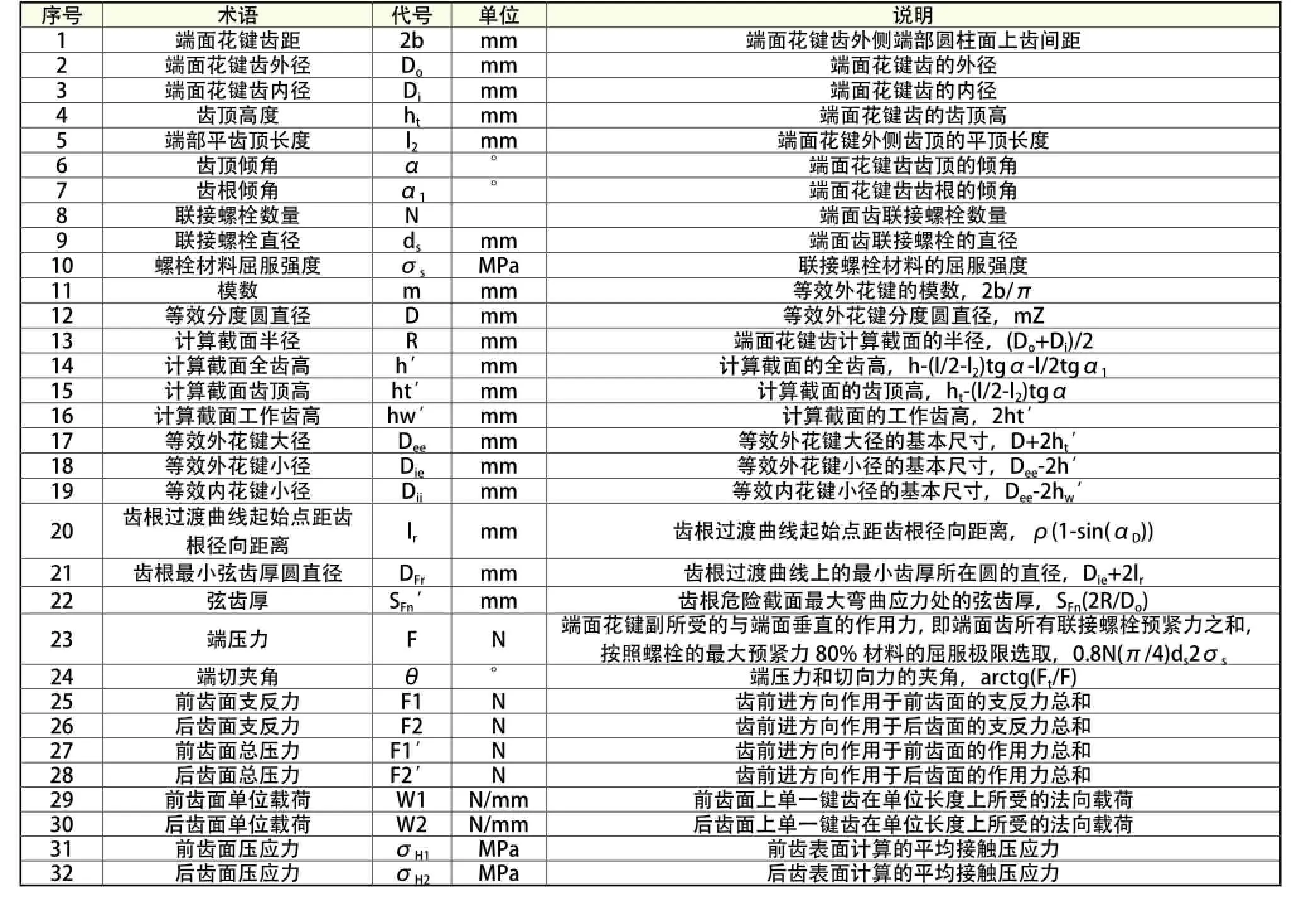
表1 术语、代号及说明

2.1 术语与代号说明

本文的术语定义与GB/T 17855-1999的术语定义基本一致，对于不同于圆柱外花键的部分术语，本文进行了整理并对术语定义和计算方法做了详细的说明，详见表1。其它未列出术语见GB/T 17855-1999标准中的表1的定义。

2.2 齿面主要术语

齿面主要术语，如图3所示。

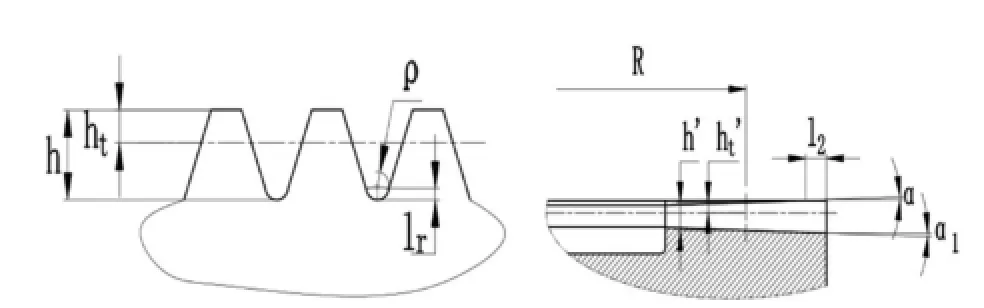
图3 齿面主要术语示意图

3 齿面受载分析和计算主要说明

端面花键齿通过联接螺栓预紧力将端面齿的齿面紧密的贴合在一起，通过齿面间的挤压作用来传递扭矩。如果将所有螺栓的预紧力和传递的转矩简化到其旋转中心位置，则可得知端面齿只承受转矩和端压力两种载荷作用，如图4所示。

图4 端面花键齿受载模型

将螺栓预紧力和传递的扭矩叠加后，沿端面花键齿计算截面（圆柱面）周向均匀展开，如图5所示。

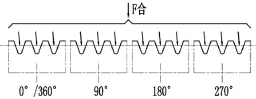
图5 端面花键齿载荷周向展开示意图

展开后各键齿所承受的作用力，如图6所示。

端面花键齿单个齿面的受力情况，如图7、8所示。

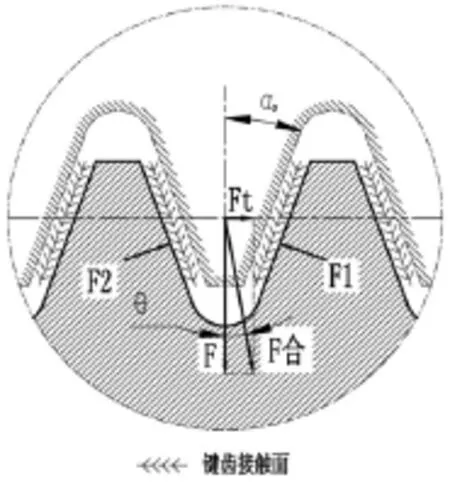
图7 端面花键齿面受力示意图(θ≤αD)

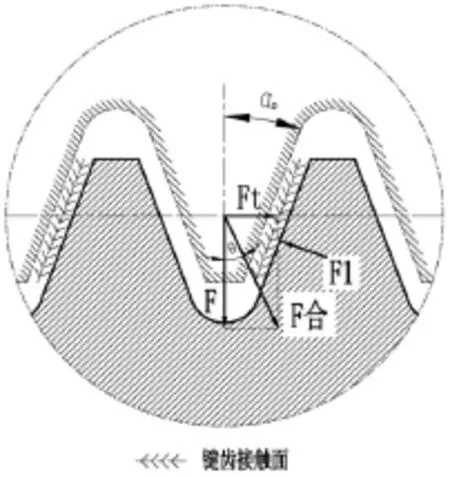
图8 端面花键齿面受力示意图(θ＞αD)

其中，F为端压力，Ft为名义切向力，F1为前齿面支反力，F2为后齿面支反力。

4 载荷计算

由于圆柱花键，只承载切向力，不承载径向的均匀压力。而端面键既承载切向力又承载端压力（如图7和图8所示），故齿面压力计算公式将较圆柱花键则有不同。由于端压力作用在整个端面齿上，方向垂直于端面花键齿端面，且切向力定义与圆柱花键一致，故齿面压力将由切向力和端压力的合力的方向确定，当端切夹角不大于齿面标准压力角时，端面齿啮合面前后齿面均承受压力。当端切夹角大于齿面标准压力角时，由于齿面贴合不能传递拉力，所以端面齿只有前啮合面单独承受压力，后齿面则不受力。故计算齿面单位载荷时将分两种情况分别进行计算。

（1）输入转矩T计算：T=9549·P/n

（2）名义切向力Ft计算：Ft=2000·T/(2R)

（3）端压力F计算：F=0.8·N·π/4·ds2·σs

（4）端切夹角：θ=arctg( Ft/F)

（5）端切夹角小于等于标准压力角时的压力和载荷计算：

①前齿面总压力F1'计算：

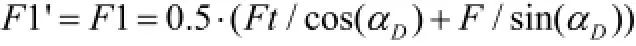
②后齿面总压力F2'计算：

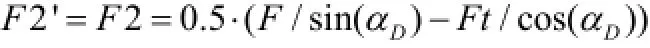
③前齿面单位载荷W1计算：W1=F1'/(Z·l)

④后齿面单位载荷W2计算：W2=F2'/(Z·l)

（6）端切夹角大于标准压力角时的压力和载荷计算：

①前齿面总压力F1'计算：

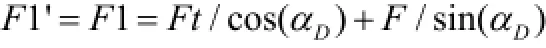
②后齿面总压力F2'计算：F2'=F2=0

③前齿面单位载荷W1计算：W1=F1'/(Z·l)

④后齿面单位载荷W2计算：20W=

（7）切向力引起的齿面弯曲应力计算。由于端压力在齿面的分布为前后对称，所以端压力在齿面表现形式以压力为主，对齿面弯曲的贡献甚微。切向力的作用方向是始终沿着齿的旋转前进方向，只在前齿面受力，表现主要以剪切和弯曲为主。而齿根弯曲则主要是由切向力引起，故本文参考文献[3]2.2弯曲应力计算方法，对单齿的受力做相应的假定简化：第一，切向力引起的均布载荷近似作用在前齿面整个面上；第二，将S'近似取值为最大弦齿厚；第三，将单个齿截面简化成矩形截面做截面系数分析，如图9所示。

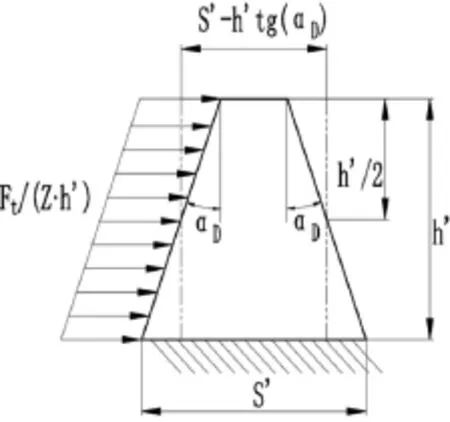
图9 单个齿面弯曲受力及简化示意图

则最大弦齿厚处的弯矩为：

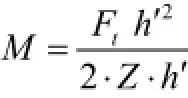
最大弦齿厚处截面系数为：

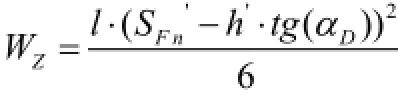
故最终弯曲应力为：

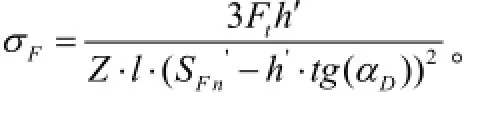
5 系数

（1）使用系数K1。参照GB/T17855-19995.1选取。

（2）齿侧间隙系数K2。从受力模型来看，端面花键齿的受力类似于GB/T17855-1999只承受转矩的情况，各齿在整个键齿圆盘面内同时受压，且端面花键齿具有自动定心的功能，所以也不会出现圆柱花键由相对位移使载荷分布在较小的键齿上的情况，也就没有圆柱内外花键的相对位移量。故选取K2=1.0。

（3）分配系数K3。参考文献[4]、[5]的描述，花键装配时，同时接触的齿数不应小于2/3。所以选取最小2/3的端面花键齿面接触，则K3=1/ (2/3)=1.5。

（4）轴向偏载系数K4。由于端面花键齿具有自动定心的功能，且采用紧固静联接，制造产生的齿向误差、安装后的同轴度误差以及受载后的扭转变形，均对轴向偏载影响较小，故选取K4=1.0。

（5）齿面接触强度的计算安全系数SH。按照GB/T17855-1999表1,序22选取。

（6）弯曲强度的计算安全系数SF。参照GB/ T17855-1999表1，序30选取。由于端面花键齿的齿形和受力模型与渐开线花键更为类似，故本文选取SF=1.25。

（7）作用直径dh计算系数K。参照GB/ T17855-1999表6中K值选取。本文参照渐开线花键进行选取。

6 承载力计算

6.1 齿面接触强度计算

（1）前齿面压应力：

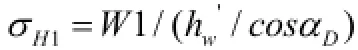
（2）后齿面压应力：

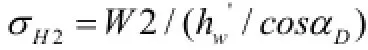
（3）齿面许用压应力：

（4）计算结果应满足下列条件：

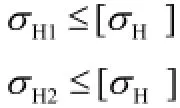
6.2 齿根弯曲强度计算

（1）齿根弯曲应力：

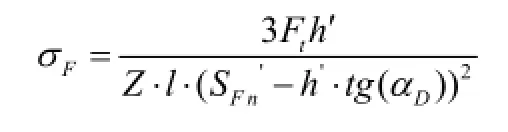
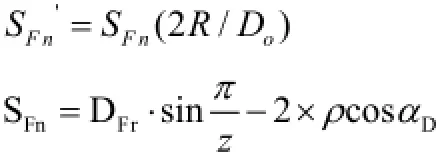
其中：SFn选取端面花键齿外侧圆柱面上齿根过渡曲线上的最小齿厚，该项选取齿根倒圆与齿侧相交处弦齿厚度。

（2）许用弯曲应力：

（3）计算结果应满足下列条件：σF≤[σF]

6.3 齿根剪切强度计算

（1）齿根最大扭转剪切应力

（2）许用剪切应力：[τF]=[σF]/2

（3）计算结果应满足下列条件：τF≤[τF]

6.4 扭转和弯曲强度计算

（1）当量应力：

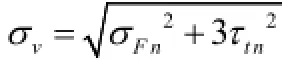
（2）许用应力：

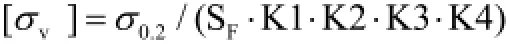
（3）计算结果应满足下列条件：σv≤[σv]

6.5 其它

鉴于端面花键齿正常工作过程中齿面之间无相对运动和位移，即不发生研磨，故可不对齿面耐磨损能力进行计算。

7 算例

本文以某实际应用的万向联轴器的端面花键齿承载能力为例。该万向联轴器实际运转输入功率为2500kW，额定转速为13.94r/min。该联轴器和其中的端面花键均符合文献[1]SWC780BF的要求。计算过程如下。

7.1 基础数据输入（表2）

7.2 相关数据推导（表3）

7.3 输入转矩T计算

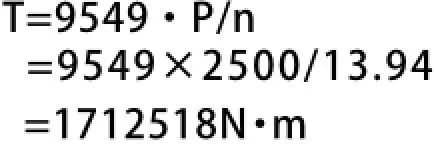
鉴于该计算出的实际输入转矩小于文献[1] SWC780BF中的公称转矩3300kN·m，本文按照设计承载最大工况考虑，在算例中均采用公称转矩计算。

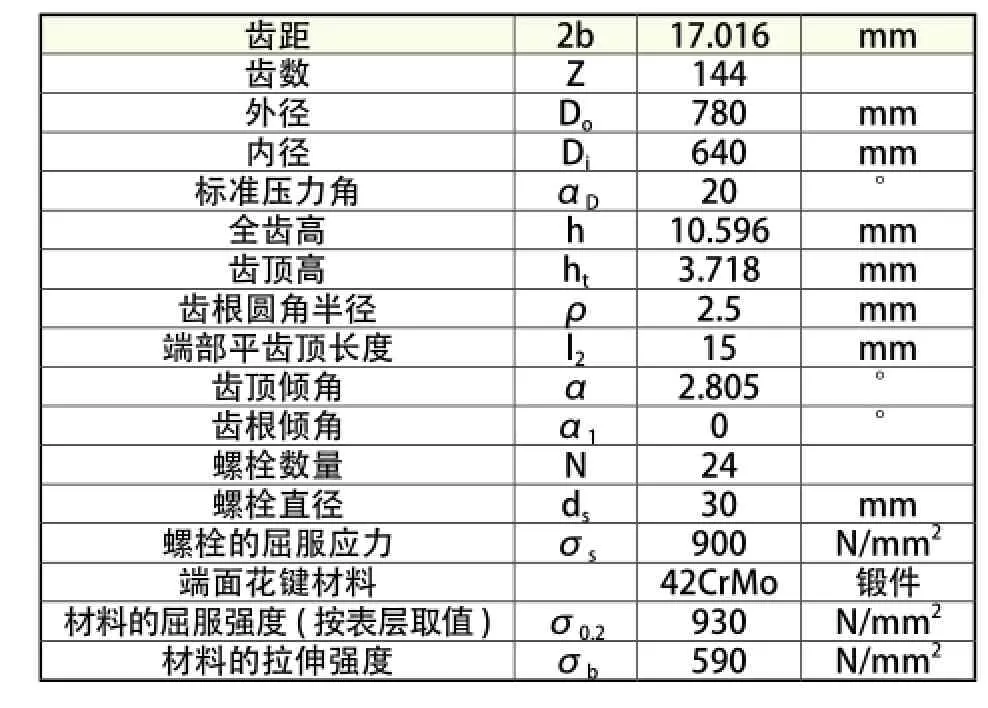
表2

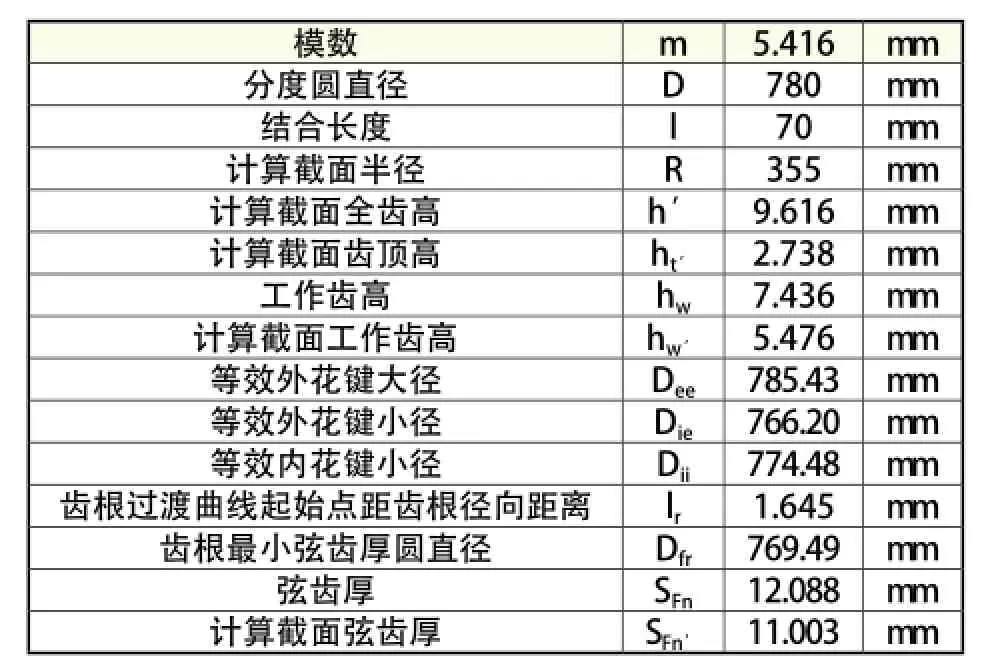
表3

7.4 名义切向力Ft计算

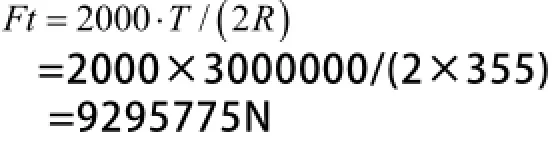
7.5 端压力F计算

7.6 端切夹角度

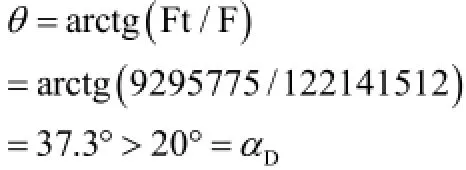
（1）前齿面总压力F1'计算。

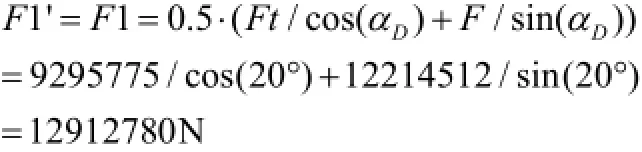
（2）后齿面总压力F2'计算：F2'=F2=0

（3）前齿面单位载荷W1计算：

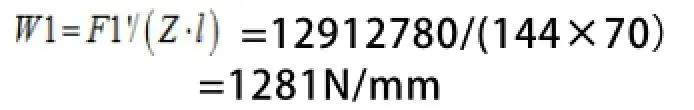
（4）后齿面单位载荷W2计算：W2=0。

7.7 使用系数K1

按照原动机均匀平稳，工作机中等冲击选取K1=1.25。

7.8 齿侧间隙系数K2

K2=1.0。

7.9 分配系数K3

K3=1.50。

7.10 轴向偏载系数K4

K4=1.0。

7.11 齿面接触强度的计算安全系数SH

按照较重要的及淬火的花键选取SH=1.5。

7.12 弯曲强度的计算安全系数SF

SF=1.25。

7.13 作用直径dh计算系数K

选取K=0.15。

7.14 齿面接触强度计算

（1）前齿面压应力：

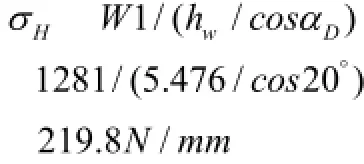
（2）后齿面压应力：σH2=0

（3）齿面许用压应力：

（4）计算结果应满足下列条件：

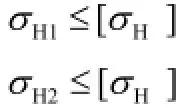
满足上述条件，安全。

7.15 齿根弯曲强度计算

（1）齿根弯曲应力：

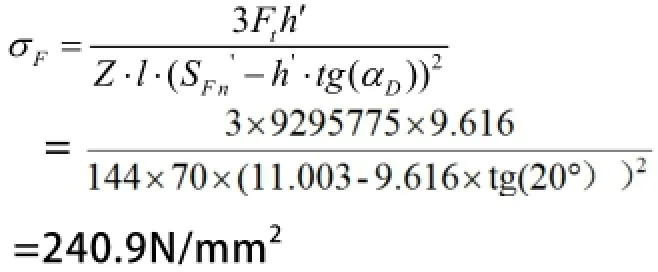
（2）许用弯曲应力：

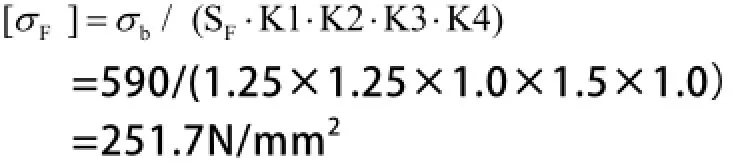
（3）计算结果应满足下列条件：σF≤[σF]

满足上述条件，安全。

7.16 齿根剪切强度计算

（1）齿根最大扭转剪切应力

（2）许用剪切应力

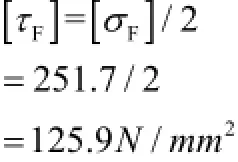
（3）计算结果应满足下列条件：τF≤[τF]满足上述条件，安全。

7.17 扭转和弯曲强度计算

（1）当量应力：

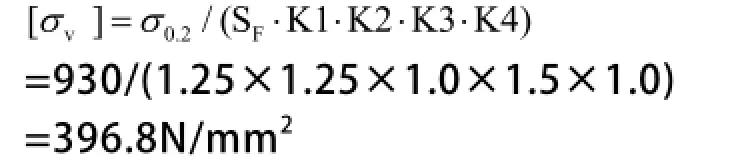
（2）许用应力：（3）计算结果应满足下列条件：σv≤[σv]满足上述条件，安全。

8 算例验证

8.1 通用简单算法的压应力验证

参见机械设计手册，第6篇，第3章，2.2.1通用简单算法公式：

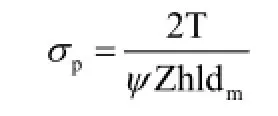
其中ψ为各齿间载荷不均匀系数，取值为0.7。以算例中SWC780BF为例，对齿面压应力进行验算，将压应力计算值进行比较，详见表4。

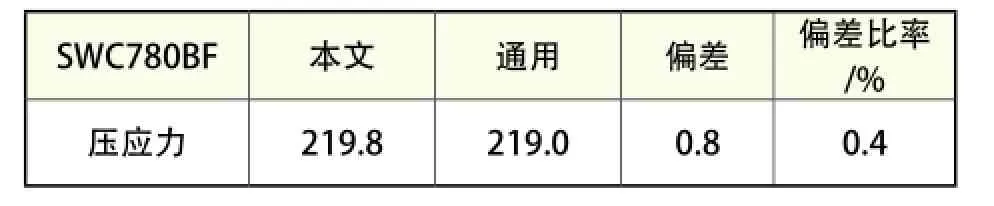
表4 压应力计算值比较汇总 N/mm2

通过汇总和比较两种算法的计算值，本文算法计算的压力值较通用算法偏差0.8N/mm2，偏差比率为0.4%，故可以认为压应力计算结果两种方法基本一致。

8.2 有限元直接计算法的正应力和剪应力验证

将端面花键齿进行有限元建模，按照4.5和4.6计算的各单个齿面的压力。忽略切向力的径向变化，近似的将单个齿面的压力均布在接触齿齿面上进行加载。如图10所示。

图10 SWC780BF端面花键齿有限元建模和加载模型

经过计算，提取整个模型最大Vonmise正应力和齿根最大剪切力，并将其与齿根最大弯曲应力和齿根最大扭转剪切应力进行比较，汇总如表5。

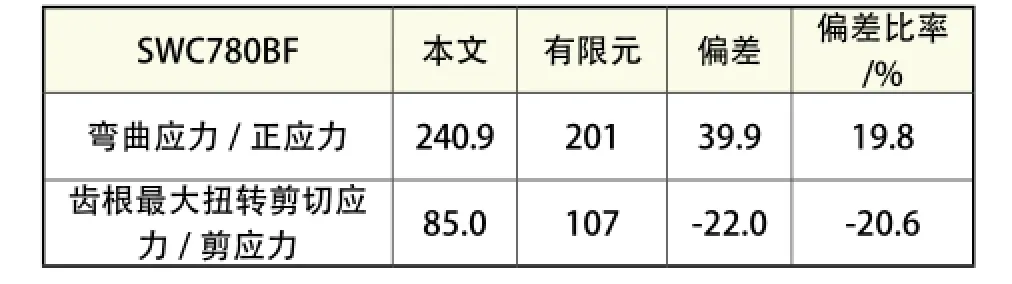
表5 正应力和剪切应力计算值比较汇总 N/mm2

通过上述比较可知，本文算法的齿根弯曲应力较有限元最大vonmise正应力结果偏大20%左右，齿根扭转最大剪切应力较有限元这与得到有限元结果最大剪切力计算结果偏小20%左右。

从计算的前提假设出发，分析上述本文齿根弯曲应力和齿根扭转最大剪切应力计算偏差的原因如下。

（1）本文齿根弯曲应力计算过程中是将键齿的梯形截面简化矩形截面进行计算，矩形截面的弯曲应力较梯形截面偏大，这与上述弯曲应力、正应力计算的结果相符。

（2）有限元计算方法因建模网格的不均匀以及在加载时忽略了切向力的径向变化等因素，故在有限元计算结果较真实结果通常存在一定的计算误差。

（3）本文齿根弯曲应力为矩形杆件受力模型，计算出来的是最大应力，而有限元最大Vonmise应力是基于第四强度理论下的正应力，它是基于剪切应变能的一种等效应力值，比对的参数略有不同。

综上分析，本文计算出的弯曲应力和齿根扭转最大剪切应力与有限元计算在许可的误差范围以内（通常选取20%，作为参考），即采用本文计算方法进行计算的结果是可信的。

9 结语

本文以端面花键齿SWC780BF为例，沿用《GB/ T 17855-1999花键承载能力计算方法》标准的思路，对端面花键齿的承载能力计算方法做了较为详尽的探讨。本文最终通过经验公式和有限元手段对该方法进行了验证，验证的结果与本文方法计算的结果基本一致。本文方法在一定程度上延伸了《GB/T 17855-1999花键承载能力计算方法》标准的使用范围，在今后工程应用中，可以采用本文方法对端面花键的承载能力计算进行指导。

[1]JB/T 5513-2006 SWC型整体叉头十字轴式万向联轴器: 30.

[2]GB/T 10026.1-2003锥齿轮承载能力计算方法 第1部分概述和通用影响系数:15.

[3]田茂权 端面花键齿参数设计及计算方法研究探索创新交流.中国航空学会青年科技论坛文集:699-700.

[4]GB50231-2009机械设备安装工程施工及验收通用规范:20.

[5]JB/T 5000.10-2007 重型机械通用技术条件 装配:2.

[6]机械设计手册. 第2卷/机械设计手册编委会编著.3版.北京：机械工业出版社, 2004.8:6-132.

TH131.4

A

1671-0711（2017）04（下）-0095-07