基于异步采样的多回路网络控制系统的建模与控制

王 冲,樊卫华,何 俊,周维维

(南京理工大学 自动化学院，南京 210094)

基于异步采样的多回路网络控制系统的建模与控制

王 冲,樊卫华,何 俊,周维维

(南京理工大学 自动化学院，南京 210094)

针对异步采样机制下的多回路网络控制系统，研究了系统的建模与控制器设计问题;首先，分析了同步采样机制引起的数据冲突等问题，提出了多传感器异步采样的传输机制;考虑固定的网络传输时延，将多回路网络控制系统建模为一类具有时延的离散线性系统；考虑同步控制要求，设计了基于一致性的控制策略，并利用Lyapunov函数法，给出了闭环系统渐近稳定的充分条件；应用锥补线性化方法(CCL)，给出了状态反馈控制器设计方法;最后的数值算例验证了上述方法的有效性。

多回路;网络控制系统;异步采样;离散模型;锥补线性化

0 引言

多输入多输出网络控制系统(MIMO NCS)是指一类具有分散的多个传感器节点、执行器节点和控制器节点，通过网络构成的闭环控制系统。MIMO NCS中由于数据通过网络在控制系统各部件之间进行传输和交换，网络的串行通信特性给控制系统的分析与设计带来了若干优势的同时，也导致了新的问题。例如，同一时刻采样的传感器节点数据无法同时到达控制器节点，有时某些传感器节点因无法获得网络资源而导致数据失效，这样控制器节点无法使用最新的采样数据计算控制量，使得系统稳定性和其它性能下降。相对于具有单一传感器节点的网络控制系统，MIMONCS的情况更为复杂，其传感器节点不仅需与自身系统的其它传感器节点竞争网络资源，还需与系统外的节点(与控制无关的节点)竞争网络资源。因而系统的分析与设计也显得更为复杂。

近年来，MIMO NCS已引起国内外研究人员的广泛关注，并取得了一系列的研究成果[1-3]。文献[4]研究了一类MIMO NCS的调度与控制协同设计，将可有效减小网络负荷的死区调度算法用于NCS，给出了系统渐近稳定的充分条件。文献[5-6]针对存在数据包丢失情形的MIMONCS，分别研究了最优滤波和H∞滤波方法，并给出了系统稳定的充分条件。以上文献主要针对NCS的被控对象是MIMO的，只存在一个控制器节点的情形。

相对于上述MIMONCS，应用更为广泛的是多回路NCS。即系统由多个具有相互耦合或约束的子系统组成的NCS。多回路NCS在实际应用中比较常见，如工业生产流水线上的多机器人系统、长距离传送带，汽车内的分布式自动控制系统等。文献[7]将一类具有随机丢包的多回路NCS建模为动态开关系统，给出了系统稳定的判别方法。文献[8]提出了一种传感器、控制器周期相同的异步采样控制系统，相对于大多数研究采用的同步采样方式，这种异步采样更接近于工程实现，但该文章并未涉及稳定性与控制器的研究。文献[9]在文献[8]的基础上提出了一种使系统稳定的控制器设计方法。文献[10]提出了一种新的传输机制，即传感器数据和控制器数据一个采样周期内不同时间段内传输，并给出了该机制下NCS的数学模型，但未涉及控制器设计。文献[11]给出了一种基于异步事件触发的NCS模型及系统稳定的充分条件，但其研究方法和结果都较为复杂。上述多回路NCS的研究结果多关注于稳定性，对其他用户需求的性能和控制要求，如一致性、跟踪性能等涉及不多。实际上，在很多的实际系统中，多个子系统的一致性是保证大系统能够正常工作的必要条件。如多机器人系统中，如果多个机器人的工作无法实现一致(即动作同步)，轻则影响产品的加工精度，严重的将使得产品成为废品。因此，一致性的研究应引起关注。

本文研究多回路网络控制系统的建模与控制问题。首先在分析同步采样与异步采样机制优缺点的基础上，确定了将异步采样和传输机制应用于NCS；随后，考虑存在网络诱导时延的情形，给出了NCS系统的数学模型；在此，构造了基于一致性要求的分布式控制律，并研究了系统的稳定性和控制器设计方法；最后，利用数值算例仿真验证了方法的可行性。

1 问题描述

本文研究的多回路NCS如图1所示。系统由n个子系统组成，子系统的传感器和控制器通过共用的网络进行数据传输与交换。

图1 多回路网络控制系统结构图

NCS中，传感器节点作为网络的智能节点，其工作方式常采用时间驱动。对于多回路NCS而言，多个传感器节点的时间驱动模式，可供选择的方式有同步采样或异步采样。所谓同步采样是指各个子系统传感器节点在统一的时刻进行采样并传输数据，而异步采样是指在各个传感器的采样时刻存在一定的间隔。同步采样机制是传统计算机控制MIMO对象时的常用工作方式，但应用于NCS中会导致在同一时刻多个节点同时竞争总线资源以发送数据，从而带来不确定网络诱导时延、数据包丢失等不利因素。而异步采样机制下，各传感器节点的采样时刻存在时间差，因而可以很大程度上，可以利用时间差完成数据的传输，从而避免因总线竞争导致的诸多不利用因素，更有利于系统系能及设计。

综合NCS的特性，本文所采用的异步采样机制具体的方法为：将整个系统的采样周期T分为n个时段(n为子系统个数)，并将其分配给各子系统；每个子系统在时段到来时进行采样，因此子系统采样的时间差为T0=T/n。且约定在一个时间片T0内，只允许一个子系统进行数据传输。这样可以最大程度地避免冲突的发生，减少因网络导致的不利因素。

下面，首先讨论异步采样机制下，系统的模型描述。不失一般性，给出如下假设：

假设2：传感器节点采用时间驱动，采样周期为T，控制器节点和执行器节点均采用事件驱动。

假设3：所有节点数据均采用单包传输，且传输过程中无数据包丢失。

设第i个子系统的状态方程描述为：

(1)

(2)

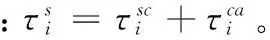
图2 多回路NCS的时序图

由式(1)、(2)，对第i个子回路离散化，可得:

(3)

其中:

为方便描述，记k:=tk。由式(3)可得NCS被控对象的离散状态方程为：

(4)

其中:

B=diag{B1,B2,…,Bn}，

D=diag{D1,D2,…,Dn}，

针对如式(4)所描述的多回路NCS，除满足稳定的基本要求之外，本文考虑各个子系统之间应满足一致性要求，即:

∀i,j∈1,2,…,n

由此，结合参考文献[12]及图2，设本文的系统采用如图3所示的拓扑结构，其中R为参考输入信号，并设控制律为：

ui=ki(xi-xi-1)+Nr·r

(5)

其中:ki为第i个子系统的状态反馈增益，Nr是参考输入增益，其目的是减小系统跟踪误差。

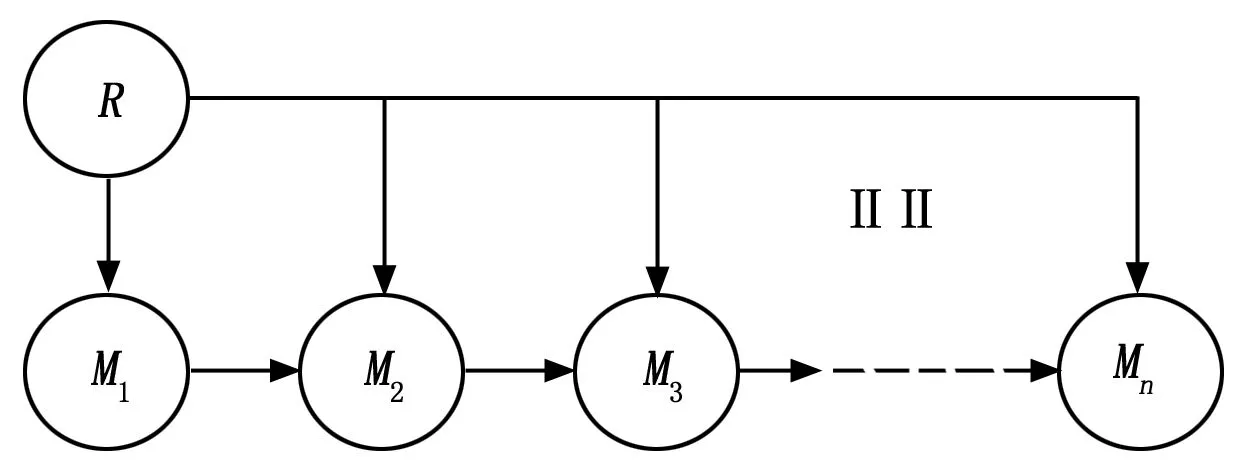
图3 控制器拓扑结构图

注1：式(5)描述的控制律利用的信息不仅是本子系统的采样信息，还包括临近子系统的信息，这样不仅使得各个子系统获得预期的跟踪控制目标，还可以兼顾临近子系统受到外界扰动时，系统输出(状态)发生突变时，系统仍能保持一致性。

(6)

根据式(3)的推导过程，可得：

(7)

将式(6)代入式(7)，可得：

(8)

因此有：

U(k)=KHYX(k)+KHΦBU(k-1)

(9)

由式(4)和式(9)，可得：

(10)

其中:L1=ΨB+ΛD，L2=ΓB-ΛD。

定义增广向量Z(k)=[XT(k),UT(k-1)]T，则有:

(11)

其中:A,B,H,Φ为确定性参数。

进一步根据本文采用的异步采样机制，各个回路的数据传输不会产生冲突，当数据包大小及传输速率为固定时，可获得传输时延τs的大小，从而Y,L1,L2也可通过计算获得，此时式所描述的系统是一个参数确定的离散线性系统。

本文研究的主要问题为：针对如式(11)描述的系统，设计如式所示的状态反馈控制器，使得系统渐近稳定。

2 稳定性分析

首先给出本文所用的引理：

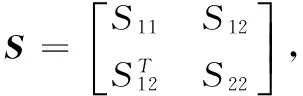
1)S<0

定理1：若存在对称正定矩阵P1,P2,和矩阵K，使得以下矩阵不等式成立：

(12)

则闭环系统(11)是渐近稳定的。

证明：取Lyapunov函数:

ΔV(k)=>V(k+1)-V(k)=

Z(k)=ZT(k)ΠZ(k)

其中:

由Lyapunov稳定性理论，若ΔV(k)<0，也即Π<0，则系统是渐近稳定的。

由引理1，Π<0等价于：

(13)

对上式做合同变换，左右两端同时乘以diag{I,I,P1,P2}，即可得求式(12)，证毕。

3 控制器设计

给定矩阵K，式为线性矩阵不等式，可利用MATLAB的LMI工具性求解，由此判断系统的稳定性。当K为待求解参数时，式(12)实际上是双线性矩阵不等式，无法直接利用LMI进行求解，且无法利用变量替换等常规方法使其转化为LMI。

本文采用锥补线性化方法[13]，将式(13)描述的非线性问题转化为线性矩阵不等式的优化问题，以此求解控制器参数。

定理2：若存在对称正定矩阵P1,P2，及式中定义形式的矩阵K，使得以下优化问题有解：

(14)

其中:

(15)

(16)

(17)

则闭环系统(11)是渐近稳定的。

证明过程略。

以下给出控制器增益的具体求解步骤：

算法1：

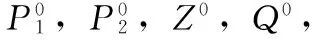
步骤2：对于矩阵变量(P1,P2,Z,Q)求解如下问题：

s.t.式(15)、(16)和(17)成立。

步骤3：将步骤2求得解带入式(13)中验证是否成立，如果成立，则上述解即为一组可行解。若不成立则继续转到步骤2进行计算，直至达到迭代上界，则系统无解。

4 数值算例

设如图1所示的NCS，由4个子系统组成，子系统的状态方程描述如下：且:

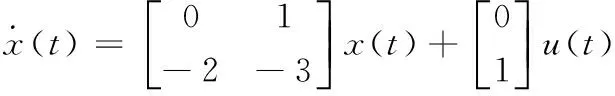
设采样周期为T=10 ms，则时间片长度T0=T/4=2.5 ms。网络速率为200 Kbps，数据包长度为80 bit。由此可得传输时延τs=0.8ms。

根据定义分别求得A,B,D,Γ,Λ,Ψ,Y,Φ如下：

利用MATLAB的LMI工具箱，根据算法1求解可得：

控制律为：K=diag{k1,k2,k3,k4}

其中:

k1=[-0.0486-0.0570],k2=[-0.3356-0.4363],

k3=[-0.2079-0.2695],k4=[-0.064-0.0293]

利用Truetime2.0工具箱搭建网络控制系统仿真系统。并设各个子系统初值分别为：

x1=[2.0-0.5]T,x2=[2.00.5]T,

x3=[-2.0-0.5]T,x4=[-2.00.5]T

在零输入情况下，系统的状态响应曲线如图4所示，显然各子系统是渐近稳定的。

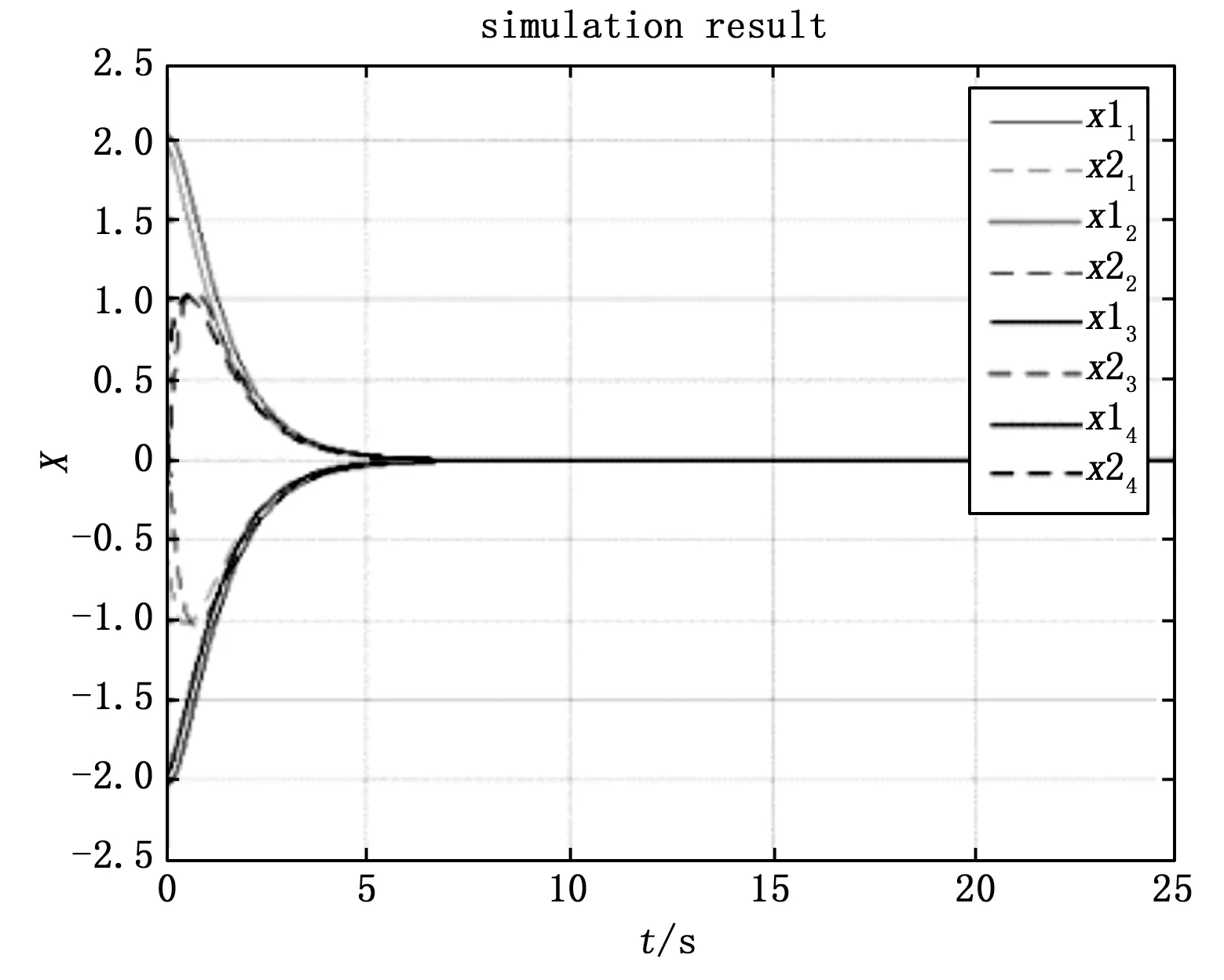
图4 系统状态响应曲线

图5所示为网络中各个节点占用总线的情况，可以看到每个回路在时间T0内完成数据传输，几乎没有数据包冲突和总线竞争情况。

图5 网络调度示意图

系统在上述初始条件下给予如下的参考输入信号：

系统的输出响应如图6所示，图7为子系统之间的状态差值曲线，结果表明在所设计的控制器作用下，各个子系统基本可以跟踪输入信号，能够满足一定的一致性指标。

图6 阶跃响应状态曲线

图7 子系统状态误差

5 结论

1) 通过异步采样方式可以有效地避免冲突并且可以使得数据按照预定的方式有序传输。

2) 根据传感器异步采样方法对多回路网络控制系统建立的数学模型是有效的，并且提出的控制器设计方法可以满足稳定性要求。

3)设计的一致性的状态反馈控制器，可以达到多回路网络控制系统的一致性要求。

本文提出的一致性控制器贴近实际工程，可以直接应用于多电机同步系统，具有理论和应用价值。

[1] 刘鲁源，吕伟杰，陈玉柱.MIMO网络控制系统的稳定性分析[J]. 信息与控制, 2006, 35(03):393-396.

[2] 魏利胜，江 明，宋 杨，等.MIMO网络控制系统调度方法及稳定性研究[A]. 2009中国控制与决策会议论文集[C]. 2009.

[3]LiJ,ZhangQ,YuH,etal.Real-timeguaranteedcostcontrolofMIMOnetworkedcontrolsystemswithpacketdisordering[J].JournalofProcessControl, 2011, 21(6): 967-975.

[4]XieR,FanW,ChenQ.DesignandoptimalcontrolforMIMOnetworkedcontrolsystemsbasedondeadbandschedulingstrategy[A].ControlConference(CCC), 2015 34thChinese[C].IEEE, 2015: 6734-6739.

[5]YangF,WangW,NiuY,etal.Observer-basedH∞,controlfornetworkedsystemswithconsecutivepacketdelaysandlosses[J].InternationalJournalofControlAutomation&Systems, 2010, 8(4):769-775.

[6]SahebsaraM,ChenT,ShahSL.Optimalfilteringinnetworkedcontrolsystemswithmultiplepacketdropout[J].IEEETransactionsonAutomaticControl, 2007, 52(8): 1508-1513.

[7]DuD,FeiM,JiaT.ModelingandstabilityanalysisofMIMOnetworkedcontrolsystemswithmulti-channelrandompacketlosses[J].TransactionsoftheInstituteofMeasurementandControl, 2011: 0142331211406605.

[8]LianFL,MoyneJ,TilburyD.Analysisandmodelingofnetworkedcontrolsystems:MIMOcasewithmultipletimedelays[A].AmericanControlConference, 2001.Proceedingsofthe2001[C].IEEE, 2001, 6: 4306-4312.

[9]JinrongF.Analysisanddesignofthestabilityforanasynchronousnetworkedcontrolsystems[A].Proceedingsofthe2ndinternationalAsiaconferenceonInformaticsincontrol,automationandrobotics-Volume1[C].IEEEPress, 2010: 9-12.

[10]SongH,YuL,ZhangWA.Stabilizationofnetworkedcontrolsystemswithcommunicationconstraintsandpacketdropouts[A].CDC[C]. 2009: 7936-7941.

[11]WangX,SunY,HovakimyanN.Asynchronoustaskexecutioninnetworkedcontrolsystemsusingdecentralizedevent-triggering[J].Systems&ControlLetters, 2012, 61(9): 936-944.

[12]FanW,XieL,XieR.DistributedcontrolofMIMOnetworkedcontrolsystemswithtime-triggeredprotocol[A].ControlConference(CCC), 2014 33rdChinese[C].IEEE, 2014: 5760-5765.

[13]LaurentElGhaoui,FrancoisQustry,MustaphaAitRami.Aconecomplementaritylinearizationalgorithmforstaticoutput-feedbackandrelatedproblems[J].IEEEtransonAutomaticControl, 1997, 42(8): 1171-1176.

ModelingandControllerDesignofNetworkedControlSystemswithMultipleLoopsBasedonAsynchronousSampling

WangChong,FanWeihua,HeJun,ZhouWeiwei

(SchoolofAutomation,NanjingUniversityofScienceandTechnology,Nanjing210094China)

The modeling and controller design of multi-loop network control systems under asynchronous sampling mechanism is studied. Firstly, the data collision problem caused by synchronous sampling mechanism is analyzed. Then, the asynchronous sampling and transmission mechanism about the sensors is proposed. A discrete model with delay is built according to the multi-loop NCS with fixed time delay. Considering the requirements of synchronization performance, the control strategy based on consistency is designed.Based on the Lyapunov stability theory and linear matrix inequality method, the sufficient condition for asymptotic stability is presented. Then by applying the Cone Complementarity Linearization (CCL) method, the status feedback controller is designed. Finally, a numerical example is given to illustrate the effectiveness of the proposed method.

multi-loop;NCS;asynchronous sampling; discrete model;CCL

2016-11-05；

2016-11-25。

国家自然科学基金项目(61673219)；江苏省"六大人才高峰"项目(XNYQC-CXTD-001)。

王 冲(1990-)，男，河北蠡县人，硕士研究生，主要从事网络控制系统理论方向的研究。

1671-4598(2017)04-0061-05DOI：10.16526/j.cnki.11-4762/tp

TP

A