Cooperative Jamming for Enhancing Security of Cognitive Radio Networks with Multiple Primary Users

Xiaofeng Feng, Xinbo Gao , Ru Zong

State Key Laboratory of Integrated Services Networks, School of Electronic Engineering, Xidian University, Xi’an 710071, China

* The corresponding author, email： xbgao@mail.xidian.edu.cn

I. INTRODUCTION

Recently, cognitive radio (CR) has been proposed and regarded as a promising technique to solve the spectrum shortage problem or to improve the spectrum efficiency in future wireless communication systems [1, 2]. In a cognitive radio networks (CRNs), secondary user (SU) is allowed to access to the licensed spectrum of the primary user (PU), while the interference power generated by the SU does not interfere with the PU’s communications.Moreover, security is an important requirement for future wireless communications networks, and CRN is critical as it is easily exposed to external threats [3-6], such as eavesdropping [7].

Traditionally, the security is dealt with cryptographic method at upper layers [8].However, the cryptographic methods rely on the computational hardness on decrypting the message to achieve security. As the computational power increases, the computational hardness of certain mathematical problems may no longer hold, causing many current cryptosystems to break down. As a solution to support and supplement existing cryptographic protocols, physical layer security (PLS) has attracted much more attention in academia community [9-12]. The main idea behind PLS is to exploit the wireless channel characteristics to improve the security of wireless transmission.This security is quanti fied through the notion of secrecy rate, which is defined as the rate of secret information sent from a source to its destination without being tapped in by malicious eavesdroppers.

However, the secrecy rate would be equal to zero when the source-destination channel is worse than the source-eavesdropper channel[13]. To overcome this limitation, cooperative jamming has been employed to improve the secrecy rate, in which appropriate jammer will be selected to impair eavesdropper’s ability to decode the source’s information through transmitting codewords [14-15] or noise [16] independent of the source message. Cooperative jamming was firstly proposed in [14], which be used to increase achievable rates in the scenarios where a general Gaussian multiple access wiretap channel and two-way wiretap channel were assumed, respectively. In [17-19], some cooperative jamming schemes are proposed to guarantee the security in wireless relay network. In these schemes, the sources,relays and even destinations can be used as helper to provide jamming signals to confuse the eavesdropper.

In CRNs, PU is the licensed user and has higher priorities for spectrum usage. SU has the requirement on data transmission,but do not has the right to use the spectrum.Therefore, in order to improve the secrecy rate obtained by PU, SU can be recruited as friendly jammer to cooperate with PU. As a compensation, SU can obtain some spectrum resource from PU for their own data transmission. Considering both of PU and SU are sel fish individual and not willing to cooperate unconditionally with each other, some corresponding cooperative jamming schemes have been studied. In [20] and [21], two cooperative schemes are proposed for CRNs, whereby the PU can cooperate with trustworthy SUs to enhance its security level and SUs can gain transmission opportunities. In [22] and [32], a game-theoretic mechanism and a QoS-aware auction framework are proposed for recruiting sel fish users as cooperative jammer to enhance secret communications, respectively. In [23],[31] and [33], three cooperative jamming schemes are proposed for CRNs, whereby a trustworthy SU with multiple antennas will creates interference on both primary and eavesdropping receivers, and an appropriately designed beamformer is proposed to maximize the secrecy rate of PU. In [24], a cooperation paradigm was proposed for CRNs, where cooperative simultaneous transmissions of PU and SU yield mutual bene fits in the presence of an eavesdropper.

A multi-leaders and single-follower Stackelberg game is proposed to model the interaction between multiple primary users and single secondary users.

However, all the above works only considered the simplify scenario with a single PU in their framework, which might not be sufficient to exploit the cooperation benefits in the whole network. In contrast, it will be more practical to consider the scenario with multiple PUs. In fact, the cooperation scheme for CRNs has been extended to the scenario with multiple PUs in some recent research. In[25], a cooperative scheme was proposed for a cognitive radio relay network with multiple PUs and multiple SUs, in which the minimum sum-rate requirement of all matched PUs and SUs is guaranteed. In [26], a SU assisted cooperative relaying mechanism in CRNs with multiple PUs was investigated, and a distributed matching algorithm which determines the matched pairs between PUs and SUs was proposed. In [27], a new cooperative scheme was proposed for cognitive radio relay networks with multiple PUs, in which PUs can achieve power saving due to cooperative relaying of SU. However, in all above of these works,SU takes on the role of a relay to improve the transmission rate of PU, and the secrecy rate of PU is not considered.

In this paper, we will consider a more complicated scenario with multiple PUs and try to investigate the cooperative jamming scheme between multiple PUs and a single SU for secure information transfer in CRNs. Considering the features of CRNs, the cooperation is performed on a mutual bene fit basis. Since the PU has the high priority on spectrum usage,the objective of cooperation is to maximize the secrecy rate of PU, given that the SU has the requirement on the transmission rate. In order to obtain more spectrum for data transmission, SU will takes on the role of a friendly jammer and cooperate with multiple PUs at the same time. As a compensation, multiple PUs will grant rewarding spectrum fraction to cooperating SU for their own transmission.Both PU and SU are considered as a selfish and rational individuals and have their own interest. In order to maximize its achievable transmission rate, SU needs to reasonably allocate its limited jamming power between multiple PUs according to all PU’s rewarding spectrum fraction.

Moreover, each PU will make their decision on rewarding spectrum fraction to compete for the limited jamming power, knowing that the SU’s jamming power allocation result is the function of all PUs’ decisions. Due to the jamming power allocated to each PU is not only affected by this PU’s decision but also affected by the rival’s decision, each PU has to consider the in fluence generated by rival in the optimal decision making process. As a result,the optimal decision making process of each PU becomes more complicated and difficult.

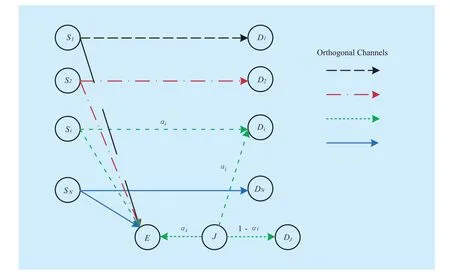
Fig. 1 System model of cooperative jamming in CRN with multiple PUs

Compared with the previous research works, our contributions are listed as the following.

● We propose a novel game-theoretical framework for recruiting the sel fish SU as the cooperative jammer of multiple PUs to enhance the secret communications in CRNs. Different from the scenario where only one PU is considered, the coming of more PUs brings new challenges into the cooperation paradigm.

● In order to analyse the behaviour of each user in the proposed scenario, the interaction between multiple PUs and SU is formulated as a multi-leaders and single-follower Stackelberg game. We prove the existence of equilibrium solution and present a Gauss-Jacobi iterative algorithm to compute a Stackelberg equilibrium solution.

● Numerical results show that under our proposed framework, both PU and SU can achieve better performance in terms of secrecy rate and transmission rate when doing cooperation.

The remainder of the paper is organized as follows. The detailed description of the system model is given in Section II. In Section III, a game-theoretic framework is proposed to formulate the competition among PUs and the interaction between PUs and the SU. And a Gauss-Jacobi iterative algorithm is presented to compute an equilibrium solution. Simulation results are provided in Section IV, followed by the conclusion in Section V.

II. SYSTEM MODEL

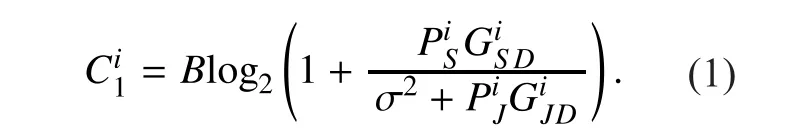
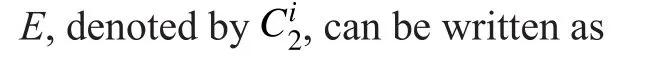
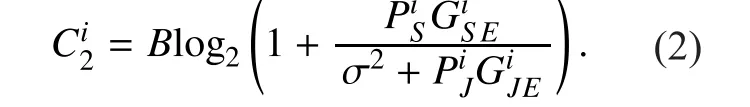
Then, the secrecy rate gained by PUican be de fined as

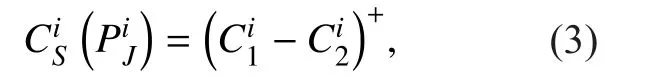
In many practical circumstances, eavesdropper is a passive attacker and becomes undetectable since the eavesdropper just overhears and interprets the CR transmission without transmitting any active signals. Therefore, the channel information between each PU and the malicious eavesdropper might not be known or accurately known. Under this condition, the secrecy capacity formula should be rewritten considering the uncertainty. In this paper, to simplify the analysis, we assume perfect channel information, which means all nodes have all channel information. This is a typical assumption in studying physical layer security.

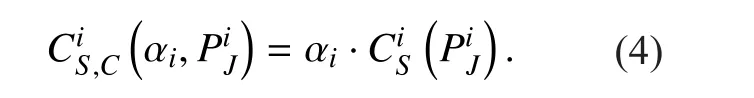
The overall achievable transmission rate of the SU is de fined as

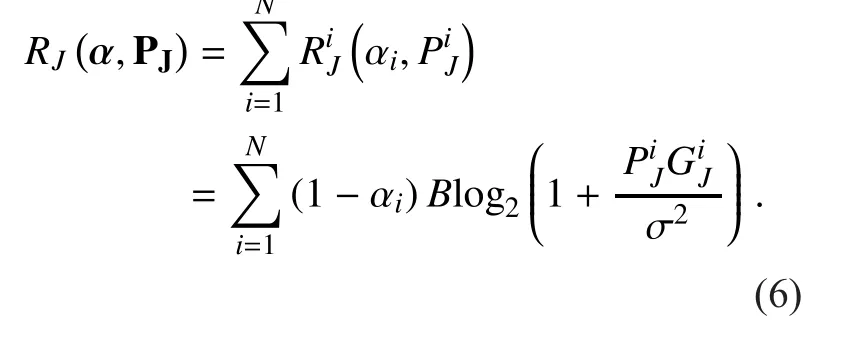
III. GAME-THEORETIC FRAMEWORK

In this section, we study how to use game theory to analyse cooperative between multiple PUs and a single SU in CRNs. In CRNs, both of PU and SU are considered as a rational and sel fish individuals, they always make decision independently to maximize their own utility.Moreover, since PU is the licensed user and has higher priority on spectrum usage, it has the ability to move first and determine the bandwidth fraction preserved for its secret communication. After observing PUs’ decisions, the SU will make the best reaction and decide the jamming power allocated to each PU.

As the actions occur sequentially, the Stackelberg game [28] provides a natural framework to model the interactions between PUs and SU. In a Stackelberg game, some players act as the leader and the others as the follower. The leader moves first, and is assumed to possess all necessary information about the follower’s possible reactions to the decisions taken by the leader. Then the follower observes the leader’s actions before reacting optimally to them. Obviously, in our paradigm,it is reasonable to make PU as the leader, and SU as the follower. Therefore, the interaction between PUs and SU can be formulated as a multi-leaders and single-follower Stackelberg game. Each leader anticipate the response of the followers, and uses this ability to select its strategy to compete with the other leaders in the Nash non-cooperative way.

3.1 Follower (SU) model

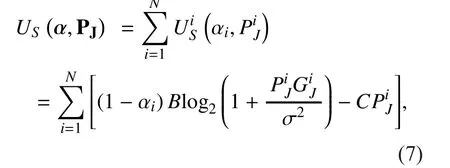
Notice that the first part of the utility (7)re flects the node’s satisfaction from accessing the spectrum, in terms of amount of data it can transmit, while the second part stands for its expense, in terms of power required to provide friendly jamming for each PU. We remark that the second part of utility needs not be constrained to a linear function, which is applied here for analytical convenience. Furthermore,notice that SU’s transmission is not subject to secrecy requirements.

Considering SU is a rational individual, the necessary condition that SU is willing to cooperate with PUiis

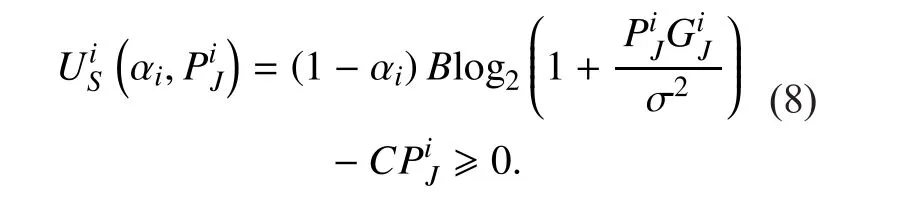
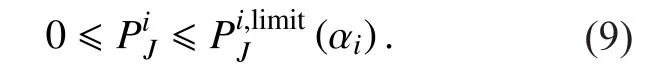
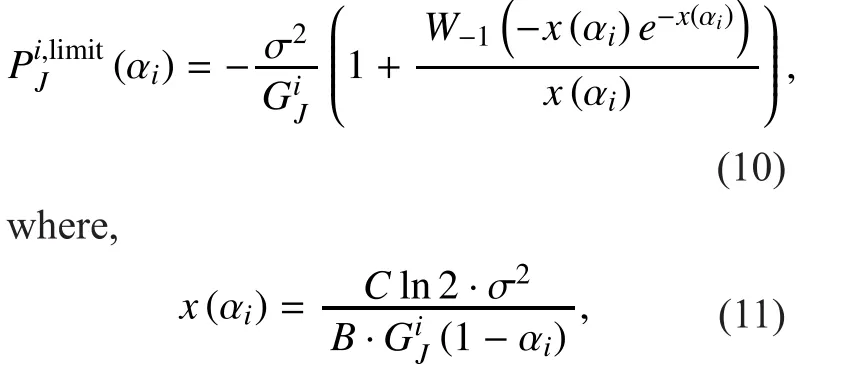
Then, the optimization problem for SU to make optimal strategy is formulated as

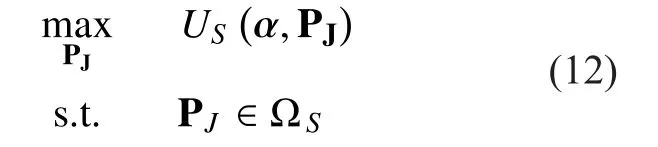
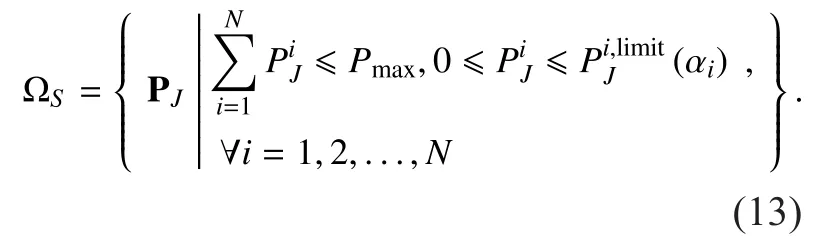
Now, for a given PUs’ strategy prois supposed as a solution of the optimization problem (12). Then, there is a multiplierso that the classicalKarush-Kuhn-Tucker(KKT)conditions [29]

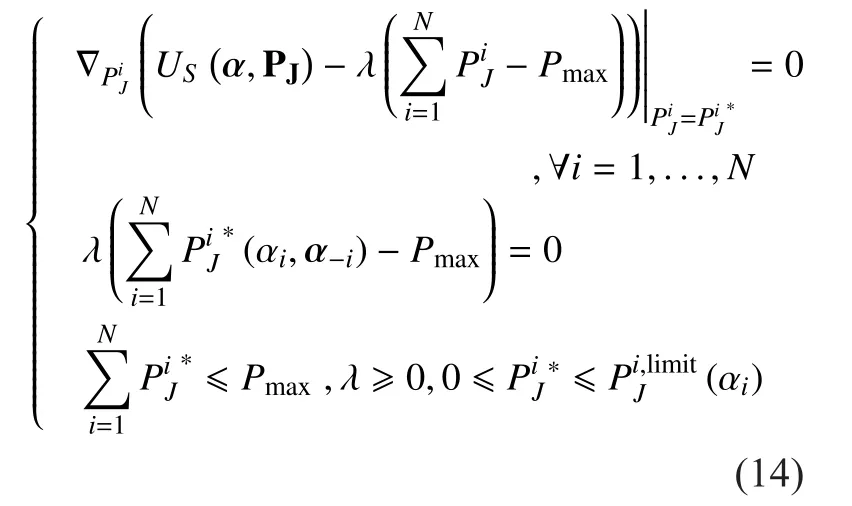
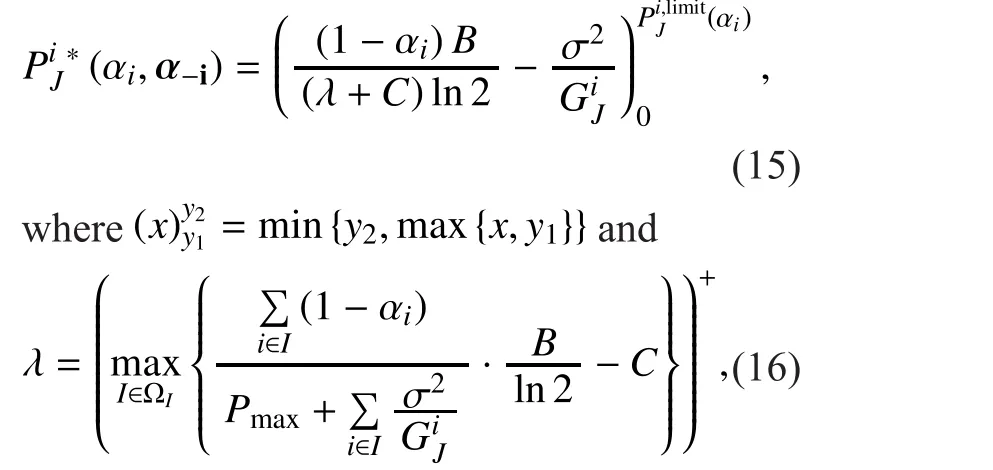
3.2 Leader (PU) Model

As the leader, each PU will first determine the optimal strategy, aiming to maximize its secrecy rate. Due to each PU knows that SU’s reaction is the function of all PUs’ strategies,they will anticipate the reaction of SU to their strategies and include the optimality condition and constraints into their utility function.Therefore, the utility function of PUican be denoted as

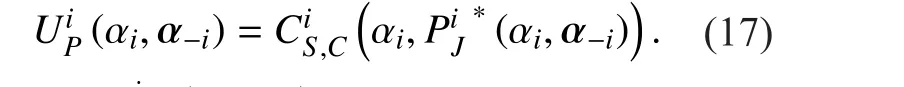
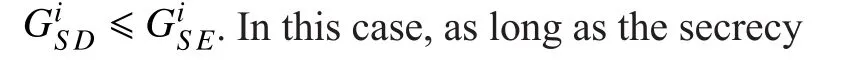
According to (4), in order to guarantee the secrecy rate obtained by PUiwith cooperative jamming is greater than zero, the following conditions need to be satis fied：

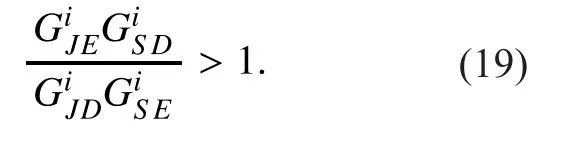
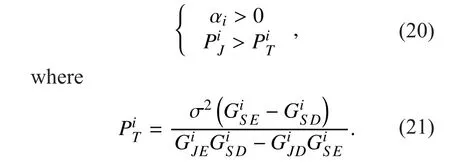
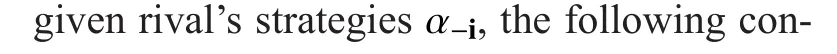
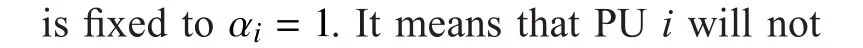
If the condition (19) is satis fied, substituting (15) into (20), the conditions (20) can be rewritten as follows：

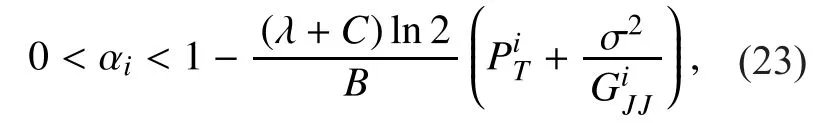
Now, substituting (15) and (23) into (18),the optimization problem can be reformulated as follows：

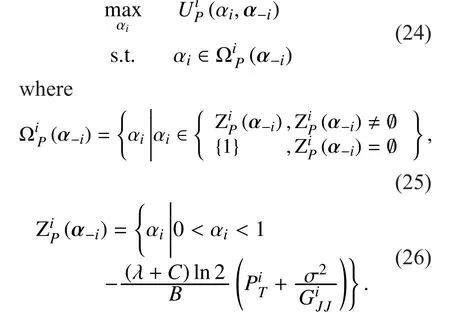
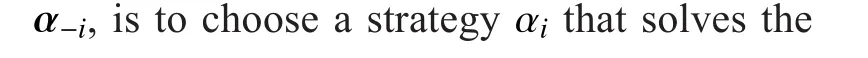
3.3 Existence of Stackelberg Equilibrium (SE)

According to the conclusion of previous section, we can know that the competition relationship between multiple PUs can be formulated as a GNEP. In this section, we will analyse the existence of equilibrium solution for our proposed multi-leaders and single-follower Stackelberg game. First, for the GNEP given by (24), the de finition of equilibrium is given as follows.

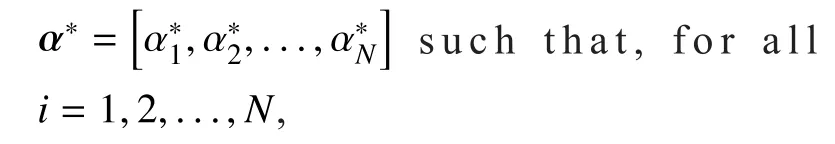
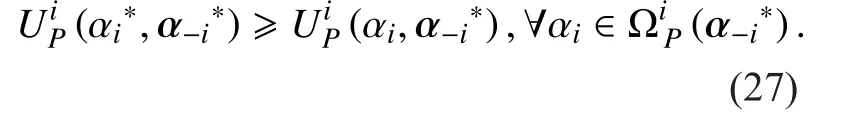
The outputs from Stackelberg game is theStackelberg Equilibrium(SE). The SE can be expressed as a pro file of equilibrium strategies over which each player will not deviate from the equilibrium. Next, the formal definition of the SE corresponding to our proposed multi-leaders and single-follower Stackelberg game is given below.

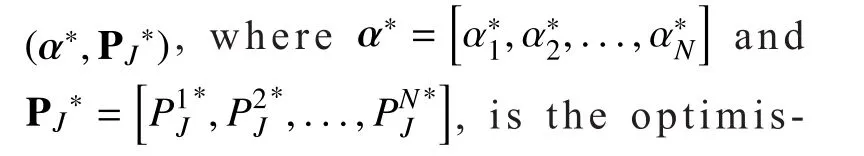
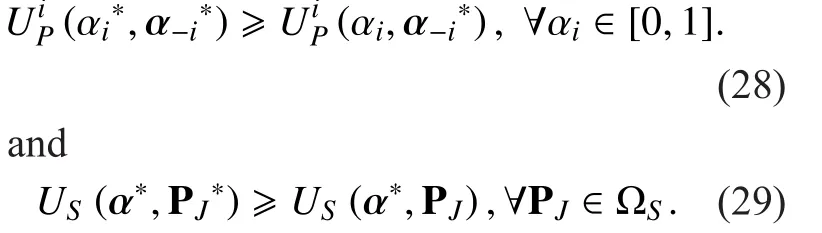
For a multi-leaders and single-follower Stackelberg game, the existence of SE is not always guaranteed. Now, we will analyse our proposed Stackelberg game and prove that when a certain condition satisfied, our proposed multi-leaders and single-follower Stackelberg game exist a SE.

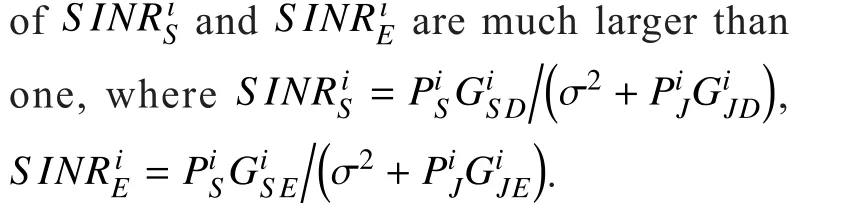
Proposition 1.If condition 1 is satisfied,

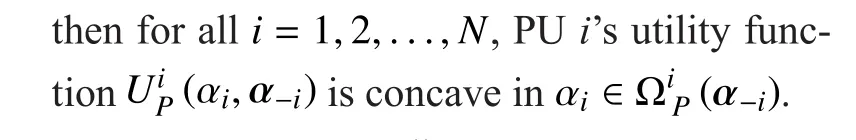
Proof： See Appendix.

Proposition 2.If condition 1 is satisfied,then our proposed multi-leaders and single-follower Stackelberg game exists a SE.

Proof： According to De finition 1 and De fimulti-leaders and single-follower Stackelberg game. It means that if the GNEP defined by(24) exists a GNE, then the proposed Stackelberg game also exists a SE.

According to Theorem 6 given by [30], for a given GNEP in which each player’s optimization problem is maximization problem, if each player’s object function is quasi-concave,and for an arbitrary given rival’s strategies,each player’s feasible strategy set is nonempty, closed and convex, then the given GNEP exists a GNE. As shown in Proposition 1, if Condition 1 satisfied, the object function of each PU in our proposed GNEP is concave.Therefore, it also a quasi-concave. Moreover,according to (25) and (26), we can see that each player’s feasible strategy set is a one dimensional range or single element set. Therefore, for a given rival’s strategies, each PU’s feasible strategy set is obviously nonempty,closed, and convex. Then, if Condition 1 is satis fied, the proposed GNEP de fined by (24)exists a GNE.

Therefore, if Condition 1 is satisfied, the proposed Stackelberg game also exists a SE.

3.4 Gauss-Jacobi Iterative Algorithm

Once the existence of SE is proved, the next question would be compute a SE. According to the analysis in Section 3.3, in order to compute a SE of the proposed Stackelberg game,a GNEP given by (24) needs to be solving firstly. Once a GNE solution is obtained, then it would be the final strategies accepted by all PUs.

Substituting the GNE into SU’s optimization problem given by (12), then the corresponding reaction strategy of SU also can be obtained through solving the given optimization problem. The GNE and the corresponding reaction strategy compose a SE of our proposed multi-leaders and single-follower Stackelberg game.

To solve the GNEP defined by (24), we present a classical Gauss-Jacobi iteration algorithm, as shown in Algorithm I. The main idea underlying this algorithm is to solve all player’s optimization problem in GNEP one by one. In the initialization phase, each PU needs to randomly choose an available strategy and announce it to other PUs. Once a PU knows all of its rival’s strategies, it can compute the optimal reaction strategy through solving the programing problem (24) and update its strategy according to the solution. Specially, at each time, only one PU’s optimization is solved,assuming that other PUs’ current strategies are still their previous strategies. After the strategy updating, if current strategy is different from the previous strategy, PU needs to broadcast its newest strategy. The above process will be repeated until none of PUs update its strategy.

Moreover, the convergence of Algorithm I cannot be guaranteed. But due to the implementation of Algorithm I is very easy, in the general case, the equilibrium solution can be found through repeated using Algorithm I.

?

IV. NUMERICAL RESULTS

To evaluate the performance of the proposed framework, we conduct the following simulations. For the sake of simplicity and without loss a generality, we consider a CRN with only five PUs (N=5), one SU, and one malicious eavesdropper. The coordinates of each node are shown in Figure 3. We assume that the distance between SUJand its destinationDJis fixed and equal to 20m. The other simulation parameters are

set up as follows： Each PU’s average transused.

Using the spectrum under different frequency range, the corresponding channel gain will also be different. Under different channel state,the corresponding Stackelberg equilibrium results and the utility of each player are shown in Fig. 3. As shown in Fig. 3(a), different channel state will lead to different equilibrium result. Each PU can adaptively adjust its equilibrium strategy according to channel state.Moreover, as shown in Fig. 3(b), due to the influence of channel gain, the PU who grant SU the biggest spectrum fraction does not necessarily obtain maximum jamming power allocation. We can also observed that as long as a PU participates in the cooperation, the secrecy rate obtained by this PU would be greater than zero, and SU can also obtain some spectrum fraction from this PU. When the secrecy rate obtained by a PU cannot be improved through cooperation with SU, PU will refuses to grant any spectrum to SU. Correspondingly, SU will not allocate any jamming power to this PU,and the final secrecy rate obtained by this PU would be equal to zero.

Next, in order to intuitively observe the reaction strategy and the final equilibrium results, we assume that only PU 1 and PU 2 are allowed to anticipate the game. In this case,when one PU changes its strategy, the optimal point to achieve the highest secrecy rate of other PU changes. The best response curve of both PUs are shown in Fig. 4(a). The best response curve re flects the best strategy selection under the given rival’s strategy. For example, the point (x,y) on PU1’s best response curve means that when PU2’s strategy isy,PU1 should selectxas its strategy to maximize its utility. As shown in Fig. 4(a), when PU 1 increases the spectrum fraction granted to SU, the spectrum fraction granted by PU 2 will also increase. The reason is that when the spectrum granted by PU 1 increases, SU will allocate more jamming power to PU 1, and subsequently the jamming power allocated to PU 2 will decreases. In order to obtain its desired jamming power, PU 2 has to increase the granted spectrum fraction. Moreover, we also can observed that different maximum available jamming power of SU will lead to different equilibrium strategy results.

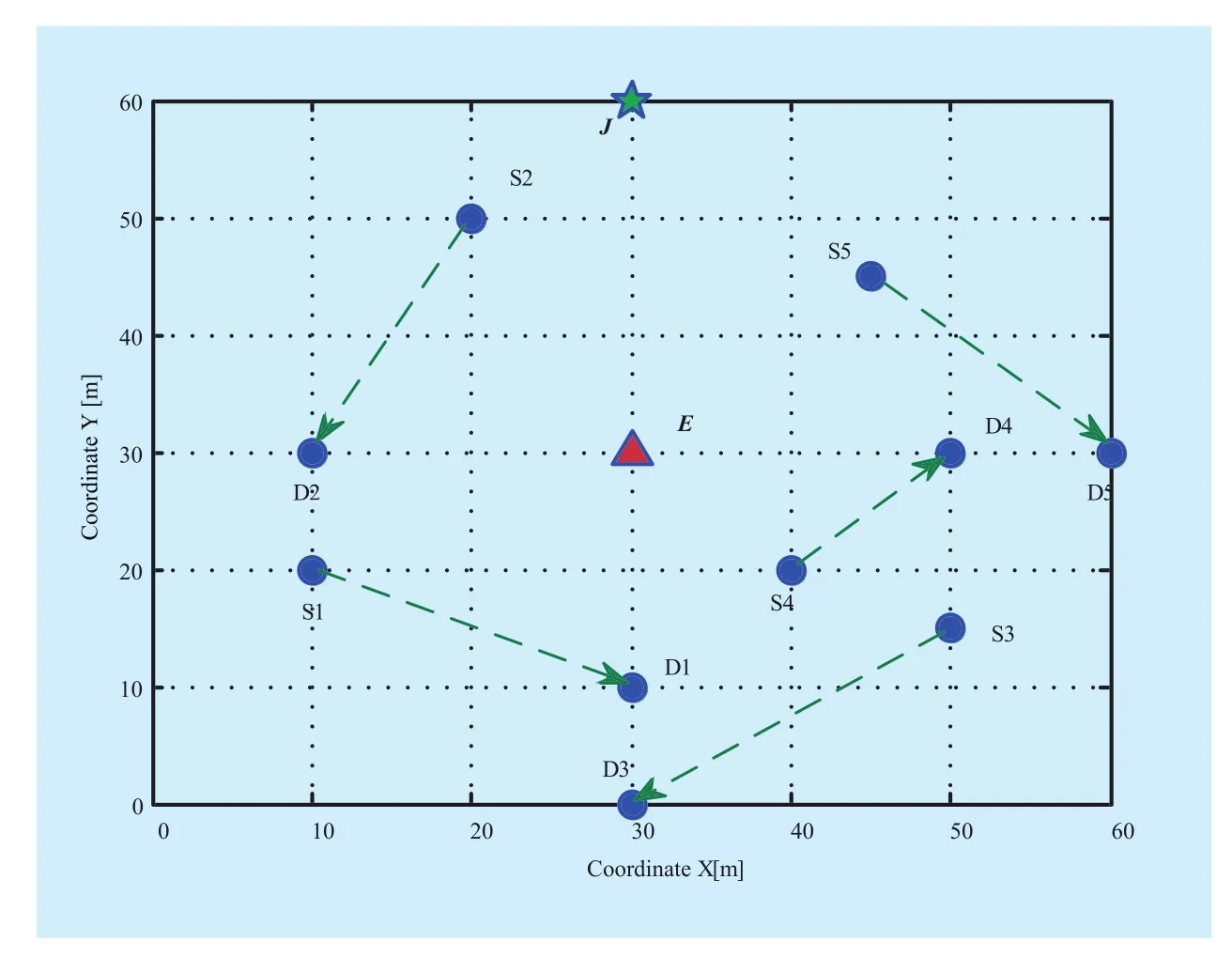
Fig. 2 A Simulation of the CRN with five PUs, a SU, and an eavesdropper

When maximum available jamming power decreases, the equilibrium strategies of both PUs will decreases, the competition between PUs will be enhanced. Each PU will have to grant more spectrum in exchange for the desired jamming power. The convergence of proposed Gauss-Jacobi iterative algorithm is shown in Fig. 4(b). From Fig. 4(b), we can observe that, at each iteration, the strategy selected by each PU is the best response strategy assuming its rival’s strategy is still the strategy at the previous iteration. Moreover, in our proposed scenario, the proposed algorithm may achieve convergence after several iterations.And the final result is same as the equilibrium point in Fig. 4(a). It means that when the algorithm convergence, the equilibrium result can be obtained through using our proposed algorithm. But it should be pointed out that the convergence of our algorithm cannot always be guaranteed.

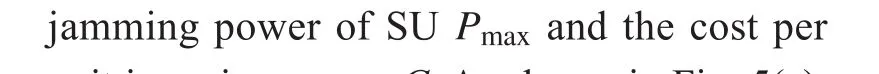
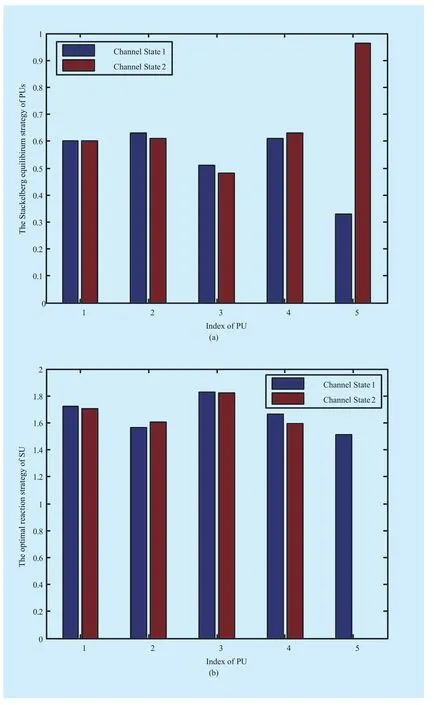
Fig. 3 The Stackelberg equilibrium results under different channel state. (a) The Stackelberg equilibrium strategy of each PU. (b) The optimal reaction strategy of SU

From Fig. 5(b), we can observe that with the cost of per unit jamming powerCincreases, the secrecy rate obtained by PU will decreases. This is because the rising cost will lead to the decrease of jamming power allo-cation for the same granted spectrum fraction.Fig. 6 shows that with the increase of the number of PU, the average secrecy rate obtained by PU decreases, but the utility achieved by SU increases. The reason is that with the increases of the number of PU, the competition between PUs will become more serious. In this case, each PU will grant more spectrum fraction to SU, but get less jamming power from SU. Therefore, the secrecy rate obtained by each PU will deceases. Moreover, according to the assumption, both of the secrecy rate obtained by PU and the utility of SU are equal to zero. However, as shown in Fig. 6, both of the secrecy capacity of PU and the utility of SU are greater than zero if the cooperation is built between PU and SU. It means that both PUs’ secrecy rate and SU’s utility can be improved through cooperation.

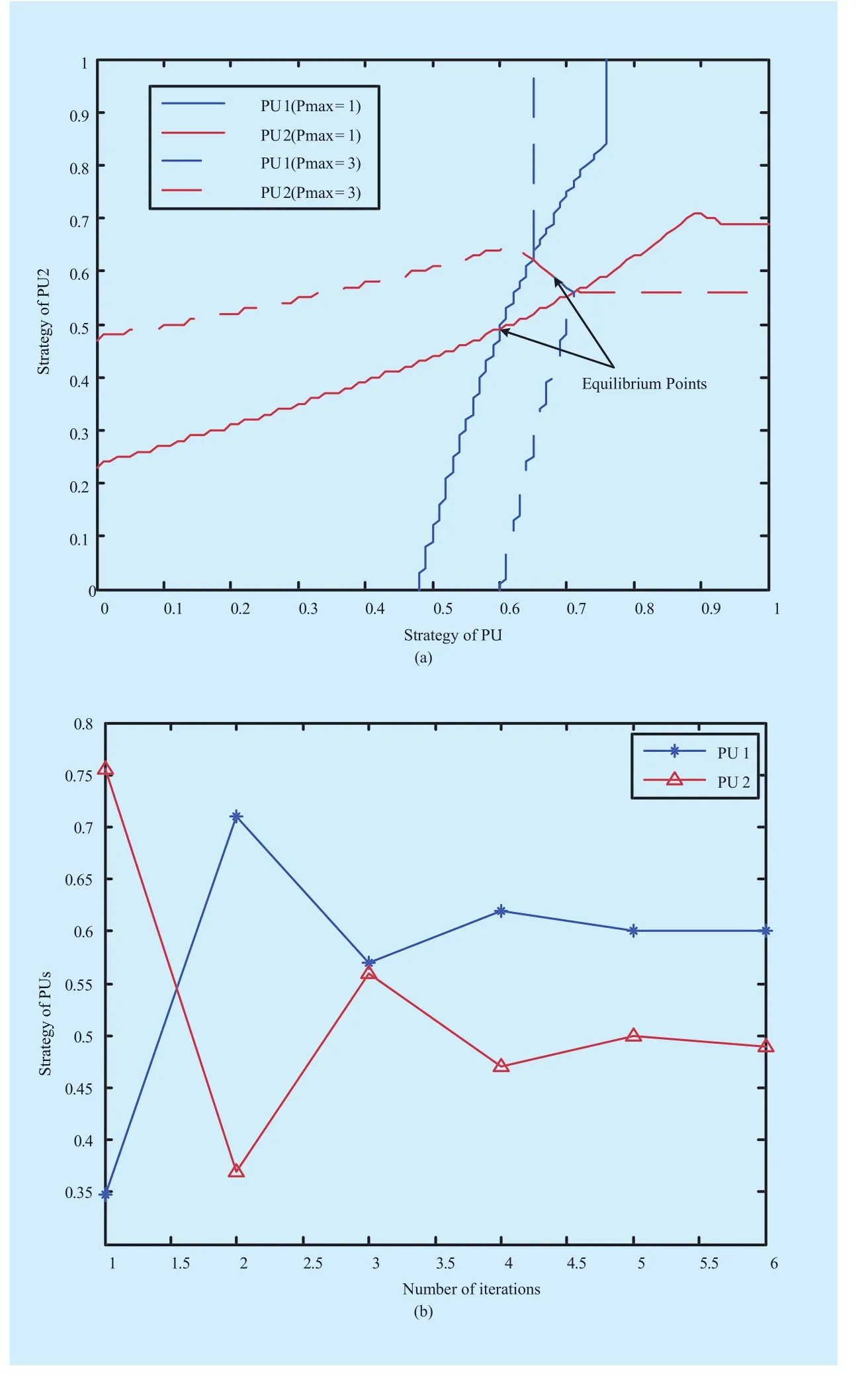
Fig. 4 The results obtained in the scenario only with PU1 and PU2. (a) Best response curve of both PUs. (b) Each PU’s best strategy in every iterations

V. CONCLUSION

In this paper, we have investigated the cooperative jamming between multiple PUs and single SU for secure transmission of CRNs.It focuses on such a cooperative jamming scenario in which, on the one hand, more than one PUs want to grant part of their spectral resources in exchange for friendly jamming provided by SU; on the other hand, SU might gain the transmission opportunity from multiple PUs through offering jamming service.A multi-leaders and single-follower Stackelberg game has been proposed to model the interaction between multiple PUs and single SU. Moreover, the competition among PUs is formulated as a GNEP, and the GNE is considered as the solution. If the proposed GNEP exists a GNE solution, then this GNE solution and its corresponding reaction strategy determined by SU constitute a Stackelberg equilibrium of the proposed Stackelberg game.Through analysis we obtained a meaningful conclusion, when the SINRs obtained by each PU’s destination node and eavesdropper node are much greater than one, the proposed Stackelberg game exists a Stackelberg equilibrium.Moreover, a Gauss-Jacobi iterative algorithm has been proposed to compute an equilibrium solution. Numerical results corroborate that both PUs’ secrecy rate and SU’s utility can be improved through cooperation, and the existing of competition among multiple PUs makes the Su gain more utility than without competition.

For future work, we will design a cooperative jamming scheme for the scenario with multiple PUs and multiple SUs. In addition,we will exploit the channel statistic information to make the proposed scheme more effi-cient. The effect of imperfect CSI on cooperation will be studied as well.

Appendix:Proof of Proposition 1

Proof： If Condition 1 satisfied, then the utility function of PUican be rewritten as follows

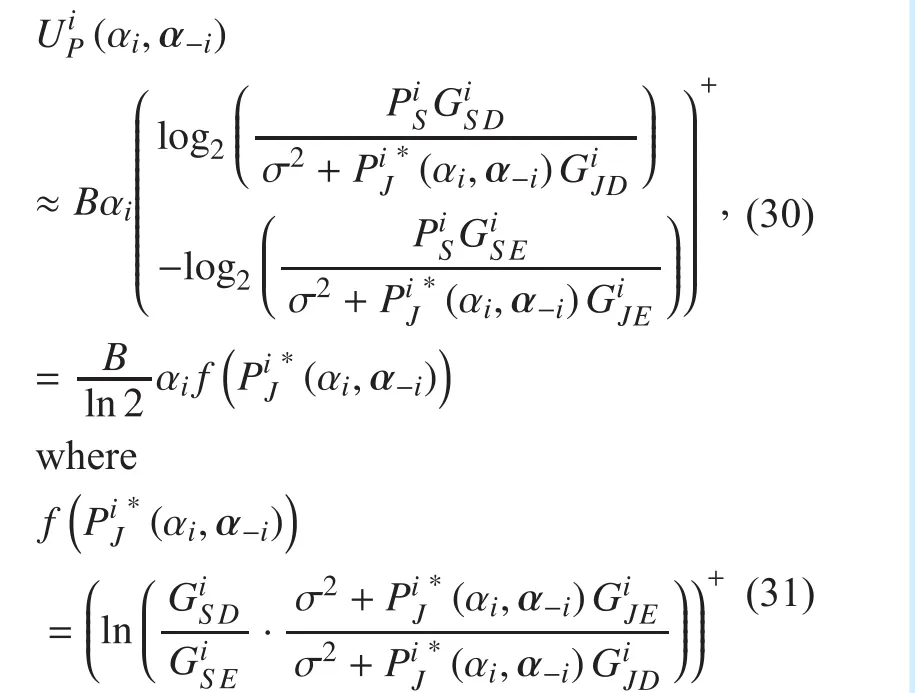
Now, taking the second-order derivatives of PU’s utility, we can get

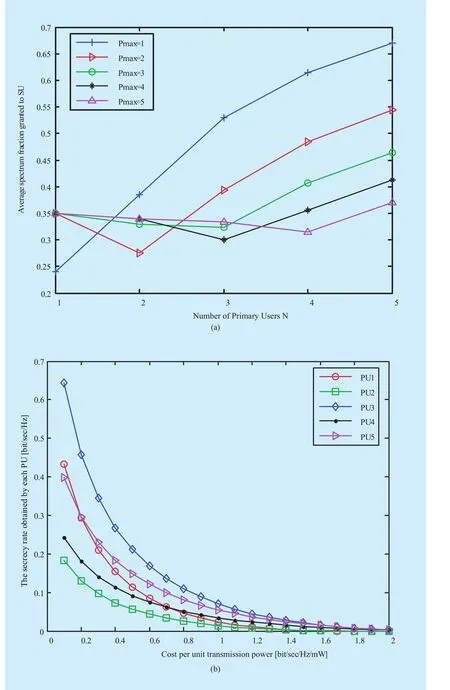
Fig. 5 The effect of different parameters on the final results. (a) The average granted spectrum fraction versus the number of PU and the maximum available jamming power. (b) The secrecy rate obtained by each PU versus the cost per unit jamming power of SU

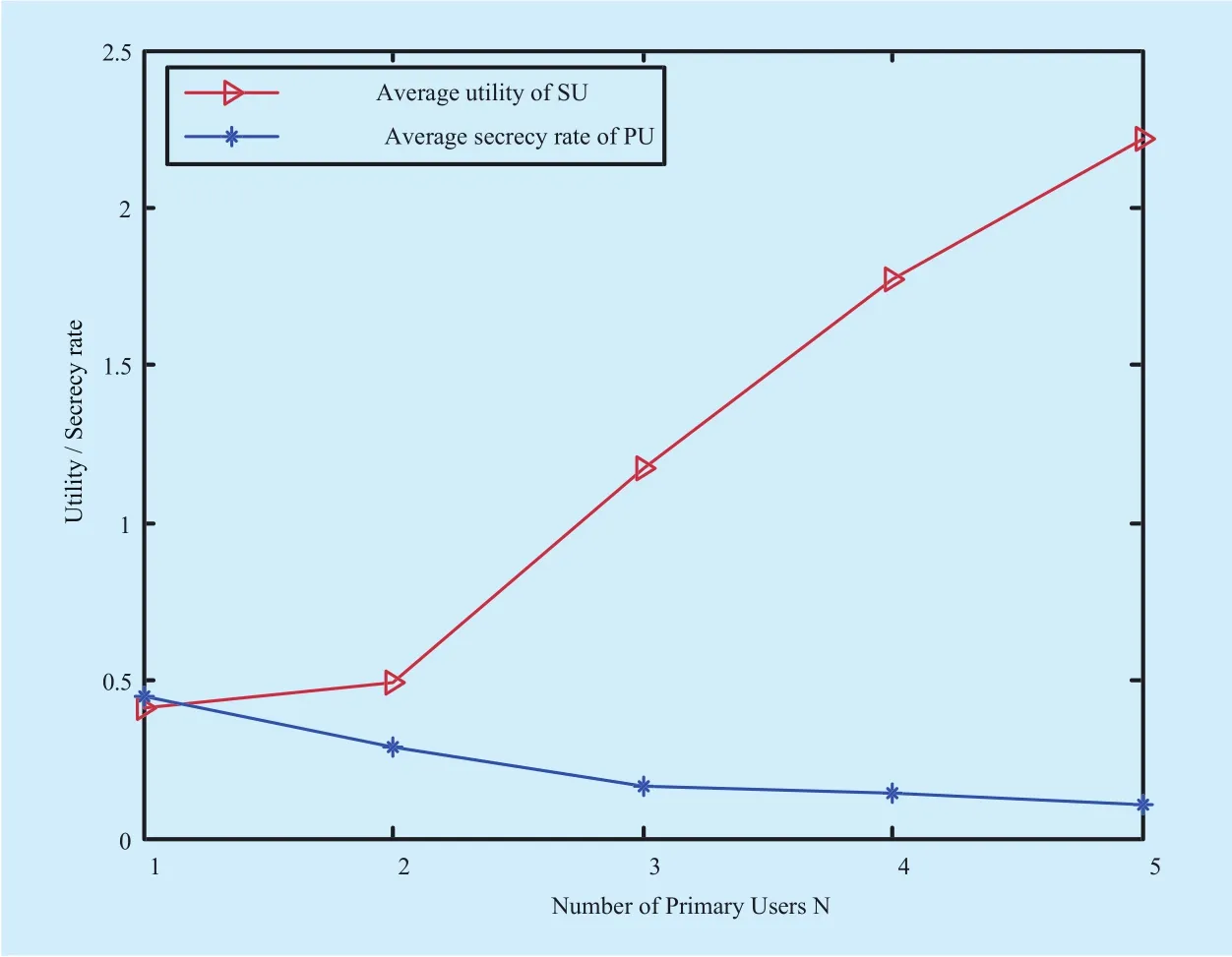
Fig. 6 The PU’s average secrecy rate and SU’s utility versus the number of PUs

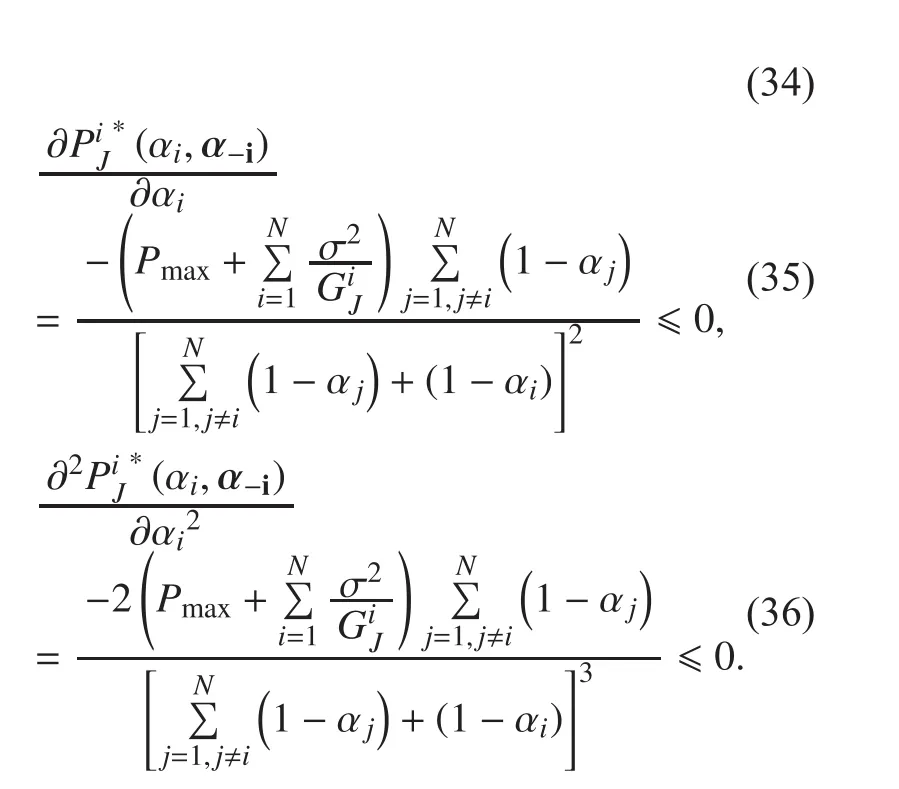
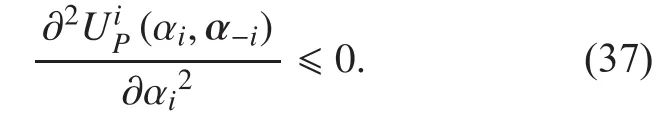
Therefore, if Condition 1 satisfied, for all

ACKNOWLEDGEMENTS

This work was supported in part by the National Key Research and Development Program of China under Grant 2016QY01W0204, in part by Key Industrial Innovation Chain in Industrial Domain under Grant 2016KTZDGY-02,and in part by National High-Level Talents Special Support Program of China under Grant CS31117200001.

[1] S. Haykin, “Cognitive radio: brain-empowered wireless communications.”IEEE journal on selected areas in communications, vol. 23, no. 2,pp. 201-220, February, 2005.

[2] B. Wang, K J R. Liu, “Advances in cognitive radio networks: A survey”,IEEE Journal of Selected Topics in Signal Processing, vol. 5, no. 1, pp.5-23, February, 2011.

[3] Q. Pei, B. Yuan, L. Li, et al. “A sensing and etiquette reputation-based trust management for centralized cognitive radio networks”,Neurocomputing, 2013, vol. 101, no. 3, pp. 129-138,February, 2013.

[4] A. Attar, H. Tang, A. V. Vasilakos, et al., “A Survey of Security Challenges in Cognitive Radio Networks: Solutions and Future Research Directions”,Proceedings of the IEEE, vol. 100, no. 12,pp. 3172-3186, December, 2012.

[5] M. Khasawneh, A. Agarwal, “A survey on security in Cognitive Radio networks”,IEEE 6th International Conference on Computer Science and Information Technology (CSIT), pp. 64-70,March, 2014.

[6] A. G. Fragkiadakis, E. Z. Tragos, I. G. Askoxylakis,“A Survey on Security Threats and Detection Techniques in Cognitive Radio Networks”.IEEE Communications Surveys & Tutorials, vol. 15,no. 1, pp. 428-445, First Quarter, 2013.

[7] Y. Liang, A. Somekh-Baruch, H. V. Poor, et al.,“Capacity of Cognitive Interference Channels With and Without Secrecy”,IEEE Transactions on Information Theory, vol. 55, no. 2, pp. 604-619,February, 2009.

[8] E. Silva, A. Dos Santos, L. C. P. Albini, et al.,“Identity-Based Key Management in Mobile Ad Hoc Networks: Techniques and Applications”.IEEE Wireless Communications, vol. 15, no. 5.pp. 46-52, October, 2008.

[9] A. D. Wyner, “The wire-tap channel”,Bell Labs Technical Journal, vol. 54, no. 8, pp. 1355-1387,October, 1975.

[10] Y. S. Shiu, S. Y. Chang, H. C. Wu, et al., “Physical layer security in wireless networks: A tutorial”,IEEE wireless Communications, vol. 18, no. 2, pp.66-74, April, 2011.

[11] S. Leung-Yan-Cheong, Hellman M E. “The Gaussian wire-tap channel”,IEEE Transactions on Information Theory, vol. 24, no. 4, pp. 451-456, January, 1978.

[12] J. Huang, A. L. Swindlehurst, “Robust Secure Transmission in MISO Channels Based on Worst-Case Optimization”,IEEE Transactions on Signal Processing, vol. 60, no. 4, pp. 1696-1707,December, 2011.

[13] I. Csiszar, J. Korner, “Broadcast channels with confidential messages”,IEEE Transactions on Information Theory, vol. 24, no. 3, pp. 339-348,May, 1978.

[14] L. Lai, H. El Gamal, “The Relay—Eavesdropper Channel: Cooperation for Secrecy”,IEEE Transactions on Information Theory, vol. 54, no. 9, pp.4005-4019, August, 2008.

[15] X. Tang, R. Liu, P. Spasojević, et al., “Interference Assisted Secret Communication”,IEEE Transactions on Information Theory, vol. 57, no. 5, pp.3153-3167, April, 2009.

[16] E. Tekin, A. Yener, “The General Gaussian Multiple-Access and Two-Way Wiretap Channels:Achievable Rates and Cooperative Jamming”,IEEE Transactions on Information Theory, vol. 54,no. 6, pp. 2735-2751, May, 2008.

[17] K. H. Park, T. Wang, M. S. Alouini, “On the Jamming Power Allocation for Secure Amplify-and-Forward Relaying via Cooperative Jamming”,IEEE Journal on Selected Areas in Communications, vol. 31, no. 9, pp. 1741-1750,August, 2013.

[18] J. Huang, A. L. Swindlehurst, “Cooperative Jamming for Secure Communications in MIMO Relay Networks”,IEEE Transactions on Signal Processing, vol. 59, no. 10, pp. 4871-4884, July,2011.

[19] Y. Liu, A. P. Petropulu, “Destination Assisted Cooperative Jamming for Wireless Physical-Layer Security”,IEEE Transactions on Information Forensics & Security, vol. 8, no. 4, pp. 682-694,February, 2013.

[20] A. G. Fragkiadakis, E. Z. Tragos, I. G. Askoxylakis,“A Survey on Security Threats and Detection Techniques in Cognitive Radio Networks”,IEEE Communications Surveys & Tutorials, vol. 15,no. 1, pp. 428-445, First Quarter, 2013.

[21] N. Zhang, N. Lu, N. Cheng, et al., “Cooperative Spectrum Access Towards Secure Information Transfer for CRNs”,IEEE Journal on Selected Areas in Communications, vol. 31, no. 11, pp.2453-2464, October, 2013.

[22] I. Stanojev, A. Yener, “Improving Secrecy Rate via Spectrum Leasing for Friendly Jamming”IEEE Transactions on Wireless Communications,vol. 12, no. 1, pp. 134-145, December, 2013.

[23] K. Lee, O. Simeone, C. B. Chae, et al., “Spectrum Leasing via Cooperation for Enhanced Physical-Layer Secrecy”,IEEE Transactions on Vehicular Technology, vol. 62, no. 9, pp. 1-5, June,2011.

[24] Y. Wu, K. J. R. Liu, “An Information Secrecy Game in Cognitive Radio Networks”,IEEE Transactions on Information Forensics & Security, vol. 6, no.3, pp. 831-842, April, 2011.

[25] S. Bayat, R. H. Y. Louie, Y. Li, et al., “Cognitive Radio Relay Networks with Multiple Primary and Secondary Users: Distributed Stable Matching Algorithms for Spectrum Access”,IEEE International Conference on Communications (ICC), pp.1-6, June, 2011.

[26] S. He, L. Jiang, C. He, “A novel secondary user assisted relay mechanism in cognitive radio networks with multiple primary users”,IEEE International Conference on Global Communications Conference (GLOBECOM), pp. 1254-1259December, 2012.

[27] S. K. Jayaweera, M. Bkassiny, K. A. Avery, “Asymmetric Cooperative Communications Based Spectrum Leasing via Auctions in Cognitive Radio Networks”,IEEE Transactions on Wireless Communications, vol. 10, no. 8, pp. 2716-2724,June, 2011.

[28] M. J. Osborne, A. Rubinstein, “A course in game theory”.MIT Press, 1994.

[29] S. Boyd, L. Vandenberghe, “Convex Optimization”,Cambridge University Press, 2004.

[30] F. Facchinei, C. Kanzow, “Generalized Nash Equilibrium Problems”,Annals of Operations Research, vol. 175, no. 1, pp. 177-211, March,2010.

[31] Z. Li, T. Jing, X. Cheng, et al., “Cooperative jamming for secure communications in MIMO Cooperative Cognitive Radio Networks”,IEEE International Conference on Communications(ICC), pp. 7609-7614, June, 2015.

[32] X. Wang, Y. Ji, H. Zhou, et al., “A Non-monetary QoS-aware Auction Framework towards Secure Communications for Cognitive Radio Networks”,IEEE Transactions on Vehicular Technology, vol. 65, no. 7, pp. 5611-5623, August, 2016.

[33] T. Chen, H. Q. Yuan, T. Z. Zhao, et al., “Joint beamforming and power allocation for secure communication in cognitive radio networks”,Iet Communications, vol. 10, no. 10, pp. 1156-1162,July, 2016.