同一法为勾股定理的推导提供解题生长点
潘薇羽��
【摘要】如何用解题式的思维方式去分析勾股定理的存在?教学中,若没有从教师提示的面积法分析直角三角形的三边关系,我们是否能让学生自己通过解题发现勾股定理,在这个过程中,教师需要做好怎样的方法铺垫,以帮助学生解题思维的顺利生长.
【关键词】同一法;勾股定理;解题思维生长点
1我怎么没想到
常见的勾股定理教学中,命题引入方式有两种:
(1)直接呈现式.有以下几种具体呈现形式:
①呈现毕达哥拉斯观察到的地板图案,请学生观察并提出问题:“你认为这三个正方形的面积之间存在着怎样的关系?”如图1;
②呈现以特殊数3,4,5为边长的直角三角形的三边正方形图,请学生算一算:“这三个正方形的面积之间存在着怎样的等量关系?”如图2;
③呈现弦图,请学生观察并分析其中几何图形的面積关系,如图3.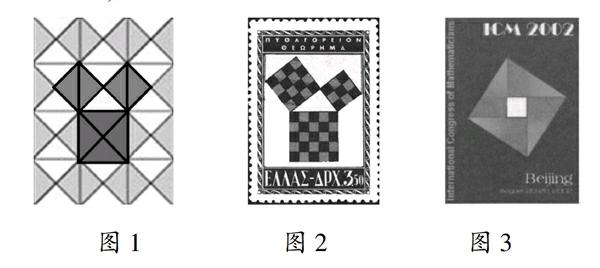
(2)问题发生式.此种教学法的常见形态有:
④测量猜想式.如:作两个直角三角形,使其两直角边分别是3cm和4cm,5cm和12cm,测一测斜边的长度;
⑤格点转移式.如:在网格中,作一个直角边长分别为3、4的直角三角形,量一量该直角三角形的斜边长是多少?若利用圆规,以斜边长为半径作弧,可发现圆弧经过另一个格点,数出半径长恰好是5个单位长度.同理,可以测量出直角边长分别为5、12的直角三角形的斜边长为13.
笔者初上讲台,使用直接呈现式的教学方式.每当展示勾股图的时候,笔者感受到学生的惊叹连连:“好聪明啊!”“他是怎么想到去算正方形面积的呢?”“我怎么就想不到呢?”“为什么会想到研究一个三边长为3、4、5的直角三角形?”虽然学生向笔者投来敬佩的目光,但似乎,疑问多于赞叹.
毕达哥拉斯从地板的图案上顿悟出勾股定理,是机缘巧合,但讲这样的故事就是学习数学了吗?
再次教学,笔者开始改用问题发生式教学,提出问题:你会求直角三角形的斜边长吗?笔者以为,用问题驱动的方式可以引导学生积极展开思维.而事实上,因为量一量的对象是特殊边长的直角三角形,结果也特殊,所以在量一量的环节,学生表现平静,无疑无赞.当笔者再接下来问:“这三个数据之间有什么特殊的关系吗?”学生的表现更是一愣一愣的,几分钟内,教室内只听见小小的嘀咕声,却没人说得出结果.当笔者再次点醒:“你没有发现32+42=52、52+122=132吗?”教室内顿时如炸开了锅一样,“原来是这样啊!”、“我怎么就没想到呢?”
一句话:“我怎么没有想到?”
——“我怎么没有想到以直角三角形的三条边为边构建正方形?”;
——“我怎么没有想到3、4、5之间、5、12、13之间会有什么相同的数量关系?”;
课后,学生问我:“老师,你是怎么想到的?你可以把你想到的方法告诉我吗?”
——“是啊,我是怎样想到的呢?前人是如何想到的呢?”笔者自问,并深深地思考:“毕达哥拉斯的顿悟虽是一种重要的解题方式,但学生对此的惊讶多于理解!是什么方法能让人想到这样的构图法解题?我该如何解题(求直角三角形的斜边长)、我该如何构图?”
2我该如何解题
再次执教这节课,笔者深深地思考:“如果没有勾股定理,我们应当如何求解直角三角形的斜边长?”
2.1从认知角度进行解题类别分析
求线段长度是常见的题型.一般在梳理问题条件时,需要从两个方向进行准备分析:一是问题条件的准备,二是知识准备.初中范围内,几何以三角形为基础,展开学习四边形、多边形、圆形,依据归纳转化的思想,当我们对知识系统中的上层知识进行学习、研究时,常常将其转化为对基础问题的求解,如求解多边形内角和时,将多边形转化为三角形进行求解;学习平行四边形的性质时,将四边形转化为三角形进行学习;解决不规则图形面积时,常常将不规则图形转化为规则图形进行处理.所以,对图形常见的处理方式是高级向低级的转化,不规则的图形向规则的图形进行转化,这是一种下位学习的方式,也是一种下位式的解题方式;奥苏伯尔曾在对认知结构进行分析的基础上,提出关于命题学习的三种分类:上位学习、下位学习、并列学习.通过命题学习,我们获得了命题的结论性知识,用命题的“结论解题”是数学解题中常常偏好的一个方向,只要能对问题的模式进行识别、会从命题的条件辨别异同,能在求同思维及求异思维的指导下进行分析,就可以解题.这是一种原型式的、特征式的解题方式.这种解题方式的缺点就是以结论为主,以原型模式辨别为主,很少在解题过程中明确解题的生长基础,并寻找解题的生长点.
借鉴奥苏伯尔的命题学习分类,我们也将解题学习分为三类:上位式解题、下位式解题、并列式解题.上位式解题:在解决问题时将问题向上一个层级的概念、命题进行转化,借助包容程度更高的命题、概念帮助解决问题;下位式解题:将问题向从属的概念、命题进行分解、转化,借助基础地、熟悉地、简易的知识结构解决问题,这也是一种常用的解题方式;并列式解题:在解决问题时,没有将问题的结构进行上位、下位概念命题的转移,利用同层级的概念、命题解题,比如:同一法证明勾股逆定理,文献[1]借助逆命题解题都是属于并列式解题的例子.
同一法在初中范围内应用不多,主要是因为用此法解题,不用调动上、下位的概念图式,对培养学生命题域的知识结构效用不大,所以在数学学习过程中,甚少出现,只是在涉及互逆命题的证明或使用互逆命题时,才被人记起,而这样的互逆命题教学,在初中的数学教学过程中,所占的比例仅仅微乎其微.
2.2同一法为勾股定理的推导提供解题生长点
近日,笔者在进行八年级《直角三角形的性质》教学时,频频接触到一组组互逆命题:①直角三角形斜边上的中线等于斜边的一半;如果三角形的一条边上的中线等于这条边的一半,那么这个三角形是直角三角形;②直角三角形中,30°的锐角所对的直角边等于斜边的一半;如果一个直角三角形中,有一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°.教学时,笔者着重对这些互逆命题的证明,及一些使用逆命题互助解题的例题进行重点教学,其间教授了同一法.而后又接触到勾股定理的教学.笔者在备课时以解题生长式的理念进行备课思考:如何求解直角三角形的斜边长呢?解决此命题的解题基础和解题生长点在何处?
解题基础分析:(1)关于勾股定理命题证明的条件只有一个:直角三角形;(2)与直角三角形边长有关的知识概念储备:无.
解题生长点分析:这样的命题解决,如何进行?解题的生长点在哪里?从条件分析,还是从储备知识分析?储备知识无,那么只能从条件入手,条件如何转化?此图中只有一个直角三角形,条件单一,如何转?转向何处去?
曾经学过的知识中,除三角形的三边关系,全等三角形的知识,其余者无.其中“三角形的三边关系”用不上,那么知识储备中就只有全等三角形的知识.“单木不成林”,单单一个三角形,哪来全等关系?可除了全等,还有何法?
不禁地,笔者想到才接触的同一法:是否可利用同一法将图形进行再建构?如果图中具有多个全等三角形,那么图形会变成……,尝试之后,笔者顿觉思路大开,原来,奥妙藏于此图中.笔者兴奋不已,借助同一法,进行了一堂非常顺利的勾股定理证明的教学课.以下为教学实录:
师:“前两节课我们用同一法解决了一些图形性質单一、不易于被证明的问题.同一法告诉我们:对于无法求解的线段,可在原图四周,重新建构一条长度相同的线段(或性质相关图形),通过证明新旧两图全等,而获得原线段长度.”
(呈现问题)……
师:“现在,我们如何求直角三角形的斜边AB的长?”
生:“我们可以在△ABC外再寻找长度等于AB的线段.利用圆规,分别以点A、B为圆心,AB长为半径作弧,圆弧经过格点E和F.因为线段BE、AF与线段AB一样,都是一个3×4的矩形对角线,所以AB=BE=AF,同理可证线段EF=AB.发现新组成的四边形ABEF是一个小正方形,被包含在大正方形CMNK中,可以证明小正方形四周均为全等的直角三角形.”
“这样的图形能帮助你求线段AB的长吗?”
“能.如果能算出正方形ABEF的面积,就可以知晓边长AB的值.”
“如何求小正方形ABEF的面积呢?”
此时,全班的声音异常整齐:“用大正方形的面积减去4个小直角三角形的面积!”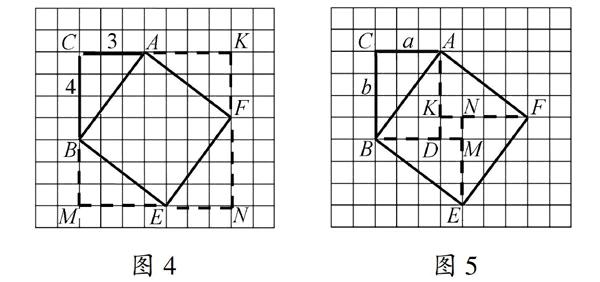
接下去的计算与推广证明过程便没有任何难度了.(图4、图5是两个学生的不同做法)
如何由一条线段想到构建四条边的正方形,如何由一个小直角三角形想到用4个全等的直角三角形进行拼图,思维的来源并不是空穴来风,重新构建,“同一法”证明给了我们极大的启示.图4图5
借助图4,证明勾股定理结论的过程为:设直角△ABC的两条直角边长为a、b,
易证四边形ABEF、CMNK为正方形.
因为S正方形CMNK=S正方形ABEF+4×S△ABC,
所以a+b2=AB2+4×12ab,
所以AB2=a2+b2.
即:c2=a2+b2.
证明至此,学生对于为何要构建正方形,为何要计算三个正方形面积之间的关系的理解便水到渠成了.
在此次证明中,正是因为证明的条件不多,图形不丰富,且曾经所学习的基础知识不够充分,所以只好选择同一法,通过构造一个与原图全等的图,并在丰富了图形之后,试图获取原图的图形性质.当我们构造一个全等的直角三角形之后,不妨再构造一些,进而获得了一个嵌入式的双正方形.利用小学的面积知识,便轻松地推导出勾股定理.此次解题证明初入时为并列式解题思路,后继发展为上位式解题方式,是初中数学中为数不多的上位式解题的典型题.
3思维的两种表现形式与教学方式
3.1直觉式顿悟与发生式学习
毕师关于勾股定理的发现是一种直觉式顿悟.“直觉是一种人们没有意识到的对信息的加工活动,是在潜意识中酝酿问题而后与显意识突然沟通,于是一下子得到了问题的答案,而对加工的具体过程,我们则没有意识到”[2].在顿悟之前毕师经过了观察,“观察是人们对事物的一个知觉过程.……知觉与人的经验分不开”,“直觉判断,个体利用自己的经验对知觉对象可能具有的属性作出一种判断”[3].毕师的发现是直觉式的,建立在他的经验之上,对着地板图案的观察,毕师能够将其中的图形结构进行重组分析,进而突显直至顿悟发现勾股定理.而对于初中学生,他们数学的直觉、数学经验、知识结构、数学方法尚不完善,虽说数学教学是要踩着历史的脚印前进,但要求十三、四岁的孩子们也能独自经历毕师的思维之路,困难程度不言而喻.
故而,勾股定理的认知,是否该是一种发生式的、过程式的学习方式呢?
发生式命题学习,是将命题产生的过程揭示出来,使学生在体悟命题发生和发展的认识中获得命题的学习方式[3].这种学习,也可以称为是一种过程性学习,从一个概念到另一个概念过渡的过程,方法的过程,推理的过程,获得思维的过程均在教学的范畴之中.概念固然是数学知识结构中的重要结点,但数学学习不仅仅是概念的习得,更重要的是如何在概念之间进行推理,使得概念点之间能够发生联结,这就是思维.数学是思维的体操,“数学是玩概念的”,数学要学习的,就是如何在概念之间产生往回地、多向地联结.所以,笔者认为勾股定理的教学中,三个正方形的面积计算不是主要的,如何想到构建正方形才是教学释疑的又一个重点.
3.2命题教学的结论性学习与生长式规则性学习
喻平认为,概念是数学的基础,数学命题由概念组合而成,在条件概念与结论概念之间,有“规则”连结,故命题学习也称规则学习[3].
笔者认为,规则是思维发生的过程与表现形式,思维的发生是有方向性、目的性的,是具有生长性的,因此,命题的规则性教学,应当从规则的生长性上进行考虑,包括生长点的分析与思考.其实,数学的学习就是规则性的学习,这是一种学习的方法论.规则具有自主的生长能力,解题时,思维在条件性概念与结论性概念之间进行各种方式地联结,若联结成功,则规则的生长成功.
对于教学而言,侧重结论式教学与侧重规则性教学,对学习者的思维培养效果有较大不同.若进行结论式教学,学习者的思维生长能力较弱;若进行发生式学习,在联结对象未知的情况下,思维的活跃程度相对更高,对解题者概念系、命题系的调动范围更大更积极,对思维能力的锻炼也就越高.所以,规则性学习是命题学习的一个重点内容,其价值高于结论性概念的获取.学习命题,不仅仅学习结论性知识,更有规则性内容.另外,命题教学的价值方向,就是提高解题能力,而解题教学的重点,是寻找具有生长基础(生长点)与生长方向的规则,进而培养思维的能力.
借助于同一法,笔者将“求解斜边长”的问题进一步扩大,进行上位式转化,进而顺利地解决了勾股定理的推导问题.既是教学思考必得,也是教学偶得,飨与读者.
参考文献
[1]陈明儒,岑霞丽.逆思补形分割[J].中学数学教学参考,2014,(4):38-39.
[2]钱学森.思维科学探索[M].太原:山西人民出版社,1985:22.
[3]喻平.数学教育心理学[M].南宁:广西教育出版社,2004:219.
作者简介潘薇羽(1978—),女,广西桂林人,中学高级教师,桂林市优秀数学教师,主要研究方向:生长式数学教学法.发表文章10余篇.

