基于SVR的股票价格预测研究
张柯柯
【摘 要】本文采用支持向量回归(SVR)对股票价格进行预测分析,以中国人寿(601628)为对象进行建模和预测研究。选取中国人寿2015-2016Q1的股票技术指标等数据作为训练样本对下一交易日的开盘价进行预测,以2016年4月的数据进行检验,并通过图像拟合来验证SVR用于股票预测的可行性和准确性。
【关键词】股票预测;支持向量机
1.引言
随着我国证券市场的深化发展,市场参与人数的增加,如何预测股票价格走势受到了广大投资者的关注。而股票市场的价格波动,一方面受IPO与资金的供求关系、大小非解禁和减持效应的影响;同时受宏观经济周期、货币供给、物价变化、利率水平等宏观经济因素和公司经营管理、治理结构等微观结构的影响;另一方面股票市场上投资者行为和政策性因素也会对股票市场波动产生重要影响。
为了保证投资收益降低风险,股票价格预测成为投资者关注的热点,同时股票市场的波动与货币政策、财政政策的变化密不可分,股票市场作为资本市场的重要组成部分,对推动经济的发展发挥重要作用,因而政策制定者也迫切需要了解宏观调控对股票市场的影响,预测股票价格波动。国内外学者们从不同角度,采用各种方法对股票价格做仿真实践与理论研究,如时间序列模型模型与神经网络模型。在时间序列预测模型方面,史书真(2013)[1]介绍了ARMA模型在股票预测中的应用,对中国石油等股票进行仿真,得出ARMA模型能较好的预测股价;徐枫(2006)[2]则用GARCH模型对我国航空业代表性股票进行仿真。在神经网络应用于股票预测方面:张健(1997)[3]研究了BP神经网络在股票价格预测中的应用,对“陆家嘴”等股票的样本数据进行学习和检验,得出BP神经网络在股票分析与预测中有一定的应用前景。陈政等人(2010)[4]利用RBF社交网络对生政综合指数进行仿真,得到了较好的预测效果。然而这些模型有其局限性,如存在局部极小值、欠学习、过学习等问题,SVM模型则较好的解决了上述问题,被广泛的应用于证券领域,并取得了很好的效果。
2.SVR
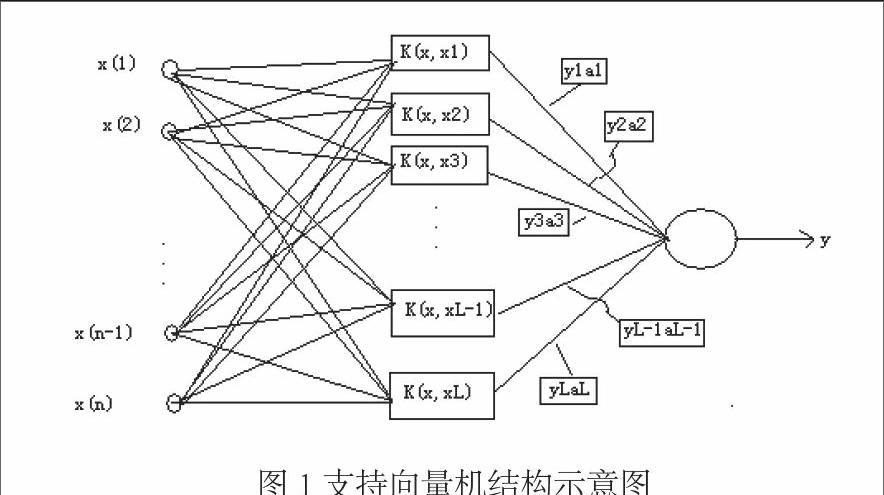
支持向量机(support vector machine, SVM)是美国Vapnik教授于1990年代提出的一种机器学习方法。SVM的基本思想是将原始非线性训练数据集通过非线性途径映射到一个高维特征空间,使其变得线性可分,然后在该特征空间中找到一个具有最大分离距离的超平面[5]。支持向量机的结构示意图可以表示如下:
支持向量机的网络结构类似于神经网络,其中输入层是为了存贮输入数据;中间层是通过对样本集的学习和选择;其输出则是若干中间层节点的线性组合。
支持向量回归(SVR)是支持向量在函数回归领域的应用。对于非线性SVR,其基本思想是通过将输入向量映射到高维特征空间中,然后在此高维空间中再进行线性回归,从而取得在原空间非线性回归的效果。使用支持向量回归(SVR)解决回归问题,首先应选择合适的核函数.常见的核函数包括线性核函数、多项式形式核函数、RBF(径向基)核函数、Sigmoid核函数等。本文选择式(1)所示的RBF(径向基函数)作为核函数.其次要选取合适的 RBF核参数、惩罚因子C和损失函数。 (1)
3.实验仿真
3.1 模型指标体系的构建
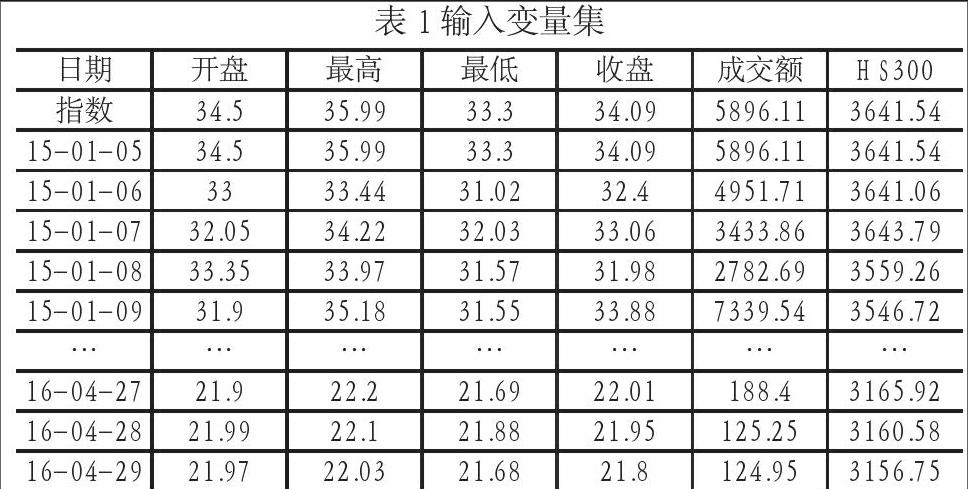
本文以上海证券交易所上市的中国人寿(601628)的股票数据进行预测,数据来源于WIND金融数据库。选取中国人寿(601628)2015年1月5日至2016年4月29日期间323个交易日的数据作为样本集,其中2016年4月份(后19個交易日)的数据作为预测样本,其余数据作为训练样本。以开盘价(元),最高价(元,最低价(元),收盘价(元),成交额(百万),沪深300指数作为股票价格预测的输入变量集,数据见表1所示;以下一日开盘价作为输出变量。
3.2 SVR参数选择
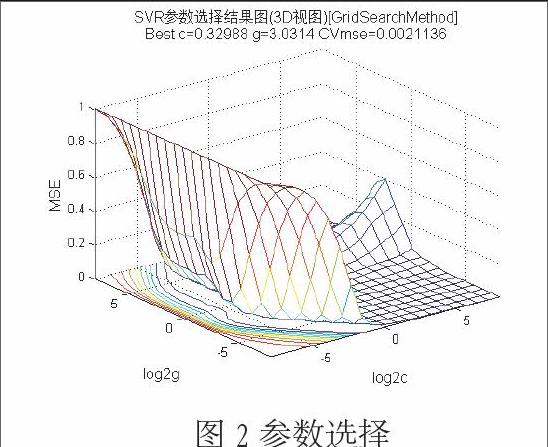
SVM的性能很大程度上依赖于核函数的选择,但没有很好的方法指导针对具体问题的核函数选择。SVMcgForRegress函数的目标是为SVM算法寻求一对最佳的参数c和g。
3.3实验结果分析
本文用SVR对中国人寿(601628)股票价格的预测结果如图3所示,从图中可见预测值与实际值的整体趋势基本符合实际数值的趋势。
从仿真的结果来看,可以看出SVR是可以对股票价格进行预测的,为投资者提供更好的投资依据,但在SVR核函数的选择及参数选定方面需进一步 研究。
参考文献:
[1]史书真.股价时间序列的分析与预测研究[D].大连:大连理工大学,2013.
[2]徐枫. 股票价格预测的GARCH模型[J].统计与决策, 2006(18):107-109.
[3]张健,陈勇,夏罡,何永保.人工神经网络之股票预测[J].计算机工程, 1997(2):52-55.
[4]陈政,杨天奇. 基于RBF神经网络的股票市场预测[J]. 计算机应用与软件, 2010, 27(06):108-110.
[5]钟用禄,李海山,刘发圣,谭鹏,张尚志,张成.基于PCA-SVR的燃煤锅炉NO_x排放预测[J]. 热力发电,2015(1):87-90.
[6]Vladimir Vapnik. The Nature of Statistical Learning Theory(Second Edition)[M]. Springer Verlag, 2000.

