最小可探测活度公式理解

潘竞舜

摘 要：最小可探测活度的正确理解与计算，对环境样品分析工作中低活度样品测量结果的正确判断非常重要。文章运用误差传递公式，对最小可探测活度的计算公式进行了推导。

关键词：本底计数率；误差；判断限；最小可探测活度

最小可探测活度是低活度样品分析测量中的基本概念，文献中[1-4]对最小可探测活度的计算，一般给出本底测量时间和样品测量时间相等时的计算公式。很少有文献给最小可探测活度表达的意义。根据误差传递公式，推导最小可探测活度的计算公式，可以帮助对最小可探测限的理解。

1 放射性测量的统计误差

放射性测量计数的统计误差和计数有联系，当计数足够大时，计数的标准方差σ2和计数的期望值M相等，σ2=M。在放射性测量过程中，用相同时间内对本底进行多次测量，测量结果是围绕某个平均值上下涨落。本底涨落由放射性衰变的随机性引起。本底计数率是一个随机数。测量放射性过程中，本底测量希望得到一个期望值（真值），本底计数率期望值需要无限多次测量，并计算平均值。在实验室测量中只能进行有限次数或单次测量。单次测量或有限次数测量不能得到真值。在本底计数次数足够大的时可以作为真平均值的近似。实际测量中本底计数是真值的近似值，本底计数率是有误差的。

在实际样品测量中，分析一个样品至少需要两个步骤，测量本底计数率和测量样品计数率。用nb、tb、ts分别表示本底计数率、本底测量时间、样品测量时间，根据误差传递公式可以得出本底产生的净计数率偏差 的计算式：

2 判断限

测量本底时的本底计数率和测量样品时的本底计数率都是统计计数率，因此两次本底计数率不一定相等（期望值是相等的）。这种本底的随机性涨落变化会影响样品净计数率的计算结果。由于本底的涨落产生的净计数率区间是（-∞，+∞），通常用LC（Critical Level）表示判断限，LC的值用下面的关系式表示：

式中kα表示概率分位值。

3 最小可探测活度

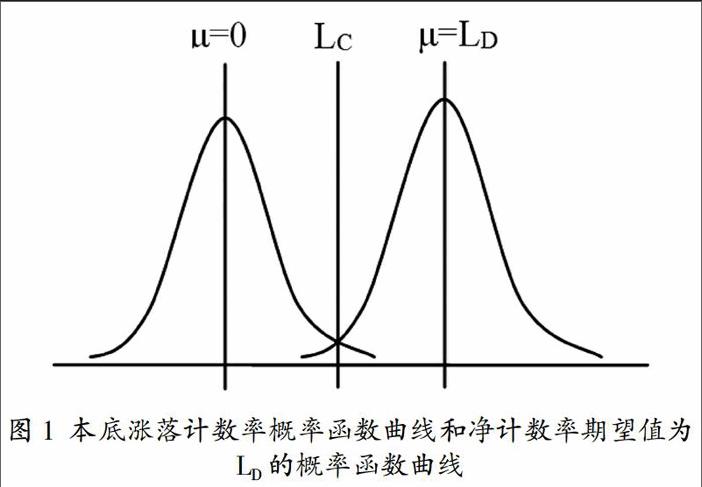
判断限对本底涨落的随机性统计做了考虑，放射性样品的衰变计数率也是统计计数，因此，对低放射性样品测量，考虑本底涨落的同时也要考虑净计数率的统计变化。假设仪器探测效率是100%，样品的活度是LD（LD>LC），本底涨落计数率概率函数曲线和净计数率（期望值为LD）的概率函数曲线如图1。交叉点对应的本底涨落计数率概率函数曲线分位值为kα，交叉点对应的净计数率（期望值为LD）概率函数曲线的分位值为kβ。

根据图1中本底涨落计数率、LD的概率函数曲线与期望值和偏差的关系，并用？滓L■表示LD的标准偏差。可以得出下面的关系式：

当kα=kβ，根据（2）、（3）式，解方程可以得到：

4 最小可探测活度

式（4）是通常没有考虑探测效率的LD计算公式。当kα=kβ=1.645时，置信水平为95%。在实际的环境低活度测量中，为得到足够的计数需要测量较长时间，因此式（4）中第一項的值很小，通常可忽略。考虑探测效率η，式（4）可表达为：

5 最小可探测限

最小可探测限的计算需要根据式（5）计算，计算过程中采用探测器自身的本底，还是试剂空白产生的本底，或其他因素产生的本底，要根据具体情况分析，同时还需要考虑样品参数，如样品重量、样品体积、回收率等。

6 结束语

在放射性测量中常用最小可探测限评判最小可探测限附近的测量数据，从而确定测量结果是否可以代表样品的放射性水平（由于置信度确定）。

在实际样品分析过程中，遇到低于最小探测限的数据通常注明低于最小探测限，对低于探测限的数据如何处理，相关文献[4]中做了详细说明。

参考文献

[1]郝润龙.低水平放射性测量中探测限的实用公式[J].计量学报，1983，4（4）：303.

[2]黄乃明.低水平放射性测量中的探测限及其计算[J].辐射防护通讯，2004，24（2）：25.

[3]周鹏，李冬梅，蒋跃进，等.海洋环境放射性监测的数据处理中存在的问题[J].海洋通报，2011，30（5）：544.

[4]沙连茂，卫为强，宣义仁.放射性环境监测中探测限附近测量数据的处理[J].环境监测管理与技术，2006，18（1）：38.