纵摇容器中液体晃荡的非线性数值模拟
宁德志,宋伟华,2,滕 斌
(1.大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024;2.中交第四航务工程勘察设计院有限公司,广州 510230)
纵摇容器中液体晃荡的非线性数值模拟
宁德志1,宋伟华1,2,滕 斌1
(1.大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024;2.中交第四航务工程勘察设计院有限公司,广州 510230)
在海洋工程领域,液体晃荡是一种普遍存在的物理现象。对于船舶而言,转动比平动有着更重要的影响。该文针对纵摇容器中的液体晃荡问题,采用高阶边界元方法建立自由水面满足完全非线性边界条件的时域数学模型。通过大地坐标系和随体坐标系之间的坐标变换,使得计算域仅控制在随体坐标系内。求解中采用半混合欧拉—拉格朗日方法追踪流体瞬时水面,运用四阶龙格库塔方法更新下一时间步的波面和速度势。通过与已发表试验和数值结果的对比,验证了建立模型的准确性。进而开展大量数值试验研究容器纵摇运动频率、纵摇转动中心和容器中布置一竖直隔板对晃动波面与荷载的影响。
液体晃荡;纵摇;完全非线性;高阶边界元;隔板
0 引 言
在海洋工程领域中,液体晃荡是一种普遍存在的物理现象。对于海上航行的船舶而言,纵摇运动对其稳定性的影响远远大于平动运动。尤其是当运动幅值很大或外界运动频率接近液舱的固有频率时,液体晃荡便会趋于剧烈,在内壁上产生极大的作用力,从而对结构造成危害,影响船舶的安全性和稳定性。
对于纵摇液舱中的液体晃荡,国内外许多学者已经进行了研究。Faltinsen[1]早在1974年就对二维矩形液舱作纵摇运动时的液体晃荡问题进行了非线性理论分析。此非线性理论解析解为后来学者进行数值模拟提供了很好的参照。Nakayama和Washizu[2]采用数值方法对二维矩形液舱纵摇运动的液体晃荡进行了模拟研究,他们利用有限元方法对空间进行网格划分,采用有限差分方法来计算时间递进。随后他们又运用边界元方法对二维纵摇矩形容器中的液体晃荡进行了研究[3]。同时,Chen[4-8]对于液舱纵摇运动的液体晃荡也做了大量工作。他针对理想流体的液体晃荡问题展开研究,分析了运动频率等因素的影响作用;同时还建立了粘性流模型,并将粘性流结果与理想流体结果进行对比分析。此外,他还针对复合运动液舱内的液体晃荡进行了研究,即液舱作平动和纵摇联合运动。
近几年来,Akyildiz和Unal[9-11]又针对矩形纵摇运动液舱中的液体晃荡进行了研究。他们分别采取了物理实验和数值模拟两种方法对液体晃荡产生的动水压强进行了研究对比,并且考虑了纵摇的频率和角度幅值对液体晃荡的影响。除此之外,Armenio[12]、Bae[13]、Celebi[14]和Xue[15]等学者也在这方面做了大量的研究工作。同时,国内学者肖龙飞等[16]、尹立中等[17]、洪亮等[18]、徐国徽等[19]也在这个领域有着较为深入的研究。然而,与平动运动液舱中液体晃荡的研究相比,人们对纵摇运动液舱中液体晃荡的研究还是相对较少,尤其是在减晃运动研究方面。
本文通过高阶边界元方法建立自由水面满足完全非线性边界条件的时域数学模型,针对液舱在不同转动中心和运动频率情况下的液体晃荡进行了数值试验,并分析了各因素的影响。在此基础上,考虑到对液体晃荡的抑制,本文还针对液舱中安置垂直隔板的情况进行了研究,给出了不同隔板位置、隔板长度情况下液体晃荡的波面幅值和液舱所受压力的变化趋势,可为实际工程提供一定的参考借鉴。
1 数学模型
1.1 控制方程和边界条件
如图1所示,一个长度为L、水深为H的矩形容器在外界激励作用下绕O点进行纵摇运动。定义两个笛卡尔坐标系:一个是固定大地坐标系O0X0Y0;另一个是运动的随体坐标系oxy。其中,x轴平行于容器静止时的自由水面且向右为正方向,y轴和容器的中心线重合且向上为正方向。当容器静止时,两个坐标系是重合的。同时,定义静止水面和x轴间的距离为e,且当x轴在静止水面以下时e值取为正。
假设流体是无粘、不可压缩且运动无旋的理想流体,则流体运动满足Laplace方程,

式中:φ表示速度势。
运动角速度ω()t定义为

式中:θ()
t表示液舱偏离静止位置的角度,且顺时针偏离为正值。

图1 示意图Fig.1 Definition sketch
同时假设:一是自由表面上的压强等于大气压强的自由表面边界条件;二是自由表面上的流体质点将始终保持在自由表面上。本文中将大气压强设定为0。基于第一条假设,自由表面的动力学边界条件可写为[2]
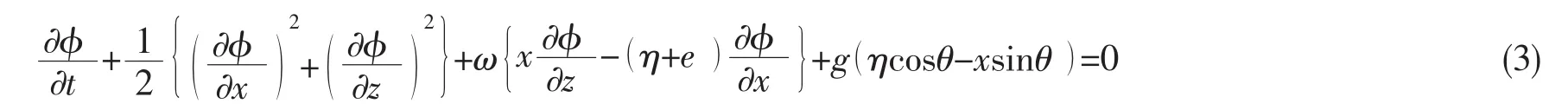
式中:η(x, )
t是自由表面偏离静止水面的位移,g是重力加速度。基于第二条假设,自由表面的运动学边界条件可写为[2]

式中:nx和ny是自由表面上的外法向量与x、y轴夹角的余弦值。∂/∂n表示在外法向上的偏导数。
在固壁上,边界条件可写为如下形式[2]:

当t=0时,容器静止不动,相应的初始条件可写为

此外,作用在液舱上的动水压力可由Bernoulli方程求得:
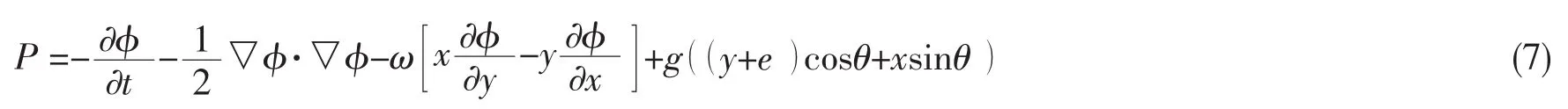
进而通过在容器瞬时湿表面上进行压强积分求出作用在容器上的荷载。
1.2 数值求解
为求解上节中的数学方程,在整个流域内对速度势应用格林第二定理,可得到如下边界积分方程[20]:

式中:p为源点,q为场点,C为固角系数,S为流域边界,包括自由水面边界和固体边界。本文用三节点高阶边界元离散计算边界成一些曲线单元,单元内任一点的几何坐标和速度势等物理量可以用形状函数插值得到,这与曲面单元内的做法是相同的。G是简单格林函数,可写为

式中:r1=,H为水深。
接下来,积分方程(8)经过三节点曲线高阶边界单元离散后,便可以通过求解线性方程组得到相关未知量的值。计算中认为当前时刻物面Sn上的速度势法向导数和自由水面Sf上的速度势是已知的,根据积分方程计算当前时刻物面Sn上的速度势和自由水面Sf上的速度势法向导数,然后应用四阶Runga-Kutta法,根据自由水面条件式(3)、(4)计算下一时刻的水质点位置和自由水面Sf上的速度势,再对自由水面重新划分网格,重新应用积分方程计算下一时刻物面上的速度势和自由水面上的速度势法向导数。这样计算周而复始,直到计算结束[21]。
2 模型验证
作为算例,首先考虑一个长度为0.9m、水深为0.6m的矩形容器,运动方程为θ=θ0cosωt。其中,θ0是角度幅值,ω是运动频率。选取θ0和ω为0.8度和5.5 rad/s。转动中心设定在静止水面上,即e=0。由运动方程可知,当t=0时,容器有一个0.8度的倾角。初始波面设为静止不动,即初始波面与轴也有一个0.8度的夹角。通过数值收敛性分析,选取时间步长和网格大小为t=0.01 s、△x=0.045m、△z=0.05m。图2给出了容器右侧壁处的波面时间历程图及本文数值结果与Nakayama和Washizu数值结果[2]的对比。由图可知,本文数值结果与Nakayama和Washizu的数值结果吻合得非常好,且波面变化趋于共振。
接下来考虑另一个算例,矩形容器长度L=0.92m、水深H=0.31m。运动方程为θ=θ0sinωt。其中,θ0是角度幅值,ω是运动频率。此例中,选取θ0和ω为8.0度和2.0 rad/s。转动中心设定在静止水面上,即e=0。初始波面是静止不动的。通过数值收敛性分析,选取时间步长和网格大小为t=0.01 s,△x=0.046m,△z=0.052m。图3给出了容器右侧壁处的波面时间历程图及本文数值结果与Akyildiz实验数据[11]、Akyildiz的CFD数值结果[11]的对比。由图可知,本文数值结果比Akyildiz的数值结果更接近实验数据。
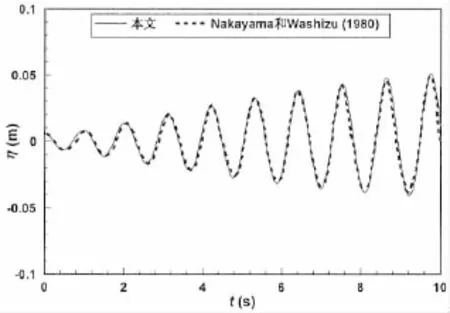
图2 余弦纵摇运动容器右侧壁处的波面时间历程Fig.2 Time series of surface elevation at the right wall subject to cosine pitch excitation

图3 正弦纵摇运动容器右侧壁处的波面时间历程Fig.3 Time series of surface elevation at the right end subject to sine pitch excitation
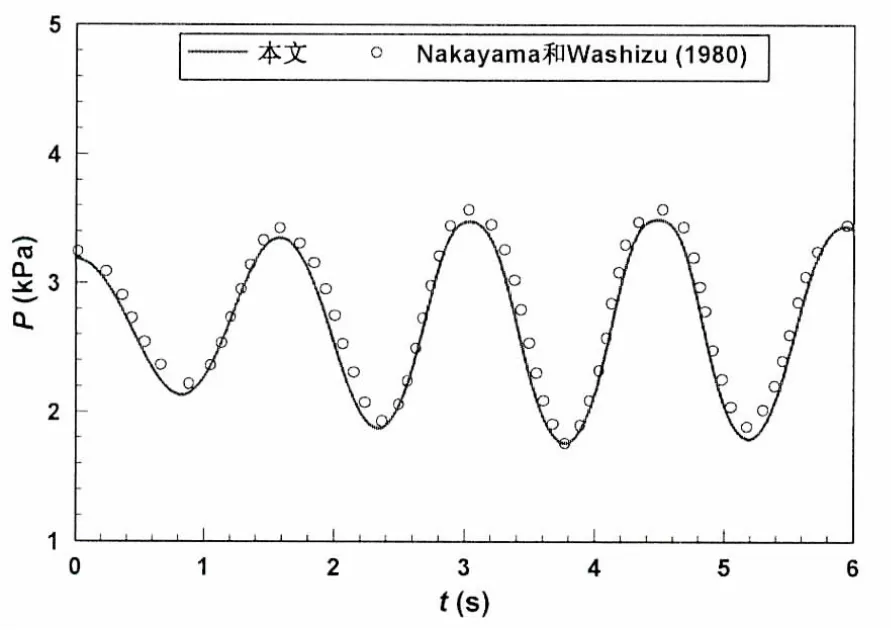
图4 右侧壁底部上0.075m处的压强时间历程Fig.4 Time series of pressure ata point0.075m from the rightwall-bottom
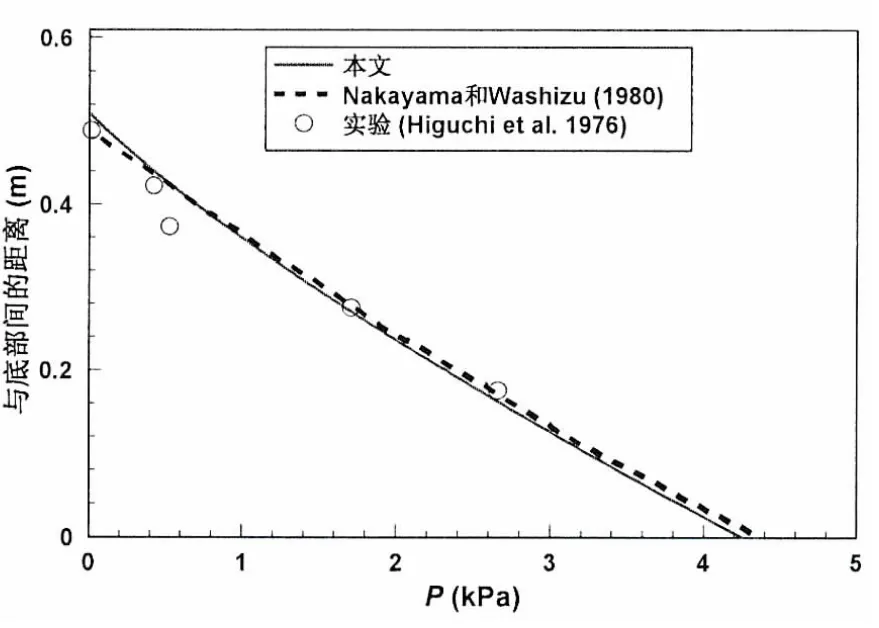
图5 t=5.52 s时右侧壁上的压强分布Fig.5 Distribution of pressure along the right wall at t=5.25 s
在上述波面验证的基础上,进一步开展数值模型的压强验证。选取容器长度L为1.0 m,水深H为0.35 m,运动方程为θ=θ0cosωt,θ0和ω为5.0度和5.19 rad/s。转动中心在静止水面以下0.1 m,即e=0.1m。图4给出了容器右侧壁上一点的压强时间历程图及本文数值结果与Nakayama和Washizu数值结果[3]的对比,这点距离液舱底0.075m。由图可知,本文数值结果与Nakayama和Washizu数值结果吻合良好。同时,图5给出了t=5.52 s时液舱右侧壁上的压强分布图及本文结果与Nakayama和Washizu数值结果[3]、Higuchi实验数据[22]的对比。由图可知,本文数值结果与Nakayama和Washizu数值结果吻合很好,与实验数据对比也吻合良好。
通过上述算例计算,验证了本文数值模型能够准确模拟纵摇容器中液体晃荡的波面变化和压强变化。
3 计算及分析
3.1 运动频率对液体晃荡的影响
众所周知,运动频率在很大程度上决定着液体晃荡的剧烈程度。当运动频率接近固有频率时,液体晃荡将会趋于共振,在结构上产生极大的压力。因此,本文将针对运动频率对液体晃荡的影响进行模拟研究。一般情况下,液体晃荡的强度主要通过波面幅值和作用在结构上的压力来反映。本文中,容器左侧壁处的波面幅值和作用在液舱上的水平力将被用来衡量液体晃荡强度。其中,水平力方向与x轴平行,且指向x轴正方向为正。为方便起见,本文统一规定:液舱尺寸L=1.0 m,H=0.5m,运动方程为θ=θ0sinωt,初始波面为静止水面。通过数值收敛性验证,时间步长和网格分别为△t=0.01 s和△x=△z= 0.05m。
对于L=1.0 m、H=0.5 m的矩形容器,其固有频率可由求得。其中,n表示固有频率的阶数。各阶固有频率分别为ω1=5.32 rad/s、ω2=7.84 rad/s、ω3=9.61 rad/s、ω4=11.10 rad/s、ω5=12.41 rad/s和ω6=13.60 rad/s。下面将针对运动频率是固有频率的情况进行模拟分析。选取了6个固有频率作为运动频率,分别为ω1、ω2、ω3、ω4、ω5和ω6。转角幅值统一为1.0度。转动中心固定在静止水面上,即e=0。
图6给出了6个运动频率下液舱左侧壁处波面时间历程图。在图6(a)、(c)、(e)中,波面幅值随着时间逐渐增大;同时,运动频率越大,波面幅值增长的速率越小,波面幅值与时间的线性关系愈不明显。在图6(b)、(d)、(f)中,波面幅值随着时间没有增大的趋势,而是保持在一个稳定的数值,亦即没有发生共振现象。因此,相对于偶数阶固有频率来说,液体晃荡对奇数阶固有频率更为敏感并且当运动频率是奇数阶固有频率时,频率越小,其对液体晃荡的影响越大,共振现象越明显。
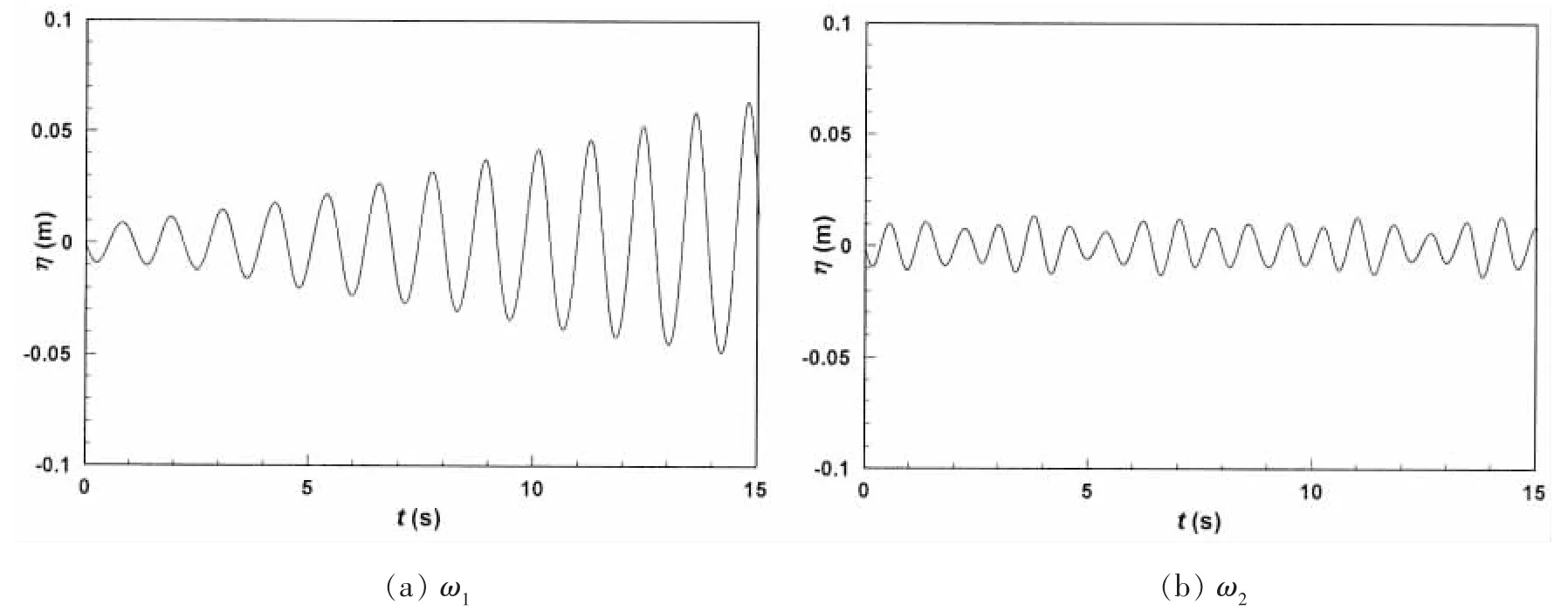
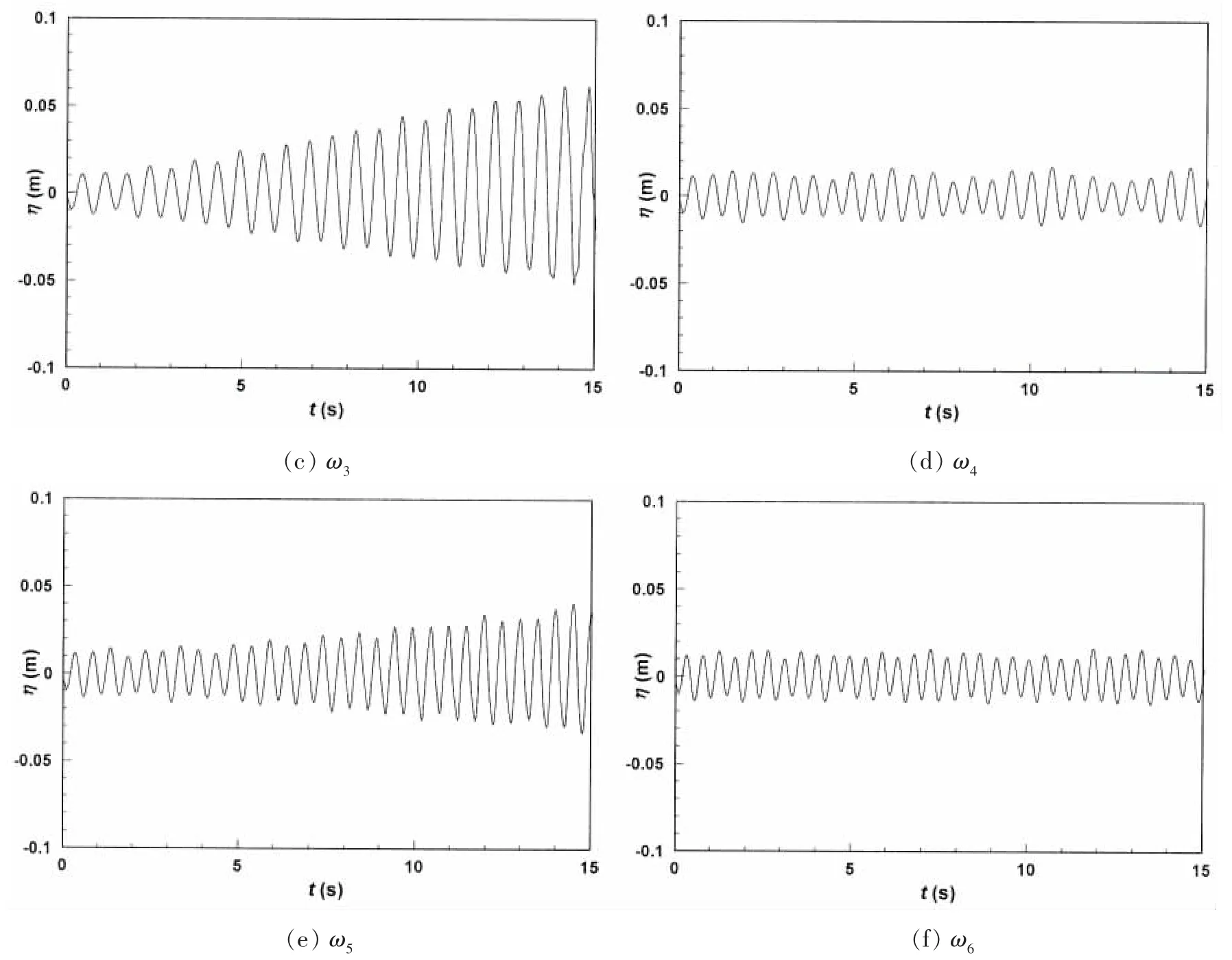
图6 不同运动频率情况下的容器左侧壁处波面时间历程Fig.6 Time series of surface elevation at the leftwall at differentexcitation frequency
3.2 转动中心对液体晃荡的影响
选定三种有代表性的转动中心位置e分别为-0.2 m、0、0.2 m。运动频率ω和转角幅值分别为ω1(容器的一阶固有频率为5.316 rad/s)和1.0度。
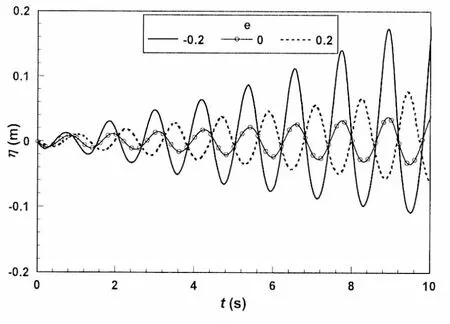
图7 容器左侧壁处的波面时间历程 Fig.7 Time series of surface elevation at the leftwall
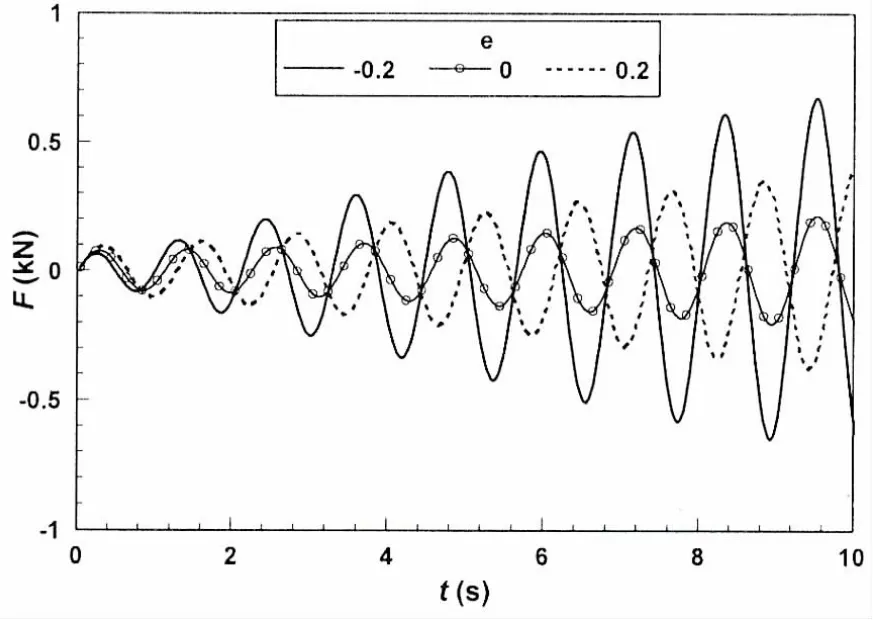
图8 作用在容器上的水平力时间历程Fig.8 Time series of horizontal force acted on the container
图7给出了三种情况下的容器左侧壁处波面时间历程。由图可知,当转动中心在静止水面(e=0)时,容器左侧壁处的波面幅值最小。当转动中心偏离静水面,转动中心在静止水面以上(e=-0.2m)情况下的容器左侧壁处的波面幅值要远远大于转动中心在静止水面下面(e=0.2m)情况下的。同时,图8给出了作用在容器上水平力的时间历程图。由图可知,转动中心在静止水面(e=0)时的水平力最小。当转动中心距离静止水面0.2m时,转动中心在静止水面以上(e=-0.2m)情况下的水平力要明显大于转动中心在静止水面下面(e=0.2m)情况下的,这同图7反映了同样的实质,即转动中心在静止水面以上更能激起容器中的液体晃荡。
3.3 隔板对液体晃荡的影响
对于在海上航行的液货船,纵摇是影响其内液体晃荡强度的重要因素。通常,人们在船舱内部加上不同形式的隔板来抑制液体的剧烈晃荡,从而保证船体的稳定性。本文中主要考虑垂直隔板对纵摇容器中液体晃荡的影响。考虑液舱具有一个长为0.3m、厚为0.01m的隔板。隔板是刚性的,固定在容器底部的左侧。隔板中心到容器中心的距离定义为D。运动频率ω为无隔板液舱的一阶固有频率ω1,转角幅值为1.0度。隔板上的网格大小为△x=0.01m和△z=0.02m。图9给出了隔板在不同位置D情况下左右侧壁处的最大波高值。由图可知,左侧壁处的波高值要大于右侧壁处的。两侧壁处的波高值都随着D的增大而逐渐增大。当隔板位置由0移动到0.3m时,波高值只增大很小的幅度。而当隔板位置由0.3m增大到0.4m时,波高值却急剧增大。图10给出了隔板在不同位置D情况下作用在液舱上的最大水平力。由图可知,最大水平力随着D的增大而逐渐增大。当隔板位置由0移动到0.3m时,最大水平力增大的幅值非常小。当隔板位置从0.3m增大到0.4m时,最大水平力却增幅明显。这与图9中波面值与D的关系是一致的。 因此,当隔板位置在区间(0,0.3L)内时,其位置对液体晃荡的影响不太明显。当隔板位置大于0.3L时,液体晃荡将对其位置将非常敏感。
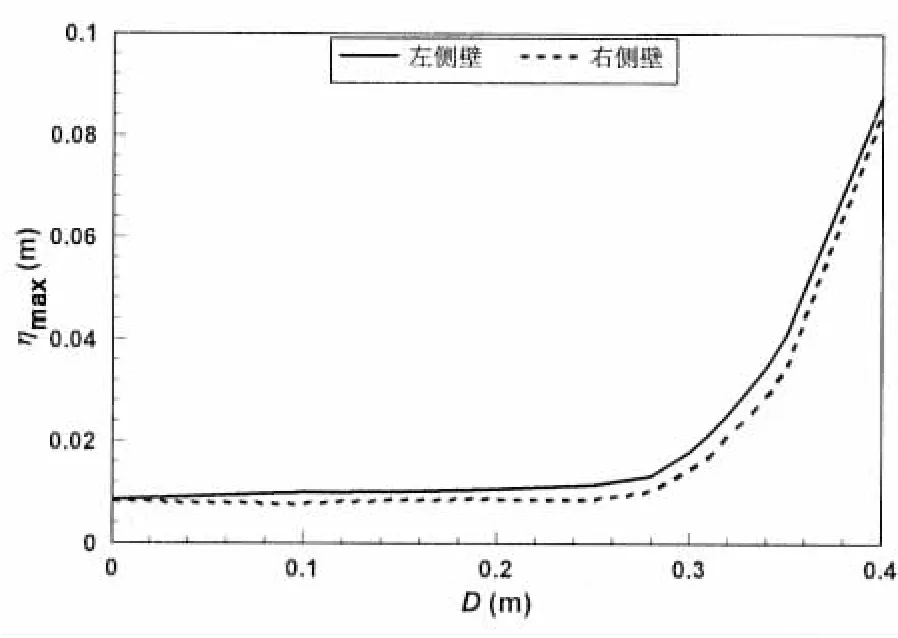
图9 不同D情况下的左右侧壁处最大波面高度Fig.9 Maximum surface-elevation at leftand rightwalls vs. distance between the baffle and bottom center
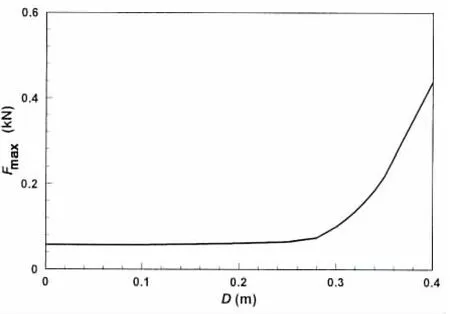
图10 不同D情况下的容器所受的最大水平力Fig.10 Maximum horizontal-loads on the container vs. distance between the baffle and bottom center
4 结 论
针对纵摇液舱中液体晃荡问题,本文利用高阶边界元方法建立模拟带有简晃隔板纵摇容器液体晃荡的完全非线性时域数学模型,通过坐标转换,使得计算域仅仅控制在随体坐标系内。通过纵摇容器中波面变化和作用在容器上荷载变化的模拟,并与已发表试验和数值结果的对比,验证了本文模型的准确性。进一步开展数值模拟研究发现,相对于容器的偶数阶固有频率来说,液体晃荡对奇数阶固有频率更为敏感,并且当运动频率是奇数阶固有频率时,频率越小,其对液体晃荡的影响越大;同时,转动中心在静水面以上容器中的液体晃荡效果更加显著,而转动中心在静水面上液体晃动效果最弱。此外,本文还研究了安置垂直隔板液舱中的液体晃荡。对于隔板长度一定的情况,隔板位置D在区间(0,0.3L)内时,其位置对液体晃荡的影响不太明显;当D大于0.3L时,液体晃荡将对其位置将非常敏感。
参 考 文 献:
[1]Faltisen OM.A nonlinear theory of sloshing in rectangular containers[J].Journal of Ship Research,1974,18:224-241.
[2]Nakayama T,Washizu K.Nonlinear analysis of liquid motion in a container subjected to forced pitching oscillation[J].International Journal for NumericalMethods in Engineering,1980,15:1207-1220.
[3]Nakayama T,Washizu K.The boundary elementmethod applied to the analysis of two-dimensional nonlinear sloshing problems[J].International Journal for NumericalMethods in Engineering,1981,17:1631-1646.
[4]Chen B F,Chiang H W.Complete 2D and fully nonlinear analysis of ideal fluid in containers[J].Journal of Engineering Mechanics,1999,125(1):70-78.
[5]Chen B F,Chiang HW.Complete two-dimensional analysis of sea-wave-induced fully non-linear sloshing fluid in a rigid floating container[J].Ocean Engineering,2000,27:953-977.
[6]Chen B F,Nokes R.Time-independent finite difference analysis of fully non-linear and viscous fluid sloshing in a rectangular container[J].Journal of Computational Physics,2005,209:47-81.
[7]Chen B F,Asce M.Viscous fluid in container under coupled surge,heave and pitchmotions[J].Journal ofWaterway, Port,Coastal and Ocean Engineering,2005,131(5):239-256.
[8]Chen B F,Wu CH.Effects of excitation angle and coupled heave-surge-swaymotion on fluid sloshing in a three-dimensional container[J].Journal ofMarine Science and Technology,2011,16:22-50.
[9]Akyildiz H,Unal E.Experimental investigation of pressure distribution on a rectangular container due to the liquid sloshing[J].Ocean Engineering,2005,32:1503-1516.
[10]Akildiz H,Unal E.Sloshing in a three-dimensional rectangular container:numerical simulation and experimental validation[J].Ocean Engineering,2006,33:2135-2149.
[11]Akildiz H.A numerical study of the effects of the vertical baffle on liquid sloshing in two-dimensional rectangular container[J].Journal of Sound and Vibration,2012,332:41-52.
[12]Armenio V,Rocca M L.On the analysis of sloshing ofwater in rectangular containers:numerical study and experimental validation[J].Ocean Engineering,1996,23(8):705-739.
[13]Bae H S,Yun YW,Park M K.Flow response ofmagnetic fluid surface by pitchingmotion[J].Journal of Mechanical Science and Technology,2010,24(2):583-592.
[14]Celebi M S,Akyildiz H.Nonlinearmodeling of liquid sloshing in amoving rectangular container[J].Ocean Engineering, 2002,29:1527-1553.
[15]Xue M A,Lin P Z.Numerical study of ring baffle effects on reducing violent liquid sloshing[J].Computers and Fluids, 2011,52:116-129.
[16]肖龙飞,杨建民,郭 彬.浅水FPSO垂荡和纵摇运动的低频响应[J].舰船科学技术,2009,31(11):120-125. Xiao L F,Yang JM,Guo B.Low frequency heave and pitch motions of FPSO in shallow water[J].Ship Science and Technology,2009,31(11):120-125.
[17]尹立中,邹经湘,王本利.俯仰运动圆柱贮箱中液体的非线性晃动[J].力学学报,2000,32(3):280-290. Yin L Z,Zou JX,Wang B L.Nonlinear sloshing of liquid in a circular cylindrical container under pitching excitation[J]. Chinese Journal of Theoretical and Applied Mechanics,2000,32(3):280-290.
[18]洪 亮,朱仁传,缪国平,范 菊.液舱晃荡对船舶横摇运动影响的数值研究[J].中国造船,2015,1:1-10. Hong L,Zhu R Z,Miu G P,Fan J.Numerical research on effectof sloshing on ship rollmotion[J].Shipbuilding of China, 2015,1:1-10.
[19]徐国徽,胡嘉骏,顾学康.耦合运动下液货舱晃荡压力预报研究[J].船舶力学,2016,20(7):884-891. Xu G H,Hu JJ,Gu X K.Prediction of sloshing pressure in coupledmotions for Liquid Cargo Carriers[J].Journal of Ship Mechanics,2016,20(7):884-891.
[20]李玉成,滕 斌.波浪对海上建筑物的作用(第2版)[M].北京:海洋出版社,2002. Li Y C,Teng B.Wave action onmarine structures(2nd Eidtion)[M].Beijing:Ocean Press,2002.
[21]宁德志.快速多极子边界元方法在完全非线性水波问题中的应用[D].大连:大连理工大学,2005. Ning D Z.Application of the fastmultiple boundary elementmethod to the fully nonlinear water wave problems[D].Dalian: Ph.D thesis,Dalian University of Technology,2005.
[22]HiguchiM,Tanaka T,Endo S.Study on hull vibration-induced container liquid sloshing in LPG containerers[R].Nippon Kokan Technology Report,1976,72:111-122.
Nonlinear numerical simulation of liquid sloshing in a container subjected to pitch excitation
NING DE-zhi1,SONGWei-hua1,2,TENG Bin1
(1.State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116024,China; 2.CCCC-FHDIEngineering Co.,Ltd.,Guangzhou 510230,China)
In the field ofmarine engineering,liquid sloshing is a kind of universal physical phenomenon. For the ship,the rotation has amore important influence than translation.Therefore,a time-domain numerical model is developed by higher-order boundary elementmethod to solve the liquid sloshing in a tank subjected to pitchmotion,in which the fully nonlinear boundary conditions satisfied on the free surface.With the coordinate exchanged between the global and local coordinates,the computational domain can be governed only in the local coordinates.In the solving process,a semi-mixed Eulerian-Lagrangian technique is applied to track the transient free surface and the 4th-order Runge-Kuttamethod is used to refresh wave elevation and velocity potential on the free surface at each time-step.The proposed numerical modelwas testified by comparison with the other published experimental and numerical results.On the base of validation,lots of numerical experiments are carried out to investigate the effect of pitch motion frequency,rotational center and a vertical bafflemounted on the container bottom on the sloshing surface and loads on the container.
liquid sloshing;pitchmotion;fully nonlinear;higher order boundary element;baffle
O353.2
:Adoi:10.3969/j.issn.1007-7294.2017.01.003
2016-09-01
国家自然科学基金资助项目(51679036,51490672);教育部新世纪优秀人才支持计划(NCET-13-0076)
宁德志(1975-),男,教授,博士生导师,E-mail:dzning@dlut.edu.cn;
宋伟华(1987-),男,工程师,E-mail:songweihua9@163.com。
1007-7294(2017)01-0015-08

