基于二次差分概率的无线信道估计方法

王立姣，杜薇薇，李凡，王智森

（大连工业大学信息科学与工程学院，辽宁 大连 116034）

基于二次差分概率的无线信道估计方法

王立姣，杜薇薇，李凡，王智森

（大连工业大学信息科学与工程学院，辽宁 大连 116034）

5G具有高速率和大带宽的特性，使得无线信号在时域和频域的衰落更加明显。随着差分值统计步长和空间采样间隔的增大，采用差分概率信道估计方法已无法跟踪深衰落区域，且峰值区域跟踪过度。针对以上问题提出一种二次差分概率的信道估计方法。该方法首先找到衰落曲线的谷值点和峰值点，然后通过二次差分概率对深衰落区域和峰值区域的估计差分值进行改善，最后利用差分运算得到估计增益。仿真实验结果表明，此方法有效地提高了整体的跟踪性能，并降低了跟踪误差。

5G；移动无线信道；信道估计；差分概率；二次差分

1 引言

信道是通信系统的重要组成部分，按照传输介质分为有线信道和无线信道，无线通信系统的性能在很大程度上取决于无线信道。关于无线信道模型，前人已经做了很多研究，了解信道模型的特征才能尽可能地提高有用信号在传输过程中的质量[1]。

20世纪60年代 ，Okumura测量了日本东京等地的无线信号传播特征，并做了一些统计图表得到Okumura模型[2,3]，此模型适用的小区半径范围为1～100 km。之后Hata在Okumura模型的基础上得到Okumura-Hata模型，该模型的小区半径为1～20 km，比Okumura模型缩小4倍[4,5]。但Okumura-Hata模型只适用于基站天线高度高于周围建筑物屋顶的情况。因此，科学和技术研究欧洲协会（EURO-COST）提出了 Okumura-Hata的扩展模型——COST231-Hata模型，该模型适用于基站密集区域，小区半径为0．5～20 km[6,7]。20世纪80年代末，Walfisch和Bertoni研发出 Walfisch-Bertoni模型，该模型的小区半径为0．2～5 km；随后，基于Walfisch-Bertoni模型和Ikegami模型，提出了COST231-WI模型，它的小区半径为0．02～5 km，但这两种模型均只适用于建筑物高度近似一致的城区和郊区[8-11]。现阶段常用的是基于LTE（long term evolution，长期演进）的3种模型，分别为EPA（extended pedestrian A model，扩展步行者信道模型）、EVA（extended vehicular A model，扩展车辆信道模型）和ETU（extended typical urban model，扩展典型城市信道模型），在市区环境中的小区覆盖半径一般都在1 km以内[12,13]。在5G通信系统中，信号传输速率有望达到 4G的6～10倍，小区半径会更小。

从以上信道模型总结得出，随着无线通信技术的发展，信号传输速率越来越快，无线信道模型的基站覆盖半径越来越小；同时由于传输速率的提高，使衰落对无线通信系统的影响越来越大。而在无线通信系统中由于空间的无限性，发射机和接收机之间的传播路径非常复杂[14,15]；地貌和天气等环境的影响使得无线信道具有极大的随机性。为了保证通信量，研究信道估计势在必行。

为了研究信道估计，需要熟知信道估计的传统方法。信道估计方法可以分为两类：一类是盲信道估计方法，另一类是基于导频的信道估计方法。盲信道估计方法不需要发送导频信号，频谱利用率高，但是接收机必须收到足够多的数据符号才可以保证可靠的信道估计，收敛速度慢、处理时延大、实现复杂度高。基于导频的信道估计的经典算法是最小二乘 （least square，LS）算法、最小均方误差（minimum mean square error，MMSE）算法和最大似然（maximum likelihood，ML）算法。LS算法是在发送端将已知的导频符号插入OFDM的特定子载波，在接收端提取特定位置导频，通过导频位置的信息来得到整个信道的信道响应，但是LS算法忽略了噪声的影响，当信道噪声较大时，信道估计的准确性下降[16]。MMSE算法考虑了噪声的影响，但是需要对矩阵求逆。当OFDM系统的子信道数目N较大时，矩阵运算量十分巨大，计算复杂度高[17]。ML算法检测时间短，且不需要知道信道的频率相关特性，但在信噪比较低的情况下，将噪声也检测为信号，去噪声能力不强[18]。在5G的研发过程中，我国提出了8个5G典型场景，包括密集住宅区、办公室、体育场和露天集会等，并包含地铁、快速路和高速铁路等中国特色场景及广域覆盖场景；并从场景使用性和技术重要性角度进行分析，将大规模天线阵列、超密集组网、全双工技术、新型非正交多址接入技术等列为5G的最核心技术[19,20]。其中，大规模有源天线阵列的基站侧可支持的协作天线数量将达到128根[21,22]，载波数量也随之增多；超密集组网是通过更加“密集化”的基站部署，缩小单个小区的覆盖范围，以获得更高的频率复用效率，但是随着小区部署密度的增加，超密集组网面临资源传输、部署成本等技术挑战[23]；非正交多址接入技术需要在接收端引入非线性检测来区分用户，能够依据多用户复用倍数成倍地提升系统容量，但同时也提高了系统的复杂度和部署成本[24]。不难看出，这些技术大大增加了信道估计的运算量。综上所述，必须找到一种新的信道估计方法来降低计算难度。

随着小区半径的逐渐缩小，电波在信道传播过程中经过的移动障碍物也随之变少。也就是说，距离衰减和遮挡衰减的概念逐渐被淡化，现阶段主要考虑的是多径环境中的信道模型。如图1所示，I区为距离衰减和遮挡衰减传播模型，Ⅱ区为多径区域传播模型。

图1 移动通信系统传播模型

本文针对Ⅱ区的信道特征，得到信道增益，分析发现信道增益具有时序性、可统计性且符合瑞利分布；信道增益之间的差分值又满足正态分布，因此结合信道增益及其差分值提出基于二次差分概率的无线信道估计。

2 移动无线信道基本模型

2.1 基本模型

移动无线信道的变化特征主要分为大尺度衰落和小尺度衰落。大尺度衰落描述了长距离内接收信号强度的缓慢变化，这些变化是由发射天线和接收天线间传播路径上的山坡、湖泊及一些大的建筑物等造成的。小尺度衰落主要是发射天线和接收天线之间的多径效应和多普勒频移作用的结果。在移动通信系统中，电波从基站发出，经历距离衰减、遮挡衰减到达移动终端附近后，由于移动终端周边的树木、建筑物、车辆等的散射、折射和反射，形成多路素波，这些素波在移动终端接收天线上叠加，形成快衰落的现象。如图1中的Ⅱ区，在这个很小范围内，距离衰减、遮挡衰减对接收电波的影响较小，故可以忽略不计，而素波叠加引起的多径衰落却非常大，因此，本文主要考虑多径衰落对信道估计带来的影响。

2.2 信道增益的数学表达

在无线信道中，由于基站与移动台的相对移动，信道具有很强的时变性，电波在移动信道传播过程中会产生多普勒频移。若移动台的移动速度为v，载波频率为fc，载波长为λc，第n路素波的到来方向与移动台的移动方向夹角为θn，满足θn=θ1+2π(n-1)/N，其中，θ1∈[0,2π/N]，N为电波由多径效应发生折射、反射产生的素波总个数，第n路素波的瞬时相位为n，其中，n∈[0,2π]。

如图2（a）所示，假设基站的位置为BS点，移动台以速度v在平面上由MS1点移动到MS2点。则第n路素波到达MS1点和MS2点之间的路程差就是基站BS和MS1点之间的距离与基站BS和MS2点之间的距离之差，由于远端距离很远，可假设MS1、MS2处的夹角相同，都为θn，那么路程差可表示为(h+h′)cos θn-h′cosθn，即：

其中，h为MS1、MS2两点之间的距离，h′为MS2、A两点之间的距离，A点为基站BS在移动台移动平面上的垂点，θn为素波到达MS1、MS2点后与移动方向的夹角。

在三维空间，如果无线信道中的物体处于静止不动状态，且运动只由移动台产生，则衰落只与空间路径有关[25]。如图2（b）所示，由于x轴和y轴正交，以地点（0，0）为基准点，根据式（1）可以推测出空间中第n路素波到达地点(x,y)的路径差为：

图2 多普勒效应

其中，x、y分别代表某一地点的横纵坐标位置，θn为第n路素波到达地点(x,y)点后与移动方向的夹角。

第n路素波到达地点(x,y)的相位变化为：

其中，λc为载波波长，θn为第n路素波到达地点(x,y)点后与移动方向的夹角。

因此，信道的复增益ξ(x,y)表示为：

其中，φn(x,y)为第n路素波到达地点(x,y)的相位变化，n为第n路素波的瞬时相位。由式（4）得知，移动台经过空间的不同点时产生的衰落不同。

2.3 信道增益分析

电波在无线信道传播过程中，由于受到移动台周边建筑物的遮挡、反射和折射，产生多径效应，变成多路素波（如图1的Ⅱ区），这些素波以极小的时间差到达接收端。因为这些素波的幅值和相位不同，在接收天线上进行幅值和相位叠加后，使得某一时刻的接收信号功率加强，某一时刻的接收信号功率减弱，形成严重的衰落，因此要进行信道估计。

本文对仿真实验所需的参数定义如下：增益，无线通信系统中接收机接收到的幅值，本研究取对数形式，单位为dB；差分值，某一时刻增益和下一时刻增益之差与空间采样间隔的比值，单位为dB/cm；空间采样间隔，空间衰落的抽样间隔，单位为cm；增益统计步长，统计信道增益特征的子区间长度，单位为dB；差分值统计步长，统计差分值特征的子区间长度，单位为dB/cm。

根据式（4）编写空间衰落仿真器，并设定仿真条件为：素波个数为16，空间采样间隔为1 cm，载波频率分别为2 GHz、5 GHz。得到的移动信道空间衰落如图3所示，对比图3（a）、图3（b）得出：相同物理条件下，载波频率越高，衰落变化越剧烈。

图3 移动无线信道空间衰落示意

为了更清晰地观察衰落变化的情况，将图（3）中连续的100个数据点展开，得到图4。其中，x=12，y= [1,2,…,100]，N=16，空间采样间隔为 1 cm。将这些采样点以 5 dB的等幅间隔分区间进行统计，可以看出落入深衰落点的增益个数明显减小，即落入深衰落的增益概率减小。

图4 采样示意

图5是在N=16、fc=5 GHz、空间采样间隔为1 cm的条件下，以不同采样点个数、不同增益统计步长得到的增益统计特征，发现增益服从瑞利分布。

对图5中的增益进行差分运算，得到差分值的统计特征如图6所示，可以看出差分值服从正态分布。

3 基于差分概率估计方法叙述

3.1 分析

观察图3～图6可以得到以下结论。

· 在相同物理环境下，载波频率越高，衰落速度越快，即增益间的差分值越大。

· 各采样点之间具有时序相关性，时序值点Ai+1与时序值Ai点、Ai-1以及二者的差分值正负相关。

·曲线有峰值点和谷值点，将100个增益采样点以5 dB等幅间隔分区间统计，可以看出，随着衰落深度的增加，落入深衰落的增益概率减小。

· 衰落可统计，且对整体而言符合瑞利分布。

·各时序点的差分概率分布是存在的，符合正态分布N(μ,σ)(μ≠0)，差分值接近零时的概率最大。

图5 增益统计特征

·增益及其差分值概率的大小与各自的统计步长、采样点个数有关；统计步长相等，采样点个数越大，精度越高；但当采样点个数相同时，统计步长越小，精度不一定越高。精度的指标可用均方差表示。

·采样点个数相同，统计步长为n倍关系，所得增益和差分值的期望或均方差也近似成n倍关系。

由以上分析可得出结论：衰落可统计，且符合瑞利分布；增益差分值概率符合正态分布。

图6 差分值统计特征

根据上述结论，引用基于差分概率的信道衰落估计方法。首先对各时序点的差分值进行概率统计，然后求出下一时刻的估计差分值，最后利用差分概率的思想得到估计增益。

3.2 方法叙述

条件1 接收信号的前两个采样点增益A1、A2及第一个差分值k1已知。

条件2 采样点总个数为m，空间采样间隔为Δ，差分值统计步长为Δk，最小差分值和最大差分值分别为mink、maxk。

条件 3 以相等 Δk划分差分值区间[mink,maxk]，得到的差分值子区间总个数t=(mink、-maxk)/Δk，其中，t向上取整数。落入每个子区间的差分值个数为nr(r=1,2,…,t)。

步骤1 根据式（4）编写空间衰落仿真器，得到信道增益。

步骤2 对接收信号的增益Ai进行差分运算，得到其差分值。

其中，i=1,2,…,m-1，Ai为当前时刻的增益值，Ai+1为下一时刻的增益值，ki为当前时刻的差分值，Δ为空间采样间隔。

步骤 3 以相等 Δk划分差分值区间[mink,maxk]，得到的差分值子区间分别为[mink,mink+Δk]，[mink+Δk,mink+2Δk]，…，[mink+wΔk,mink+(w+1)Δk]。其中，w=0,1,…,t-1，i=1,2,…,m-1，Δk为差分值统计步长。

步骤 4 找到落在某个子区间内差分值的下一时刻的所有差分值kp，对这些差分值求平均值，所得结果作为该子区间下一时刻的估计差分值，即：

其中，nr为落入每个子区间的差分值个数，p=1,2,…,nr，r=1,2,…,t。

步骤5 判断差分值ki-1所属区间，并将对应区间的^kr作为下一时刻的估计差分值，即：

其中，^kr为某一子区间下一时刻的估计差分值，r= 1,2,…,t，i,=1,2,…,m-1。

步骤6 通过差分计算求出估计增益值，为：

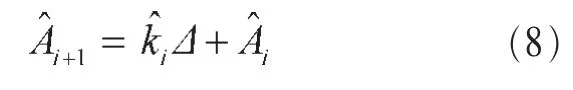
其中，^Ai当前时刻估计增益值，^Ai+1为下一时刻估计增益值，^ki为当前时刻估计差分值，Δ为空间采样间隔。

3.3 仿真性能评估

信道估计的精确度可以用真实值与估计值之间误差的均方差σ表示。将真实增益值记为Ai，估计增益值记为^Ai，估计值偏离真实值的距离即误差为：

误差均值为：

则误差均方差为：

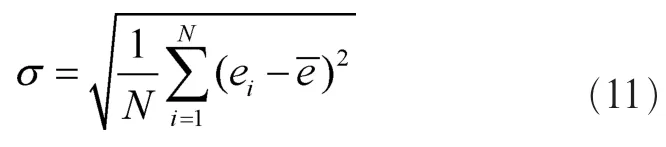
均方差的值越小，说明信道估计的性能越好。

4 仿真实验

本实验中主要考虑N=16，fc=5 GHz条件下，参数Δk和Δ对信道估计方法的影响。确定采样点的长度不变，则采样点的个数与空间采样间隔Δ成反比，其中，Δ的取值与载波波长 λc有关。

4.1 最佳集合长度

为了使增益和差分值的统计特征最接近瑞利分布和正态分布，需要找到最合适的实验点总个数进行仿真，即最佳集合长度。实验条件为N=16，fc=5 GHz，Δk=0.1 dB/cm。其中，m为采样点总个数，μ为期望，σ为均方差。

当Δ=0.1λc时，不同集合长度的增益、差分值参数对比见表1、表2，当集合长度达到100万及以上时，期望和均方差变化是由十万分位上变动引起的，影响非常小，可忽略不计。因此当Δ=0.1λc时得到的最佳集合长度为100万。

表1 Δ=0.1λc时增益参数对比（单位：dB）

当Δ=0.05λc时，不同集合长度的增益、差分值参数对比见表3、表4，当集合长度达到100万及以上时，得到的期望和均方差的变化是由万分位上的变动引起的，影响非常小，可忽略不计。因此当Δ=0.05λc时得到的最佳集合长度为100万。

当Δ=0.02λc时，不同集合长度的增益、差分值参数对比见表5、表6，当集合长度达到100万及以上时，期望和均方差的变化是由万分位上的变动引起的，影响非常小，可忽略不计。因此当Δ=0.02λc时得到的最佳集合长度为100万。

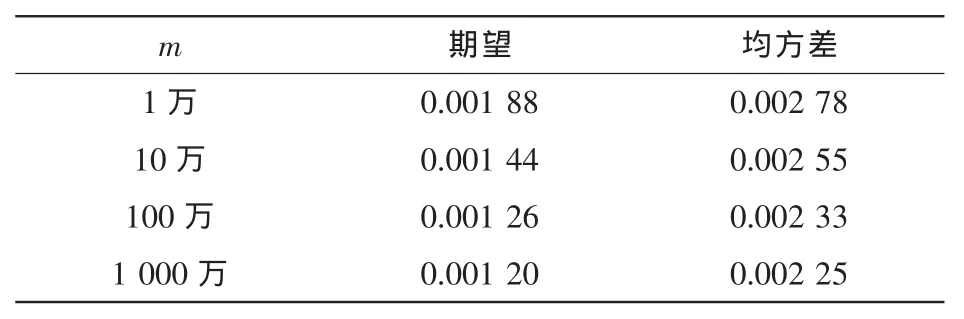
表3 Δ=0.05λc时增益参数对比（单位：dB）

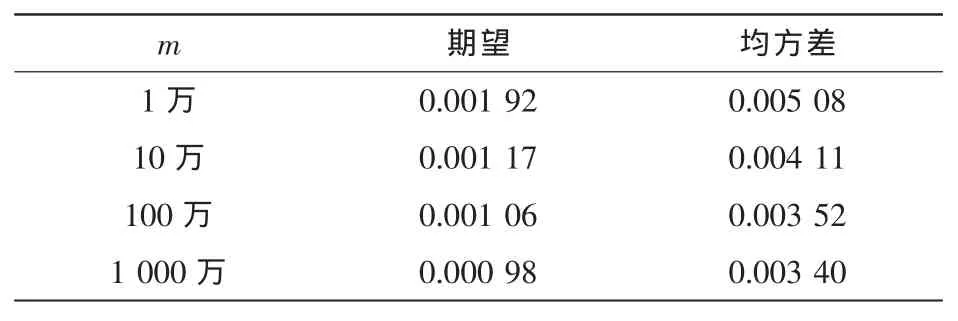
表4 Δ=0.05λc差分值参数对比（单位：dB/cm）

表5 Δ=0.02λc时增益参数对比（单位：dB）

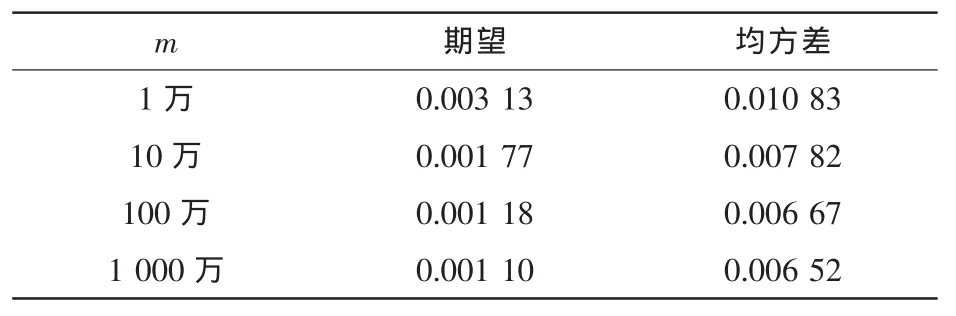
表6 Δ=0.02λc差分值参数对比（单位：dB/cm）

当Δ=0．01λc时，不同集合长度的增益、差分值参数对比见表7、表8，当集合长度达到100万及以上时，得到的期望和均方差的变化是由万分位上的变动引起的，影响非常小，可忽略不计。因此当Δ=0．01λc时得到的最佳集合长度为100万。

表7 Δ=0.01λc时增益参数对比（单位：dB）

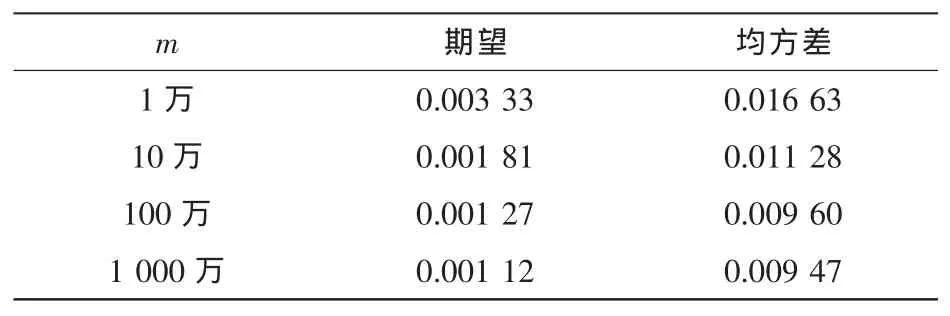
表8 Δ=0.01λc差分值参数对比（单位：dB/cm）

4.2 Δk的影响

4．2 ．1 仿真实验参数

Δk不同其他条件相同仿真实验参数见表9。

表9 Δk不同的仿真实验参数

4．2 ．2 仿真实验分析

Δk不同得到的仿真实验结果如图7所示，其中，m= 100万，Δ=0．1 λc，为便于观察，将真实值与估计值选择连续的150个采样点在平面图形中展开，分析发现：相同物理条件下，随着Δk的增大，均方差变化非常小；Δk成倍数时均方差无此倍数关系；深衰落点无法得到有效跟踪，峰值区域跟踪过度。

4.3 Δ的影响

4．3 ．1 仿真实验参数

Δk不同其他条件相同仿真实验参数见表10。

4．3 ．2 仿真实验分析

Δ不同得到的仿真实验结果如图8所示，选择与图8对应的连续300、750和1 500个采样点在平面图形中展开，m=100万，Δk=0．1 dB/cm，结果发现：相同物理条件下，均方差随着Δ的增大而增大，即整体的跟踪性能变差；某些深衰落点无法得到有效跟踪。

通过以上仿真实验发现，叙述中的方法并不能很好地跟踪深衰落区域和峰值区域，因此本文提出基于二次差分概率的无线信道估计方法。

5 改进方法提案

5.1 改进方法

由于方法叙述中的步骤4和步骤5只考虑了衰落曲线的整体跟踪性能，并未涉及深衰落区域和峰值区域的跟踪，导致曲线在深衰落点的跟踪性能下降，当衰落达到-10 dB以后基本无法跟踪，而某些峰值点则出现跟踪过度的现象。本研究提出的改进方法是在步骤5后，通过引入二次差分对深衰落区域和峰值区域估计差分值进行改善，具体方法如下。

（1）对深衰落区域的估计差分值进行改进

条件4 既是谷值点又满足二次差分值大于12 dB/cm条件的差分值ki1个数为s1，即ki1与其下一时刻ki1+1满足条件 ki1＜0，ki1+1＞0。

图7 Δk不同时真实值和估计值的采样对比

条件 5 ki1的上一时刻差分值 ki1-1属于不同的子区间，这些子区间的个数为tt2。

条件6 ki1落入某个子区间，并满足其对应的二次差分值大于12 dB/cm条件的下一时刻所有差分值ki1-1个数为nr1(r1=1,2,…,tt1)。

改进步骤1 对差分值进行二次差分，即：

图8 Δ不同时真实值和估计值的采样对比

通过实验数据发现当eki＞12 dB/cm时，基本能满足Ai＜-10 dB。eki为二次差分值，ki为当前时刻差分值，ki+1为下一时刻差分值，Ai为当前时刻增益值，i=1,2,…,m-2。

改进步骤2 找到衰落曲线的谷值，即ki＜0且ki+1＞0。找到既满足谷值点又满足eki＞12 dB/cm条件的差分值ki1。其中，ki为当前时刻差分值，ki+1为下一时刻差分值，eki为二次差分值，i=1,2,…,m-2，i1=1,2,…,s1。

改进步骤 3 判断 ki1上一时刻的差分值 ki1-1所属子区间 [mink+wΔk,mink+(w+1)Δk]，求出落入此子区间并满足eki＞12 dB/cm条件的差分值的下一时刻所有差分值kp1。对这些差分值求平均值，所得结果作为该子区间当前时刻估计差分值的修正值，即：

nr2为满足eki＞12 dB/cm条件下落入每个子区间的差分值个数，p1=1,2,…，nr1，w=0,1,…,tt1-1，r1=1,2,…,tt1。

（2）对峰值区域的估计差分值进行改进

条件 7 满足峰值条件的差分值为 ki2的个数为 s2，ki2为对应当前时刻的差分值，即 ki2与其下一时刻 ki2+1满足条件 ki2＜0，ki2+1＞0。

条件 8 二次差分值 ek的最大值和最小值分别为minek、maxek，区间范围是[minek,maxek]。

条件 9 ki2的上一时刻差分值 ki2-1属于不同的子区间，这些子区间的个数为tt2。

条件10 eki所属不同的子区间，这些子区间的个数为 tt3。

条件11 落入子区间[mink+lΔk,mink+(l+1)Δk]的差分值个数为nr2(r2=1,2,…,tt2)。

条件12 落入子区间[minek+lΔk,minek+(l+1)Δk]的二次差分值个数为nr3(r3=1,2,…,tt3)。

改进步骤4 找到衰落曲线的峰值，即ki＞0且ki+1＜0。找到满足峰值条件的差分值ki2。其中，ki为当前时刻差分值，ki+1为下一时刻差分值，i=1,2,…,m-2，i2=1,2,…,s2。

改进步骤 5 判断 ki2上一时刻的差分值 ki2-1所属子区间[mink+lΔk,mink+(l+1)Δk]，求出落入此子区间的所有差分值的位置qnr2。找到下一时刻对应的二次差分值eki（位置为qnr2+1）。其中，l为某一自然数，r2=1,2,…,tt2。

改进步骤6 以Δk对二次差分值ek进行区间划分，找到 eki属于的区间范围[minek+lk,minek+(l+1)Δk]，找到属于此区间的所有二次差分值eki1所在的位置qqnr3。其中，l为某一自然数，r3=1,2,…,tt3。

改进步骤7 找到位置qqnr3对应的差分值kp2，对这些差分值求平均值，所得结果作为当前估计差分值的修正值，即：

其中，p2=1,2,…,nr3，r3=1,2,…,tt3。

改进步骤 8 将深衰落区域和峰值区域修正过的估计差分值记为^kii。通过差分计算得到新的估计增益为：

其中，^Aii为改进后当前时刻估计增益，^Aii+1为改进后的下一时刻估计增益，^kii为改进后估计差分值，Δ为空间采样间隔，ii=1,2,…,m-1。

5.2 改进后的仿真实验分析

为了与图7和图8比较，新的仿真实验也主要讨论Δk和Δ的影响。

5．2．1 Δk的影响

Δk不同时改进方法的仿真实验参数与表9相同，仿真实验结果如图9所示，其中，m=100万，Δ=0．1 λc。选择与图7对应的连续150个采样点，在平面图形中展开，结果发现：相同物理条件下，随着Δk的增大，均方差变化非常小；改进曲线在峰值区域跟踪过度的现象减弱，且能够良好地跟踪深衰落区域；对比图7和图9，当Δk=0．05 dB/cm时，σ由3．171 5 dB减小到2．131 2 dB；当Δk=0．1 dB/cm时，σ由3．173 4 dB减小到2．132 8 dB；当Δk=0．2 dB/cm时，σ由3．177 1 dB减小到2．140 3 dB。即改进后真实增益和估计增益的误差均方差减小，整体跟踪性能也明显增强。

5．2．2 Δ的影响

不同时改进方法的仿真实验参数与表10相同，仿真实验结果如图10所示。选择与图8对应的连续300、750和1 500个采样点在平面图形中展开，结果发现：相同物理条件下，Δ越小，曲线跟踪性能越好；改进曲线在峰值区域跟踪过度的现象减弱，且能够良好的跟踪深衰落区域；当Δ= 0．1λc时，σ由3．173 4 dB减小到2．132 8 dB；当Δ=0．05λc时，σ由1．790 6 dB减小到1．312 2 dB；当Δ=0．02λc时，σ由 0．986 3 dB减小到 0．6181 dB；当 Δ=0．01λc时，σ由0．691 3 dB减小到0．516 7 dB。即改进后真实增益和估计增益的误差均方差减小，整体跟踪性能也明显增强。

6 结束语

本文对基于差分概率的信道衰落估计方法进行研究，分析了最佳集合长度，通过引入二次差分提出了基于二次差分概率的无线信道估计方法，该方法主要是对深衰落区域和峰值区域的估计差分值进行改善，仿真实验结果表明所提新方法能有效地跟踪深衰落和峰值区域，并降低曲线的跟踪误差。本文所提到的新方法依旧只是进行差分及差分概率的运算，方法简单、易于操作。

图9 Δk不同时真实值和估计值的采样对比

图10 Δ不同时真实值和估计值的采样对比

[1]陆琦.无线通信衰落信道的实现[D].大连:大连海事大学,2007. LUQ.Therealizationoffadingchannelsforwirelesscommunication[D]. Dalian:Dalian Maritime University,2007.

[2]SINGH Y.Comparison of Okumura,Hata and COST-231 models on the basis of path loss and signal strength[J].International Journal of Computer Applications,2012,59(11):37-41.

[3]张鑫,黄进文.移动通信中 Okumura和 Walfisch-Bertoni传播预测模型对比浅析 [J].科技信息:学术研究,2007(35): 86-90. ZHANG X,HUANG JW.ComparisonofOkumuraand Walfisch-Bertoni propagation prediction models in mobile nommunication[J].Scientific Information:Academic Research,2007(35):86-90.

[4]NADIR Z,AHMAD M I.Characterization of pathloss using Okumura-Hata model and missing data prediction for Oman[J]. 2010,1285(1):509-518.

[5]COTA N,SERRADOR A,VIEIRA P,et al.On the use of Okumura-Hata propagation model on railway communications[J]. Wireless Personal Communications,2013,6983(6):1-5.

[6]MARDENI R,PRIYA T S.Optimised COST-231 Hata models for WiMAX path loss prediction in suburban and open urban environments[J].Modern Applied Science,2010,4(9):75-89.

[7]SHABBIR N,SADIQ M T,KASHIF H,et al.Comparison of radio propagation models for long term evolution(LTE)network[J]. International Journal of Next-Generation Networks,2011,3(3): 27-41.

[8]JOSEPH I.CDMA2000 radio measurements at 1.9GHz and comparison of propagation models in three built-up cities of south-south,Nigeria [J].American JournalofEngineering Research,2000,2(5):96-106.

[9]DALKILIC T E,HANCI B Y,APAYDIN A.Fuzzy adaptive neural network approach to path loss prediction in urban areas at GSM-900 band[J].Turkish Journal of Electrical Engineering &Computer Sciences,2010,18(6):1077-1094.

[10]JAIN R,SHRIVASTAVA L.Performance evaluation of AODV,SR, DYMO & ZRP in Cost231 Walfisch-Ikegamipath loss propagation model[J].Oeconomics of Knowledge,2011,3(3):2-15. [11]JOSHI S,GUPTA V.A review on empirical data collection and analysis of Bertoni’s model at 1.8 GHz[J].International Journal of Computer Applications,2012,56(6):17-23.

[12]楚高峰.认知无线电中信道估计技术的研究 [D].重庆:重庆邮电大学,2011. CHU G F.Research on channel estimation technology in cognitive radio[D].Chongqing:Chongqing University of Posts and Telecommunications,2011.

[13]GE X,TU S,HAN T,ET al.Energy efficiency of small cell backhaul networks based on Gauss-Markov mobile models[J]. Networks IET,2014,4(2):158-167.

[14]王智森,王洪海,房媛,等.移动无线信道的数学仿真计算[J].大连工业大学学报,2009,28(5):370-374. WANG Z S,WANG H H,FANG Y,et al.Mathematical simulated calculation of mobile wireless channel[J].Journal of Dalian Polytechnic University,2009,28(5):370-374.

[15]王智森,浦良,潘登,等.一种窄带信道增益估计方法: 201010536771.4[P].2010-11-09. WANG Z S,PU L,PAN D,et al.A method of narrowband channel gain estimation:201010536771.1[P].2010-11-09.

[16]BOGDANOVIC M.Frequency domain based LS channel estimation in OFDM based power linecommunications[J]. Automatika,2014,55(4):487-494.

[17]JO J,SOHN I.On the optimality of training signals for MMSE channel estimation in MIMO-OFDM systems[J].EURASIP Journal on Wireless Communications and Networking,2015(1):1-9.

[18]张建康,穆晓敏,陈恩庆,等.OFDM系统基于导频的信道估计算法分析[J].通信技术,2009,42(8):91-94. ZHANG J K,MU X M,CHEN E Q,et al.Pilot-based channel estimation algorithms for OFDM system [J].Communications Technology,2009,42(8):91-94.

[19]AGYAPONG P K,IWAMURA M,STAEHLE D,et al.Design considerations fora 5G network architecture [J].IEEE Communications Magazine,2014,52(11):65-75.

[20]WUNDER G,JUNG P,KASPARICK M,et al.5GNOW:nonorthogonal,asynchronouswaveformsforfuturemobileapplications[J]. IEEE Communications Magazine,2014,52(2):97-105.

[21]GE X,ZI R,WANG H,et al.Multi-user massive MIMO communication systems based on irregular antenna arrays[J].IEEE Transactions on Wireless Communications,2016,15(8):1-15.

[22]CHEN S,ZHAO J.The requirements,challenges,and technologies for 5G of terrestrial mobile telecommunication[J]. IEEE Communications Magazine,2014,52(5):36-43.

[23]张建敏,谢伟良,杨峰义.5G超密集组网网络架构及实现[J].电信科学,2016,32(6):36-43. ZHANG J M,XIE W L,YANG F Y.Architecture and solutions of 5G ultra dense network [J].Telecommunications Science, 2016,32(6):36-43.

[24]陈山枝.发展5G的分析与建议 [J].电信科学,2016,32(7): 1-10. CHEN S Z.Analysis and suggestion of future 5G directions[J]. Telecommunications Science,2016,32(7):1-10.

[25]RAPPAPORTTS.Wirelesscommunicationprinciplesandpractice[M]. New York:Prentice Hall,1996:139-140.

Radio channel estimation method based on quadratic differentials probability

WANG Lijiao,DU Weiwei,LI Fan,WANG Zhisen
School of Information Science and Engineering,Dalian Polytechnic University,Dalian 116034,China

The fifth generation(5G)mobile communication technology has the characteristics of high speed and large bandwidth,which makes the fading of radio signal in time domain and frequency domain more obviously．With the increase of differential values statistical step and the spatial sampling interval,the channel estimation method based on the differential probability can’t track the deep fading area and the peak area was over-tacked．In view of the above problems,a channel estimation method based on quadratic differentials probability was proposed．Firstly,the valley point and peak point of the fading curve were found．Then,the estimated differential values of deep fading area and peak area were improved by quadratic differential probability．Finally,the estimated gains were obtained by the difference operation．Simulation results show that,this method can improve the whole tracking performance effectively and reduce the tracking error．

5G,mobile radio channel,channel estimation,differentials probability,quadratic differentials

TN929．5

A

10．11959/j．issn．1000-0801．2017015

王立姣（1990-），女，大连工业大学硕士生，主要研究方向为通信与物联网。

杜薇薇（1994-），女，大连工业大学硕士生，主要研究方向为通信与物联网。

李凡（1992-），女，大连工业大学硕士生，主要研究方向为通信与物联网。

王智森（1963-），男，博士，大连工业大学信息科学与工程学院院长、教授，集成测控技术研究所所长，主要研究方向为无线通信与网络、数字信号处理、物联理论与物联技术。

2016-12-04；

2017-01-05