基于最小二乘支持向量机的心音分类识别研究

许莉莉，师炜，郭学谦，曲典

首都医科大学 生物医学工程学院 临床生物力学应用基础研究北京市重点实验室，北京 100069

基于最小二乘支持向量机的心音分类识别研究

许莉莉，师炜，郭学谦，曲典

首都医科大学 生物医学工程学院 临床生物力学应用基础研究北京市重点实验室，北京 100069

目的将最小二乘支持向量机引入心音的分类识别，优化其参数设置，获得最优的分类结果。方法本文通过医院采集和网络下载获得99例心音信号，每个信号提取两个长度为5 s的样本，共198个样本，均分为3个集合。对每个样本采用sym6小波基进行小波包3层分解，根据Parseval定理计算每个样本的能量谱特征。以训练集数据送入支持向量机和最小二乘支持向量机进行机器学习，采用不同步长相结合的搜索法，根据测试集1的分类结果对向量机的参数进行优化。结果以高斯径向基函数为核的支持向量机，其惩罚因子C和核函数宽度σ均为20.086时，对测试集1的分类正确率最高，为79.7%；对测试集2的分类正确率为84.5%，分类计算使用的时间分别为0.108 s和0.117 s。对最小二乘支持向量机，高斯径向基函数宽度平方σ2取1，正则化参数γ取20.086时，对测试集1的分类正确率最高，为94.2%；对测试集2的分类正确率为89.6%，分类计算使用的时间分别为0.0638 s和0.0692 s。结论采用求解线性方程法寻找局部最优解的最小二乘支持向量机运算速度快，更适合心音样本的分类识别。

心音；小波包分解；支持向量机；最小二乘支持向量机；参数优化

引言

心音信号是人体最重要的生理信号之一，是心脏瓣膜的开关、肌腱和肌肉的舒张、血流的冲击及心血管壁的振动而产生的一种复合音[1]，包含丰富的关于人体心脏和血管的生理及病理信息，是了解心脏和心血管状态的有效手段[2]。通过心音信号检测和分析来提示心血管系统的某些病变，是心脏疾病辅助诊断的有效手段。有研究表明，某些心血管疾病，在导致心电信号出现异常之前，首先导致心脏杂音和心音变异，因此，心音是这些诊断这些疾病的最佳选择[3-4]。对心音信号的正确分类是实现监测心音、预警心血管疾病的关键技术。

目前，国内外对心音的研究集中在心音降噪、自动分段和分类识别上[5]。其中，心音降噪和自动分段是心音正常或异常识别的前期任务。近年来，文献报道多用haar，db，coif，sym等各种小波基对心音进行降噪处理[6]；采用小波、小波包分解，希尔伯特黄变换等方法对信号提取时频特征等[7]。在分类识别方面，支持向量机也成为主流分类方法[8-10]。但由于缺乏公认的心音数据库，各类文献报道的算法只针对各自的心音样本，互相之间也难以比较。随着心音样本的积累，善于处理小样本的支持向量机将会出现运算时间长，甚至无法给出最优解的问题。最小二乘支持向量机即保留了支持向量机原有的优势，又改变了求解最优解的方法，适用于样本数量增大时的分类识别，因此本文通过小波包分解提取心音样本的能量特征，结合最小二乘支持向量机对心音的正常和异常进行识别。

1 材料和方法

1.1 心音的采集和降噪

实验数据来源有两部分，一部分来自实测，录制异常心音的患者均由北京友谊医院确诊患有各类心脏病；录制正常心音的健康人群均经北京宣武医院体检无心脑血管疾病，且无心脏病史。实验中共采集异常心音19例，正常心音45例。录制心音使用的是合肥华科电子技术研究所研制的HKY-60C型心音传感器，在家用电脑上通过Cool Edit Pro2.0软件直接录制。录制过程中将心音传感器置于受检者的胸部来采集心音信号，采样频率为11025 Hz。另一部分心音信号来自互联网下载[11]，其中异常心音32例，正常心音3例，采样频率为22050 Hz。由于心脏是一个时变的复杂系统，受呼吸、心脏血流动力学状态以及人所处的环境等不确定因素的影响具有很强随机性[12]。尽管同一个人的心动周期大致平稳，但仍存在一些差异，因此实验对上述99例心音信号，每个信号提取2个长度为5 s的片段作为心音样本，共计198个心音样本。将心音样本按强度归一化处理后的结果，见图1（为了清晰显示，下采样至220 Hz）。实验所有数据处理在Matlab7.8.0上完成。

由于近年来，利用小波变换进行心音降噪的研究较为普遍，利用小波变换能在不需要任何先验知识的前提下，从含噪信号中估计出有用信号，我们选用了几种常见的小波进行对比后，采用db5小波对心音样本进行了降噪，并将降噪后的信号下采样为1102.5 Hz。

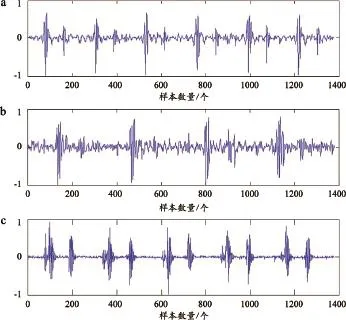
图1 心音样本按强度归一化处理后的结果

1.2 小波包分解

小波分解中，只对信号的低频部分作进一步的分解，因此小波变换的频率分辨率会随着信号频率的升高而降低。小波包分解能克服该缺陷对信号进行更精细的分析，通过对频带进行多层分解，以及对信号高频部分进行进一步的分解，从而更好地反映信号的本质特征。小波包3层分解树，见图2[9]。

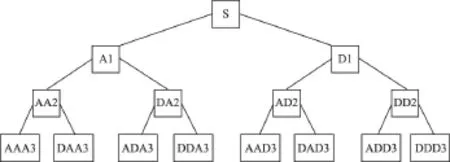
图2 小波包3层分解树

信号S(t)经过小波包分解，在第i层能得到2i个子带，即信号可表示为：

其中，Si,j(tj)为小波包分解在第i层节点(i,j)上的重构信号。

根据Parseval定理计算信号S(t)在小波包分解节点(i,j)上的能量为[13]：

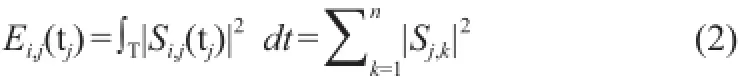
其中，n为子带采样点数，信号为离散数字信号时，按上式取求和方式计算子带能量。

本文对每个心音样本选用sym6小波基进行小波包3层分解，对每个小波包分解节点计算能量，构成一个8维的能量特征向量，用于心音样本的分类识别。

1.3 支持向量机和最小二乘支持向量机

支持向量机（Support Vector Machine，SVM）的理论最初来自于对两类数据分类问题的处理，其核心内容是Vapnik提出的结构风险最小化原则[14-15]，它能从有限的训练样本中得到较小误差，适用于不具备大量的病理样本而制约正确率提高的医学问题。对于给定的训练集，SVM考虑寻找一个最优分类面，不但要求要将两类训练样本无错误地分开，即保证经验风险最小；还要使两类的分类间隔最大，即使推广能力最强，从而保证真实风险最小。即对于给定样本集xi，i=1,2,…,n，构造一个目标函数，y = ω·x+b+ei，其中ω为n维权重向量，b为偏移量，ei为误差变量。寻找最优分类面既希望分类器错误分类的程度尽可能小，又希望两类间隔1/||ω||2尽可能大。故引入惩罚因子C控制训练错误率与分类器复杂程度间的折衷，则寻找最优分类面转化为最小化如下代价函数：

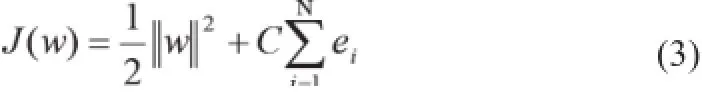
要在特征空间中找出这样的超平面，要求实现将非线性变换为线性分类，则要满足Mercer条件的核函数来构造输入空间。常见的SVM核函数包括线性核函数、多项式核函数、高斯径向基核函数以及sigmoid核函数等。其中高斯径向基核函数更加符合特征提取的要求，使用相对较多，它有两个控制参数，即核函数宽度σ(sig)和惩罚因子C。

最小二乘支持向量机（Least Squares Support Vector Machine，LS-SVM）是SVM的扩展[16]，它的代价函数变为：

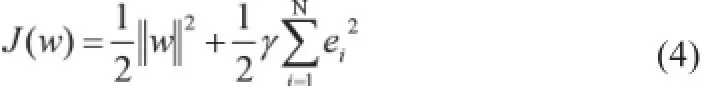
在实际的应用中，核函数通常也选择高斯径向基函数：K(x1, x2) = e-|x1-x2|2/2σ2。因此，核函数的宽度平方σ2(sig2)和正则化参数γ(gam)是LS-SVM必须调整的两个参数。SVM和LS-SVM的不同在于：① 两者的代价函数不一样，SVM选用的是误差（或称为松弛变量），LS-SVM选用的是误差的二次项；② 两者的优化方法不同[16-17]。

3 讨论

实验中将所有心音样本均分为3个样本集，各66例。一个作为训练集，用于SVM和LS-SVM的机器学习，测试集1用于优化分类器的参数，测试集2用于对优化后SVM和LS-SVM的测试。

本文采用正确率、灵敏度和特异性3个指标来考察SVM和LS-SVM的分类性能，其定义分别如下：

其中，真阳性为正确判断的异常心音样本数，假阳性为错误判断为异常心音的正常心音样本数，真阴性为正确判断的正常心音样本数，假阴性为错误判断为正常心音的异常心音样本数。

SVM和LS-SVM的分类性能均取决于参数的选择，其参数的选择并没有一定的规律，因此本文采用搜索法寻求最优参数组合[18]。每个参数的取值范围略有不同，作对数处理后将搜索步长设为1，在正确率高的区域再次对参数进行搜索，搜索步长设为0.2。

在SVM的实验中，以高斯径向基函数为核能使不同类别的样本在特征空间中距离尽可能大，而同类别样本间的距离又尽可能小。其核函数表达式为K(x1, x2) = e-|x1-x2|2/2σ2，σ为高斯函数的宽度，控制了函数的径向作用范围。惩罚因子C取值范围为e-1～e5，σ取值范围为1～e5，以训练集训练SVM，以测试集1优化参数C和σ。当惩罚因子C和核函数参数σ均取20.086时，SVM的分类正确率最高。取此参数组合对测试集2进行分类识别，结果见表1。

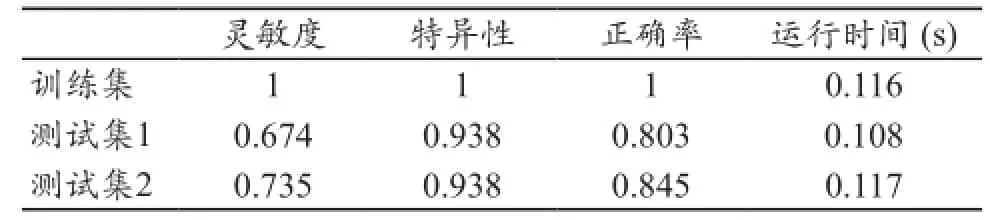
表1 SVM对测试集分类识别结果

采用相同的参数优化方法对LS-SVM的参数优化，结果表明σ2（sig2）取1，正则化参数γ(gam)为20.086时，LS-SVM的分类正确率最高。仍取该参数组合，对测试集2进行测试，结果如见表2。

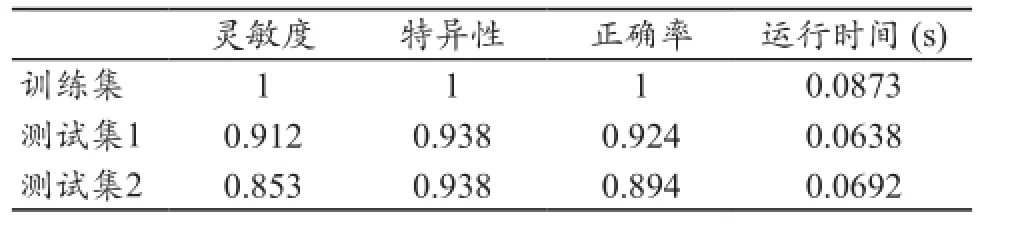
表2 LS-SVM对测试集分类识别结果

本文使用的心音样本中，正常和异常样本的数目大致相当，正常心音样本特征比较统一，因此不管是SVM还是LS-SVM的特异性都比较高。灵敏度主要是对异常心音识别的判别，其数值相对较低，这是由于在实验中使用的异常心音的种类繁多，引起心音异常的原因各不相同，使得异常心音样本在特征空间中分布松散不集中，不易被完全正确分类。而且SVM和LS-SVM表现出特异性数值相等，很可能是正常心音样本中，存在几个与一般正常心音差异较大的样本，总被误判为异常样本。

从表1～2的分类识别结果来看，LS-SVM的计算速度明显优于SVM且正确率更高，这是由于LS-SVM采用的损失函数是误差的二次项，它比SVM采用的误差项要更加敏感，并能将原来的SVM采用的求解一个凸二次规划问题转变为求解线性方程问题，降低了计算复杂度；SVM求解出来的是一个全局最优解，计算量大，耗时长，而LSSVM接受局部最优解，计算速度快[14]。

一般来说，SVM寻找到局部最优解，其分类识别的正确率应该比LS-SVM更高一些，在本文讨论的心音样本中，由于SVM和LS-SVM都对训练集做出了完全正确的分类，因此未体现出SVM全局最优解的优势。从测试集的结果来看，LS-SVM分类器更适应本文采集的心音样本的识别。但显然，即使是LS-SVM对心音样本分类的正确率还有很大的提升空间，今后我们考虑可以再增加样本其他方面的特征，即增加特征的维数以提高分类的正确率。

4 结论

本文讨论了SVM和LS-SVM在以小波包分解能量谱为特征的心音样本识别中的应用。从分类识别结果来看，LS-SVM具有计算速度快，分类识别正确率高的优势，更加实用于本文录制的心音的分类，也可用于临床上对心血管疾病的辅助诊断。若配合心音传感器，可在家庭电脑上录制心音信号，采用优化后的LS-SVM检测心音的正常与否，对心血管疾病能起到家庭预警的作用。

[1] 徐成斌.心音图学[M].北京:科技出版社,1982:6-7.

[2] 成谢峰,马勇,刘陈,等.心音身份识别技术的研究[J].中国科学:信息科学,2012,42(2):235-249.

[3] BENDER JR.Yale university school of medicine heart book[M]. New York:Willian Morrow and Company,1992.

[4] 李江,李晓玉.基于HHT的心音分段和医学指标提取[J].控制工程,2015,22(1):164-169.

[5] 成谢峰,张正.一种双正交心音小波的构造方法[J].物理学报,2013,62(16):168701.

[6] Liu F,Wang Y,Wang Y.Research and Implementation of Heart Sound Denoising[J].Phy Proc,2012,25:777-785.

[7] 王燕,王海滨,刘立汉.基于小波变换的心音信号降噪方法[J].太赫兹科学与电子信息学报,2010,8(3):303-307.

[8] Wang Y,Li W,Zhou J,et al.Identification of the normal and abnormal heart sounds using wavelet-time entropy features based on OMS-WPD[J].Fut Gener Com Sys,2014,37(7):488-495.

[9] 郭兴明,丁晓蓉,钟丽莎,等.小波包与混沌集成的心音特征提取及分类识别[J].仪器仪表学报,2012,33(9):1938-1944.

[10] 郭兴明,汤丽平.基于小波变换和样本熵的心音识别研究[J].计算机应用研究,2010,27(12):4555-4557.

[11] 最新心肺听诊音MP3全集(包含64个文件最全版)[DB/OL]. http://www.sobaidupan.com/f i le-15115158.html.

[12] 成谢峰,马勇,刘陈,等.心音身份识别技术的研究[J].中国科学:信息科学,2012,42(2):237-251.

[13] 肖玉飞,刘祖润,李目.基于小波包能量熵与SVM的模拟电路故障诊断[J].电子测量技术,2011,34(6):110-113.

[14] Vapnik V.The nature of statistical learning theory[M].New York:Springer Science & Business Media,2013.

[15] 姬水旺,姬旺田.支持向量机训练算法的实验比较[J].计算机应用研究,2004,(11):18-20.

[16] Suykens JAK,Gestel TV,Brabanter JD,et al.Least Square Support Vector Machine[J].Euphytica,2002,2(2):1599-1604.

[17] 阎威武,邵惠鹤.支持向量机和最小二乘支持向量机的比较及应用研究[J].控制与决策,2003,18(3):358-360.

[18] 朱向荣,单杨,李高阳,等.基于最小二乘支持向量机的国公酒中橙皮苷含量检测[J].光谱学与光谱分析,2009,29(9):2471-2474.

本文编辑 袁隽玲

Heart Sound Recognition Based on Least Squares Support Vector Machines

XU Li-li, SHI Wei, GUO Xue-qian, QU Dian
School of Biomedical Engineering, Capital Medical University, Beijing Key Laboratory of Fundamental Research on Biomechanics in Clinical Application, Capital Medical University, Beijing 100069, China

ObjectiveTo introduce the least square support vector machine (LS-SVM) into the recognition of heart sound, as well as optimizing its parameters setting to obtain the optimal classif i cation results.Methods99 heart sounds were obtained from our hospital and the internet. Two samples of 5 s were extracted from each heart sound to construct one training set and two test sets. 3-layer wavelet packets decomposition of sym6 was applied to each sample to extract feature. Then, the training set was used to machine learning of SVM and LS-SVM. One test set was used to parameters optimization, the other was for test of optimized SVM and LS-SVM.ResultsThe C and σ of the SVM that examined by Gaussian radial basis function were both 20.086. The accuracy for fi rst test set was the highest (79.7%). For second test set, the accuracy was 84.5%, and the running times were 0.108 s and 0.117 s, respectively. For the LS-SVM, the accuracy for fi rst test set was the highest (94.2%) while σ2=1 and γ=20.086. For second test set, the accuracy was 89.6%, and the running times were 0.0638 s and 0.0692 s, respectively.ConclusionThe LS-SVM that fi nd local optimal solution based on the linear equation method can operate faster, and it is more suitable for recognition of heart sound samples.

heart sound; wavelet packets decomposition; support vector machine; least squares support vector machine; parameter optimization

R318；TP181

A

10.3969/j.issn.1674-1633.2017.04.011

1674-1633(2017)04-0038-04

2016-10-17

2016-11-30

首都医科大学基础-临床一般课题（15JL17）。

郭学谦，副教授，主要研究方向为医学图像处理。

通讯作者邮箱：phyally@ccmu.edu.cn