后缘可变弯度翼型在跨声速中气动特性分析
林义彪, 马贵春, 符文科, 王 迎
(中北大学机电工程学院, 太原 030051)
0 引言
近年来,智能可变形飞机已成为国内外研究的热点,在飞机飞行的过程中,改变飞机的气动外形,使飞机在各种环境下飞行都能保持最佳的气动性能[1]。由于机翼前后缘的偏转对机翼飞行气动特性影响最大,因此,在机翼前后缘有目的做到无缝光滑连续改变机翼前后缘弯度,能够很好提高飞机的飞行性能[2-4]。
早在1994年,密歇根大学Kota[5]教授在实现机翼前后缘变形研究中首次运用了柔性机构的设计思想,通过柔性机构驱动器来实现机翼前后缘弯度的改变。后又提出“顺从机构”概念[6],即利用单点驱动各个金属组成单元弹性变形使前、后缘发生连续无缝偏转变形。东京大学Yokozeki和Sugiur[7-8]设计出瓦楞结构的后缘连续无缝变形机翼,并进行气动分析,得出连续无缝变弯度翼型有更好的气动性能。Nguyen等人设计一种高升力连续可变弯度后缘翼襟[9],并进行风洞试验,得出该后缘翼襟能够为运输机提供高升力性能。
在国内,西北工业大学的杨智春教授对柔性后缘自适应机翼进行了概念设计[10-11],提出了以曲线逼近原理为基础,对可变后缘弯度转轴点布局进行优化翼肋机构的设计方法,得出圆弧型柔性后缘是最佳的方案。中国航天空气动力技术研究院陈钱[12-13]等对可连续光滑偏转后缘的变弯度翼型进行气动特性分析及实验研究,得出可连续光滑偏转后缘的变弯度翼型的流场分离特性和气动性能优于传统主翼——简单襟翼翼型。
目前国内外对后缘可变弯度研究主要放在设计优化方面,或低速状态下气动特性研究。文中在跨声速状态下,对后缘可变弯度不同弯度翼型进行气动特性分析,对可变弯度机翼应用到实际飞行中具有一定的参考价值和实际应用价值。
1 跨声速翼型气动特性理论分析
当来流马赫数大于临界马赫数(Ma∞>Macr),翼型表面上将出现局部超音速区和激波,这就变为跨声速流动。由于在跨音速中包含局部激波,且其流动是混合型的,就使得跨音速流动较亚音速流和超音速流要复杂得多,给理论分析和实验研究带来较大的困难。
由等熵流压强公式可得翼型表面某点Ma、p与来流Ma∞、p∞之比[14],即:
(1)
当p=pcr时,有Ma=1,Ma∞=Macr,由此得到临界压强系Cpcr数[14]为:
(2)
此为等熵流动中临界压强系数Cpcr与临界马赫数Macr的关系式。实际计算时,是按翼型最低压力点的压强系数求得,可按卡门钱学森公式求出[14],即:
(3)
在跨音速中,超临界翼型能够很好的提高飞机飞行的临界马赫数和阻力发散马赫数,提高飞机的高亚声速巡航速度。文中以超临界翼型DFVLR R-4为基础,进行后缘弯度连续变化得到不同后缘弯度翼型,并通过对其进行跨声速下气动力数值研究,通过翼型数值计算及压力图,分析其在跨声速的升阻特性以及抖动特性分析。
2 基于超临界翼型后缘可变弯度模型和与数值计算方法
2.1 临界翼型后缘可变弯度模型
NASA对VCCTEF进行了初步优化设计,得出用后缘中弧线作为抛物线轨迹变弯度的布局在改善巡航升阻比和压力分布方面是最优的[15]。以基本超临界翼型DFVLR R-4翼型为基本翼型,在后缘为30%弦长,向下分别偏转1°、2°、3°,得到3种可偏转翼型。图1中BA为DFVLR R-4翼型,Va-1为后缘向下偏转1°,Va-2为后缘向下偏转2°,Va-3为后缘向下偏转3°。
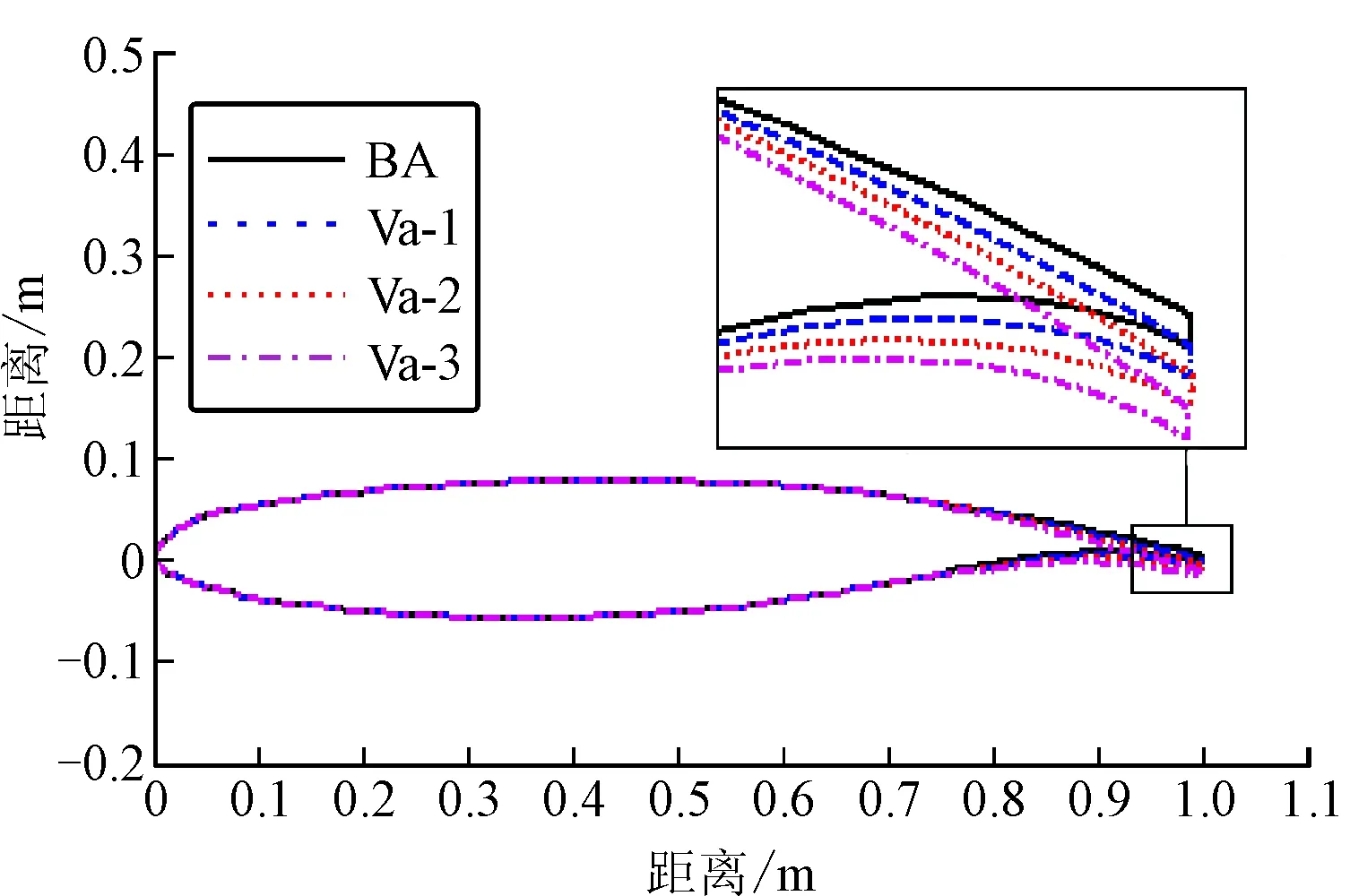
图1 超临界翼型后缘变弯度示意图
2.2 数值计算方法
对翼型后缘弯度变化结构进行分析,并依据求解雷诺平均Navier-Stokes(RANS)方程的CFD计算,本实验采用C-H结构网格,对面壁边界进行网格加密,网格如图2所示。通过有限体积法离散差分方程,湍流模型采用Spalart-Allmaras(S-A)模型,二阶迎风离散格式。

图2 翼型变弯度的CFD网格模型
3 数值分析
3.1 可变翼型变弯度升阻特性分析
对超临界翼型后缘可变弯度在跨声速中气动特性分析,首先要确定4种翼型的临界马赫数。图3是攻角为0°时基本翼型与3种变弯度翼型的临界马赫数变换趋势。从图3知基本翼型临界马赫数为0.686。Va-1翼型的临界马赫数为0.665,降低0.021个马赫数;Va-2翼型临界马赫数为0.642,降低了0.044个马赫数;Va-3临界马赫数为0.625,降低了0.061个马赫数。由此可知超临界翼型后缘弯度少量舵偏,就会降低翼型的临界马赫数,这对提高飞行器在跨声速中的巡航马赫数是不利的。
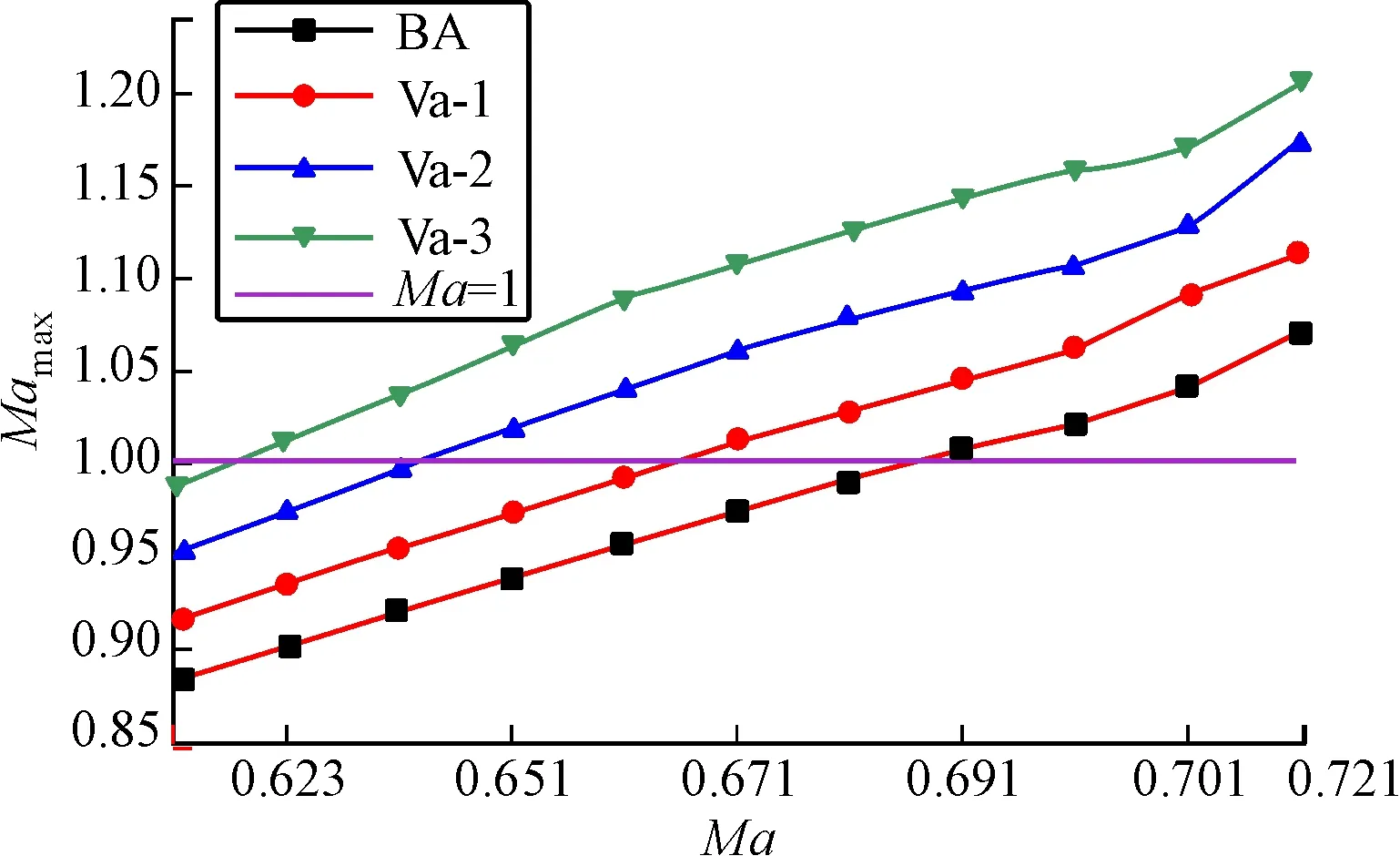
图3 翼型变弯度的临界马赫数
图4为4种翼型的升力系数随着来流马赫数增加的分布趋势。由图可知升力系数随着来流马赫数的增加呈现上升趋势,当来流马赫数继续增大时升力系数急剧下降,这是由于激波失速引起的。随着后缘弯度变化的增加,引起激波失速的来流马赫数提前;在来流马赫数相同情况下,随着后缘弯度系数的增加,升力系数提高。该翼型与某远程宽体客机机翼翼型相似,根据三维机翼巡航马赫数,按照后掠翼理论三维转换为二维后,得到该超临界翼型的设计马赫数为0.721。在来流马赫数为0.721Ma,Va-1翼型升力系数提高了21.12%,Va-2翼型升力系数提高了39.43%,Va-3翼型升力系数提高了47.74%,但Va-3翼型在0.711Ma已达到激波失速,在0.721Ma虽然升力系数大大提高,但翼型抖动性增加,不利于机翼在跨声速中的飞行。
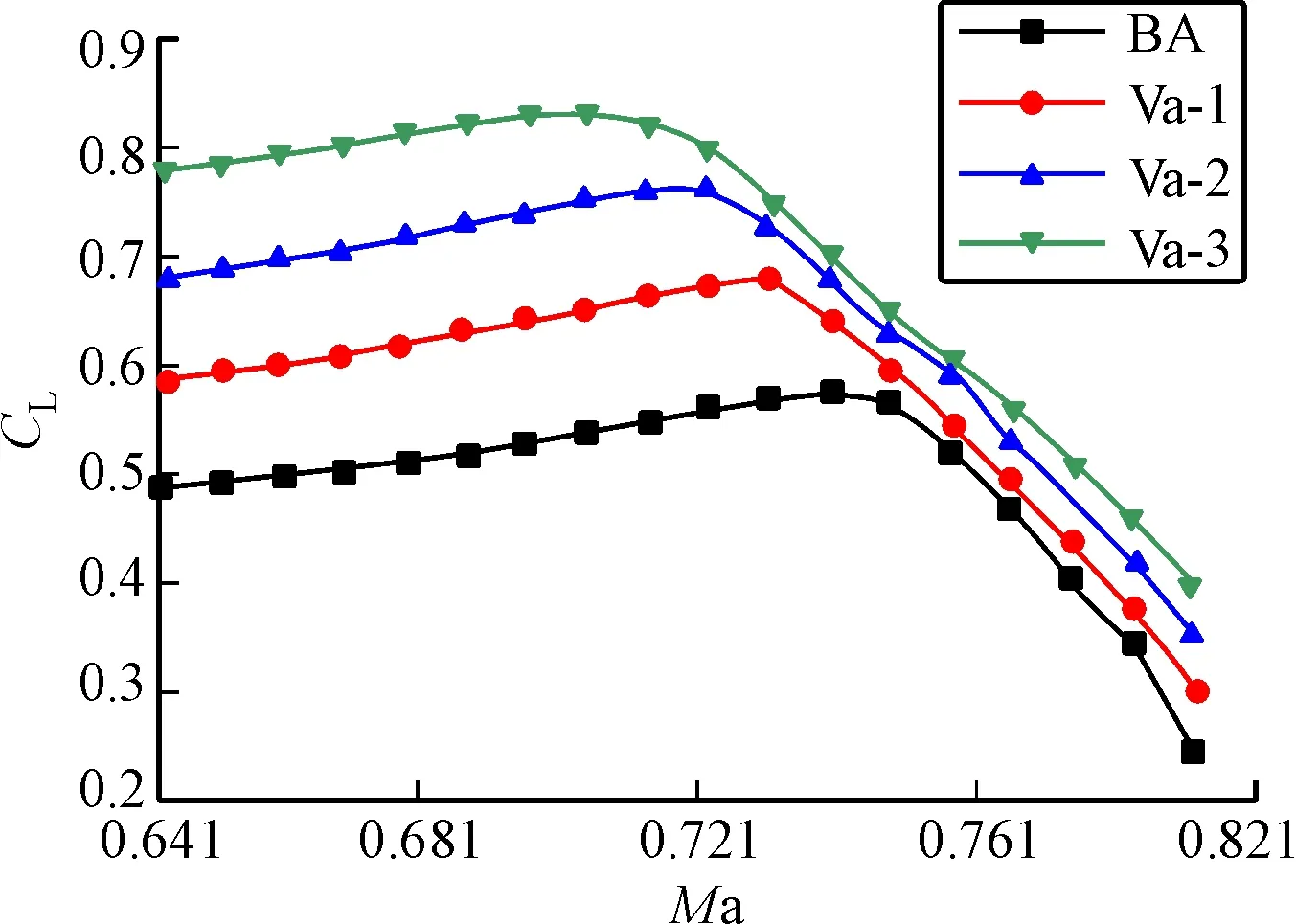
图4 不同后缘弯度翼型的升力系数分布
结合4种翼型的压力分布图来分析后缘可变弯度的升阻特性,如图5为4种翼型的压力系数分布,可以看出,当来流马赫数Ma∞>Macr,随着后缘弯度增加,翼型压力系数增大,其相应阻力系数增加;下表面压力系数围成的面积增加,此时表现为可变形机翼后缘弯度增加其升力系数增加。
当来流马赫数Ma∞=0.681,Va-3翼型较Va-2翼型激波前移,Va-2较Va-1翼型激波前移(Ma∞=0.681未达到BA翼型的临界马赫数)。来流马赫数Ma∞=0.701,Va-3翼型较Va-2翼型激波后移,且强度增大,翼型上表面压力系数出现抖动,其表现为阻力系数开始增大,升阻比开始下降;而Va-2翼型较Va-1翼型激波前移,Va-2较BA翼型激波前移。来流马赫数Ma∞=0.721,Va-3翼型较Va-2翼型激波后移,Va-2翼型较Va-1翼型激波后移且强度增加,Va-2较BA翼型激波前移,升阻特性变化趋势与上相同。来流马赫数Ma∞=0.741,随着后缘弯度的增加,其激波后移,激波强度增加,升阻比已开始下降。

图5 不同后缘弯度翼型的压力系数分布
由此得出,在一定的来流马赫数范围内(Macr 如图6为阻力系数随着来流马赫数的变化情况,由图可知在临界马赫数之前(Ma∞ 图6 不同翼型后缘弯度下的阻力系数分布 如图7为4种翼型的升阻比随来流马赫数增加变化情况,其影响趋势与可以由图5所示4种翼型相应的压力系数分布图来解释。来流马赫数M∞达到二维翼型的设计马赫数0.721时,Va-1翼型升阻比提高9.2%,Va-2翼型升阻比提高5.4%,Va-3翼型升阻比减少5.3%。根据图6所示4种翼型的压力系数分布在Ma∞=0.721,Va-2翼型与Va-3翼型其激波强度大大提高,且后移,翼型抖动性提高,不利于在Ma∞=0.721时巡航;Va-1激波增强不大,且前移,对机翼抖动性影响不大。由此可知,二维翼形的设计马赫数为0.721Ma,后缘可变弯度在1°之内,对机翼的跨声速飞行是有利的。 图7 不同后缘弯度翼型的升阻比分布 在二维翼型设计马赫数为0.721Ma,即来流马赫数Ma∞=0.721,4种翼型的其他条件相同。图8为4种翼型的升力系数随攻角的变化分布情况,由图可知随着翼型后缘弯度的增加,在相同攻角下其升力系数增加,随着攻角增加最大升力系数增加,随着升力系数增加引起的高速抖振特性得到改善。升力系数分布与图9在来流马赫数Ma∞=0.721,攻角α=3.7°,4种翼型的压力系数分布图知,4种翼型达到失速迎角后,随着翼型后缘弯度的增加,翼型上表面激波前移,使超临界翼型表面抖动性能得到改善。 图8 Ma=0.721可变后缘弯度翼型在不同攻角下的升力系数分布 图9 Ma=0.721,α=3.7°不同后缘弯度翼型的压力系数分布 通过对超临界翼型后缘可变弯度在跨声速中气动特性进行数值分析,得出以下结论: 1)随着超临界翼型后缘弯度增加,其临界马赫数增加,引起激波失速的来流马赫数提前,且阻力发散特性变差,不利于飞机在跨声速中飞行。 2)在相同来流马赫数情况下,随着后缘弯度的增加,其升力系数得到大大提升;翼型变化量在1°时,在跨声速中的气动特性较好,翼型升力系数提高了21.12%,并阻比提高9.2%。 3)在来流马赫数数Ma∞=0.721, 随着翼型后缘 弯度的增加,在相同攻角下其升力系数提高,最大升力系数提高,具有较好的失速迎角特性,抖动性能得到改善。 参考文献: [1] RODRIGUEZ A R. Morphing aircraft technology survey:AIAA 2007-1258 [R]. Reston: AIAA, 2007: 1-15. [2] STANEWSKY E. Aerodynamic benefits of adaptive wing technology [J]. Aerospace Science Technology, 2000, 4(7): 439-452. [3] STANEWSKY E. Adaptive wing and flow control technology [J]. Progress in Aerospace Sciences, 2001, 37(7): 583-667. [4] SPILLMAN J J. The use of variable camber to reduce drag, weight and costs of transport aircraft [J]. Aeronautical Journal, 1982,96(95): 1-9. [5] KOTA S. Shape control of adaptive structures using compliant mechanism: ADA 376 131[R]. Ann Arbor: Department of Mechanical Engineering and Applied Mechanicas, 2000:1-25. [6] LU Kerr-Jia, KOTA S. Design of compliant mechanisms for morphing structural shapes [J]. Journal of Intelligent Material Systems and Structures, 2003, 14(6): 379-391. [7] YOKOZEKI T, SUGIUR A,HIRANO Y. Development of variable camber morphing airfoil using corrugated structure [J]. Journal of Aircraft, 2014, 51(3): 1023-1029. [8] YOKOZEKI T, SUGIUR A,HIRANO Y. Development and wing tunnel test of variable camber morphing wing [C]∥AIAA SciTech. 22nd AIAA/ASME/AHS Adaptive Structures Conference. Reston: AIAA, 2014: 1-13. [9] NGUYEN Nhan T, PRECUP Nathan, LIVNE Eli, et al. Wind tunnel investigation of a flexible wing high-lift configuration with a variable camber continuous trailing edge flap design[C]// AIAA AVIATION. 33rd AIAA Applied Aerodnanics Conference. Reston: AIAA 2015:1-30. [10] 杨智春, 解江. 柔性后缘自适应机翼的概念设计 [J]. 航空学报, 2009, 30(6): 1028-1034. [11] 杨智春, 党会学, 解江. 基于动网格技术的柔性后缘自适应机翼气动特性分析 [J]. 应用力学学报, 2009, 27(3): 548-553. [12] 陈钱, 白鹏, 尹维龙, 等. 可连续光滑偏转后缘的变弯度翼型气动特性分析 [J]. 空气动力学学报, 2010, 28(1): 46-53. [13] 陈钱, 白鹏, 尹维龙, 等. 变弯度翼型特性数值与实验研究 [C]∥第二届近代实验空气动力学会议论文集北京: 原子能出版社, 2009: 64-70. [15] KAUL U K, NGUYEN N T. Drag optimization study of variable camber continuous trailing edge flap using overflow [C]∥AIAA AVIATION. 32nd AIAA Applied Aerodynamics Conference. Reston: AIAA, 2014:1-15.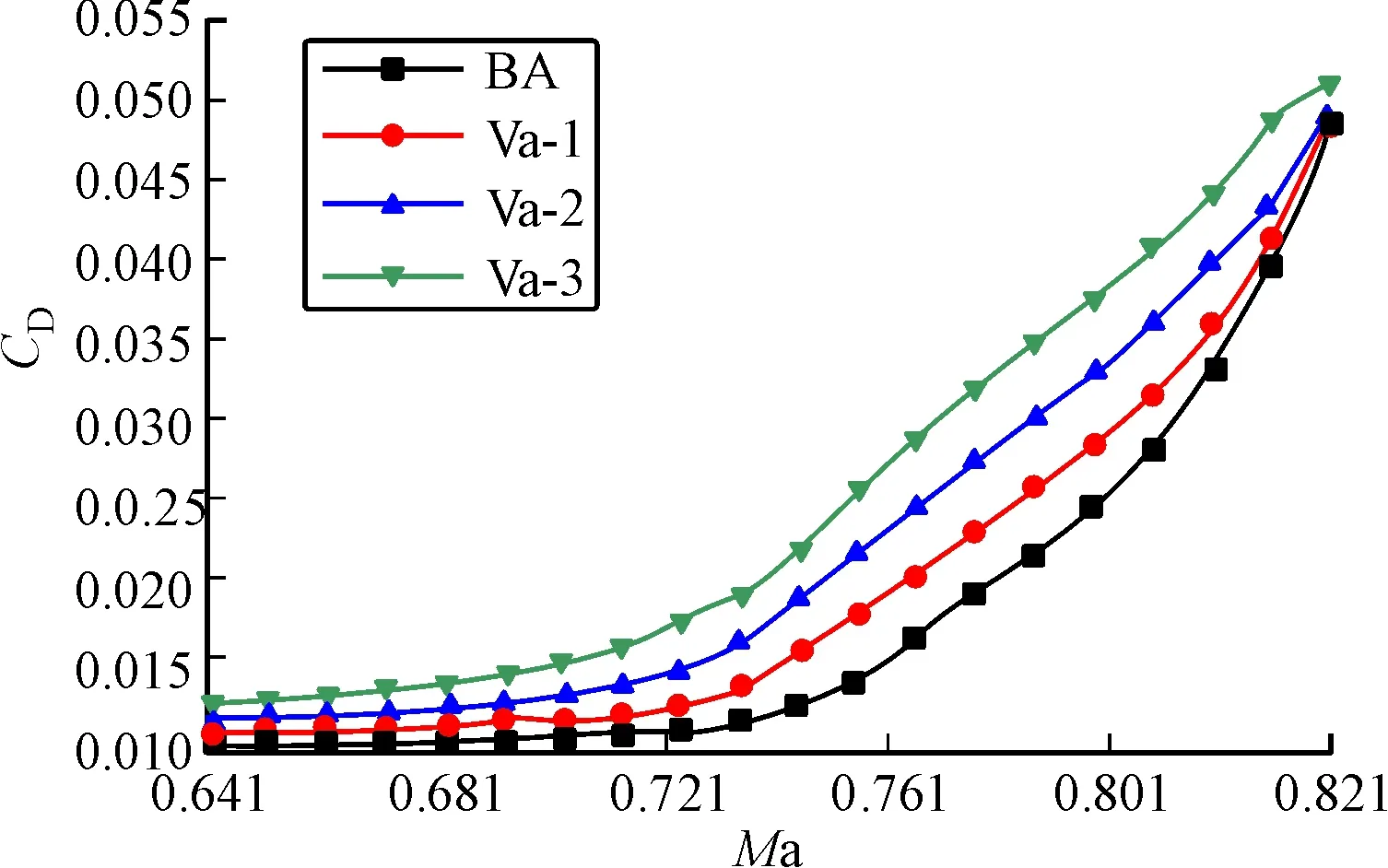

3.2 可变后缘弯度的失速迎角特性分析

4 结论

