从加减法的估算策略谈起
文︳胡文双
从加减法的估算策略谈起
文︳胡文双
一、加减法的估算策略
加减法估算的基本策略是取整:把一个一般的数看成整十数、整百数、整千数等进行估算。以下是人教版数学教材三年级上册的两个例题。
例1如图1所示,为了估算700-218,我们将218估成200,容易知道坐动车比坐飞机大约便宜500元。
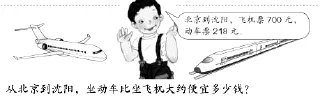
图1
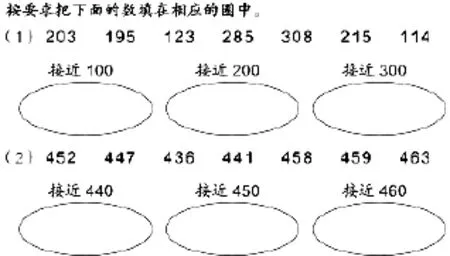
图3
例2如图2所示,为了估计245+187的和是否超过400,我们将245估成240,187估成180,240+ 180已经超过400了,于是245+187必然超过400。

图2
作为加减法的估算,以上两个例题中使用的策略便是取整。为了强化这一策略,教材中还编入了这样的练习题(如图3所示)。
二、加减法估算策略对除法估算的影响
因为在加减法的估算中强化了取整的策略,在除法估算时,学生面临一定的困难。比如,做如图4所示的练习时,学生估算78÷4和178÷6均很顺利,但在估算其他几题时均出现了困难。原因在于:估算78÷4和178÷6时,以前的取整经验依然管用——将78和178分别估成80和180,能顺利得到答案。但在对其他几题的估算中,原有的取整经验不能使用了——将361估成360,360÷ 5不易估算;将98估成100,100÷9不易估算;将470估成500,500÷8不易估算;而对于500,我们以前的经验是估算时不用额外处理,但现在500÷7学生不知如何估算。
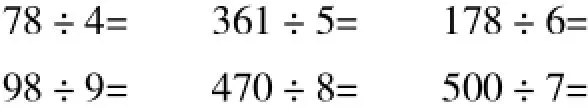
图4
三、教学处理
很多学生认为估算和精算一样,有一个固定的程序和一个唯一的结论。如果不知道这个固定的程序,就是不会估算;如果得出的估算结论与心中认为一定存在的某一个唯一答案不同,就一定是估算错了。
事实并非如此,估算问题是非常开放的。以估算361÷5为例,将361看成500,并由此估计361÷5大约为100;或者将361看成400,并由此估计361÷5大约为80;或者将361看成300,并由此估计361÷5大约为60,都不能算错。
因此,我们关于除法估算的第一个处理手段就是鼓励学生大胆地估,估算一般没有对不对的问题,只要言之成理就是对的,从而破除除法估算的神秘感,解决不会估的问题。教师可以通过类似上述估算361÷5的例子告诉学生:你不可能不会估。
其次,不能满足于能给出一个估计值,还要学会评价估算的策略。尽管估算通常没有对不对的问题,但还是有好不好的问题。怎样的估算是好的,怎样的估算是不太好的,评价的指标有两个,一个是计算量,另一个是精确程度。我们来看对361÷5的两种估算:
1.将361估成400,400÷5=80,于是361÷ 5≈80。
2.将361估成350,350÷5=70,于是361÷ 5≈70。
以上两种估算方法,计算量相差不大,但方法2得到的结果更精确,于是我们认为方法2比较好。
第三,如何找到好的估算策略。在上述除法的估算中,要找到好的估算策略,关键是确定把被除数估成哪一个数,能使计算量比较小,同时准确程度比较高。具体地说,在361÷5中,我们是如何知道要将361估成350的?其实基本思路就是乘法口诀。5的乘法口诀中,五七三十五,350比较接近361。同样地,对于500÷7,考虑7的乘法口诀,七七四十九,490接近500,于是可以将500看成490。
(作者单位:长沙市开福区育德小学)

