基于数学形态滤波和Hilbert－Huang变换的风电场闪变检测

李 骥 ，张 静，许童羽

（1．国网辽宁省电力有限公司 辽阳供电公司，辽宁 辽阳 111000；2．辽宁建筑职业学院，辽阳 111000；3．沈阳农业大学 信息与电气工程学院，沈阳 110866）

随着可再生能源和清洁能源的大力发展，越来越多的风电机组并网运行。风资源的不确定性和风电机组本身的运行特性，使风电机组的输出功率发生波动，电压波动和闪变成为风力发电对电能质量造成的主要负面影响之一，也成为限制风电场装机容量的重要因素之一。鉴于风电场引起闪变的随机性和波动性及其多种成因，采用一种适于分析非平稳、非线性信号的分析方法来分析风电场引起的闪变，准确地将闪变的参数信息量化，进一步将多种成因的影响量化，是有效抑制及治理风电场引起闪变的重要前提。

常见的闪变调制波检波方法有3种：平方解调法、全波整流法和半波有效值法。然而，电压波动与闪变根据不同扰动原因，有周期平稳性和时变非平稳性之分。这些方法均不适用于突变和时变的非平稳闪变信号的检测与分析。有研究采用快速傅里叶变换对闪变进行检测，这种方法认为信号是平稳的，因此分析非平稳信号时所得结果的精度会大大降低。也有研究提出了最小绝对值线性优化状态估计算法，但该方法推导复杂，缺乏快速算法。还有研究提出了基于小波变换的闪变信号检测方法，但是这种检测方法计算量大，小波基选择困难。

希尔伯特—黄变换 （Hilbert—Huang Transform，HHT）对于处理非线性、非平稳信号有清晰的物理意义，能够得到信号的时间—频率—能量分部特征。针对风电场引起闪变的特性，首先采用数学形态学滤波器滤除闪变信号中的多种噪声，然后采用Hilbert变换准确提取闪变包络信号，最后用HHT方法分析闪变的时频特性。该方法能够准确快速地提取闪变包络，进而有效检测出非平稳电压闪变的频率、幅值和时刻信息。

1 闪变检测原理

1.1 闪变数学模型

闪变信号可以看成是以工频电压为载波，电压均方根值受到电压波动分量调制的调制波。任何波形的调制波均可看作是各种频率分量的合成，如式（1）所示：

式中：A为供电电压的标称幅值；f，φ分别为基波频率和相角；Ak，fk，φk分别为调幅波分量的幅值（不超过基波幅值的10%）、频率 （一般觉察范围为1～25 Hz）和相角；A（t）为闪变包络信号，携带着闪变的幅值和频率信息。

分离出闪变包络是分析闪变的重要前提。通过Hilbert变换方法能够获得闪变包络信号，有研究验证了这种方法提取闪变包络的准确性，且通过比较得出，当含有单一和多个闪变频率的情况下，Hilbert变换较Teager能量算子法和IEC推荐的平方检测法在整个闪变频带范围内对包络的检测误差小且稳定性高。本研究选择Hilbert变换提取闪变包络。

1.2 Hilbert变换

给定一连续的时间信号x（t），其Hilbert变换定义为：

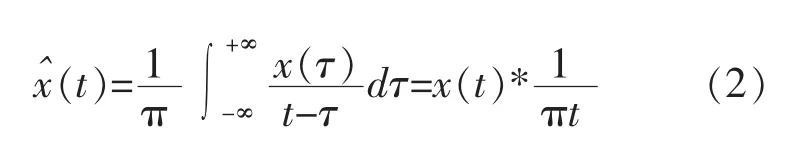
式中：*为卷积。

定义 x（t）的解析信号为：

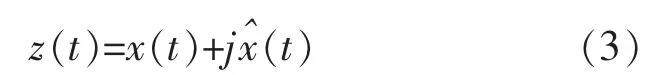
信号的瞬时幅值、瞬时相位和瞬时频率分别由以下各式求出：

对于含有高次谐波的调幅波信号，

其Hilbert变换为：

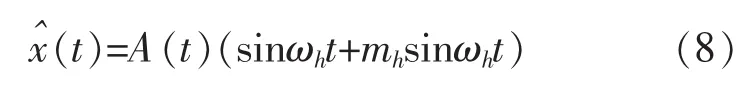
则

由式（9）可知，在含有高次谐波的情况下，直接使用Hilbert变换提取的闪变包络含有相同的谐波成分。同理，当闪变信号中含有白噪声、脉冲噪声时，Hilbert变换提取的闪变包络也含有噪声成分。因此，用Hilbert变换检测到准确闪变包络的前提是，首先滤除闪变信号中包含的多种噪声。

1.3 数学形态学滤波器的原理与设计

数学形态学（mathematical morphology，MM）在电力系统中的应用主要集中在信号消噪、电能质量扰动检测及定位等。基于数学形态学的腐蚀、膨胀、开运算和闭运算可以构建3种滤波算法：交替滤波器、混合滤波器、交替混合滤波器。

开—闭滤波器的输出幅度偏小，而闭—开滤波器的输出幅度偏大，所以单独使用交替滤波器不能取得较好的滤波效果；数学形态学滤波器的滤波效果与结构元素的形状及大小密切相关，经验表明，滤除白噪声使用半圆结构元素效果较好，对脉冲噪声采用三角形结构元素效果较好。本研究采用一种基于不同结构元素的级联复合数学形态学滤波器，每一级针对不同的噪声分别采用三角形、半圆形和直线形结构元素。三角形结构元素取值为［0，0.016 7，0.033 3，0.050 0，0.066 7，0.083 3，0.100 0，0.083 3，0.066 7，0.050 0，0.033 3，0.016 7，0］，半圆形结构元素半径为 0.05，长度为15，直线形结构元素长度为2，取值为0.01。滤波器结构如图1所示。

图1 复合数学形态学滤波器结构Figure 1 Framework of multiple MM filter

1.4 HHT方法

HHT方法包括经验模态分解 （empirical mode decomposition，EMD） 和 Hilbert变换两部分，Hilbert变换已在1.2节中解释，本节重点介绍EMD分解。

1.4.1 固有模态函数

使Hilbert变换得到的瞬时频率有意义的必要条件是：函数对称于局部零均值，具有相同的极值和过零点。据此，Huang提出了固有模态函数（Intrinsic Mode Function，IMF）的定义。一个IMF需是满足如下两个条件的函数：极值点和过零点的数量必须相等，或最多相差不多于一个；在任一时间点上，信号的局部极大值和局部极小值定义的包络平均值为零。

1.4.2 EMD算法

一般信号经常是复杂的信号，并不是IMF信号，用经验模态分解法可以将信号的IMF分量筛选出来。对于一个时间序列x（t），经验模态分解过程如下：1）确定原始信号x（t）的所有极大值点和极小值点；2）采用样条函数求出x（t）的上、下包络线，并计算均值m（t）；3） 作差 h（t）＝x（t）－m（t）；4） h（t）是否满足终止条件，若不满足将h（t）作为新的输入转至1），否则转至 5）；5） 令 c＝h（t），c 即为一个 IMF 分量，作差 r＝x（t）－c；6） 是否满足终止条件，若不满足则将 r作为新的输入转至1），若满足则EMD分解结束，不能提取的为残余量，为单调函数，表示信号的趋势。

对每个IMF分量作Hilbert变换可得Hilbert谱，进一步得到Hilbert边际谱，Hilbert边际谱提供了每一个频率值上分布的总的振幅或能量。

2 确定闪变的产生和终止时刻

设采样频率为3.2 kHz。原始闪变信号中含有的噪声包括白噪声（方差为0.01）、尖峰脉冲（幅值为0.30 pu）和高次谐波 （幅值为0.03 pu的3次和5次谐波）。

在0～4.5 s内除噪声分量外的闪变信号表达式为

0.83 ≤t≤3.66 时，p（t）＝1，其余时刻 p（t）＝0；ω＝6π r／s；i＝1，3，5。

采用1.3节设计的复合数学形态学滤波器对含噪闪变原始信号进行滤波，然后对去噪闪变信号进行EMD分解得到最高频的固有模态函数c1，根据式（6）求取c1的瞬时频率，从而可以确定闪变的产生和终止时刻。这一过程如图2所示。

图2 闪变产生和终止时刻的检测Figure 2 Detection of beginning and ending times of flicker

图2 （a）为含噪闪变原始信号，对去噪后的闪变信号进行EMD分解得到各IMF，再采用Hilbert变换求得最高频的固有模态函数c1的瞬时频率，即图2（c）。检测出c1的瞬时频率在0.827 s和3.664 s时各发生一次高频突变，表明信号在这两个时刻发生了变化，从而确定电压闪变的时间范围。与设定时刻相比，可见HHT方法可以精确地检测出电压闪变的产生和终止时刻，同时也验证了复合数学形态学滤波器的有效性。

3 闪变瞬时频率和幅值

设采样频率为3.2 kHz，噪声成分与上节相同。除噪声分量外的闪变信号表达式为：

u（t）＝［1＋0.05sin（24πt）＋0.1sin（4πt）］·cos（100πt）

首先采用1.3节设计的复合形态滤波器滤除含噪闪变原始信号中的各种噪声，然后对去噪后的闪变信号Hilbert变换求取闪变包络，最后对包络信号进行HHT时频分析，可以得到闪变信号的瞬时频率和瞬时幅值信息。此过程如图3所示。

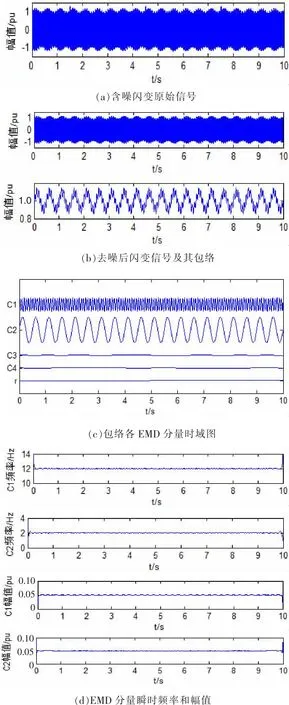
图3 闪变瞬时频率和幅值的检测Figure 3 Detection of instantaneous frequency and amplitude of flicker

EMD分解将包含闪变频率和幅值信息的闪变包络信号分解为由高频到低频的各IMF分量，如图3（c）所示。对图3（d）取均值得到的频率和幅值分别为12.082 Hz和 0.049 3 pu，误差分别为0.68%和1.40%，得到的频率和幅值分别为1.975 Hz和0.101 6 pu，误差分别为1.25%和1.60%。同时从闪变包络的边际谱可清晰看出不同频率分量对闪变的能量贡献。仿真数据表明，在含有多种噪声的情况下，该方法能准确地检测出多频率闪变的频率和幅值信息，从而对电压闪变参数进行准确量化。从分析的过程也可以看出HHT具有自适应性，不存在基函数选择的问题。

4 结语

本研究提出一种系统的、准确快速的闪变检测方法。仿真表明，复合数学形态学滤波器在保留闪变特征的前提下能有效滤除原始闪变信号中包含的多种噪声，在此基础上Hilbert变换能够准确提取闪变信号的包络，适于分析非平稳信号的HHT方法，从时频两方面对闪变包络信号进行频率和幅值的量化，最终准确检测出闪变的频率、幅值和时刻信息。面对风电场接入带来的严重闪变问题，本研究所提方法结合合理的风电场并网模型，能够对影响风电场引起闪变的多种因素进行有效分析和量化，从而指导风电场引起闪变的治理和辅助设备的研发。

［1］朱涛.风电场接入系统的相关问题研究综述［J］.南方电网术，2009，3（5）：58－69.

［2］齐勇，江亚群，黄纯.基于虚拟仪器的风电场电压闪变测量研究［J］.电测与仪表，2010（9）：1－4.

［3］朱雪凌，张洋，高昆.风电场无功补偿问题的研究［J］.电力系统保护与控制，2009，37（16）：68－76.

［4］SRINIVASAN K.Digital measurement of the voltage flicker［J］.IEEE Transactions on Power Delivery，1991，6（4）：1 593－1 998.

［5］SOLIMAN S A，EL－HAWARY M E.Measurement of power systems voltage and flicker levels for power quality analysis：a static lav state estimation based algorithm［J］.International of Journal of Electrical Power and Energy Systems，2000，22（6）：447－450.

［6］魏晓璞，徐永海，肖湘宁.电压波动与闪变检测方法综述［J］.电测与仪表，2009（4）：1－5.

［7］王秉均.通信原理及其应用［M］.天津：天津大学出版社，2000.

［8］贾秀芳，陈清，赵成勇，等.电压闪变检测算法的比较［J］.高电压技术，2009，35（9）：2 126－2 132.