品字形拼接探测器偏流角补偿研究

温 渊,张大伟

(上海卫星工程研究所,上海 201109)



品字形拼接探测器偏流角补偿研究

温 渊,张大伟

(上海卫星工程研究所,上海 201109)

对遥感卫星TDI-CCD推扫品字形探测器偏流角的补偿进行了研究。根据偏流角产生机理，用轨道要素法推导出一种简单可靠的偏流角计算和补偿方法，将偏流角补偿后重新计算的欧拉角作为控制目标输入闭环进行控制，规避了三轴欧拉角转序的影响。分析了偏流角控制对品字形拼接探测器成像产生的像元错位、调制传递函数(MTF)、通道间配准和幅宽等的影响。结果发现：对偏流角进行控制后穿轨向像元错位可消除，沿轨纵向像元错位不能消除，穿轨和沿轨向MTF均可消除，偏流角可对幅宽无影响；不对偏流角进行控制会严重影响通道间的配准精度。所提方法计算简单，流程清晰，在工程中有一定的应用价值。

遥感卫星； TDI-CCD推扫； 偏流角； 交错拼接； 补偿； 像元错位； 调制传递函数； 通道间配准； 幅宽

0 引言

美国的快鸟-2、Ikonos-2、GeoEye-1等商业遥感卫星的空间分辨率已突破了亚米级，最高达到了0.41 m[1]。我国在宽幅高分辨率对地遥感卫星领域与国际先进水平相比仍有较大差距[2]。大规模长线阵焦平面组件拼接和高精度偏流角补偿是高分辨率宽幅对地遥感首先要解决的两项关键技术。受制造工艺水平的限制，单片探测器的像元数及尺寸一般情况下不能满足宽覆盖成像需求，为获得大尺寸焦平面，常采用多片探测器进行品字形拼接成一个宽视场探测器阵列。探测器四周均存在抽头引线，无法排成一列直接拼接，目前主要有光学拼接和交错拼接两种方法，由于光学拼接会损失能量，目前更多选用交错拼接方式[3]。交错拼接将探测器分为两排，在沿推扫方向上交错排列。为防止漏扫，相邻探测器间存在一定的像元重叠数，对面阵探测器，则形成类似“品”字形的结构，又称“品字形拼接”[4]。品字形拼接探测器相同通道间在沿轨方向的距离较大，进行图像拼接及配准时需解决一系列问题。偏流角对单元探测器扫描成像并无影响，但对TDI-CCD推扫及品字形拼接推扫均存在影响，品字形拼接方式的两排探测器间有间隙，偏流角的存在影响此类探测器的成像效果。偏流角一方面会引起TDI-CCD的成像模糊，另一方面对品字形拼接探测器，由于存在较大的沿飞行方向的间隙，可导致相邻探测器间重叠像元数随卫星的星下点纬度发生剧烈变化，地面拼接图像时难以实现自动处理，需采用特殊处理办法，若重叠像元数不足，则有漏扫的风险[5]。严格计算偏流角的计算量较大，部分遥感卫星在轨利用余弦曲线对偏流角进行拟合以减少计算量，但误差较大；有的卫星偏流角由有效载荷负责计算，卫星平台实现跟踪。本文根据偏流角产生的机理，用轨道要素法推导了一种简化的偏流角计算与补偿方法，其特点是计算量小、精度高，并在此基础上分析了不对偏流角进行控制时偏流角对品字形拼接探测器成像的影响。

1 偏流角定义与计算

空间相机在对地成像过程中，因卫星轨道运动、地球自转和飞行器姿态等因素综合影响，使卫星飞行方向与地面像点移动方向存在一夹角，称此为偏流角[6-7]。偏流角会对成像质量造成显著影响，高精度成像时必须对偏流角进行补偿。

卫星在轨飞行中，仅考虑地球自转的卫星升轨偏流角如图1所示。

(1)

式中：

此处：ω为卫星轨道角速度；R为卫星向径；i为卫星轨道倾角；ωe为地球自转角速度；δ为卫星星下点纬度。

式(1)可变为

(2)

同理，降轨时偏流角为正，有

(3)

可利用卫星的纬度幅角将升降轨的偏流角计算统一表示，考虑符号，有计算公式

(4)

式中：δ=arcsin(sini·sinu)；γ=arccos(tanδ·cotu)。此处：u为卫星纬度幅角。

若某卫星轨道为圆轨道，半长轴7 076 km，轨道倾角98.2°，可算得卫星过赤道时的偏流角最大，3.855°。一轨内不同卫星纬度幅角和星下点纬度的偏流角分别如图2、3所示。

用坐标转换或随体导数的方法可对偏流角进行严格计算[8-9]。可知卫星的滚动侧摆角越大，偏流角就越小，滚动角20°时偏流角减小约0.2°；卫星俯仰角越大，偏流角亦越大，俯仰角20°时偏流角增大约0.3°；偏航角与偏流角的大小直接相关。仅考虑姿态角速度时，卫星偏流角对滚动角速度的影响最敏感，俯仰角速度次之，偏航角速度基本无影响。当三轴角速度均为0.001 (°)/s时，滚动角速度的影响约0.1°，俯仰角速度的影响0.007°，偏航角速度的影响0.004°。实际上，遥感卫星的指向精度常优于0.1°，指向稳定度常优于0.001 (°)/s。姿态角及姿态角速度对偏流角的影响优于0.1°，优于多数卫星的指向精度，一般情况下可忽略姿态及姿态角速度的影响。

2 偏流角补偿方法

偏流角算出后，需通过卫星的姿态控制系统实现补偿控制。一般偏流角在卫星的本体坐标系中计算，则偏流角补偿前后的姿态矩阵Aob，A′ob满足关系

(5)

式中：Rz(β)为绕Z轴转动β的旋转矩阵，且

当欧拉角解算转序为1-2-3时，偏流角补偿前后成立

(6)

式中：ψ，θ，φ为欧拉角，定义为特定转序的3个欧拉转角，绕X轴转动的角度为滚动角φ，绕Y轴转动的角度为俯仰角θ，绕Z轴转动的角度为偏航角ψ；Rz(ψ)，Ry(θ)，Rx(φ)分别为绕Z轴转动ψ、绕Y轴转动θ、绕X轴转动φ的旋转矩阵，且

由式(6)可知：只要最后一个转序方向为Z轴，根据矩阵乘法的合成原理，偏流角可直接加上偏航角接入系统闭环，即2-1-3转序也可直接加上偏航角接入系统闭环。

目前，卫星常用的欧拉角转序为3-1-2，此时偏流角补偿前后有

(7)

因Rz(β)Ry(θ)Rx(φ)Rz(ψ)不等价于Ry(θ)Rx(φ)×Rz(ψ+β)，需将新姿态矩阵重新分配到3-1-2转序的欧拉角，用方向余弦矩阵重新解算的欧拉角为

式中：A′ij为偏流角补偿后的姿态矩阵A′ob中的对应第i行第j列元素。φ′，θ′，ψ′即为重新解算的欧拉角，可作为控制目标代入闭环进行控制。用重新解算欧拉角方法，可规避三轴欧拉姿态角的转序影响，保证卫星控制软件的继承性，减少软件编制与测试的工作量。

3 偏流角对品字形拼接探测器成像影响

从像元错位影响、MTF、通道间配准精度、幅宽，分析偏流角对品字形拼接探测器成像的影响。假设品字形探测器两排探测器同一谱段间的距离为l，探测器重叠距离为s，像元尺寸为d，TDI积分级数为n。

3.1 像元错位影响

3.1.1 穿轨横向像元错位

已知偏流角为β，则横向错位像元数

(8)

在卫星探测器间距4.94 mm，像元尺寸30 μm，卫星姿态角和姿态角速度为零时，卫星不同纬度时的错位像元数如图4所示。

由图4可知：在穿轨方向，不同的偏流角可造成双排探测器对同一条带成像时的穿轨方向错位像元数随纬度发生变化，从赤道到两极，空间错位量从11.1像元连续变化至无错位。优化地面图像拼接算法可将像元错位影响影响降至最低，但缺点是增加了图像拼接配准难度。为避免出现漏扫，要求相邻探测器重叠像元数不能少于12个。对偏流角进行控制后，可消除穿轨像元的错位。

3.1.2 沿轨纵向像元错位

在沿轨方向，由于地球自转线速度在该方向存在分量，其值在赤道最大，两极最小，从而引起不同纬度地区两排探测器对同一地物条带成像存在时间差。令成像空间分辨率为s，地球赤道线速度为ve，卫星星下点速度为vs，则两排探测器成像时间差

(9)

在卫星探测器间距4.94 mm，像元尺寸30 μm，轨道倾角98.203°时，可算得Δt为0.732～0.738 s，相当于像元错位数为0.23～1.62。沿轨方向的像元错位影响不能通过偏流角控制消除。已知该卫星每个像元的积分时间4.4 ms，则可计算卫星过不同纬度的纵向像元错位数，结果如图5所示。

纵向像元错位是品字形拼接探测器固有特性，采用偏流角控制也不能消除，但其影响可通过后期像元配准改善。

3.2 MTF影响

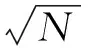
MTF的值LMTF与积分级数、像元尺寸等因素相关，有

(10)

式中：N为积分级数；f为空间频率，取奈奎斯特频率fN=0.5/d；Δb为像移距离[11]。此处：d为像元尺寸。

3.2.1 穿轨方向MTF

在穿轨方向，将Δb=dsinβ，fN代入式(10)可得

(11)

由式(11)可知：穿轨方向的MTF只与偏流角的大小及积分级数有关，与像元尺寸无关。

由图2偏流角计算结果，12，24，48，96级积分时的穿轨MTF如图6所示。

由图6可知：12级积分时，偏流角对MTF的影响最大为0.75；24级积分时，对MTF的影响最大为0.21；48，96级积分时，MTF均为零。对偏流角进行控制后，穿轨MTF的影响可消除。

3.2.2 沿轨方向MTF

在沿轨方向，将Δb=d(1-cosβ)，fN=代入式(10)可得

(12)

由式(12)可知：沿轨方向的MTF与像元尺寸无关，只与偏流角及积分级数相关。

由图2偏流角计算结果，12，24，48，96级积分时的沿轨MTF如图7所示。

由图7可知：偏流角对沿轨MTF的影响很小，当积分级数为最大96级时，偏流角对MTF的最大影响程度为0.98。对偏流角进行控制后，沿轨

MTF的影响可消除。

3.3 通道间配准精度影响

随着遥感技术的发展，空间相机的探测波段逐渐增加，多光谱遥感技术已成为高精度对地遥感的主流技术，对多通道间的配准精度提出了新要求。不同谱段在焦平面上一般在沿轨方向错开，进行品字形拼接后，前后两排探测器间不同谱段间的间距不再一致，导致多个谱段的图像配准出现困难。

通道间配准精度影响分析与像元错位影响分析类似，令l为前后两排探测器不同谱段间的距离，则通道间错位像元数

(13)

某卫星短中波红外品字形焦平面组件中有短中波红外谱段4个，短波像元尺寸d=20 μm，中波像元尺寸d=40 μm，不同谱段间距MW2-MW1为1.12 mm；MW2-SW2为2.76 mm；MW2-SW1为4.14 mm；MW1-SW2为1.64 mm；MW1-SW1为3.02 mm；SW2-SW1为1.38 mm，则可算得不同纬度时短中波红外通道间像元错位数见表1。

某卫星的长波红外品字形焦平面组件有长波红外谱段4个，像元尺寸d=40 μm，已知不同谱段间距LW4-LW3为1.12 mm；LW4-LW2为2.76 mm；LW4-LW1为3.88 mm；LW3-LW2为1.64 mm；LW3-LW1为2.76 mm；LW2-LW1为1.12 mm，则可算得不同纬度时长波红外通道间像元错位数见表2。

由表1、2可知：由于偏流角的影响，在纬度0°～80°间，短中波红外焦平面组件最大像元错位数为13.92，相当于至少14个像元的错位，从第15个像元开始能重叠；长波红外焦平面最大像元错位数为6.53，相当于至少7个像元的错位，从第8个像元开始能重叠。一般配准精度指标要求小于0.5个像元，如不进行偏流角校正，将会严重降低通道间配准精度，影响数据的使用。

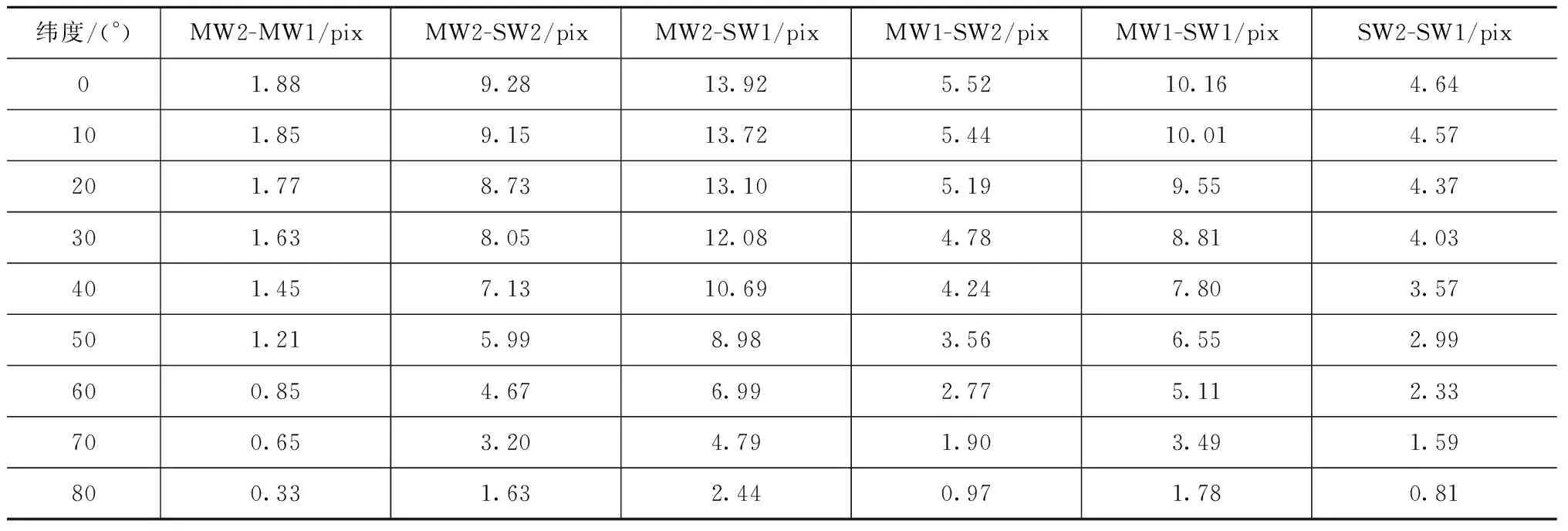
表1 不同纬度下短中波红外通道间像元错位Tab.1 Malposition of SWIR/MWIR pixels with different latitude

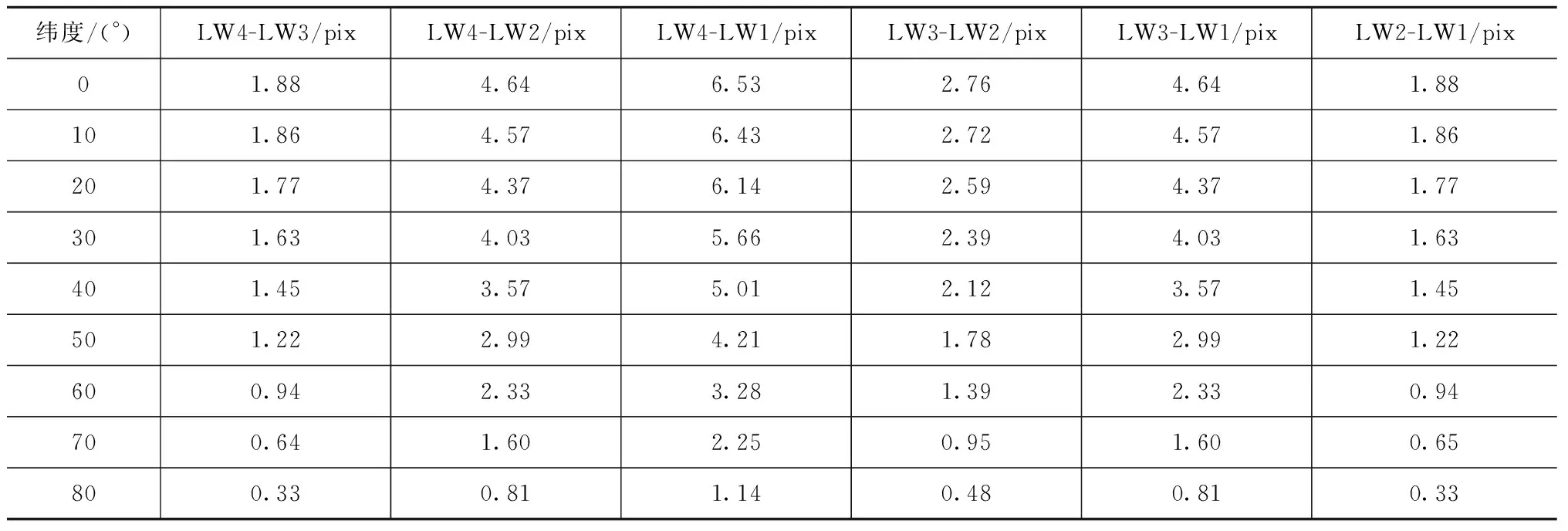
表2 不同纬度下长波红外通道间像元错位Tab.2 Malposition of LWIR pixels with different latitude

3.4 幅宽影响

不对偏流角进行校正时，幅宽受两个因素的影响：一是探测器的实际推扫方向与探测器的穿轨方向不垂直，相当于倾斜了偏流角大小的角度进行推扫，存在幅宽损失；二是像元错位及重叠像元数设计导致探测器实际可用元数减少，造成幅宽损失。

3.4.1 倾斜推扫损失

若设计幅宽为W，则实际幅宽

(14)

当W= 60 km时，可得W′=59.86 km。

3.4.2 像元错位损失

不对偏流角进行校正时，同一通道的幅宽拼接可通过提高相邻探测器模块的重叠像元数解决，但不同通道间的幅宽配准需考虑通道间像元配准的影响。令每块探测器的穿轨像元数为n，探测器模块数为k，相邻探测器的重叠像元数为i，每个探测器代表的地面像元分辨率为s，最大像元错位数为m，则有

(15)

取表1的通道间配准精度结果，短中波红外焦平面最大通道间错位像元数为13.92。该焦平面每个探测器模块短波红外为1 024元，中波红外为512元，相邻探测器的重叠像元数短波红外为48元，中波红外为24元，共采用3块探测器进行拼接，每个像元对应的空间分辨率短波红外为20 m，中波红外为40 m，由式(15)可得W′=57.84 km。

取表2的通道间配准精度结果，长波红外焦平面最大通道间错位像元数为6.53元。该焦平面每个探测器模块为512元，相邻探测器的重叠像元数为24元，共采用3块探测器进行拼接，每个像元对应的空间分辨率为40 m，由式(15)可得有W′=57.84 km。

综合上述分析，偏流角主要通过影响像元错位而影响实际幅宽。对偏流角进行校正后，偏流角不会影响品字形探测器通道间的配准精度，从而不影响幅宽。

4 结束语

随着高分辨率遥感卫星的发展，有越来越多的卫星采用了偏流角补偿功能。本文根据偏流角产生的机理，用轨道要素法推导了一种简化的偏流角计算与补偿方法，并分析了不对偏流角进行控制时偏流角对品字形拼接探测器成像的影响。研究表明：根据偏流角产生的机理，以纯轨道要素作为输入，推导了一种精度高、计算量小的偏流角计算方法，不会显著增加星上计算量，不存在计算发散或迭代不收敛问题，可进行在轨推广应用；给出了一种不改变常规3-1-2欧拉姿态角转序的偏流角补偿方法，可大幅借鉴不进行偏流角补偿的卫星控制软件模块，能显著减少软件代码编制及测试工作；分析了不进行偏流角补偿控制时，偏流角对品字形拼接探测器的像元错位、MTF、通道间配准精度和幅宽的影响，可作为卫星总体分析及是否考虑增加偏流角补偿功能的判断依据。本文的偏流角计算方法存在对大角度姿态机动时误差较大的缺点，但能通过增加机动偏流角补偿算法，减少机动时的补偿误差。如后续星上计算量允许，也可考虑直接利用矢量运算法，进行大角度姿态机动的偏流角计算。

[1] 曲宏松, 金光, 张叶. “NextView 计划”与光学遥感卫星的发展趋势[J]. 中国光学与应用光学, 2009, 12(6): 468.

[2] 田国良. 我国遥感应用现状、问题与建议[J]. 遥感信息, 2003(2): 2-5.

[3] 杨桦, 郭悦, 伏瑞敏. TDICCD的视场拼接[J]. 光学技术, 2003, 29(2): 226.

[4] 张星祥, 任建岳. TDICCD焦平面的机械交错拼接[J]. 光学学报, 2006, 26(5): 740-745.

[5] 岳庆兴, 邱振戈, 贾永红. TDI CCD相机动态成像对

几何质量的影响分析[J]. 测绘科学, 2012, 37(3): 14.

[6] 陈黎， 翟林培， 李友一. 基于航空遥感器像移补偿实现方法的研究[J]. 计算机测量与控制, 2009, 17(1): 154-155.

[7] 陈梁， 刘春霞， 龚惠兴. 极轨星载TDICCD相机的像移及恢复算法研究[J]. 遥感学报, 2002, 6(1): 35-36.

[8] 张大伟， 温渊， 薛孝补， 等. 卫星偏流角的矢量计算方法研究[J]. 上海航天, 2016, 33(3): 11-16.

[9] 李伟雄， 徐抒岩， 闫得杰. 影响空间相机偏流角估值误差的参数[J]. 红外与激光工程, 2011, 40(8): 1530-1537.

[10] 朱兴鸿, 邸国栋, 陆春玲. 一种遥感卫星偏流角修正的仿真分析方法[J]. 航天器工程, 2013， 22(1): 39-43.

[11] 樊超, 李英才, 易红伟. 空间相机中的偏流角分析[J]. 红外与激光工程, 2006, 35(S2): 216-220.

Drift Angle Compensation Study of Interleaving Assembly Focal Plane

WEN Yuan, ZHANG Da-wei

(Shanghai Institute of Satellite Engineering, Shanghai 201109, China)

The drift angle compensation of interleaving assembly focal plane for TDI-CCD scanning in remote sensing satellite was studied in this paper. A simple and reliable method of computation and compensation of drift angle was given by orbit elements method. The Euler angle calculated after the drift angle had been compensated was used as the control target to input into closed loop for control, which could avoid the influence of the turn order of three Euler angle. The influences of drift angle compensation on pixel malposition, modified transfer function, registration and swath were analyzed. It was found that the pixel malposition in cross-track could be eliminated, the pixel malposition in along-track could not be eliminated, MTF in cross-track and along-track could both be eliminated, and the drift angle had no influence on swath after the drift angle compensated. And it was also found that the registration accuracy would be affected seriously if the drift angle had not be compensated. The method proposed was simple and clear which was valuable in engineering.

remote sensing satellite; TDI-CCD scanning; drift angle; interleaving assembly; compensation; pixel malposition; modified transfer function; registration; swath

1006-1630(2017)02-0127-07

2016-07-25；

2016-09-27

温 渊(1987—)，男，硕士，主要研究方向为卫星轨道、姿态动力学与控制及卫星总体设计。

V445.8

A

10.19328/j.cnki.1006-1630.2017.02.014