基于并行技术和流水线的LMS自适应滤波算法*

杜秀丽 江焕承 陈 波 邱少明

(1.大连大学通信与网络重点实验室，大连，116622；2.大连大学信息工程学院，大连，116622)

基于并行技术和流水线的LMS自适应滤波算法*

杜秀丽1,2江焕承2陈 波1,2邱少明1,2

(1.大连大学通信与网络重点实验室，大连，116622；2.大连大学信息工程学院，大连，116622)

针对现有自适应滤波算法中数据处理效率低的问题，提出了基于并行技术和流水线的最小均方误差(Least mean square,LMS)自适应滤波算法。该算法构建基于并行技术的多输入多输出滤波器结构，成倍提高系统滤波处理速度；设计基于流水线的LMS自适应滤波权系数求解方法，有效改善了权系数计算效率。最后利用现场可编程门阵列(Field programmable gate array,FPGA)对该算法进行了验证，结果表明，对于四级并行流水线四阶LMS自适应滤波器，其数据处理速率提高了约8倍，在相同的数据处理速率下，其功耗可降低约84%，从而提高了LMS自适应滤波处理速率，降低了系统功耗，实现了高速、超高速数据流的实时自适应滤波处理。

自适应滤波；并行技术；最小均方误差；流水线

引 言

自适应滤波算法广泛应用于图像处理、雷达成像、仪器仪表以及自适应控制等领域。随着数字信号处理技术的快速发展，数据处理速率也越来越高，传统的自适应滤波算法已不能满足现代数字信号处理中高速性、实时性的要求，如何实现高速数据流的实时自适应滤波已成为制约高速数据滤波发展的重要因素，因此研究高速信号的自适应滤波算法不仅具有重要的理论意义，更有利于自适应滤波技术在高速数据处理领域的发展与应用。

典型的自适应滤波算法主要有递归最小二乘(Recursive least square,RLS)算法[1]和最小均方误差(Least mean square,LMS) 算法[2]等。高斯提出的RLS自适应滤波算法具有较好的收敛性能和稳定性，但是以增加计算复杂度和降低系统稳定性为代价，因此难以应用于高速信号处理；Widrow和Hoff提出的LMS自适应滤波算法因其实现简单、鲁棒性好、对信号统计特性变化具有稳健性等特点，被广泛应用于自适应滤波领域。文献[3,4]提出了适用于电子信号处理(Digital signal processing,DSP)的LMS算法，该算法主要应用于低速信号的自适应滤波处理；文献[5,6]介绍了适用于软件实现的LMS算法，其算法实现复杂度较高，计算量较大，无法实现高速信号的自适应滤波；文献[7,8]提出了基于现场可编程门阵列(Field programmable gate array,FPGA)的LMS算法，将现有的LMS算法进行了改进，使其适用于FPGA实现，使得自适应滤波速率得到了进一步的提升，但由于滤波器结构及其参数计算算法的复杂性，使其仍难以满足高速信号的自适应滤波处理。基于此，本文提出了一种基于并行技术和流水线相结合的LMS自适应滤波算法。与现有基于FPGA的LMS自适应滤波算法相比，该算法改善了现有自适应滤波结构效率低的问题，克服了权系数计算速率慢的缺点，满足了高速数据流的实时自适应滤波处理。

1 LMS自适应滤波算法

图1 LMS自适应滤波算法结构Fig.1 Traditional LMS adaptive filtering structure

LMS算法是一种线性自适应滤波算法，其通过自行调整滤波器权系数, 使滤波器的输出信号与期望输出信号之间的均方误差最小，其原理如图1所示。主要包含两个基本过程[9](1)滤波过程：计算线性滤波器输出对输入信号的响应。(2)自适应过程：(a)通过比较输出结果与期望响应产生估计误差；(b)根据估计误差自动调整滤波器权系数。

基本LMS算法的迭代公式为

(1)

(2)

(3)

式中：y(n)为滤波器输出信号；w(n)为自适应滤波器在时刻n的权向量;x(n)为时刻n的输入信号向量；e(n)为误差信号；d(n)为期望信号；式(3)表示抽头权向量更新公式，μ为控制收敛速度的常数，其为步长因子。LMS算法收敛的条件为：0<μ<1/Kmax，Kmax为输入信号自相关矩阵的最大特征值。

2 基于并行技术和流水线的LMS自适应滤波结构

针对现有LMS自适应滤波算法中滤波器单输入单输出结构数据处理速率较慢的问题，将并行技术应用到滤波器结构中，实现并行多输入多输出滤波结构，提升数据处理速率；同时将流水线技术应用于LMS自适应滤波算法权系数求解方法，可以提高滤波器工作频率。

2.1 基于并行技术的LMS自适应滤波结构

并行处理[10-11]涉及系统体系结构、算法映射、布局布线和程序设计等多项技术。利用计算中运算数据的并发性，在并行处理中将多个输入数据在一个时钟周期内并行地计算，从而使数据处理速率提升为并行级数相当的倍数。并行处理结构也能用于降低系统功耗。

对于现有LMS自适应滤波器结构，其FPGA实现的传播延时Tseq与其关键路径上各种MOS管栅极和杂散电容的充放电荷密切相关[8]，传播延时(即系统最小时钟周期)的计算公式为

(4)

式中：Ccharge表示在单个时钟周期里充放电的电容；V0为电源电压；Vt为阈值电压；k为工艺参数。其功耗为

(5)

式中：f= 1/Tseq。

现有LMS自适应滤波结构是一种单输入单输出(Single input single output,SISO)系统，运用并行处理技术可以将SISO系统变换为L通道并行多输入多输出(Multiple input multiple output,MIMO)系统，对于L通道并行MIMO系统，其处理过程关键路径保持不变, 但在相同的时间里处理的数据量是原来的L倍，相当于数据处理速率提升为原来的L倍。这样，系统有效处理速率提高到与并行级数相当的L倍。

并行处理技术可以通过降低电源电压来降低功耗，在一个L通道并行MIMO系统中，关键路径充放电电容保持不变，在相同数据处理速率下，L通道并行MIMO系统电路的时钟周期增加到LTseq，则其充电电压可降低为βV0(0<β<1)。L通道并行MIMO系统的功耗Ppar可降低为现有LMS自适应滤波结构功率Pseq的β2(0<β<1)倍，即

(6)

图2 四通道并行MIMO LMS自适应滤波结构Fig.2 LMS filter structure based on four channels

L通道并行MIMO系统传播延时为

(7)

在相同数据处理速率下，功耗系数β(0<β<1)可由式(4)，(7)导出。

对于四阶LMS自适应滤波器，本文以四通道并行MIMO系统为例分析。在相同时钟频率下，其数据处理速率提高为原数据处理速率的4倍；在相同数据处理速率下，其功耗降低为原功耗的β2倍，其结构实现如图2所示。

2.2 基于流水线的权系数求解方法

Merlino提出的流水线技术[10,12]是一种在单时钟周期进行多指令运算的处理技术。流水线可以大幅缩短数据处理关键路径延时，从而可提高滤波器工作频率和数据处理速率，或在同样工作频率下降低系统功耗。流水线通过沿着数据运算通路插入流水线寄存器的方法来减小关键路径延时。加入M级流水线后，滤波器工作频率可近似提高M倍。对于M级流水线系统, 其关键路径近似缩短为原始路径长度的1/M，单级流水线充放电电容减小为Ccharge/M，总电容并没有变化。如果时钟频率f保持不变，在原来对电容Ccharge充放电的同样时间内，现在只需要对Ccharge/M进行充放电。这意味着，电源电压可以降低到β′V0。这样加入M级流水线滤波器的传播延时为

(8)

功耗为

(9)

因此，流水线系统的功耗降低为原来的β′2倍。在相同时钟速率下，可得传播延时Tseq=Tpip，从而由式(4，9)求得β′(0<β′<1)。

图3为加入四级流水线的LMS自适应滤波权系数求解结构。加入流水线的权系数求解结构改进了误差函数e′(n)求解方法，运用4组误差值的平均值作为误差函数，提升了误差函数计算的稳定性，从而提高了自适应滤波算法的稳定性，改进后的权系数求解公式为

(10)

(11)

如图3所示，通过加入四级流水线，其关键路径近似变为原多项结构的1/4，滤波器工作频率可提高为原工作频率的4倍；在相同工作频率下，其功耗可降低为原功耗的β′2(0<β′<1)倍。

图3 四级流水线LMS自适应滤波权系数求解方法Fig.3 LMS filter coefficient based on 4 stages pipelines

图4 系统处理速率及功耗与流水线级数关系Fig.4 Relationship between pipeline stages and system frequency, power consumption

综上所述，加入并行技术和流水线的LMS自适应滤波算法，可大幅提高现有LMS自适应滤波处理速率，从而提高有效实现高速数据流的实时自适应滤波处理。

3 FPGA实现及仿真验证

分别对加入流水线的权系数求解结构最小时钟周期、功耗与流水线级数的关系进行仿真，结果如图4所示。由图4可知对于四阶LMS自适应滤波权系数求解结构而言(流水线级数为0级时即为现有自适应滤波器)，当流水线级数小于等于4级时，其最小时钟周期与功耗均随流水线级数增加而减小，系统时钟速率提升，功耗下降；当流水线级数大于4时，由于系统最小延时即为乘法器延时，因此其最小时钟周期保持不变，随着流水线级数的增加，其引入的延迟单元不断增多，系统功耗逐渐增大。综上所述对于四阶LMS自适应滤波权系数求解结构，其流水线级数为4时，系统数据处理速率最快，功耗最低，系统最优。

基于并行技术和流水线的LMS自适应滤波算法的FPGA实现，本文采用xilinx FPGA的Virtex5开发平台,运用Xilinx FPGA集成开发环境Xilinx ISE Design Suite 12.1进行代码的设计、编译、仿真以及在线验证，并将其应用于100M以太网信号自适应滤波处理。

表1对现有LMS自适应滤波算法与4级并行流水线LMS自适应滤波算法在设计实现时的硬件资源消耗、系统关键路径以及功耗等方面进行对比分析。 由表1可知，引入了4级并行MIMO结构与4级流水线技术，虽然使用了较多的硬件资源，但却大幅缩短了系统关键路径，使得自适应滤波器工作频率可提高为原工作频率的(2TM+4TA)/TM倍(TM为乘法器延时，TA为加法器延时)，从而可大幅提高LMS自适应滤波处理速率，降低系统功耗。

对100 MB以太网信号的自适应滤波测试，将改进前后的自适应滤波处理算法在FPGA中实现。通过测试可知，改进后的数据处理速率由原有的40 MB/s提升到190 MB/s，使得数据处理速率得到大幅提升，功耗提升了84%，从而有效降低处理系统功耗。

表1 改进前后消耗资源对比

运用FPGA在线调试工具Chipscope Analyzer进行在线测试，图5为现有LMS自适应滤波结构测试结果，图6为4通道并行LMS自适应滤波结构测试结果，由图5,6的对比可知，对于加入并行技术的4通道并行LMS自适应滤波结构， 其数据处理方式由传统的单路实现提升为4路实现，数据输入输出从单输入输出提升为4通道并行输入并行输出，从而大幅提升了数据处理效率，在相同系统时钟速率下，4通道并行LMS自适应滤波算法滤波速率是现有LMS自适应滤波算法的4倍。

图5 现有LMS自适应滤波算法输入输出Fig．5 The in/out of traditional LMS filtering structure

图6 4通道并行LMS自适应滤波算法输入输出Fig.6 The in/out of 4-channel parallel LMS filtering system

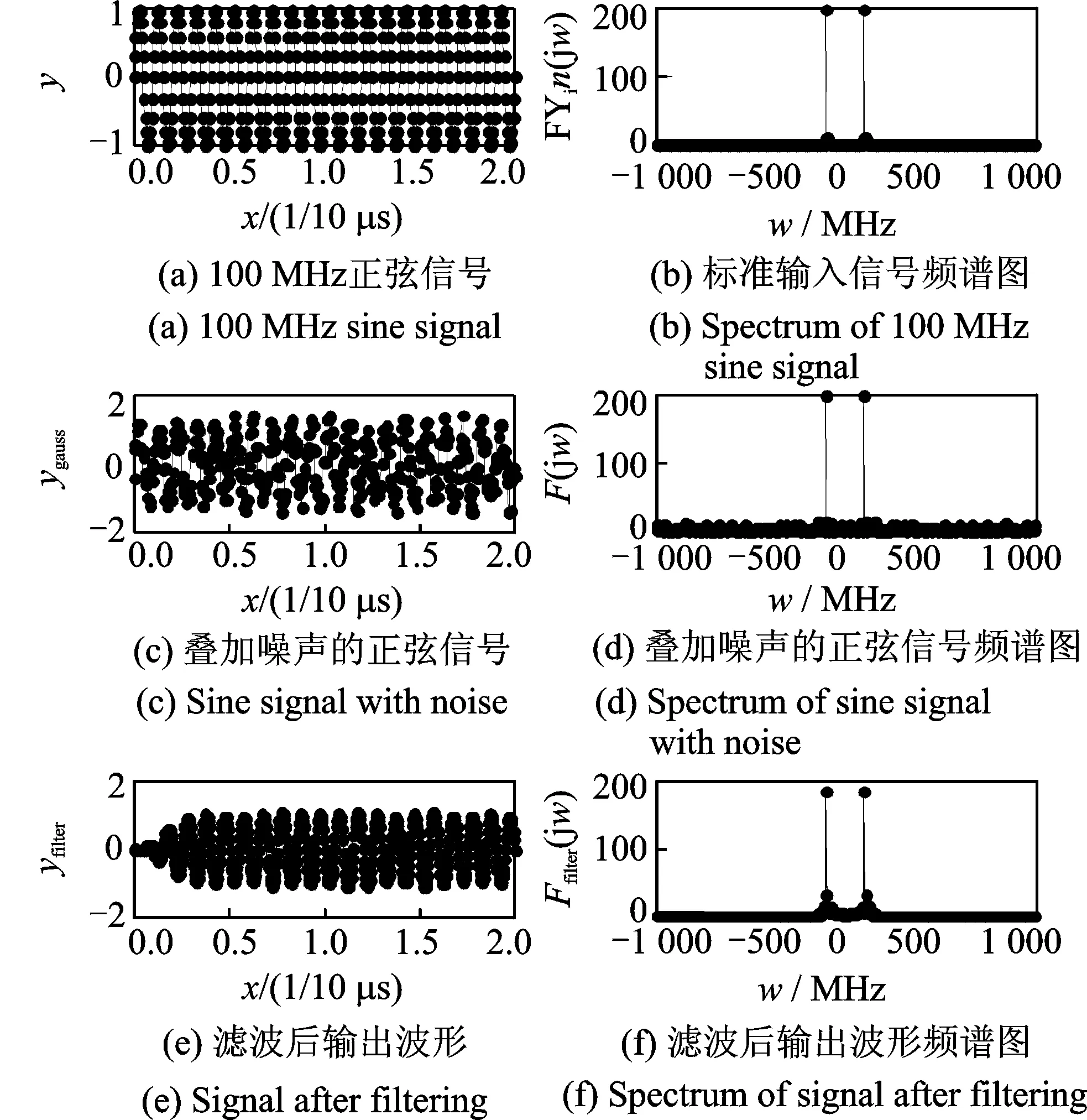
图7 滤波前后时域频域分析 Fig.7 Time and frequency domain analysis before and after filtering

图7为4级并行流水线LMS自适应滤波结构滤波前后对比仿真。如图所示，标准信号为100 MHz的正弦信号，采样率为2 000 MHz；滤波器输入信号为加入期望为0，方差为0.25的高斯白噪声的标准信号。由时域、频域对比可知，该系统可很好地滤除信号中加入的白噪声，在提升系统处理速度、降低功耗的同时有效地实现了噪声的滤除。

综上分析，运用流水线和并行技术，使得改进后自适应滤波工作频率提升为传统自适应滤波的(2TM+4TA)TM倍，功耗降低为传统LMS自适应滤波算法的15.79%，从而大幅提高了数据处理速度，有效降低了系统功耗，实现了高速、超高速数据流的实时自适应滤波处理。

4 结束语

本文研究了高速数据LMS滤波算法、流水线和并行技术，将流水线和并行技术应用于LMS自适应滤波算法，提出了一种基于并行技术和流水线的最小均方误差( LMS)自适应滤波算法的实现结构。该结构改善了现有自适应滤波结构效率低的问题，克服了权系数计算速率慢的缺点，大幅提高了数据处理速率；在相同的数据处理速率下，其功耗可降低约84%；最后通过FPGA实现了基于并行流水线LMS自适应滤波算法。仿真实验表明，该算法虽然使用了较多的硬件资源，但却大幅提高了数据处理速度，有效降低了系统功耗，可用于高速数据流的实时自适应滤波处理。

[1] 周直, 唐斌, 祝俊. 宽带数字信道化并行结构及FPGA实现[J].数据采集与处理,2010,25(5):661-665.

Zhou Zhi, Tang Bin, Zhu Jun. Wideband digital channelized parallel architecture and its FPGA implementation[J]. Journal of Data Acquisition and Processing,2010,25(5):661-665.

[2] 赵秋领, 冯立辉, 赵克, 等. LMS 算法在微石英音叉陀螺信号解调中的应用[J]. 仪器仪表学报,2013,34(2): 366-370.

Zhao Qiuling, Feng Lihui, Zhao Ke, et al. Application of LMS algorithm in signal demodulation of micro-quartz tuning gyroscope[J]. Chinese Journal of Scientific Instrument, 2013,34 (2): 366-370.

[3] Zhou Jianjun, Lin Chunsheng, Chen Hao. A method for aircraft magnetic interference compensation based on small signal model and LMS algorithm[J]. Chinese Journal of Aeronautics, 2014, 27(6): 1578-1585.

[4] 徐艳红. 基于模糊LMS算法的自适应噪声消除器[J]. 数据采集与处理, 2012,27(S1): 66-69.

Xu Yanhong. Adaptive noise canceller based on fuzzy LMS algorithm[J]. Journal of Data Acquisition and Processing, 2012,27(S1): 66-69.

[5] 陈 琳, 李建勋, 戴虎,等. 自适应滤波在动态推力测量中的应用[J]. 宇航学报, 2010, 7(31):1819-1824.

Chen Lin, Li Jianxun, Dai Hu, et al. Application of adaptive filter in dynamic thrust measurement[J]. Journal of Astronautics, 2010, 7(31):1819-1824.

[6] 任自钊, 徐建城, 闫永鹏. 一种改进的变步长 LMS自适应滤波算法及性能分析[J]. 计算机应用研究, 2011, 3(28): 954-956.

Ren Zizhao, Xu Jiancheng, Yan Yongpeng. Improved variable step size LMS adaptive filtering algorithm and its performance analysis [J]. Application Research of Computers, 2011, 3(28): 954-956.

[7] 付学志, 刘忠, 胡生亮, 等. 基于FPGA的改进型最小均方自适应时延估计器[J]. 系统工程与电子技术, 2011, 33(5):1191-1196.

Fu Xuezhi, Liu Zhong, Hu Shengliang, et al. Improved LMS adaptive time delay estimator based on FPGA [J]. Systems Engineering and Electronics, 2011, 33(5):1191-1196.

[8] Borisagar K R, Sedani B S, Kulkami G R. Simulation and performance analysis of LMS and NLMS adaptive filters in non-stationary noisy environment[J]. Gwalior, 2011, 6(10):32-35.

[9] 高金定. 平稳环境下LMS算法优化分析及其FPGA实现[J]. 压电与声光, 2013,35(3):445-451.

Gao Jinding. Optimization analysis of LMS algorithm in stationary environment and its FPGA implementation [J]. Piezoelectrics &Acoustooptics, 2013,35(3):445- 451.

[10]Polpo A, Pereira C. Reliability nonparametric Bayesian estimation in parallel system [J]. IEEE Trans on Reliability, 2009, 58(2): 364-373.

[11]邓军, 杨银堂. 全数字接收机中一种基于并行流水线与快速 FIR算法的插值滤波器结构及其实现[J]. 电子与信息学报, 2010, 32(9):2089-2094.

Deng Jun, Yang Yintang. Structure of interpolation filter based on parallel pipelining and fast FIR algorithm and its implementation for all digital receiver[J]. Journal of Electronics & Information Technology, 2010, 32(9):2089-2094.

[12]Merlino P, Abramo A. A fully pipelined architecture for the LOCO-I compression algorithm [J]. IEEE Trans on Very Large Scale Integration (VLSI) Systems, 2009, 17(7): 967-971.

LMS Adaptive Filter Algorithm Based on Parallelism and Pipeline

Du Xiuli1,2, Jiang Huancheng2, Chen Bo1,2, Qiu Shaoming1,2

(1.Key Laboratory of Communication and Network, Dalian University, Dalian, 116622, China； 2.College of Information Engineering, Dalian University, Dalian, 116622, China)

To increase low efficiency of handling high-speed data in existing adaptive filter algorithms, an least mean squarse(LMS) adaptive filter algorithm based on parallel technology and pipeline is proposed. The proposed algorithm accelerates data processing speed to improve the speed of weight coefficient computing significantly, and reduces the critical path to improve the system working clock effectively. In the experiment based on FPGA, for the LMS adaptive filter based on 4-channel parallel structure and 4-stage pipelines, its data processing rate increases by eight times, and the power consumption can be reduced to 16%, with the same rate of data processing. It can thus realize the real-time LMS adaptive filtering process of high-speed or hyper-speed data stream.

adaptive filtering; parallelism; least mean squares(LMS); pipeline

国家高技术研究发展计划(“八六三”计划)(2014AAXX10E)资助项目；辽宁省教育厅科学技术研究项目(L2014495)资助项目。

2015-02-07；

2015-05-18

TP274.2

A

杜秀丽(1977-)，女，教授，研究方向：现代数字信号处理，E-mail: dxlxts@126.com。

邱少明(1977-)，男，副教授，研究方向：信号采集与滤波。

江焕承(1990-)，男，硕士研究生，研究方向：信号滤波技术。

陈波(1972-)，男，教授，研究方向：高速信号处理。