浅谈定性分析的物理教学价值

朱佳平 沈金林

(1. 余杭实验中学,浙江 杭州 311100; 2. 浙江省平湖中学,浙江 平湖 314200)

浅谈定性分析的物理教学价值

朱佳平1沈金林2

(1. 余杭实验中学,浙江 杭州 311100; 2. 浙江省平湖中学,浙江 平湖 314200)

定性分析与定量分析是两种科学分析方法.由于物理科学的高度定量化,使得在物理教与学的过程中,师生都有重定量轻定性的偏向.本文主要论述了定性分析作为一种处理物理问题的重要科学方法在教材中的体现,及其应用于处理物理问题的价值,并结合实例阐述了高中物理教学中进行定性分析的8种方法.

定性分析;物理教学;教学价值

物理学是一门高度定量化的科学,其测量之精确、逻辑推理之严密、模型建立之完善,并取得了巨大的成就,这也使得“定性”有时成了带贬义的意思.卢瑟福有句名言:“定性就是定量化不够”.许多教师在物理教学中也存在“重定量,轻定性”的偏向,总认为定量是优越的,定性是不得已而为之,只有精确的定量才是最终的追求.以至于“物理知识=物理公式=数学运算”在学生中成为一种普遍意识,许多学生形成了这样的思维习惯:一拿到物理问题就是寻找公式,进行数学演算.

其实,定性分析作为一种科学方法,在物理科学中发挥着重大作用,在物理教学中具有重要的教育价值.尤其在核心素养视域下,定性分析中的许多思维方法作为高阶位的思维品质,是学生适应个人终身学习和社会发展的基本素养,能为学生终身受用.本文试结合对定性分析的思考和认识,谈谈高中物理教学中定性分析的教育价值.

1 关于定性分析和定量分析

所谓定性分析就是对事物进行“质”的方面的分析,具体地说是主要凭分析者的直觉、经验,运用归纳和演绎等方法,对事物的性质、特点、规律等作出判断的一种方法.如伽利略用演绎法推翻亚里士多德的“重物比轻物落得快”的论断就是定性分析应用的典范.

所谓定量分析就是对事物进行“量”的方面的分析,具体地说是依据数据,建立数学模型,并用数学模型计算出事物的各项指标及其数值的一种方法.如开普勒依据第谷大量的行星观测数据,历经20年的尝试性定量计算,最终得出行星运动三定律.

定性分析和定量分析作为人们认识事物的两种科学分析方法,各有其侧重,但在真实的科学研究中它们又是彼此交融的.以近代科学方法的开创者伽利略对自由落体运动的研究为例,其探究过程可概括为如图1所示.分析其中的基本要素可以发现,科学探究首先需要对现象进行观察,进而提出假设.而“提出假设”是科学探究中最活跃、最具革命性的要素,“提出假设”需要定性分析、归纳,甚至是基于直觉思维,没有足够的定性分析,提出的假设将是盲目的、无意义的.因此,定性分析是科学研究过程的良好开端和重要环节.伽利略的成功,不仅在于找到了落体运动的规律,更重要的是开辟了一条研究物理学的研究之路——运用数学推理和实验研究相结合探究自然规律的科学方法,即定性与定量相结合的方法.

图1

学生分析解决物理问题的思维过程与物理学家的科学探究过程不无相通之处,如缺乏对物理问题的定性分析和整体把握,一下子陷入细枝末节的深究,则往往会一叶障目,只见树木,不见森林.教学中应当引导学生树立一种科学探究的态度和方法,在定性分析与定量计算两种方法之间达成一种动态的平衡.

2 定性分析的物理教学价值

2.1 定性分析有利于培养学生的核心素养

任何学科教学的核心价值之一是把前人从事智力活动的思想方法转化为学生认识能力.科学的思维方式决定一个人脑力劳动的水平和质量,是一个人认知素质的核心.很多时候,定性分析是一种高阶思维,某种意义上是一种智慧.充分挖掘教学内容中的定性分析内容,能使学生进入有高阶思维的深度学习,有利于培养学生学会用事实、逻辑进行推理和论证的思维能力,培养学生独特的、个性化的创新能力.

① 双缝干涉中条纹间距Δx与应该与实验本身的客观因素有关,与外界的人为因素无关.分析如图2所示杨氏实验装置,其中属于实验本身的客观因素有两方面:一是光本身的因素,即波长λ;二是实验装置的因素,有两条狭缝间的距离d,双缝与屏间的距离L,光源与单缝的距离l1,单缝与双缝的距离l2.

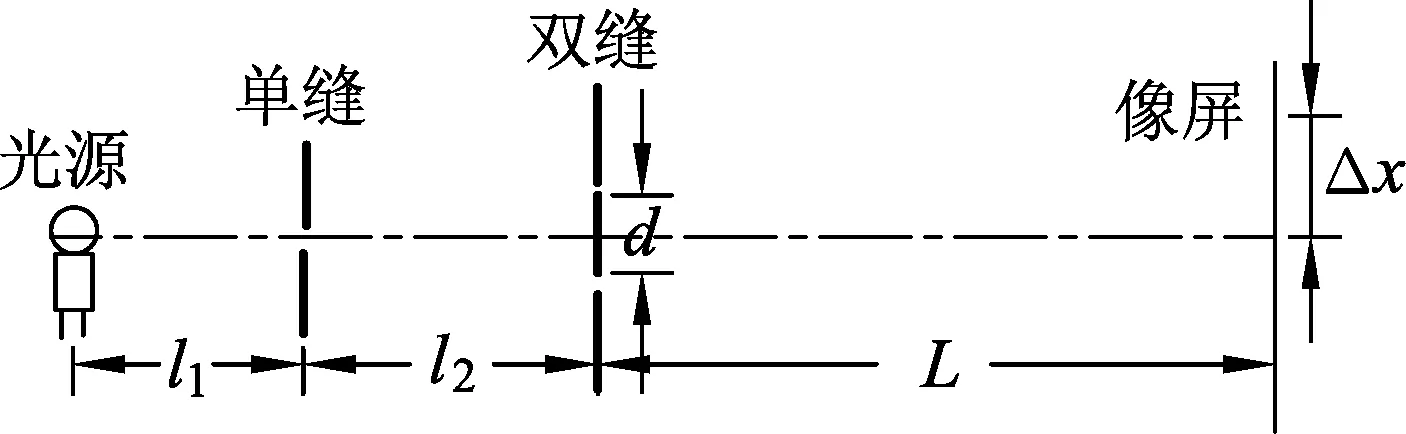
图2

② 考虑到干涉是从双缝开始的,光源与单缝只是为干涉创造了条件,不能决定之后如何干涉.故Δx与l1、l2无关.

③ 波长λ是反映光的波动性的量,波长λ越大,波动性越明显,则条纹宽度Δx亦越大,即λ与条纹宽度Δx是一种正相关的关系.

④ 再用极限思维:可以设想将d增大到足够时,将不再有明显干涉现象.不明显的干涉现象应该是各级条纹合在一起,即Δx→0.故狭缝间的距离d与条纹宽度Δx是一种负相关的关系.

诚然,上述分析过程在思维上并不完备,但其中用到正、负相关性分析,极限分析,量纲分析等思维方式无不是学生受用终生的,或者说是一种高品质的智慧.美国教育学家克罗韦尔指出“教育面临的最大挑战,不是技术,不是资源,不是责任感,而是……去发现新的思维方法”.教学中如能充分挖掘这些思维素质教育的素材,久而久之,必然能使学生的智慧产生质的飞跃.

2.2 定性分析有利于学生认清物理问题的本质

很多学生在处理物理问题时,不是首先根据题意进行定性分析,抓住问题的物理本质,而总是急于列出数学方程,无论何种问题都期望通过严格的数学推演去处理.一旦无法列出合理的数学方程或数学方程难以求解时,就往往束手无策,无以应对.

图3

教学中可以引导学生先作如下的定性分析:水平射程既取决于水平分速度,又跟空中飞行时间有关,抛出角α太大,则水平分速度小而空中飞行时间长,抛出角α太小,则水平分速度大而空中飞行时间短,都会影响水平射程.还可进一步分析,当α→0°和α→90°时,水平射程都为0,从而在脑中形成如图3的一幅图像:当α从0°逐渐增加到90°的过程中,水平射程将先变大再变小,当α取某个值时,水平射程将最大.这样的定性分析无疑对学生深刻理解抛体运动的整体特征大有裨益,而且也是培养学生动态思维的良好训练.

2.3 定性分析可以通过简单判断提高解题效率

物理中有很多问题并不需要计算出具体的数值,而是只需要进行一个比较或判断.这时如若一味的囿于定量分析,反而会使问题复杂化,甚至走入死胡同.

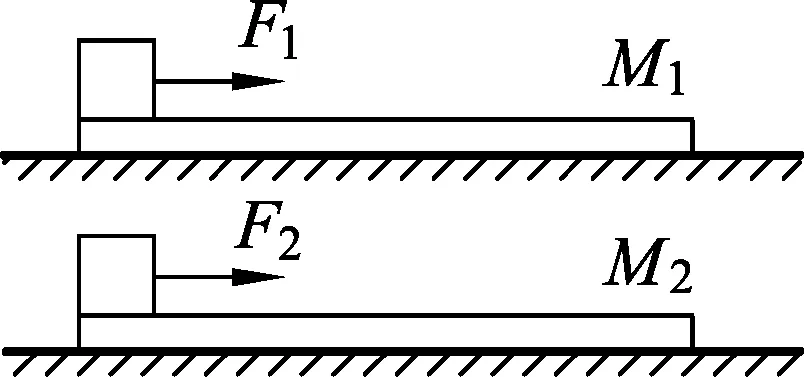
图4

例1.如图4所示,光滑水平面上放着两长度相同,质量分别为M1和M2的木板,在两木板的左端各放一完全相同的物块,开始时各物均静止.今在两物体上各作用一水平恒力F1、F2,当物块和木板分离时,两木板的速度分别为v1和v2,物体和木板间的动摩擦因数相同,则

(A) 若F1>F2,M1=M2,则v1>v2.

(B) 若F1v2.

(C) 若F1=F2,M1>M2,则v1>v2.

(D) 若F1=F2,M1v2.

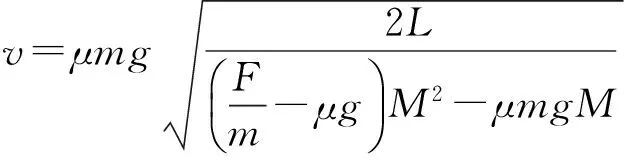
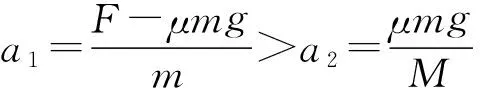
显然,求解过程比较麻烦,可谓是“高妙的数学,低劣的思维方法”.能不能运用定性分析得出结论呢?这其实是一个关于比较的方法论问题.通常,我们要比较不同事物的属性差异,总是建立在某种共性的基础上,否则比较就无从谈起.如本题中,对于选项(A)、(B),M相同则a2相同,F越大则a1越大,相应t越短,则v=a2t越小,(B)正确;对于选项(C)、(D),F相同则a1相同,M越大a2越小,相应t越短,则v=a2t越小,(D)正确.

我们从该例分析中不难发现,并非在所有的场合下繁复的定量计算都是必要的,有时定性分析的方法来得更为有效,而且其思维上更具有深刻性和灵活性.而定性思维则往往包含着丰富的辩证法思想,又要靠一定的物理直觉和洞察力,是对学生进行核心素养培养的重要途径.

2.4 定性分析能够为定量分析指明方向

很多学生经常反映物理题看不懂或不理解,也有一些学生一看到题目就急于列方程,求解过程思路混乱,经常遗漏一些环节,步骤散乱,做到哪里是哪里,最终无法顺利求解.其实,如果先对题目进行必要的定性分析,力求对问题的性质、解的概貌取得一个总体的估计和理解,理清思路、明确方向,就能最大程度避免以上问题,解题自然水到渠成.

例2.(2009年浙江高考题)某校物理兴趣小组决定举行遥控赛车比赛.比赛路径如图5所示,赛车从起点A出发,沿水平直线轨道运动L后,由B点进入半径为R的光滑竖直圆轨道,离开竖直圆轨道后继续在光滑平直轨道上运动到C点,并能越过壕沟.已知赛车质量m=0.1kg,通电后以额定功率P=1.5W工作,进入竖直轨道前受到阻力恒为0.3N,随后在运动中受到的阻力均可不计.图中L=10.00m,R=0.32m,h=1.25m,s=1.50m.问:要使赛车完成比赛,电动机至少工作多长时间?(取g=10m/s2)

图5

该题主要涉及圆周运动与平抛运动,按题意“要使赛车完成比赛”,既要确保赛车能通过圆轨道最高点,又要确保赛车能飞越壕沟.因此,只要依据恒定功率做功下的动能定理,先计算出赛车刚好能过圆轨道最高点情况下电动机需要的工作时间,再计算出赛车刚好能飞越壕沟情况下电动机需要的工作时间,取时间长者即可.经过这样的定性分析,既降低了题意理解上的难度,又理清了解题思路.

应该说,定性分析的教育价值远不止以上所述,但我们不难由此体会到定性分析与定量分析是辨证统一的,定性分析是定量分析的前提、保障,脱离了“质”的定量分析往往容易迷失方向,变成单纯的数学游戏;定量分析使定性分析更加科学、精确,脱离了“量”的定性分析往往不够深入.因此,在教学中,应引导学生定性分析与定量分析并重,有机结合,才能最大程度地培养和发展学生的核心素养.

1 赵凯华.定性与半定量物理学[M].北京： 高等教育出版社,1991：87-88.

2 沈金林.关于理性思辩的哲学思考与探究应用例析[J].物理教师，2005(1)：1-4.

3 宋艺华.例谈物理学中的定性分析与定量分析[J].物理教师，2009(5)：41-42.

2016-10-10)