基于混合效应的人工落叶松树冠轮廓模型*
高慧淋 董利虎 李凤日
(东北林业大学林学院 哈尔滨 150040)
基于混合效应的人工落叶松树冠轮廓模型*
高慧淋 董利虎 李凤日
(东北林业大学林学院 哈尔滨 150040)
【目的】以林木易测因子为预测变量,构建黑龙江省人工落叶松树冠最大外部轮廓及内部轮廓(未着叶部分)的预估模型,为进一步估计人工落叶松树冠表面积、树冠体积和树冠生物量提供依据。【方法】基于佳木斯市孟家岗林场49株解析木的枝解析数据,树冠外部轮廓模型采用分段回归技术,构建带有约束条件并满足生物学意义的连续性分段曲线模型,即在梢头处树冠半径为“0”,在整个树冠内外部轮廓的拐点的存在是唯一的,且在拐点处树冠半径达到最大值; 内部轮廓直接采用线性模型进行模拟。分析模型参数与林木变量之间的相关性,将关系密切的树木变量或变量组合引入到模型中并选出最优模型,以此作为基础模型分别建立单水平的外部轮廓及内部轮廓的混合效应模型,利用混合模型的固定效应部分对外部轮廓及内部轮廓进行模拟。【结果】以林木因子胸径、高径比、冠长及冠长率构建的分段抛物线模型能准确预估树冠的外部轮廓形状,利用胸径、高径比及冠长能有效预测树冠的内部轮廓形状。基于模型的拟合优度及检验指标,采用单水平(样地)混合模型能够显著提高模型的预测精度,外部轮廓混合效应预估模型的决定系数(R2)、均方误差根(RMSE)和平均偏差(Bias)分别为0.914 2、0.232 7 m和0.001 2 m,内部轮廓混合效应预估模型的R2、RMSE和Bias分别为0.723 5、0.147 0 m和-0.000 034 m。与基础模型相比,混合模型的R2都有所提高,RMSE、Bias都有所降低。在其他变量保持不变的条件下,外部轮廓半径分别随着胸径、冠长率的增大而增大,随着高径比、冠长的增大而减小; 内部轮廓半径均随着胸径、高径比及冠长的增大而增大。【结论】具有生物学意义的分段抛物线模型和线性模型分别能够有效描述人工落叶松树冠外部轮廓及内部轮廓的形状变化特征,加入混合效应后能够提高模型的拟合精度并改善组内的方差异性特征,基于混合效应模型中的固定效应部分,能够合理地对树冠外部轮廓及内部轮廓进行模拟,分段抛物线模型能够灵活地反映拐点在树冠内的移动规律线,简单的线性模型能够对内部轮廓进行准确预估。
人工长白落叶松; 外部轮廓; 内部轮廓; 非线性混合模型
作为树木的重要组成部分,树冠是树木生产力和生长活力的重要体现,是树木进行光合作用、呼吸作用和蒸腾作用等生理活动的主要场所,也是树木在林分中长势情况与周围环境相互作用及反馈调节的综合反映(Gilmore, 2001; 刘兆刚等, 2007)。树冠结构是树木构筑型研究的重要内容,可以用来描述树木之间的竞争、度量林木枯损模型中林木的生命力、预测树木树干生长以及构建树冠林火模型等(Fernandesetal., 2007; Russelletal., 2014)。树冠轮廓作为树冠结构的主要内容,是人们对一株树木最直观的总体印象,枝条作为树冠的重要组成部分,不仅是叶片的支撑体,而且其空间分布模式决定了树冠的轮廓(魏晓慧等, 2012)。树冠的轮廓和大小与树木生产力密切相关,进而影响树木的生长和枯损(Jacketal., 1992; Soaresetal., 2001; Crecente-Campoetal., 2009)。因此,对树冠轮廓进行研究具有重要意义。
对于树冠轮廓模型的研究,最初的做法是将树冠沿着垂直树干轴心的方向进行划分,将不同的部分看成不同的几何形体(圆形、椭圆形等),进而达到描述树冠轮廓的目的(Hann, 1999),也有学者利用分形维数建立了预估树冠形状的模型(Zeideetal., 1991; 刘兆刚等, 2005),但以上研究存在的问题是几何形体在实际应用中不灵活。为了探究更加灵活的描述树冠轮廓的模型形式,很多学者构建枝条属性因子(基径、枝长、着枝角等)预估模型,利用三角函数关系计算树冠半径,以达到间接描述树冠外侧轮廓的目的(Roehetal., 1997; Li, 2004);还有学者利用树木变量如胸径、树高及冠长率等预估树干表面积、树冠体积及树冠形状指数,间接地描述树冠形状(刘兆刚等, 1996)。这些研究相对于利用几何形体来描述冠形非常灵活,但仍不能够直观展现出树冠的轮廓特性。Marshall 等(2003)将树冠在最大冠幅处划分为2部分,用2个不同的模型分别建立了预测上部和下部树冠任意位置处树冠轮廓,Crecente-Campoa等(2009; 2013)、卢军(2008)也做过类似的研究。这些研究在描述冠形上具有非常好的灵活性和直观性,但存在的问题是分别独立拟合2个部分的冠形曲线不能保证在断点的连续性。为克服这一缺点,Baldwin等(1997)、Davies等(2008)以胸径及冠长率等为自变量直接建立了树冠外部轮廓的连续型曲线,郭艳荣等(2015)、Dong等(2015)总结了已经发表的描述树冠轮廓的模型,并对其进行了比较。高慧淋等(2015)基于样条函数理论,推导出满足冠形曲线生物学约束的连续分段抛物线函数,构建了人工红松(Pinuskoraiensis)的平均轮廓模型,但并未解决最大轮廓模拟的问题。此外,除Baldwin等(1997)直接建立了预测火炬松(Pinustaeda)树冠未着叶部分(“真空”)的轮廓模型外,在国内尚未发现对树冠内部轮廓模型进行研究的报道。
鉴于此,本研究基于单水平非线性混合效应模型,以树木易测因子为预测变量,利用分段抛物线函数理论构建含有约束条件的长白落叶松(Larixolgensis)树冠最大外部轮廓预估模型,利用线性模型构建内部轮廓预估模型,分析最大外部轮廓的拐点与树木变量之间的关系,为进一步估计人工落叶松树冠体积、树冠表面积及树冠生物量提供依据。
1 研究区概况及研究方法
1.1 研究区概况
研究区位于黑龙江省佳木斯市孟家岗林场(130°32′—130°52′E,46°20′—46°30′N)。该地区地形以低山丘陵为主,平均坡度15°,平均海拔250 m。气候类型为东亚大陆性季风气候,冬季寒冷干燥,夏季温暖潮湿,年平均气温2.7 ℃。年平均降水量550 mm,全年日照1 955 h,无霜期120天左右。土壤类型以暗棕壤为主,而暗棕壤中又以典型暗棕壤分布最为广泛。该林场森林覆盖率达80%以上,其中人工林约占67%。
1.2 研究方法
1.2.1 数据来源 2015年8—9月,在不同林龄、不同密度的长白落叶松人工林中设置面积为0.04 hm2或0.06 hm2的标准地7块。对标准地内所有树木进行每木检尺,测量树木的胸径(DBH,cm)、树高(tree height,HT,m)及冠幅(crown width,CW,m),采用等断面积径级标准木法将标准地内全部树木划分为5级,每级选取1株标准木,此外每块标准地分别再选取1株优势木和1株劣势木,共获取49株标准木。
所有解析样木在伐倒前均实测DBH和CW,在树干标注北向,为伐倒后确定枝条的方位角提供标准。解析木伐倒后实测HT,将树冠下部至少含有1个活枝的枝条基径位置作为树冠基部。实测树冠基部至树梢的距离,定义为树冠长度(crown length,CL,m),CL与HT的比值作为冠长率(crown rate,CR),HT与DBH的比值为高径比(height to diameter ratio,HD)。将整个活冠由树冠基部到树梢的方向按照1 m区分段进行划分,不足1 m的部分定义为梢头。从梢头开始对所有活轮枝进行解析,每一轮所有枝条以北向为准按照顺时针方向编号,测量所有轮生枝的方位角(azimuth angle,AZ,°)、着枝角(branching angle,VA,°)、基径(branch diameter,BD,mm)、枝长(branch length,BL,cm)、弦长(branch chord length,BC,cm)、着枝深度(depth into the crown,DINC,cm)及未着叶部分的弦长等枝条属性因子。每一轮分别选取一个最大的枝条和未着叶长度最小的枝条作为构建人工落叶松外部轮廓和内部轮廓模型的样本,本研究共选取509个最大枝条和501个未着叶长度最小的枝条。利用选取的最大枝条及未着叶长度最小的枝条的弦长与着枝角的三角函数关系分别计算相应位置处的外部轮廓半径(outer crown radius,OR,m)和内部轮廓半径(inner crown radius,IR,m),每个枝条的DINC与CL的比值定义为相对冠深(relative depth into the crown,RDINC)。将所有解析样木按照近似3∶1的比例随机分为建模样本和独立检验样本,分别用于树冠最大外部轮廓和内部轮廓模型的拟合及独立性检验。本研究所用解析样木变量和枝条变量统计详见表1。
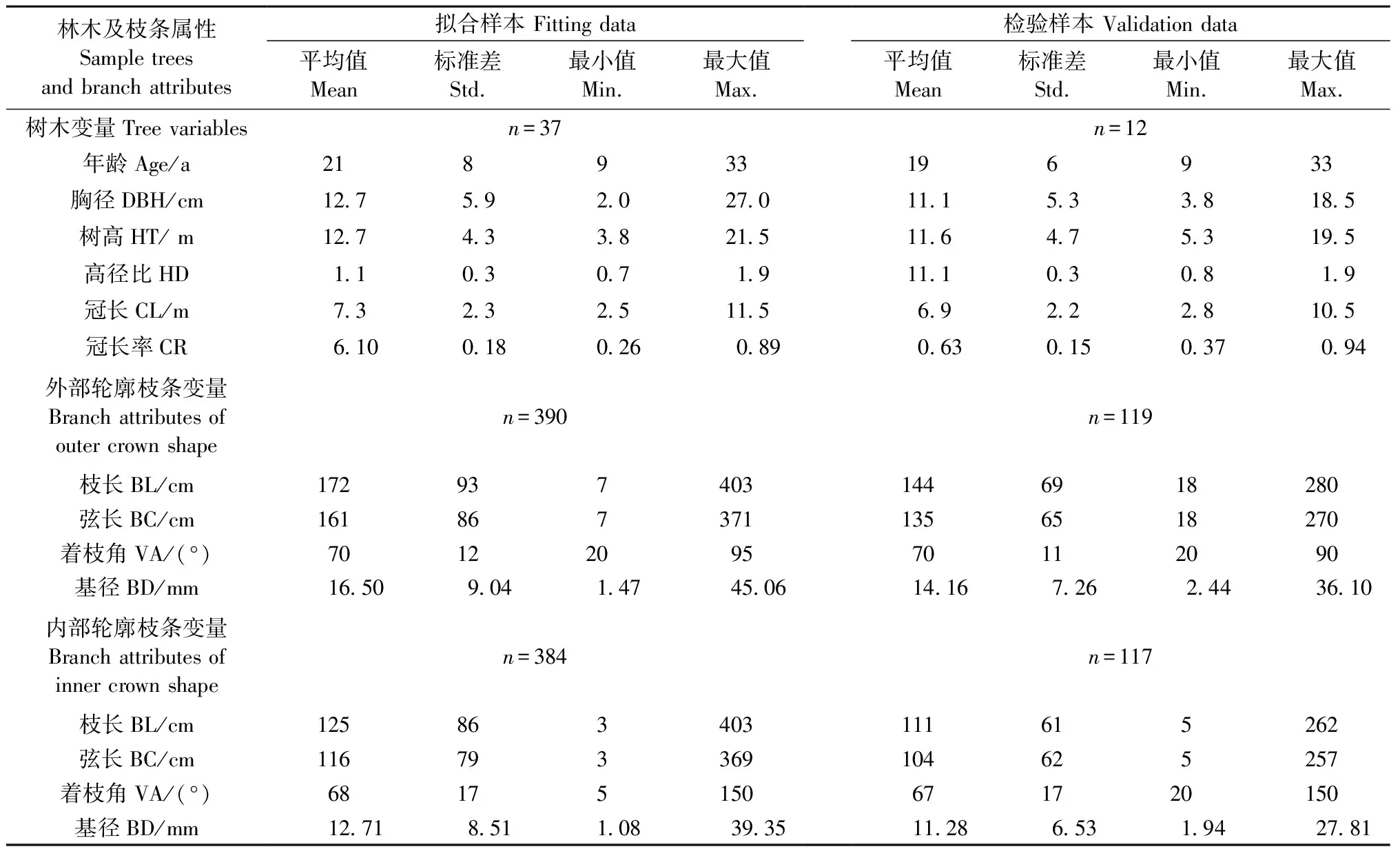
表 1 人工落叶松解析木及枝条变量统计
1.2.2 基础模型的选取 树冠外部轮廓模型的研究已有很多成果,已经从简单的几何形体过渡到了非常灵活的模型形式(Hatchetal., 1975),其中变指数方程模型形式简单且直观(Rautiainenetal., 2005)。Max等(1976)成功将分段函数应用到了描述树干形状的研究中;高慧淋等(2015)研究表明,分段抛物线模型具有很好的灵活性,能够比较精确地预测树冠轮廓的拐点位置,且模型形式简单,便于应用。因此,本研究基于分段抛物线函数构建含有约束条件的人工落叶松树冠外部轮廓模型,形式如下:
OR=b1·RDINC+b2·RDINC2+
(1)
式中: OR为树冠外部轮廓半径; RDINC为相对冠深;b1,b2,b3,a1为模型参数,a1为2段抛物线的连接点。
模型(1)具有如下性质: 1) 满足在梢头位置树冠半径为“0”的生物学特性; 2) 树冠轮廓模型存在拐点,且拐点是唯一的; 3) 模型在连接点处连续,即RDINC=a1时,导数连续。
对于树冠内部轮廓模型,通过对数据进行初步分析,树冠内部未着叶部分的半径与RDINC基本为线性关系。因此,本研究采用与Baldwin等(1997)相同的方法构建人工落叶松树冠内部轮廓模型,形式如下:
IR=c1+c2·RDINC。
(2)
式中: IR为树冠内部轮廓任意位置处的树冠半径;c1,c2为模型参数; 其他变量定义同上。

(3)
1.2.3 非线性混合效应模型 本研究采用单水平非线性混合效应模型构建人工落叶松树冠外部轮廓及内部轮廓模型,单水平非线性混合效应模型的形式如下:
式中:i,j分别代表第一水平和观测值,本研究仅考虑样地效应,因此yij为第i个样地中第j(枝条)次观测值;M为区分组的数量(样地数);ni为每一个区分组内的观测值个数;β为(p×1)维固定效应向量;bi为(q×1)维随机效应向量;Aij,Bij为设计矩阵;D为随机效应的方差-协方差矩阵;Ri为区分组内的方差-协方差矩阵;σ2为方差;eij为模型的误差项;Gi为描述方差异质性的对角矩阵;Γi为样地内误差的相关性结构。
混合模型中的关键步骤就是确定参数效应。本研究将所有可能的参数或参数组合都作为随机效应进行拟合,利用AIC、BIC和对数似然值统计指标对模型进行评价,AIC、BIC越小,对数似然值越大,模型的拟合效果越好。为了避免过多参数化问题,分别选取含有不同个数参数效应的最优模型进行似然比检验(LRT),选取参数较少而模型较显著的模型作为最优模型。
(5)
(6)
模型的拟合和检验除采用AIC、BIC、Log-likelihood 3个统计指标外,还采用平均误差(Bias)、均方根误差(RMSE)和确定系数(R2)3个指标,公式如下:
(7)
(8)
(9)
模型的独立性检验采用独立检验样本数据对最终确定的模型进行综合评价。混合模型固定效应的检验与传统的检验方法相同,而其关键就是对随机参数的预测,随机参数的计算公式如下:
(10)

2 结果与分析
2.1 基础模型
依据各参数与树木变量之间的相关性检验,将与各参数相关性较强的树木变量或变量组合引入到模型中。为充分减小变量之间的共线性并保证模型精度要求,对于树冠最大外部轮廓预估模型,最终引入到模型中的树木变量为DBH,CR,CL和HD。因此,人工落叶松树冠外部轮廓预估模型的具体形式如式(11)所示,内部轮廓模型的具体形式如式(12)所示:
(11)

(1)探索出的新工艺为黄观音鲜叶→轻晒青(地表温度28 ℃,空气湿度64%,30 min)→轻摇青(2次,每次1 min)→室内萎凋(空调控温)→揉捻(40~60 min)→发酵(4~5 h,控温控湿)→理条(针型)→烘干→提香→成品茶,制成的黄观音红茶花香明显,滋味醇和甘甜,酚氨比较低,综合评价比传统工艺更为理想。
RDINC。
(12)
式中:bij,aij,cij均为模型参数;其他符号定义同上。
2.2 混合效应参数的确定
本研究采用以往研究方法,将所有参数及其组合形式均作为随机效应进行拟合。由于模型(11)参数较多,当随机参数达到5个以上时,模型AIC、BIC明显增大,而Log-likelihood则明显降低,且不易收敛。因此,对于树冠外部轮廓模型,本研究选定随机参数最多为5个,对于含有不同数量随机效应的模型,分别选取1个最优的模型进行似然比检验,结果详见表2。对于内部轮廓,将所有参数及其组合形式都作为随机效应进行拟合,对于含有不同数量随机效应的最优模型,进行似然比检验,选出最优模型形式,结果详见表2。

表2 基于样地效应的混合模型拟合结果
由表2可知,外部轮廓模型中不同随机效应参数组合的拟合结果显示,混合模型的AIC、BIC相对于基本模型(11)都大幅度降低,Log-likelihood都大幅度提高,这说明混合模型的拟合效果明显优于基本模型。对于模型(11.1)-(11.4),随着随机参数效应的增加,模型的拟合效果都明显提高,最终选择含有4个随机参数效应的模型(11.4)为最优模型,且与模型(11.3)的似然比检验显著。由于似然比检验仅对于嵌套式模型有效,而对于非嵌套模型会有一定的问题,因此,模型(11.3)与(11.2)之间没有进行似然比检验,但模型(11.3)与(11.2)相比,AIC及BIC都明显降低,Log-likelihood都明显提高,因此模型(11.3)仍优于(11.2)。对于树冠的内部轮廓模型,混合模型的AIC、BIC相对于基本模型(12)均有一定程度降低,而Log-likelihood有一定幅度提高,这说明内部轮廓模型的混合模型优于基本模型。对含有不同随机效应的混合模型进行比较和似然比检验,结果含有2个随机效应参数的混合模型(12.2)拟合效果最好。因此,外部轮廓模型和内部轮廓模型分别选择模型(11.4)和模型(12.2)为最优模型。
2.3 方差-协方差矩阵的确定
混合模型中很重要的部分就是确定组间的方差-协方差矩阵。对模型(11.4)和(12.2),本研究对比了对角矩阵和广义正定矩阵对混合模型拟合效果的影响,结果见表3。

表3 基于随机参数效应不同方差协方差结构混合模型拟合结果比较
由表3可知,无论对于外部轮廓模型还是内部轮廓模型,广义正定矩阵都表现出了很好的拟合效果,且由似然比检验结果可知,广义正定矩阵与对角矩阵之间的差异性显著(P< 0.05)。因此,本研究对于模型(11)和(12)均采用广义正定矩阵作为随机效应的方差-协方差矩阵假设形式。
2.4 模型参数估计及独立性检验
为了解释组内方差的异质性,本研究采用幂函数和指数函数来消除异方差,2种方差模型对于模型的拟合效果见表4。

表4 基于不同方差函数混合效应模型拟合效果比较
由表4可知,对于模型(11.4.1)和(12.2.1),采用指数函数都明显提高了模型拟合精度。对于基础模型(11)和(12),模型的残差呈现明显的喇叭状,且波动范围较广(图1a、图1c)。通过混合效应模型并采用指数函数进行拟合后,模型(11)的残差得到了明显改善,残差分布范围明显变小(图1b、图1d),而模型(12)的残差改善效果较模型(11)稍差一些,但残差的分布范围也明显变小。混合模型(11.4.1.2)和(12.2.1.2)及基础模型(11)和(12)的参数估计结果详见表5、表6。对于基础模型(11)和(12),绝大多数参数估计效果都比较好,而通过混合模型拟合后,所有固定参数的拟合效果都明显提高。基础模型(11)的Bias、RMSE及R2分别为-0.004 5,0.288 1,0.868 5,而混合模型的Bias、RMSE及R2分别为0.001 2,0.232 7,0.914 2,可见混合模型的拟合效果较好(表5)。基础模型(12)的 Bias、RMSE及R2分别为-0.000 033,0.158 5,0.678 6,混合模型的Bias、RMSE及R2分别为-0.000 034,0.147 0,0.723 5,混合模型拟合效果优于基础模型(表6)。利用独立检验样本对外部轮廓的基本模型和混合模型进行检验,混合模型的拟合效果优于基本模型; 对于内部轮廓,混合模型的拟合效果明显优于基本模型(表7)。由图2中3株不同林木树冠外部和内部轮廓的实际形状与模拟结果可知,分段抛物线和线性模型能够对人工落叶松树冠外部及内部轮廓进行很好地模拟。

图1 外部轮廓及内部轮廓预估模型残差Fig.1 Residual plots for outer and inner crown shape predicted modelsa,b分别基于基础模型(11)和混合模型(11.4.1.2); c,d分别基于基础模型(12)和混合模型(12.2.1.2)。a,b were residual plots for basic model(11)and mixed effect model(11.4.1.2); c,d were residual plots for basic model(12)and mixed effect model(12.2.1.2).

模型Modelsa11a12b11b12b21b22b31b32BiasRMSER2(11)估计值Estimate0 6603-0 03052 80430 1532-4 47582 76689 7491-1 3788标准误Standarderror0 10140 01260 19200 00730 29910 26165 13020 6805-0 00450 28810 8685(11 4 1 2)估计值Estimate0 7095-0 12972 17760 1726-4 35593 52228 6742-1 5422标准误Standarderror0 06130 07470 26780 01350 22360 31731 35080 19180 00120 23270 9142方差协方差Variance⁃covariancestructureσ2=0.0040,σ2a12=0.0220,σ2b11=0.3788,σ2b12=0.0010,σ2b32=0.0269,σa12b11=0.9530σa12b12=-0.8530,σa12b32=-0.9240,σb11b12=-0.9710,σb11b32=-0.7640,σb12b32=0.5880

表6 内部轮廓基本模型与混合模型参数估计结果

表7 基本模型与混合模型的检验结果

图2 不同林木树冠实际形状与模拟形状对照Fig.2 Comparison between the actual crown shape and simulation shape for different trees

图3 不同大小树木树冠外部轮廓及内部轮廓模拟Fig.3 Simulation for outer and inner crown shape of different tree sizes
2.5 树冠冠形模拟
基于混合模型的固定效应,分别模拟了不同大小的人工落叶松树冠外部轮廓和内部轮廓(图3)。外部轮廓预估模型中包含的树木变量为4个,模拟方法是固定其中的3个变量从而模拟树冠半径与剩余变量的变化关系,所固定的树木变量值均接近平均值。由图3a可知,在树木HD,CL,CR保持不变时,树冠外部轮廓半径随着DBH增加而呈现明显的增加趋势,且变化幅度较大。DBH为8,12,16 cm的外部轮廓的拐点分别为0.677,0.756,0.835,这说明在其他变量保持不变的情况下,外部轮廓的拐点有明显的向树冠基部移动的趋势,而随着DBH的增大,内部轮廓也逐渐偏离树干而逐渐增大。对比可知,HD对树冠外部轮廓和内部轮廓的影响较小,且主要影响靠近树冠基部部分的形状(图3b)。在DBH,CL,CR保持不变时,外部轮廓和内部轮廓的半径均随着HD增大而呈现减小的趋势。HD为0.8,1.0,1.2的外部轮廓的拐点位置分别为0.781,0.769,0.756,即随着HD的增大,外部轮廓的拐点有向树梢移动的趋势,内部轮廓的半径随着HD的增大而逐渐增大。由于在外部轮廓模型中,CL与2段分段抛物线的连接点的位置关系密切,因此,该变量主要影响外部轮廓中连接点以下的形状(图3c)。在其他变量保持不变时,外部轮廓半径随着CL的增加而减小,且当CL为7.5,8.5,9.5时,拐点分别为0.726,0.686,0.661,即逐渐向树梢方向移动,而内部轮廓半径则随着CL的增加而增加。由图3d可知,树冠外部轮廓半径随着CR的增大而逐渐增大,趋势明显。当CR分别为0.4,0.6,0.8时,树冠外部轮廓的拐点位置分别为0.651,0.765,0.902,拐点逐渐向树冠基部移动。由于树冠内部轮廓模型与CR没有密切的关系,因此,图中内部轮廓曲线为当DBH=12 cm、HD=1.2、CL=7.0 m时平均状态的内部轮廓。
3 讨论
3.1 树冠轮廓预估模型的构建
分段多项式将若干子模型连接成一个单一模型,这种模型形式不仅具有简洁性,而且具有非常大的灵活性,因此在林业上得到了广泛应用(Maxetal., 1976)。Martin等(1984)研究表明,精确地构建经验模型的预估精度要优于理论模型,而Vanclay(1994)则认为从模型应用的角度考虑,理论模型要优于经验模型,原因是理论模型对建模样本范围外的数据的预测效果要优于经验模型。因此,模型的生物学意义越来越受到重视。
以往对于树冠轮廓的研究,大多数学者均采用将树冠在最大半径处分成2个独立的部分(“阳冠”和“阴冠”)分别建模的方法(Marshalletal., 2003; Crecente-Campoetal., 2009; 2013),这种方法对于“阳冠”的拟合效果一般较好,R2可达到0.90以上(Honer, 1971; Crecente-Campoetal., 2009),但对于“阴冠”的拟合效果稍差一些。本研究采用具有生物学意义的分段抛物线模型直接拟合整个树冠的外部轮廓,在未考虑混合效应的情况下,R2已经达到0.85以上(表5),而国内相关研究采用简单抛物线等模型形式,R2仅达到了0.80左右(郭艳荣等, 2015)。这充分说明,采用具有生物学意义的分段抛物线模型能够提高模型的预估精度。为了解释样地之间的变异性,本研究采用了单水平的混合效应模型。由混合模型与基本模型之间的拟合及检验结果对比可知,混合效应模型充分解释了样地内的变异,提高了模型的预估能力。从残差图效果来看,混合模型采用指数函数能够使得AIC、BIC显著降低,Log-likelihood增大,模型的残差分布范围变小,残差图得到了一定程度的改善。
人工落叶松树冠内部其针叶的着生出现“真空”现象,形成的原因是靠近枝条基部由于光照不足有一段距离无叶片分布。因此,为能够准确估计人工落叶松着叶部分的树冠体积提供依据,本研究建立了内部未着叶部分的轮廓模型。通过对数据进行初步分析,内部轮廓的半径与RDINC基本呈线性关系,与Baldwin等(1997)对火炬松内部轮廓的研究结果一致。采用混合模型后,模拟的R2达到了0.70以上,这说明采用简单的线性模型能够很好地模拟人工落叶松内部未着叶部分的轮廓模型。本研究仅采用了单水平的非线性混合效应模型,关于多水平的混合效应模型能否提高模型的拟合精度会在今后的研究中继续探讨。
3.2 树冠轮廓与树木变量的关系
国内外树冠轮廓预估模型中引入树木变量因树种的差异而不同,而普遍采用的树木变量包括DBH,HD,CR等(刘兆刚等, 1996; Daviesetal., 2008; 郭艳荣等, 2015)。本研究采用再参数化方法,对于外部轮廓模型最终选择了DBH,HD,CL及CR作为解释变量,内部轮廓模型最终选择了DBH,HD及CL作为自变量,这与国内外大多数研究结果是一致的。对于密度是否应该作为变量引入到模型中,很多学者的观点并不相同(Larocqueetal., 1994; Hann, 1999),但总体上,随着密度的改变,树冠冠形的变化可能会相对滞后,引入密度指标可能会得到不合理的预估模型(Larocqueetal., 1994)。因此,本研究没有直接引入密度指标,而是引入了能间接反映林分密度的变量HD。
为探究树冠最大轮廓拐点与树木变量的关系,本研究基于混合模型中的固定参数模拟了树冠外部轮廓拐点与树木变量之间的关系。对于人工落叶松,DBH、CL及CR都对树冠外部轮廓具有显著的影响作用,HD对外部轮廓的影响相对较小,但混合模型中对该变量参数的估计是显著的。此外,HD是与分段抛物线的连接点有关的,主要影响连接点以下的冠形。DBH对外部轮廓形状及拐点位置的影响比较显著,与实际情况符合。在加入树高的影响后,CR对树冠外部轮廓的影响与CL是不同的。因此,本研究采用了既能反映树冠尖削度的指标(HD),还采用了能反映树冠相对长度的指标(CR),能够充分真实地反映树冠的外部轮廓。
树冠的内部轮廓对于树木变量变化的反映相对外部轮廓较弱,仅DBH对其影响较显著。Baldwin等(1997)研究表明,火炬松树冠内部轮廓是由低于树梢的某一位置延伸到树冠基部的一条直线,本研究得出了相同的结论:在其他树木变量保持不变的情况下,随着DBH的增大,树冠内部轮廓的直线逐渐向树冠基部的方向移动,随着HD的增大,逐渐向树梢方向移动,随着CL的增大,逐渐向树梢方向移动。
4 结论
本研究采用分段抛物线函数理论,构建了人工落叶松树冠最大外部轮廓及内部轮廓的非线性混合效应模型,基于R软件对模型参数进行求解,得出如下结论: 分段抛物线模型能够真实准确地反映树冠外部轮廓的形状和拐点在树冠内的变化规律,线性模型能够准确地描述内部轮廓的形状。外部轮廓和内部轮廓模型加入混合效应后能够明显提高模型的拟合精度,对组内的异方差性也有所改善。人工落叶松树冠的外部轮廓和内部轮廓形状分别与胸径、高径比、树冠长度及冠长率和胸径、高径比及树冠长度有密切关系。
高慧淋,李凤日,董利虎. 2015. 基于分段回归的人工红松冠形预估模型. 北京林业大学学报, 37(3): 76-83.
(Gao H L, Li F R, Dong L H. 2015. Crown-shape model of aPinuskoraiensisplantation in northeastern China. Journal of Beijing Forestry University, 37(3): 76-83. [in Chinese])
郭艳荣,吴保国,郑小贤,等. 2015. 杉木不同龄组树冠形态模拟模型研究.北京林业大学学报, 37(2): 40-47.
(Guo Y R, Wu B G, Zheng X X,etal. 2015. Simulation model of crown profile for Chinese fir (Cunninghamialanceolata) in different age groups. Journal of Beijing Forestry University, 37(2): 40-47. [in Chinese])
刘兆刚,郭承亮,袁志强. 1996. 落叶松人工林树冠形状的预估. 东北林业大学学报, 24(6): 15-21.
(Liu Z G, Guo C L, Yuan Z Q. 1996. Estimation of crown form forLarixolgensisplantation. Journal of Northeast Forestry University, 24(6): 15-21. [in Chinese])
刘兆刚, 刘继明, 李凤日, 等. 2005. 樟子松人工林树冠结构的分形分析. 植物研究, 25(4): 465-470.
(Liu Z G, Liu J M, Li F R,etal. 2005. Fractal analysis of crown structure inPinussylvestrismongolicaplantation. Bulletin of Botanical Research, 25(4): 465-470. [in Chinese])
刘兆刚,李凤日. 2007. 樟子松人工林树冠内一级枝条空间的分布规律. 林业科学, 43(10): 19-27.
(Liu Z G, Li F R. 2007. Modeling of spatial distribution of primary branches within the crowns ofPinussylvestrisstands. Scientia Silvae Sinicae, 43(10): 19-27. [in Chinese])
卢 军. 2008.帽儿山天然次生林树冠结构和空间优化经营.哈尔滨: 东北林业大学博士学位论文.
(Lu J. 2008.Crown structure and optimal spatial management for secondary forest in Maoershan Mountain. Harbin: PhD thesis of Northeast Forestry University. [in Chinese])
魏晓慧,孙玉军,黄冬辉. 2012. 马尾松人工林树冠结构研究. 西北农林科技大学学报:自然科学版, 40(11): 125-130,138.
(Wei X H, Sun Y J, Huang D H. Study on crown structure for Masson pine plantation. Journal of Northwest A&F University:Natural Science Edition, 40(11): 125-130,138. [in Chinese])
Baldwin V C, Peterson K D. 1997. Predicting the crown shape of loblolly pine trees. Canadian Journal of Forest Research, 27(1): 102-107.
Crecente-Campo F, Marshall P, Lemay V,etal. 2009. A crown profile model forPinusradiataD. Don in northeastern Spain. Forest Ecology and Management, 257(12): 2370-2379.Crecente-Campo F,lvarez-González J G, Castedo-Dorado F,etal. 2013. Development of crown profile models forPinuspinasterAit.andPinussylvestrisL. in northwestern Spain. Forestry, 86(4): 481-491.Davies O, Pommerening A. 2008. The contribution of structural indices to the modelling of Sitka spruce (Piceasitchensis) and birch (Betulaspp.) crowns. Forest Ecology and Management, 256(1): 68-77.
Dong C, Wu B G, Wang C D,etal. 2016. Study on crown profile models for Chinese fir (Cunninghamialanceolata) in Fujian Province and its visualization simulation. Scandinavian Journal of Forest Research, 31(3): 302-313.
Fernandes P M, Rigolot E. 2007. The fire ecology and management of maritime pine (PinuspinasterAit.). Forest Ecology and Management, 241(1/3): 1-13.Gilmore D W. 2001. Equations to describe crown allometry ofLarixrequire local validation. Forest Ecology and Management, 148(1/3): 109-116.
Hann D W. 1999. An adjustable predictor of crown profile for stand-grown Douglas-fir trees. Forest Science, 45(2): 217-225.
Hatch C R, Gerrard D J, Tappeiner J C. 1975. Exposed crown surface area: a mathematical index of individual tree growth potential. Canadian Journal of Forest Research, 5(5): 224-228.
Honer T G. 1971. Crown shape in open- and forest-grown Balsam Fir and Black Spruce. Canadian Journal of Forest Research, 1(4): 203-207.Jack S B, Long J N. 1992. Forest production and the organization of foliage within crowns and canopies. Forest Ecology and Management, 49(3/4): 233-245.Larocque G R, Marshall P L. 1994. Crown development in red pine stands. I. Absolute and relative growth measures. Canadian Journal of Forest Research, 24(4): 762-774.
Li F R. 2004. Modeling crown profile ofLarixolgensistrees. Scientia Silvae Sinicae, 40(5): 16-24.
Marshall D D, Johnson G P, Hann D W. 2003. Crown profile equations for stand-grown western hemlock trees in northwestern Oregon. Canadian Journal of Forest Research, 33(11): 2059-2066.
Martin G L, Ek A R. 1984. A comparison of competition measures and growth models for predicting plantation red pine diameter and height growth. Forest Science, 30(3): 731-743.
Max T A, Burkhart H E. 1976. Segmented polynomial regression applied to taper equations. Forest Science, 22(3): 283-289.
Rautiainen M, Stenberg P. 2005. Simplified tree crown model using standard forest mensuration data for Scots pine. Agricultural and Forest Meteorology, 128(1): 123-129.
Roeh R L, Maguire D A. 1997. Crown profile models based on branch attributes in coastal Douglas-fir. Forest Ecology and Management, 96(1/2): 77-100.
Russell M B, Weiskittel A R, Kershaw J A. 2014. Comparing strategies for modeling individual-tree height and height-to-crown base increment in mixed-species Acadian forests of northeastern North America. European Journal of Forest Research, 133(6): 1121-1135.
Soares P, Tomé M. 2001. A tree crown ratio prediction equation for eucalypt plantations. Annals of Forest Science, 58(2): 193-202.
Vanclay J K.1994. Modelling forest growth and yield: application to mixed tropical forests. CAB International, Wallingford.
Zeide B, Pfeifer P. 1991. A method for estimation of fractal dimension of tree crown. Forest Science, 37(5): 1253-1265.
(责任编辑 石红青)
Crown Shape Model forLarixolgensisPlantation Based on Mixed Effect
Gao Huilin Dong Lihu Li Fengri
(SchoolofForestry,NortheastForestryUniversityHarbin150040)
【Objective】 The maximum outer and inner (defoliation part) crown shape predicted models forLarixolgensisplantation were developed based on the easily measurable individual tree variables to provide suitable approach to estimate crown surface area, crown volume and crown biomass forL.olgensisplantation. 【Method】Using branch analysis data of 49 trees from Mengjiagang forest farm in Heilongjiang Province, the models of maximum outer crown and inner shape were developed. Outer crown shape predicted model constructed the continuous segmented equation with constraints and biological reasoning by employing the segmented regression technology. The outer crown radius equaled “0” at the tree tip and the inflection point where crown radius got maximum value was unique. Different from outer model, the straight line was used to model the inner crown shape. The relationships between the estimated parameters and tree variables were analyzed and the most intimate variable or variables combination were included in the models. The best models were selected as the basic model to develop the one level mixed effect model for the outer and inner crown shape. Based on the fixed effect of models, the outer and inner crown shapes were simulated. 【Result】 Diameter at breast height (DBH), tree height to diameter ratio (HD), crown length (CL) combined with crown ratio (CR) would predict the outer crown shape with the high accuracy. While the inner crown shape was modeled as DBH, HD and CL. The predicted accuracy was significantly increased by using 1 level (plot) mixed effect models compared with the basic models based on the goodness-of-fit and validation criteria. The coefficients of determination (R2), RMSE and average bias (Bias) of outer crown shape predicted model were 0.914 2,0.232 7 m,0.001 2 m respectively and 0.723 5,0.147 0 m,-0.000 034 m for the inner crown shape predicted model,respectively. Compared to the basic model,R2increased,while RMSE and Bias decreased for the mixed effect model. The segmented polynomial can reflect the variation regularity of the inflection point within the entire crown. The radii of the outer crown shape increased with the increase of DBH and CL, and decreased with HD and CL while other variables kept constant. The radii of inner crown shape increased with DBH, HD and CL.【Conclusion】 The segmented polynomial equation with biological reasoning and linear model could effectively reflect the outer and inner crown shape. The models which possessed the random effect have improved the prediction accuracy and heteroscedasticity features of the models. Based on the fixed effect, the model could give reasonable simulation to the outer and inner crown shape. The segmented polynomial equation was flexible to describe the movement regularity of inflection points within the entire crown. Singular linear model performed well in modeling inner crown shape.
larch (Larixolgensis) plantation; outer crown shape; inner crown shape; nonlinear mixed effect model
10.11707/j.1001-7488.20170310
2016-03-21;
2016-04-19。
国家自然科学基金项目(31570626); 中央高校基本科研业务费专项资金资助(2572015AA23)。
S757
A
1001-7488(2017)03-0084-10
*李凤日为通讯作者。

