圆锯片的压痕应变法残余应力测试与分析*

王韵璐 曹 瑜 李敏敏 王 正

圆锯片广泛用于木材、石材、金属、混凝土等多种材料的切割[1]。圆锯片构件在机加工、热处理、焊接、整平和适张作业加工过程中都会产生不同程度的残余应力，这些残余应力的存在会严重影响锯片的正常使用。圆锯片构件中的残余应力是指在没有对其施加外力时，圆锯片内部存在保持自相平衡的应力系统，亦是圆锯片构件的弹性和塑性各向异性的反映。圆锯片中的残余应力是固有应力或内应力的一种，对结构可靠性有很大作用[2]，特别是对其结构强度、疲劳寿命、尺寸稳定性和脆性断裂的影响较大。因此，做好降低或消除圆锯片构件的残余应力工作尤为重要。

圆锯片等金属构件的残余应力可通过测量进行很好的定量研究，常用方法为压痕应变法、X射线衍射法、盲孔法[3]和激光全息小孔法。其中，盲孔法和激光全息小孔法原理及其测量仪器均很成熟，适宜实验室应用；X射线衍射法[4,5]和压痕法更偏向于工程实际应用。如张占宽、习宝田等人用国产X-350A型X射线应力测试仪对圆锯片初始应力和多点加压适张后的残余应力进行了测量，确定了其残余应力分布规律[1,6,7]。压痕应变法是利用测量球形压头产生的压痕外弹性区的应变变化来计算残余应力的方法。当球形压头压入圆锯片测点时，测点上的应变花产生应变变形增量，即可获知压头压入测点后压痕周围弹性区的应变增量，就能得到构件表面的原始残余应力[8]。压痕应变法作为一种新型残余应力检测方法，出现时间较晚。上世纪70年代，Underwood等人开始研究静载压痕周围的唯一场规律，发现残余应力对压痕周围应变的影响规律性[9]。上世纪90年代以来，中科院金属研究所和上海交通大学等开始对动载荷静载作用下压痕周围应力应变场的变化规律进行理论与试验研究。他们通过采用有限元模拟和试验标定方法，初步探讨压痕周围塑性区的大小及其随初始残余应力的变化规律[10-13]。目前，该方法作为非破坏性的静态应变－应力测量和分析的一种重要工具，在材料研究、机械制造、采矿冶金、水利工程、铁道运输、化工设备、船舶制造、航空工业、电力建设等行业应用广泛。如在上海宝冶工程技术有限公司、上海宝钢汽车产品中心、武汉钢铁（集团）公司技术中心、西安交通大学材料学院、哈尔滨工业大学材料学院、水利部金属结构质量检验测试中心和清华大学力学研究所等国内诸多单位成效明显。工程应用结果表明，压痕应变法不仅测试设备相对简单，测试结果准确可靠，而且被测件表面无明显损伤，属于无损应力检测方法[14]。特别对金属表面应力梯度大的残余应力分布测量更有独到之处。

对此，笔者采用压痕应变法[15,16]，实测木工圆锯片[17,18]试件残余应力值，并对各测点结果进行径向和切向残余应力分布分析，在工程领域具有一定实用价值。

1 试验理论阐述

压痕应变法是一种新型残余应力测试方法，它是利用球型压头压入材料表面，通过测量压痕周围的唯一变化情况来计算残余应力[8]。

压痕应变法是采用电阻应变片作为测量用敏感元件，在应变花中心部位采用冲击加载制造压痕以代替钻孔，通过应变仪记录压痕区外弹性区应变增量的变化，从而获得对应于残余应力大小的真实弹性应变，求出残余应力值。该试验因考虑应力超过圆锯片构件屈服点50%且未知主应力方向等情况，拟采用三向应变花进行测量。同时，为得到对称的附加应力场，采用压头直径1.58 mm的硬质合金钢球在锯身测点上制造深度约0.15～0.2 mm的压痕，即将带有钢球的一端垂直置于欲制其压痕的位置（应变花轴线中心），以一定动量冲击支撑杆的另一端。值得一提的是，压痕诱导的叠加应变增量，则由事先粘贴的应变花测取。并且在相同残余应力场中，主应力方向上的球形压痕直径与距压痕中心固定距离处的应变增量成正比。

2 圆锯片试件与仪器

2.1 木工圆锯片

该试验选用编号为Y2和Y5的两块同厂家同批号的木工圆锯片，见图1。其主要参数为：外径300 mm、齿宽3.2 mm、齿厚2.2 mm、内径30 mm、齿数96、最高转速6 800 r/min，且齿形及其尺寸均相同，钢号为日本产SK5。

图1 两种不同锯身减振槽的木工圆锯片试件Fig.1 Two carpentry saw blade specimen of different saw body damping grooves

2.2 KJS-3型压痕法应力测试系统

该系统由压痕制造系统和应力测试系统两部分组成，由中国科学院金属研究所和南京贺普科技有限公司联合制造。其最大测量误差＜15～20 MPa；应变测量精度为1；压痕定点打击对中精度为0.05 mm；压痕尺寸测量精度为0.01 mm；应力计算显示精度为1 MPa；应力测量误差≤20 MPa；压头直径为1.58 mm；球冠压痕直径为1.0～1.2 mm、压痕深度为0.15～0.2 mm。

1）压痕制造系统。

压痕制造系统包括压痕打击装置、永磁式固定底座、对中显微镜三部分，其中压痕打击装置采用弹簧加力、头部镶有直径1/16英寸硬质合金球的机械式冲击装置；对中用显微镜与固定底座结合，用来确定压痕打击的准确位置；固定底座底部镶有高性能永久磁铁，可快速吸附于磁性材料表面，同时能保证压痕打击装置准确定位于应变片上的压痕打击位置，制造出对中精确的压痕。

2）KJS-3型压痕应力测试仪。

压痕应力测试仪采用ARM主板，内嵌Windows CE操作系统，智能化管理，可全软件操作。具有体积小、重量轻、测试方便快捷计算更准确等特点。液晶触摸屏菜单方式简单明了，外接USB口可进行通信及存储。机内带有3点应变自动调零、自动测试、测试数据屏幕显示、贮存、数据处理（将应变值转化为应力值）等功能，特别适合于实验应力分析和现场焊接结构的残余应力无损检测。其量程为±16 000με，分辨率1με，灵敏系数为0～9.99线性可调。

2.3 KFG-1-350-D17-11N30C2型应变花

每块测量用的圆锯片各测点粘贴1片专用应变花（三向），其电阻值为（119.8±0.3）Ω、灵敏系数为（2.0±1）% 。压痕周围弹性区应变变化的正确测试是准确测量残余应力的关键。将三向应变花沿主应力方向粘贴时，可以保证测出的残余应力有较高的准确度[19,20]。

3 测试方法与过程

3.1 测试方法

压痕应变法是通过叠加应力场[20]引起的应变增量计算原始残余应力。其中，在含有残余应力的圆锯片锯身表面，贴上双向应变花，应变栅的方向应尽量与主应力方向一致。该试验测量圆锯片构件的残余应力时采用公共补偿连接法，补偿片连接在补偿两个端子上。通过在应变片的交点中心打击一个压痕，测量其输出的应变值，并用事先在实验室标定得到的计算常数，按胡克定律即可计算出沿应变片方向原始残余应力。

3.2 测试过程[16]

该试验环境温度23 ℃，相对湿度55%，交流220 V/50 Hz电源输入，无强磁场干扰。

1）被测构件表面准备。

根据被测圆锯片构件的应力分析要求及其表面的可操作状态来确定测量位置。每块圆锯片选取0、1、2、3四个测试点，均在圆锯片直径线与同心圆周的交点上，测试点分布示意图见图2。为使表面机械打磨引入的附加应力减至最小，同时便于粘贴应变片，采用100～200#纱布，在圆锯片锯身的打磨区域的两个垂直方向来回打磨，即表面手工打磨处理。

2）应变片粘贴。

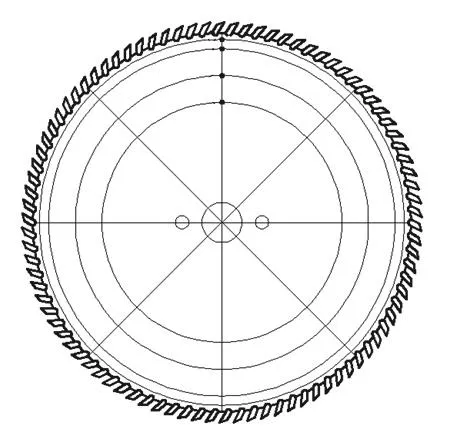
图2 Y2号圆锯片构件残余应力测点分布示意图Fig.2 Schematic diagram of measuring point distribution about number Y2 saw blade specimen residual stress

应变片粘贴质量是残余应力测量结果准确与否的关键，主要过程如下：首先，用干净棉纱蘸上丙酮单向擦拭表面，直至清洁；其次，在准备好的专用二向应变片背面均匀涂抹一层502快干胶，对准测点部位放好，必要时用镊子轻轻移动和触摸应变片调整位置。粘贴时要保证两个垂直的应变栅分别于主应力方向平行和垂直，且胶层应尽量薄。并将聚氯乙烯薄膜放在应变片上方，用拇指滚压1～2 min；再次,10 min左右沿切向轻轻揭起塑料膜。当应变片密实，无任何翘起时，在应变片引出线附近粘贴接线端子。最后，在距离打击点1～2 mm范围内用刀片各划一刀，以切断应变片基片与压痕打击处的联系。

3）制造压痕。

粘贴应变片后1～3 h，进行压痕制造工作，即：第一步，在压痕测试仪的CH1、CH2通道上接入测量用的应变片。CH1、CH2应变值对应仪器屏幕上的径向应变C1、切向应变C2。按“初值”键，观察应变平衡情况。第二步，将对中底座大致以应变片为中心位置，然后插入显微镜，必要时可轻轻移动底座，再通过底座上的调整螺丝微量调整显微镜镜筒，将应变片上的压痕打击点与显微镜中心点调节至重合。第三步，拔出显微镜，将打击杆拉杆拉伸至锁扣相应档位，然后插入底座中。按“应力”键，将初始值归零。

4）正式测量。

在软件上通过新建文件名、参数设置[修正因子0.95，灵敏系数（2.05±1）%等]进入“实时值”界面，点“初值”观察各通道平衡状态，并预热10 min。再点击“应力”，使仪器进入应变采集工作状态，完成击打后再点击“应力”结束采集，此时“实时值”界面显示实时的测量应变值和应力值[21]的计算结果。该试验每测一点，仪器将自动测量、记录、计算和存储有关数据。

图3 圆锯片试件残余应力测试现场Fig.3 Residual stress test of circular saw blade

4 结果与分析

上述Y2、Y5号圆锯片试件测算的应变、应力数据结果如表1所示。其径向和切向残余应力分布见图4、5。

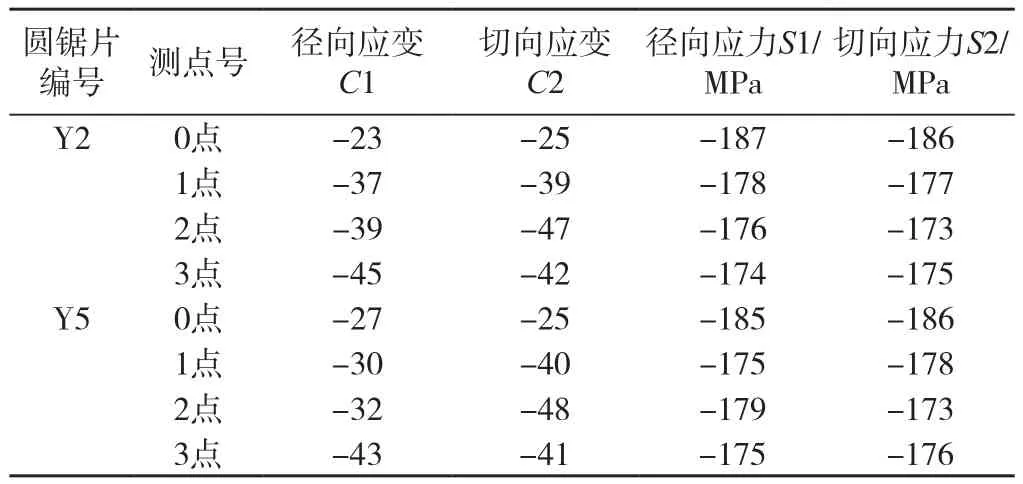
表1 圆锯片试件的应变、应力数据测算表Tab.1 The strain and stress data of circular saw blade

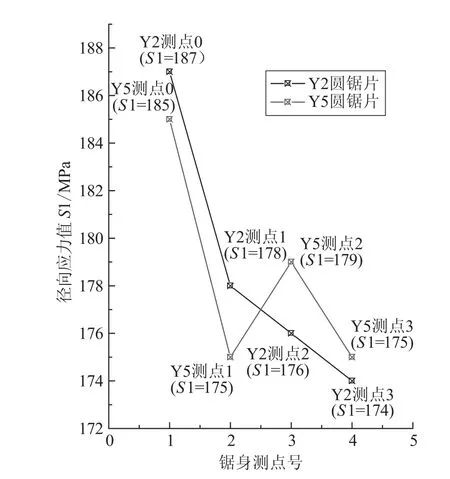
图4 径向残余应力（S1）分布Fig.4 Distribution of radial residual stress (S1)

由图4可知，Y2号圆锯片构件上的0、1、2、3测点的径向残余应力值呈依次降低的趋势，其中0测点值187 MPa为最大，分别高于1测点、2测点和3测点值（最小值）的5.1%、6.3%和7.5%。Y5号圆锯片试件上的0测点径向残余应力值185 MPa为最大，3测点最小；且0测点值高于1测点、2测点和3测点值（最小值）的5.7%、3.4%和5.7%。同理，由图5得知，Y2号圆锯片试件上的0测点的切向应力值186 MPa为最大，分别高于1测点、2测点（最小值）和3测点值的5.1%、7.5%和6.3%。Y5号圆锯片试件上的0测点的切向应力值186 MPa为最大，且0测点值高于1测点、2测点（最小值）和3测点值的4.5%、7.5%和5.7%。

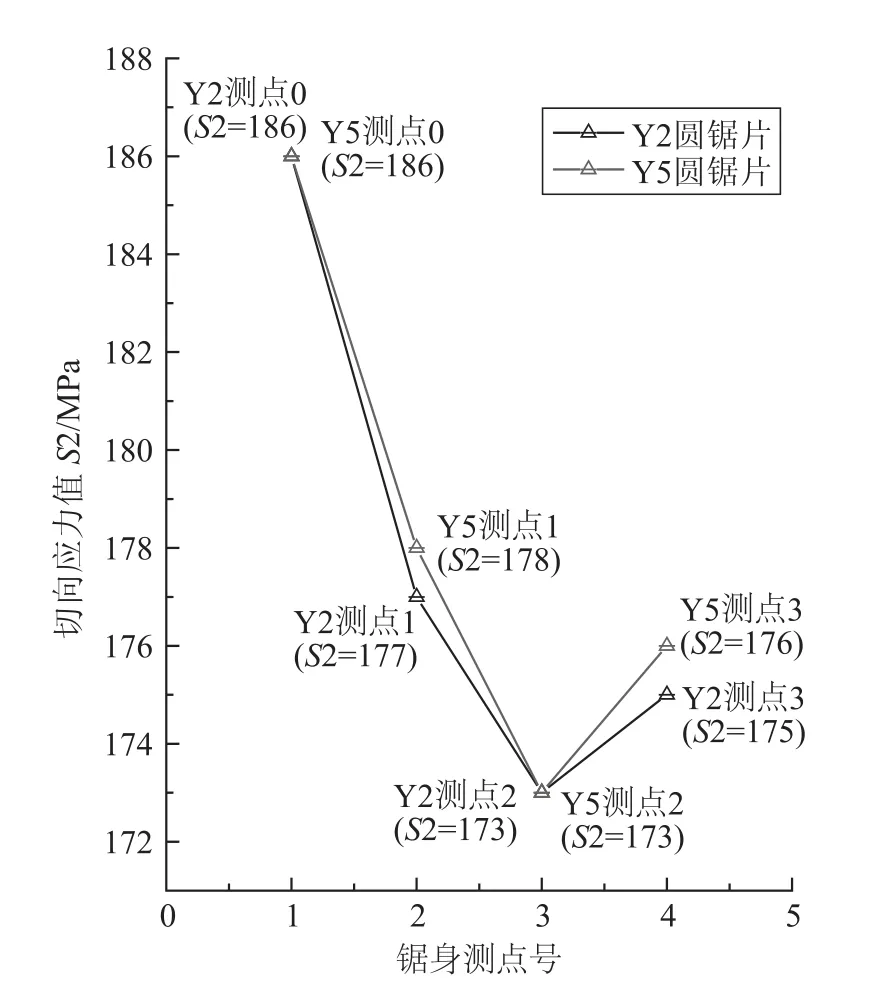
图5 切向残余应力（S2）分布Fig 5 Distribution of tangential residual stress (S2)

上述表明，因0测点靠近锯片的齿根部位，受其齿根应力集中、齿头焊接应力和卸荷槽加工应力等因素影响，致使0测点的径向残余应力值最大。该试验所测的Y2、Y5号两块同条件下的圆锯片构件的相关点径向和切向残余应力值吻合，既说明了该试验结果符合理论的事实，同时反映出该圆锯片构件的生产企业使用的材质好，圆锯片结构设计合理，机加工、热处理、焊接和适张度处理等工艺技术水平较高等实力状况。

5 结论与建议

1）压痕法的应力测量过程简便易行，测量精度较高，无需昂贵的仪器设备。

2）圆锯片锯身上距齿根部位最近测点的残余应力值最大；其锯身上各测点的径向和切向残余应力值一致。对此，圆锯片制造厂家应注重齿形设计与加工及其焊接工艺试验等优化工作。

3）压痕周围弹性区应变变化的正确测试是准确测量残余应力的关键。该压痕法用双向应变花沿圆锯片的主应力方向进行粘贴，且粘贴质量好，可确保测出的圆锯片残余应力值有较高的准确度。

4）该工程中鉴于客观条件的限制，应力测量点数目有限，一定程度上影响了测量的可靠性和概率分析，后续研究将有待开展。

[1] 张占宽,习宝田,程放.球面多点加压适张圆锯片残余应力[J].北京林业大学学报,2009,27(2):111-113.

[2] 冯文鑑.钢结构残余应力测定中应力释放系数的有限元分析[J].福建建筑,2012,165(3):52-54.

[3] 孙渊.预应力下实验标定的盲孔法测试技术[J].上海电机学院学报,2011,14(3):141-145.

[4] 周上祺.X射线衍射分析原理、方法、应用[M].重庆:重庆大学出版社,1991.

[5] 陈玉安,周上祺,韩宪兵.三维残余应力及深度分布的X射线分析和计算[J].重庆大学学报,2002,25(1):40-43.

[6] 孟宪陆,陈怀宁,林泉洪.压痕应变法中压痕周围的应力应变分布规律[J].焊接学报,2008,29(3):109-112.

[7] 曲鹏程,陈怀宁,林泉洪.屈服强度对压痕应变法测量焊接应力中应变增量的影响[J].机械强度,2007,29(6):904-907.

[8] 林丽华,陈立功.用数值分析方法探讨静载压痕残余应力测量方法[C]//第八届全国焊接学术会议论文集(2).北京:机械工业出版社,1997:696-698.

[9] John H Underwood.Residual-stress measurements using surface displacements ayound on indentation[J].Experimental Mechanics,1973,13(5):373-380.

[10] 陈怀宁,林泉洪,陈静,等.冲击压痕法测量残余应力中的塑性区问题[J].焊接学报,2001,22(5):21-23.

[11] 曲鹏程,陈怀宁,林泉洪,等.屈服强度对压痕应变法测量焊接应力中应变增量的影响[J].机械强度,2007,29(6):904-907.

[12] Lin Quanhong,Chen Huaining.Study of measuring residual stresses by impact indentation method[C].Switzerland:Materials Science Forum,2005,490:196-201.

[13] 陈怀宁,林泉洪,曲鹏程.压痕法测量焊接应力中的几个基本问题[C]//第十一次全国焊接学术会议论文集(2).北京:机械工业出版社,2005:116-119.

[14] 刘生,陈怀宁,陈静.未知主应力方向残余应力的压痕应变法测量及其程序设计[J].设计计算,2013,30(2):36-40.

[15] 中华人民共和国国家质量监督检验检疫总局,中国国家标准化管理委员会.GB/T 21680—2008 木工圆锯片尺寸[S].北京:中国标准出版社,2008.

[16] 中华人民共和国国家质量监督检验检疫总局,中国国家标准化管理委员会.GB/T 24179—2009 金属材料 残余应力测定 压痕应变法[S].北京:中国标准出版社,2009.

[17] 姚秉辉.木材加工机械[M].北京:中国林业出版社,1998.

[18] 南京林业大学.木材切削原理与刀具[M].北京:中国林业出版社,1982.

[19] 孟宪陆,陈怀宁,林泉洪,等.压痕应变法中压痕周围应力应变的分布规律[J].焊接学报,2008,29(3):109-112.

[20] 张如一,陆耀桢.实验应力分析[M].北京:机械工业出版社,1981.

[21] 吴雪松,张健,张秀伟.金刚石圆锯片应力计算模型建立及求解[J].大连理工大学学报,2001,41(4):477-479.