基于异质性收敛的中国碳排放强度脱钩效应研究

赵桂梅，陈丽珍，孙华平，赵桂芹

（江苏大学a.财经学院；b.产业经济研究院；c.京江学院，江苏镇江212013）

基于异质性收敛的中国碳排放强度脱钩效应研究

赵桂梅a，b，陈丽珍a，b，孙华平a，b，赵桂芹c

（江苏大学a.财经学院；b.产业经济研究院；c.京江学院，江苏镇江212013）

文章在测算中国30个省区1995-2015年碳排放强度的基础上，通过异质性PS收敛方法确定“俱乐部收敛”类型，解决EKC同质性假设的问题，构建碳排放强度的空间面板数据计量模型，对各类型区域碳排放强度EKC曲线的拐点及峰值时间进行实证检验。研究结果显示：考虑空间相关性与空间异质性后，中国碳排放强度EKC模型的估计结果更加稳健，五种类型区域碳排放强度EKC假设成立；“十三五”期间中国经济增长率为6.5%的目标条件下，模型估计结果进一步证明中国将在2020年实现碳排放强度与经济增长的“脱钩”；中国经济发达的省区已经率先实现碳排放强度的达峰目标，但是如果经济落后的省区不能如期抵达峰值，必将影响全国碳排放峰值的时间和目标。从碳排放强度EKC曲线拐点来看，中国差异化碳减排政策应该根据各类型区域经济增长与碳排放的发展阶段，通过政府引导作用促使碳排放EKC曲线变化更加平缓，保证经济发展的同时分区域有重点地控制并减少碳排放总量，进而确保各省区能够根据地区发展实际科学落实国家节能减排任务；同时，提高资源的利用效率，促进异质性类型区域实现碳排放强度收敛于共同稳态，进而扭转中国经济增长导致环境恶化的不利局面。

碳排放强度；PS收敛模型；EKC空间计量；脱钩效应；差异化碳减排

中国“十三五”规划纲要明确提出碳排放总量与碳排放强度双重约束的减排目标要求，同时要在大气污染防治等环境指标方面取得明显成效。目前，由于中国各省区经济发展水平的巨大差异以及碳排放空间分布呈现非均衡性，中央政府在分配减排任务时会产生较大的区域间利益冲突，减排难度与社会成本将会越来越高。中国碳排放地区差异的演进趋势如何？以及如何在梯度发展模式下实现经济增长和务实减排？对于这些问题进行深入研究，将有利于把握中国省域碳排放的演进规律及变动趋势，以期为中国经济发展与碳减排政策的制定提供参考依据。

一、文献综述

Grossman&Kruege（1991）提出环境库兹涅茨曲线（Environmental Kuznets Curve，简称EKC）揭示经济增长与环境质量演进的“倒U型”变化规律［1］。随后，国内外学者围绕EKC曲线的存在性展开一系列的学术讨论与实证检验。Sanjeev K（2004）采用Lo⁃gistic曲线测算环境退化的发生率，检验EKC曲线的存在性［2］。John A Lista&Craig A Galleta（1999）研究发现基于时间序列数据的EKC曲线不存在，基于截面数据的EKC曲线存在［3］。Jalil A&Mahmud S F（2009）认为中国二氧化碳排放的EKC假设成立［4］。中国学者基于EKC也做了大量的研究。宋涛等（2007）运用DOLS估计方法论证工业污染物排放中人均废气、人均固体废弃物和人均收入之间存在“倒U型”关系［5］。李国志等（2010）持相反的观点，认为中国碳排放不存在EKC曲线，碳排放尚处于单调递增阶段［6］。邓晓兰等（2014）研究支持这一观点，并认为当前处于拐点前的上升期［7］。赵桂梅等（2015）研究发现区域经济增长与环境污染呈“N型”关系，二氧化碳排放处于持续增长状态［8］。沈能等（2016）采用空间效应模型对中国农业增长与污染排放EKC曲线进行实证检验［9］。

中国碳排放何时能达峰不仅是国内经济和社会发展的重要问题，也引起国际能源、气候等相关研究机构的关注。美国能源基金会（The Energy Founda⁃tion，EF）和世界自然基金会（World Wide Fund for Na⁃ture or World Wildlife Fund）在《中国2050年低碳发展之路：能源需求暨碳排放情景分析》报告中指出，在最严苛的“强化低碳”情形下，碳排放有可能在2030年实现达峰［10］。邓柏盛等（2008）利用EKC研究碳排放规律，将碳排放划分为三个阶段，认为中国处于“相对减排”阶段［11］。邓吉祥等（2014）基于能源消费情况，将中国碳排放达峰时间估计为2040年［12］。渠慎宁等（2011）利用STIRPAT模型预测中国达峰时间为2020-2045年［13］。何建坤（2016）认为碳排放强度下降速度既要高于GDP增长速度也要大于能源消费的年增长率是实现中国2030年达峰目标的前提条件［14］。柴麒敏等（2015）利用IAMC方法模拟中国2030年达峰的不同路径，结果表明中国2030年达峰将使经济总量累计偏移3%，提出中国实现达峰目标需要十五年累计减排超过200亿吨［15］。王萱等（2013）研究发现，发达国家碳排放都已跨过峰值点，完成碳排放强度脱钩，目前基本上进入碳排放总量脱钩的绝对减排阶段［16］。

由于中国各省区的要素禀赋等方面存在较大差异，假定所有经济体具有同质性的EKC检验将与实际结果之间存在一定偏差，由此，EKC曲线的检验必须克服同质性假说的问题。韩永辉等（2016）采用聚类分析方法对中国农业污染物排放的EKC曲线进行检验［17］。张成等（2011）通过数据分组方法对中国各地区工业污染物排放的EKC曲线进行检验，进而解决EKC同质性假设的问题［18］。由于不同行政区域污染物排放数据表现出一定空间相关性，即某一区域的经济增长不仅对本区域环境污染产生影响，而且其周边区域污染物排放对本地区环境质量也将产生潜在的影响。EKC实证研究中如果将研究样本仅仅定义为行政边界，忽略环境污染存在的空间效应，将导致推断结论的偏差。鉴于此，在已有文献基础上，本文拓展相关研究：选择碳排放强度作为研究对象，采用异质性收敛方法确定碳排放强度“俱乐部收敛”的类型，同类型区域之间符合EKC的同质性假设。进一步通过空间面板数据模型实证检验各类型区域碳排放强度的空间效应及EKC曲线拐点，揭示中国碳排放强度时空格局动态演进的特征，为政府构建行之有效的低碳经济发展体系以及实现碳减排目标，提供政策分析工具与决策支持。

二、模型设定与数据来源

（一）PS模型的设定

Phillips P C B&Sul D（2007）提出的PS收敛方法不依赖于任何趋势平稳的研究假设，同时能够解决标准单位根检验所无法进行的异质性条件下收敛性检验问题，主要用于分析面板数据的收敛性质［19］。

1.logt检验

设定CIit,i=1,…,K,N;t=1,…K,T为主要研究的面板数据变量，其中N为样本数，T为样本的时间跨度，CIit为碳排放强度，将面板数据logCIit分解成两个部分：

其中，git为系统因素；εit为个体因素。git和εit可以是线性的、非线性的、平稳的或非平稳的。进一步分解为共同性因子部分和异质性因子部分：

其中，ut为共同因子，也即共同性部分；δit为异质性成分。由此，将logyit的收敛性转化为检验δit是否收敛于常数δ。

原假设（H0）：构建δit的半参数模型。公式如下：

其中，δi固定，σi为异质性规模参数，ξit～iid（0，1）；L（t）为一渐变函数，且满足为收敛速度，函数L（t）确保收敛的存在（当α=0时，收敛速度减缓），由此，收敛检验原假设（H0）为：

备择假设（H1）：存在某个i使得δi≠δ和（或）α＜0。

若原假设（H0）成立，则表明全样本收敛，若备择假设（H1）成立，则表明存在部分样本数据不收敛。在原假设（H0）成立的条件下，hit的截面方差表达式为：由此，构建基于回归方程的收敛性检验模型为：

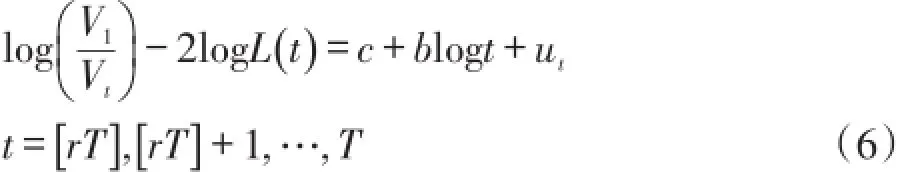
其中，r∈（0，1）①，L（t）=logt。采用稳健的t检验方法，检验b的显著性。函数L（t）的应用确保当α=0时，收敛仍成立。Phillips&Sul（2007，2009）证明收敛的情况下，当t→∞时：

其中，A为正常数。

为了检验面板的收敛性，Phillips和Sul（2007，2009）定义了相对过度参数（Relative Transition Pa⁃rameter），hit表达式如下：

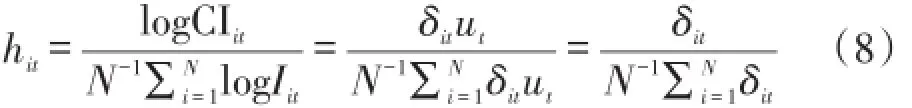
其中，hit为相对过度参数，hit不仅测量某个体相对于其他个体的行为路径，还测量其相对于共同增长路径ut的分离程度；δit为时变特异系数，当δit收敛于常数δ时，则hit收敛于1；ut为共同增长路径。如果hit的横截面方差Vt收敛于零，即当t→∞时有，

Phillips和Sul（2007，2009）通过对横截面方差比进行回归，检验原假设（H0）是否成立：

最后，通过b值和HAC标准差估计方法，进行单边异方差稳健性的t检验，判断不等式零假设α≥0是否成立。

2.类型收敛与合并

根据Phillips P C B&Sul D（2007）提出的PS收敛方法检验样本数据的类型收敛，判断地区间碳排放强度是否存在发散或类型收敛。首先，根据2015年30个省区的碳排放强度数据按照由小到大的顺序排序，确定类型核心组，检验样本数据是否存在类型收敛。选择碳排放强度最靠前的K个地区（2≤K≤N）构建第一个类型核心组，然后检验该类型是否可以构建一个收敛类型。如果t检验结果不能拒绝原假设（H0），则将剩余地区分别逐一并入核心组进行logt检验，通过logt检验结果筛选出所有满足t＞-1.65①的地区，再从中选择t值最大的一个地区与之前两个地区重新组成一组。若最初选取的两个地区构建的第一个类型的原假设（H0）被拒绝，则把碳排放强度排名第一的地区删除，将排名第二和第三的地区确定为第一个类型，并且检验样本数据是否存在收敛。进一步选出t＞c且c≥0（c为临界值）的省区与该收敛类型合并组成新组，并采用logt检验新组是否存在收敛。其次，将没有被选中的地区重新构建为一组并进行logt检验，判断这组是否存在收敛，如果收敛，那这个组就成为另一个收敛类型。如果logt检验结果拒绝收敛原假设（H0），则将这些剩余省区重新进行筛选与合并，进一步检验是否存在其他的收敛类型。如果收敛结果不成立，则表明剩余省区属于发散类型区域。

（二）EKC空间计量模型的设定

在研究经济增长与碳排放强度的EKC回归分析过程中，为消除异方差现象，实际应用中通常在模型两边取对数将其转化为线性回归模型。在用面板数据进行计量分析时，碳排放强度EKC模型表达形式为：

lnCIit=α+β1lnGDPPCit+β2lnZit+ηit+εit（11）

其中，lnCIit为i省t年碳排放强度，lnGDPPCit为人均收入水平，α为常数项，β1，β2为回归系数，ηit为个体效应，εit为随机误差项。lnZit为外生解释变量，包括结构变动、能源强度、人口规模等因素。

Maddison（2006）研究发现使用面板数据可以增加参数估计的有效性［20］。沿用Elmhurst J.P.（2014）提出将时空效应纳入研究体系的空间面板数据计量模型分析框架［21］，基于EKC理论基础，建立中国碳排放强度空间滞后面板数据模型（Spatial Lag Panel Da⁃ta Model，SLPDM）、空间误差面板数据模型（Spatial Error Panel Data Model，SEPDM）和空间杜宾面板数据模型（Spatial Durbin Panel Data Model，SDPDM）三种空间面板数据模型。其中，SLPDM模型设定为：

其中，lnCIit为i省t年碳排放强度；lnGDPPCit为人均收入水平；i表示空间维度，i=1，2，3，…，N；t表示时间维，t=1，2，3，…，T；α表示常数项；εit是随机误差项。β表示相应解释变量的系数，反映解释变量对被解释变量的影响，β1与β2分别是人均GDP及人均GDP平方项的系数：①β1＞0，β2＜0，即碳排放强度与经济增长为“倒U”形关系；②β1＞0，β2＞0，即碳排放强度与经济增长为“U”形关系。根据拐点计算公式ξ=，得出各类型区域碳排放强度拐点的人均GDP水平。lnZit为外生解释变量，包括结构变动、能源强度、人口规模等因素。ρ为空间滞后回归系数，表示空间面板数据的相关性。Wij为地理空间权重矩阵，表达式为：

其中，dij为通过经度、纬度计算的第i个地理空间位置与第j个地理空间位置之间的大圆距离。

为检验各省区间碳排放强度是否存在随机误差冲击的空间溢出效应，设定SEPDM模型为：

其中，jit表示空间自相关误差项；λ表示空间误差回归系数。

进一步设定SDPDM模型为：

其中，α表示常数项；mi为空间特质效应；λt为时间特质效应；δ，θ均为固定的K×1维参数向量；β1，β2，β3为回归系数；当θ=0和θ+δ β=0均被拒绝，则选择SDPDM模型刻画碳排放强度的空间效应。

（三）数据来源

本文研究期间为1995-2015年，由于西藏地区数据缺失，不予以考虑，同时，不将港澳台地区计算在内，最终以中国内地30个省区作为研究对象。由于中国目前没有公布各地区二氧化碳排放量的统计数据，根据IPCC（International Panel on Climate Change，2006）推荐的二氧化碳排放量的估算方法［22］，具体公式为：

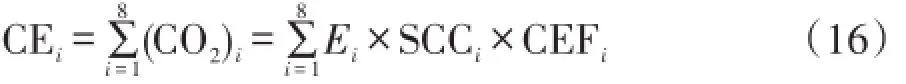
其中，CEi为碳排放量的估算值；i为化石能源的种类，i=1，2，…，8；Ei为化石能源的消费量；SCCi为化石能源的折标煤系数；CEFi为碳排放系数，见表1所列。

表1 化石能源的折标煤系数和碳排放系数

碳排放强度是二氧化碳排放量与GDP经济发展水平之比（万吨/亿元），碳排放强度计算公式为：

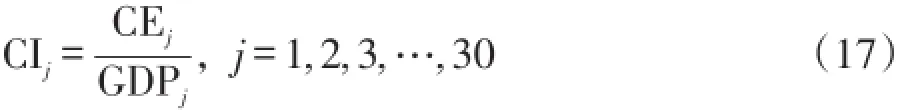
其中，CIj代表第j个省的碳排放强度；CEj代表第j个省的二氧化碳排放量估算值；GDPj表示第j个省的GDP，数据来源于《中国统计年鉴》，并按照2005年不变价格进行调整。

三、实证分析

（一）空间计量模型的检验

根据Anselin L&Florax R J G M（1995）提出的拉格朗日乘数检验（Lagrange Multiplier Test，LM）方法［23］，对中国30个省区碳排放强度的空间效应（依赖性与异质性）进行空间计量检验，结果见表2所列。SLPDM模型中三种空间效应均通过0.05显著性水平的LM检验，SEPDM模型中时空固定效应显著通过0.05显著性水平的LM检验，结合SLPDM模型与SEPDM模型稳健性的检验结果，可以完全拒绝非空间性面板OLS。同时，联合显著性检验似然比（Like⁃lihood Ratio，LR）结果显示空间固定效应（Spatial Fixed Effect）和时间固定效应（Time Fixed Effect）的P值均小于0.01，拒绝非时空固定效应的原假设，进一步选择时空固定效应模型刻画各省区碳排放强度的演进特征。

从空间随机效应（Spatial Random Effects）与时间固定效应（Time Fixed Effect）的Wald和LR检验结果来看，空间随机效应杜宾模型的相关系数在0.01水平下显著，进一步Hausman检验P值也支持选择SD⁃PDM模型，见表3所列。

表2 中国碳排放强度SLPDM与SEPDM的LM检验结果

表3 中国碳排放强度SDPDM的估计结果

中国各省区碳排放强度具有空间外溢效应，研究过程中，如果不考虑客观存在的空间相关性，仅仅采用行政区域划分标准将不能满足EKC的同质性假设，可能会导致估计结果的偏误。

（二）收敛类型的检验

表4为碳排放强度异质性收敛的检验结果。

表4 中国碳排放强度异质性收敛的检验结果

全样本碳排放强度的logt检验结果表明：t值为-36.58＜t-critial=-1.65，整个面板数据收敛的原假设（H0）被拒绝，中国碳排放强度不存在整体收敛。当临界值C*=0时，logt检验结果显示30个省市的碳排放强度存在五个初始收敛类型和一个离散类型，其中，五个初始收敛类型logt检验的系数t值都不显著。进一步类型合并检验发现类型三和类型四合并logt检验的系数t值大于C*临界值外，其他类型合并检验的logt检验系数t值均小于C*临界值，说明类型三和类型四可以合并为一个新的类型，而其他类型不能合并，保持原来类型状态。

（三）各类型区域EKC的估计结果

1.各类型区域EKC的存在性

依据PS收敛及合并检验结果，将中国30个省碳排放强度划分为五种类型区域（其中包含一个发散类型），同类型区域内部的碳排放强度数据满足EKC同质性条件。利用Stata11.0软件对各类型区域碳排放强度EKC参数进行估计，见表5所列。在考虑面板数据的空间相关性后，中国30个省碳排放强度EKC检验中五类区域的经济增长解释变量一次项lnGDP⁃PC及其二次项（lnGDPPC）2的估计系数均达到1%显著水平，EKC估计结果十分稳健。五种类型区域lnGDPPC系数均为正数且（lnGDPPC）2系数均为负数，说明碳排放强度空间面板数据EKC假设成立，进一步计算出各类型区域碳排放强度拐点的人均GDP水平，其中D类型与E类型区域的各省区已经抵达碳排放强度EKC拐点，碳排放强度达到峰值后趋于减少。由于各类型区域在结构变动、能源强度、人口规模等方面的异质性，使得各类型区域之间碳排放强度拐点位置以及达到拐点的时间存在差异，其中A类型区域、B类型区域与C类型区域还未达到拐点，中国整体经济发展位于EKC的左半段。

表5 中国碳排放强度的分组结果及EKC检验

2.各类型区域达峰的时间预期

基于GDP修正对中国经济评价的重要性，根据中国30个省区1995-2015年间人均GDP的实际增长率以及“十三五”期间中国经济增长率为6.5%的目标，采用杨缅昆（2006）提出的GDP修正方法［24-25］基于各类型区域2015年以后的实际人均GDP增长率估算各省区碳排放强度达峰时间，见表6所列。目前，D类型区域中北京（2008年）、上海（2008年）、江苏（2012年）、浙江（2013年）和广东（2015）已经全部达到碳排放强度的拐点；E类型区域的宁夏2014年抵达碳排放强度的拐点。C类型区域包含15个省区，其中天津（2008年）、辽宁（2011年）、山东（2012年）、福建（2012年）、湖北（2015年）和吉林（2015年）抵达碳排放强度的拐点，另外，陕西、湖南、海南3个省区接近碳排放强度的拐点，同时注意到四川、河南、广西、安徽、江西、黑龙江6个省区经济发展位于EKC的左半段且距离EKC拐点较远。B类型区域包括5个省区，其中，内蒙古（2010年）和重庆（2014年）已经达到碳排放强度的拐点，新疆和河北2个省区接近碳排放强度的拐点，但是，甘肃和云南距离EKC拐点较远。A类型区域包括3个省区，其中，青海省（2015年）已经抵达碳排放强度的拐点，山西2015年人均35 094.8元/人，已经接近碳排放强度的拐点，但是，贵州2015年人均GDP为29 938.54元/人，与EKC拐点存在着较大差距。根据中国“十三五”期间预期6.5%的经济增长率，中国碳排放强度将在2020年前抵达EKC拐点，研究结果与林伯强等（2009）提出中国碳排放EKC的理论拐点为2020年左右的结论趋同［26］，但是其估计的拐点（人均GDP 37 170元/人）没有考虑到各省区碳排放强度的异质性收敛及路径性差异。

表6 中国碳排放强度峰值的时间估计

四、研究结论及政策启示

本研究在测算1995-2015年中国碳排放强度省际面板数据的基础上，采用异质性PS收敛法将30个省区划分为五种类型，构建符合EKC的同质性假设的空间面板数据计量模型，对中国碳排放强度EKC曲线进行实证检验及拐点估计。研究结果表明：考虑空间相关性后，中国碳排放强度EKC曲线的估计模型更加稳健，空间杜宾面板数据模型检验结果显示五种类型区域碳排放强度EKC的假设成立。就目前而言，中国碳排放强度整体上仍处于EKC曲线左侧的上升阶段，不同地区碳排放强度拐点及时间路径差异较明显。在“十三五”期间中国经济增长率为6.5%的目标条件下，模型估计结果进一步证明中国将在2020年实现碳排放强度与经济增长的“脱钩”。政策启示如下：

中国梯度发展模式既为中国长期经济发展创造波浪式的后劲与潜力，同时也将延长经济增长的过程。区域间及区域内经济发展的叠加效应决定着中国整体的碳排放达峰目标，不同经济发展阶段的省区实现碳排放强度峰值的时间存在较大差异，峰值前后通常需要相当长的时间积累期。目前，中国经济发达的省区已经率先实现碳排放的达峰目标，但是如果经济落后的省区不能如期抵达峰值，必将影响全国碳排放峰值的时间和目标。因此，中国差异化碳减排政策应该根据各类型区域经济增长与碳排放的发展阶段，促进异质性类型区域实现碳排放强度收敛于稳态，大幅度提高生产率及减排效率，保证经济发展的同时分区域有重点地控制并减少碳排放总量，进而确保各省区能够根据地区发展实际科学落实国家节能减排任务。

从各类型区域以及各省区经济增长与碳排放强度的EKC曲线拐点来看，中国政府应积极采取措施促使碳排放EKC曲线变化更加平缓。根据经济发展基础薄弱以及后发优势特点的省区，通过政府引导作用改变地区碳排放强度EKC的转折点，进而扭转中国经济增长导致环境恶化的不利局面。针对经济发展基础雄厚以及要素禀赋充裕的省区，通过技术创新政策强化新能源开发与利用，逐步推进高碳排放产业发展向“微笑曲线”（Smiling Curve）两端延伸；同时，对于经济发展相对滞后的省区，着力建设低碳排放产业发展模式和低碳基地，实现集约式经济发展发展模式的转型。

注释：

①通过蒙特卡罗模拟实验，建议在T＜50情况下，r=0.3是一个比较合理的选择。

［1］Grossman G M，Krueger A B.Environmental Impacts of a North American Free Trade Agreement［R］.New York：Na⁃tional Bureau of Economic Research，1991.

［2］Sanjeev K S.The Environmental Kuznets Curve（EKC）：a logistic curve？［J］.Applied Economics Letters，2004，11（7）：449-452.

［3］List J A，Gallet C A，Craig A G.The Environmental Kuznets Curve：Does One Size Fit All？［J］.Ecological Eco⁃nomics，1999，31（3）：409-423.

［4］Jalil A，Mahmud S F.Environment Kuznets Curve for CO2，Emissions：A Co-integration Analysis for China［J］.Energy Policy，2009，37（12）：5167-5172.

［5］宋涛，郑挺国，佟连军.基于Weibull函数和Gamma函数的环境污染与经济增长的关系［J］.地理研究，2007，26（3）：569-576.

［6］李国志，李宗植.中国二氧化碳排放的区域差异和影响因素研究［J］.中国人口·资源与环境，2010，20（5）：22-27.

［7］邓晓兰，鄢哲明，武永义.碳排放与经济发展服从倒U型曲线关系吗——对环境库兹涅茨曲线假说的重新解读［J］.财贸经济，2014（2）：19-29.

［8］赵桂梅，陈丽珍.非线性视域下工业污染排放的EKC检验［J］.工业技术经济，2015，34（8）：12-17.

［9］沈能，王艳.中国农业增长与污染排放的EKC曲线检验：以农药投入为例［J］.数理统计与管理，2016，35（4）：614-622.

［10］戴彦德，朱跃中，白泉.中国2050年低碳发展之路——能源需求暨碳排放情景分析［J］.经济研究参考，2010，（26）：2-22.

［11］邓柏盛，宋德勇.我国对外贸易、FDI与环境污染之间关系的研究：1995-2005［J］.国际贸易问题，2008（4）：101-108.

［12］邓吉祥，刘晓，王铮.中国碳排放的区域差异及演变特征分析与因素分解［J］.自然资源学报，2014，29（2）：189-200.

［13］渠慎宁，杨丹辉.中国废弃物温室气体排放及其峰值测算［J］.中国工业经济，2011（11）：37-47.

［14］何建坤.《巴黎协定》新机制及其影响［J］.世界环境，2016，156（1）：16-18.

［15］柴麒敏，徐华清.基于IAMC模型的中国碳排放峰值目标实现路径研究［J］.中国人口资源与环境，2015，25（6）：37-46.

［16］王萱，宋德勇.碳排放阶段划分与国际经验启示［J］.中国人口·资源与环境，2013，23（5）：46-51.

［17］韩永辉，李青，邹建华.基于GPCA模型的中国省域生态文明治理评价研究［J］.数理统计与管理，2016，35（4）：603-613.

［18］张成，史丹，王俊杰.中国碳生产率的潜在改进空间——基于外部环境和内部管理视角［J］.资源科学，2015，37（6）：1218-1229.

［19］Phillips P C B，Sul D.Transition Modeling and Economet⁃ric Convergence Tests［J］.Econometrics，2007，75（6）：1771-1855.

［20］Maddison W P，Knowles L L.Inferring Phylogeny Despite Incomplete Lineage Sorting［J］.Systematic Biology，2006，55（1）：21-30.

［21］Elmhurst J P.Spatial Panel Data Models［M］.Berlin：Springer Berlin Heidelberg.2014：37-93.

［22］Amstel A V.IPCC 2006 Guidelines for National Green⁃house Gas Inventories［M］.Kanagava：The Institute for Global Environmental Strategies，2006.

［23］Anselin L，Florax R J G M.Small Sample Properties of Tests for Spatial Dependence in Regression Models：Some Further Results［M］.Berlin：Springer Berlin Heidelberg. 1995：21-74.

［24］王红茹，钱颖一，贾康，等.GDP修正对中国经济有何影响？［J］.中国经济周刊，2006（1）：70-71.

［25］杨缅昆.绿色GDP和环保活动核算——兼论GDP修正中的方法论问题［J］.统计研究，2000，17（9）：10-13.

［26］林伯强，蒋竺均.中国二氧化碳的环境库兹涅茨曲线预测及影响因素分析［J］.管理世界，2009（4）：27-36.

Research on the Decoupling Effect of Carbon Emissions Intensity in China Based on the Heterogeneity Convergence

ZHAO Gui-meia,b,CHEN Li-zhena,b,SUN Hua-pinga,b,ZHAO Gui-qinc
(a.School of Finance and Economics;b.Institute of Industrial Economics;c.School of Jingjiang,Jiangsu University,Zhenjiang 212013,China)

On the basis of the measurement of 30 provinces’carbon emissions intensity from 1995 to 2015,The paper determines the“club convergence”by the PS test method of heterogeneity convergence,builds up the spatial panel data econometric model,and esti⁃mates empirically the inflection point of EKC curve and the time of peak for the carbon emissions intensity of various regions.During the“13th Five-Year”,if it is estimated that the target of economic growth is up to 6.5%,the results further prove that the overall“decou⁃pling”of carbon emissions intensity in China will be realized by 2020.Some developed provinces and regions have been the first to achieve the goal of the peak of carbon emissions intensity,but if some less-developed provinces cannot reach the peak,that will be bound to the peak time and target of carbon emissions in China.In view of the inflection point of EKC curve,the government should implement some policies to reduce the carbon emissions according to the stage of regional economy and carbon emissions of various types.At the same time,the government should guide and promote carbon emissions EKC curve to be more gentle,control and reduce carbon emissions while marntaining regional economic development,and ensure that each province can implement the national task of energy-saving and emission reduction according to the regional development.Finally,the government should improve the efficiency of resource utilization, promote the heterogeneous region to converge to the common steady state,so as to reverse the condition that the economic growth leading to the deterioration of environment in China.

carbon emissions intensity;PS convergence model;EKC spatial econometric method;decoupling effect;differentiated carbon emissions reduction

F062.1；F062.2

A

1007-5097（2017）04-0097-07

［责任编辑：欧世平］

10.3969/j.issn.1007-5097.2017.04.014

2016-11-29

教育部人文社会科学规划项目（15YJA790006）；江苏省研究生科研创新计划项目（KYZZ_0293）

赵桂梅（1979-），女，黑龙江牡丹江人，讲师，博士研究生，研究方向：生态环境系统工程；

陈丽珍（1957-），女，湖北武汉人，教授，博士生导师，研究方向：国际经济技术合作，国际企业管理；

孙华平（1979-），男，山东兖州人，副教授，博士后，研究方向：国际经济学，产业经济学；

赵桂芹（1976-），女，黑龙江牡丹江人，讲师，经济师，硕士，研究方向：空间统计与计量研究。