引入结构信息的模糊支持向量机

李凯，顾丽凤，张雷

(1.河北大学 计算机科学与技术学院，河北 保定 071002；2.中国联合网络通信有限公司保定市分公司 网络与信息安全部，河北 保定 071051)



引入结构信息的模糊支持向量机

李凯1，顾丽凤1，张雷2

(1.河北大学 计算机科学与技术学院，河北 保定 071002；2.中国联合网络通信有限公司保定市分公司 网络与信息安全部，河北 保定 071051)

模糊支持向量机是在支持向量机的基础上，通过考虑不同样本对支持向量机的作用而提出的一种分类方法，然而，该方法却忽视了给定样本集的结构信息.为此，将样本集中的结构信息引入到模糊支持向量机中，给出了一种结构型模糊支持向量机模型，利用拉格朗日求解方法，将其转换为一个具有约束条件的优化问题，通过求解该对偶问题，获得了结构型模糊支持向量机分类器.实验中选取标准数据集，验证了提出方法的有效性.

支持向量机；模糊支持向量机；结构信息；类内离散度

支持向量机SVM (support vector machine)是由Vapnik等[1]提出的一种机器学习方法，其理论基础是统计学习理论的VC (vapnik chervonenkis)维和结构风险最小化原理.SVM的基本思想是寻找具有最大间隔且将2类样本正确分开的超平面，为此，研究人员对其进行了深入的研究，并提出了很多不同的支持向量机，例如υ-SVM(υ-support vector machines)[2]和LS-SVM(least squares support vector machine)[3].由于支持向量机对噪声或异常点具有较强的敏感性，使得它的训练易产生过拟合现象，从而导致支持向量机的泛化性能降低.为了解决该问题，研究人员提出了模糊支持向量机FSVM (fuzzy support vector machine)[4]，该方法主要将模糊理论引入到支持向量机中，通过考虑不同样本对支持向量机的作用，较好地解决了噪声或异常点对支持向量机的影响.然而，如何确定不同样本的作用，即合理设置样本的模糊隶属度是模糊支持向量机的主要问题.之后，研究人员依据训练样本的分布获得了模糊隶属度的确定方法[5-7]. 另外，一些研究人员通过研究模糊隶属度的确定方法也获得了不同类型的模糊支持向量机[8-10]. 可以看到，对于以上介绍的支持向量机或模糊支持向量机，主要利用了数据集的类间的可分性，但忽视了数据集中类内的结构信息，为此，人们提出了结构支持向量机[11-16]，进一步提高了支持向量机的泛化性能.目前，关于结构支持向量机，人们主要在传统支持向量机的基础上并结合结构信息进行了研究.鉴于模糊支持向量机的影响之深，本文对基于结构信息的模糊支持向量机进行了研究，给出了结构型模糊支持向量机模型，利用拉格朗日方法获得了结构型模糊支持向量机分类器，实验验证了提出方法的有效性.

1 模糊支持向量机

模糊支持向量机是由Lin等[4]提出的一种分类方法，它主要针对数据样本点的重要性不同，将每个数据样本点xi赋予一个合适的模糊隶属值si(0≤si≤1)，以此克服噪声或异常点对支持向量机的影响.为此，在模糊支持向量机中，给定的数据样本集是具有模糊隶属度的一个数据集合.假设X={(x1,y1,s1),(x2,y2,s2),…,(xl,yl,sl)}，其中xi∈Rn，yi∈{+1,-1}，i=1,2,…,l，si是样本xi属于类yi的模糊隶属度.

模糊支持向量机的优化问题如下：

s.t yi(wTxi+b)+ξi≥1，i=1,2,…,l,

(1)

ξi≥0,i=1,2,…,l,

其中ξi是松弛变量，ξ=(ξ1,ξ2,…,ξl)是由松弛变量构成的向量，C是惩罚因子，siξi度量不同变量的重要性.原优化问题(1)的对偶问题为

(2)

0≤αi≤Csi,i=1,2,…,l.

2 结构型模糊支持向量机

2.1 结构型模糊支持向量机模型

在结构型模糊支持向量机SFSVM (structural fuzzy support vector machine)中，不仅寻找具有最大间隔的超平面，而且使得每类具有较小的离散度，为此，将数据集中的结构信息引入到模糊支持向量机中，从而得到结构型模糊支持向量机模型，其优化问题如下：

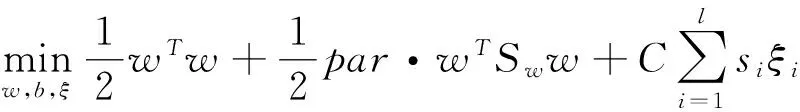
s.t yi(xi·w+b)+ξi≥1,i=1,2,…,l，

(3)

ξi≥0,i=1,2,…,l.

其中par≥0为参数，Sw为给定数据的总类内离散度矩阵.

令I为单位矩阵，∑=par·Sw+I，则(3)进一步变为如下的优化问题：

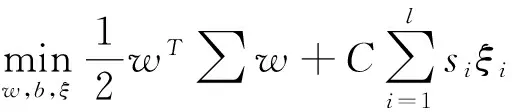
s.t yi(xi·w+b)+ξi≥1,i=1,2,…，l，

(4)

ξi≥0,i=1,2,…,l.

使用拉格朗日方法求解(4)，为此构造如下拉格朗日函数：

(5)

其中α≥0和β≥0为拉格朗日乘子向量，即α=(α1,α2,…,αl) ，β=(β1,β2,…,βl)，函数L的极值应满足如下条件：

(6)

(7)

(8)

将式(6)、(7)和(8)带入(5)，由此得到如下优化问题：

0≤αi≤Csi,i=1,2,…,l.

(9)

可以看到，式(9)为二次规划问题，可以对其直接求解，设获得的解为α*=(α*1,α*2,…,α*l)，将其带入(6)，从而得到最优超平面的法线方向w=∑-1·∑li=1α*iyixi，由此进一步得到如下的决策函数：

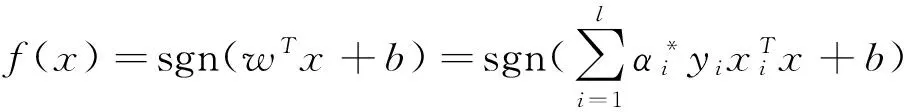
其中b可由K-T条件获得.

2.2 结构信息的获取

假设样本集X中的2类样本构成的集合分别为X+和X-，即X=X+∪X-，m1和m2分别为X+和X-的均值向量，则样本集X的结构信息，即样本集X的类内离散度为

对于样本集X的结构信息，除了使用类内离散度方法获取外，也可利用聚类方法得到. 假设对每类样本聚类的簇数为k个，其聚类结果分别为X+和X-，即

其中X+i和X-i(i=1,2，…，k)分别为对正类样本和负类样本聚类后得到的第i个簇；然后对每个簇X+i和X-i(i=1,2，…，k)，分别计算类内离散度S+i和S-i，从而获得每类的类内离散度S+和S-，即S+=∑ki=1S+i,S-=∑ki=1S-i，则样本集X的结构信息为Sw=S++S-.

可以看到，对于结构信息的获取，给出的2种方法可以统一为使用聚类方法获取样本集的结构信息，也就是说，当聚类方法中的簇数k=1时，则聚类方法获取的结构信息变为直接使用每类的类内离散度方法.

2.3 模糊隶属度的确定方法

对于给定的数据集，如何确定每个样本的隶属度呢？关于该问题，研究人员提出了一些方法.在本文中，使用了Lin等[4]提出的样本隶属度的确定方法，即通过计算每个样本到其类中心的距离来获取样本隶属度，从而减少异常点或噪声对支持向量机的影响.下面给出计算样本模糊隶属度的具体步骤：

1)分别计算正类和负类样本的类中心，设为x+和x-.

3)根据样本类均值和类半径获得每个样本的模糊隶属度

其中，δ>0主要用来避免si=0.

3 实验研究

为了验证提出方法的有效性，实验中选取了11个数据集，分别来自于UCI和Statlog数据库，所有数据集均为2类，具体特性如表1所示.值得说明的是Wine数据集为3类，但在实验中将其转换为2类数据集.在下面的实验中，对于每个数据集，使用随机方法分别抽取90%和70%比例的数据作为训练集，剩余的10%和30%数据作为测试集，实验结果为执行10次实验后得到的平均值，结构信息的获取主要研究了直接计算每类的类内离散度方法，同时与使用聚类方法获取结构信息进行了比较.

为了表明结构信息对支持向量机的影响，实验中选取参数par=9.5进行了研究，随机选取的训练集比例为90%，实验结果如图1所示，其中纵坐标表示10次实验结果的均值和标准差.另外，与模糊支持向量机FSVM的实验结果进行了比较，如图2所示.

表1 数据集的特性

图1 不同数据集的平均正确率与标准差Fig.1 Average accuracy and standard deviation on each data set

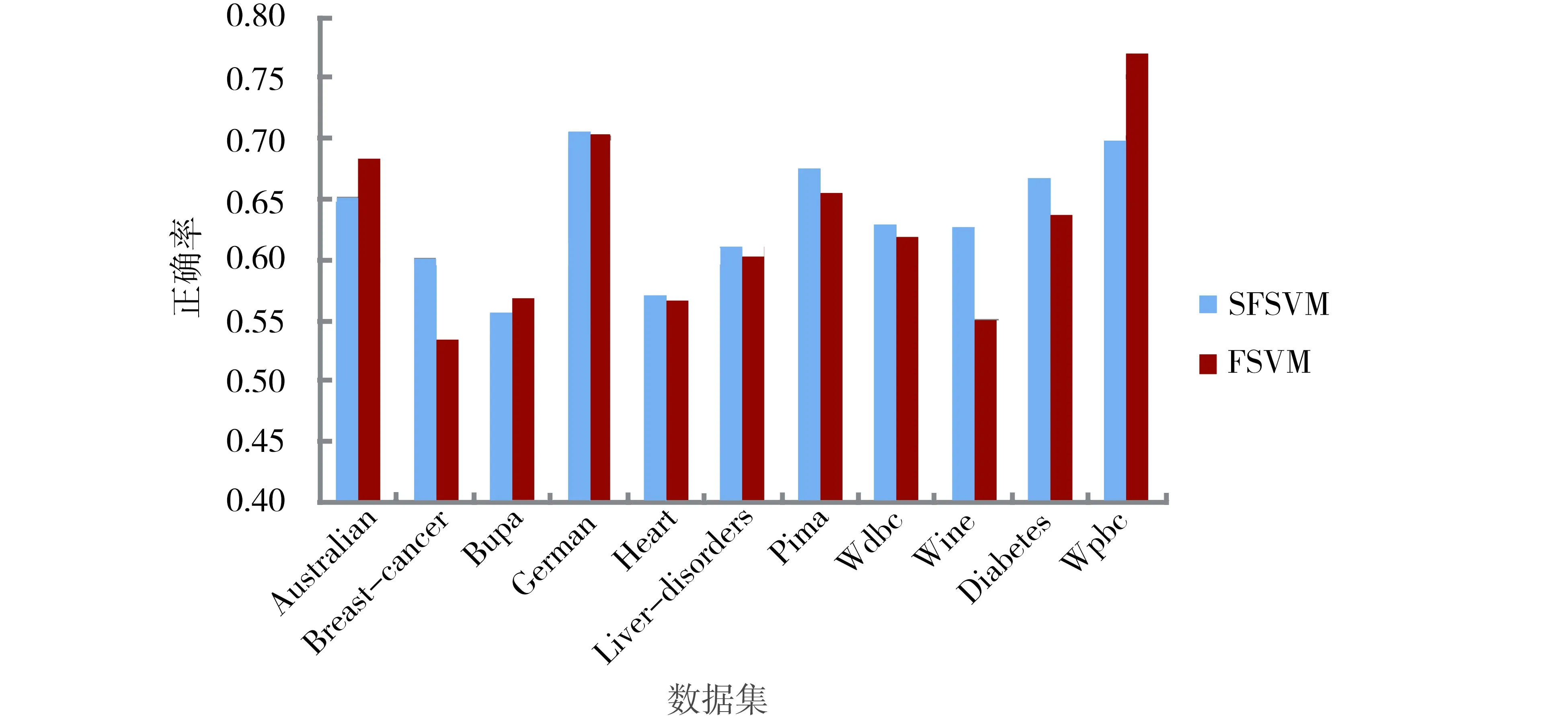
图2 固定参数后的2种不同方法的平均正确率的比较 Fig.2 Comparison of average accuracy for SFSVM and FSVM on each data set with par=9.5

由图2可以看到，在选取的11个数据集中，当选取参数par=9.5时，在8个数据集中，提出的方法SFSVM的性能优于模糊支持向量机FSVM，在另外的3个数据集Australian、Bupa和Wpbc的性能劣于模糊支持向量机FSVM.但是，可以通过合理设置参数par的值，使得提出的方法SFSVM在大部分数据集上优于模糊支持向量机FSVM，为了表明此种情况，对参数par的不同取值进行了实验研究，其取值范围为[3,10]，实验结果如图3与图4所示，其中图3标出了取得较好结果的参数值，图4给出了对应参数的10次运行结果的平均值及FSVM的平均值.可以看到，除了Bupa数据集稍有下降外，在其他数据集都获得了较好的性能.

图3 选取较好参数的每个数据集的平均正确率与标准差Fig.3 Average accuracy and standard deviation on each data set with better parameter value

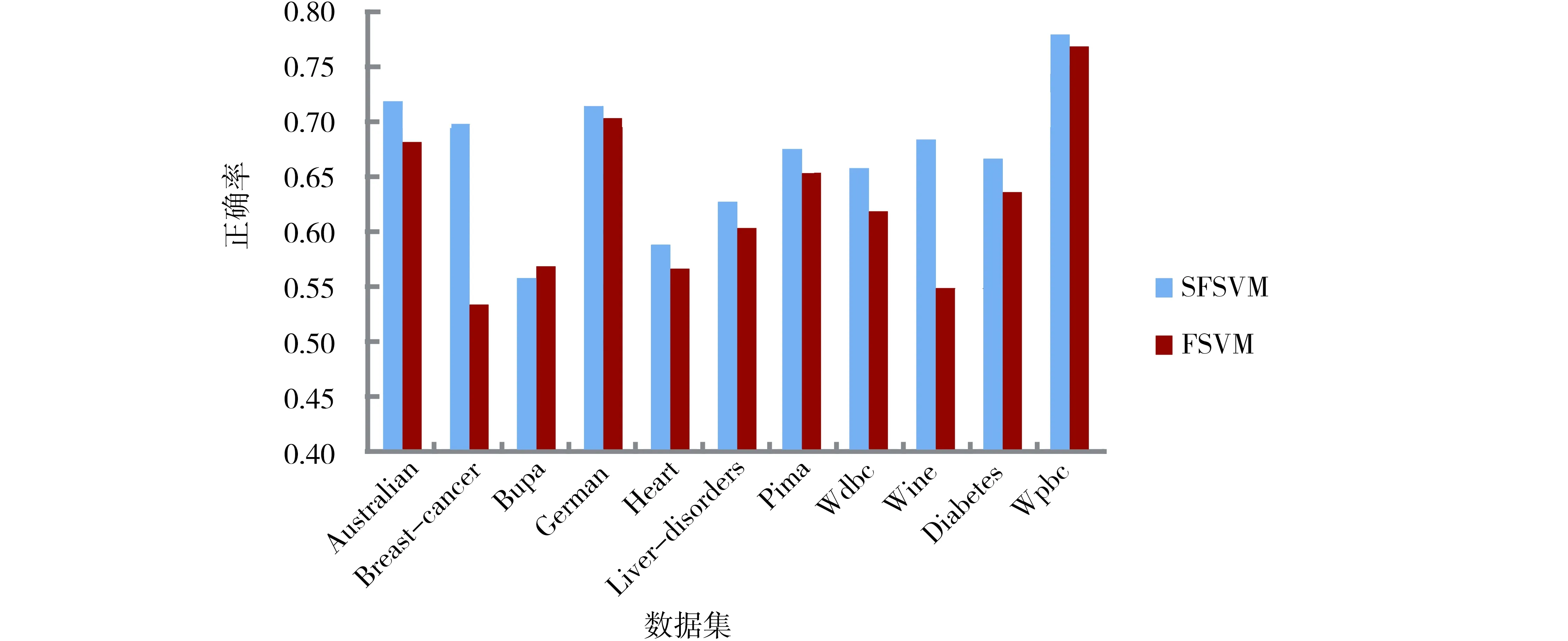
图4 选取较好参数的2种不同方法的平均正确率的比较Fig.4 Comparison of average accuracy for SFSVM and FSVM on each data set with better parameter value

为了表明不同比例的训练数据对分类的影响，针对选取的70%的训练数据进行了实验，参数par的取值分别为4，4.5，5，5.5和6，实验结果如图5和图6所示.由实验结果可以看到，在9个数据集中，提出的方法SFSVM的性能优于模糊支持向量机，而在Bupa和Wine数据集上劣于FSVM，然而对于Wine数据集的性能，2种方法的正确率基本上保持一致.

另外，通过选取90%的数据作为训练集，聚类数目k=3且C=10，利用聚类技术获取数据集的结构信息也进行了实验，同时与FSVM及SFSVM 2种方法进行了比较，为了区分2种不同获取结构信息的方法，用SFSVM-1和SFSVM-2分别表示直接使用类内离散度和聚类技术获取结构信息的SFSVM，实验结果如图7所示. 可以看到，使用结构信息的SFSVM的分类正确率在大部分数据集上优于FSVM，而使用2种方法获取结构信息的分类正确率在不同的数据集上各有千秋，实际上，可以针对不同的数据集，通过设置合理的参数获得较好的分类性能.

图5 SFSVM在不同参数下的平均正确率Fig.5 Average accuracy for SFSVM on each data set with different parameter value

图6 选取较好参数下SFSVM与FSVM的平均正确率比较Fig.6 Comparison of average accuracy for SFSVM and FSVM on each data set with better parameter value

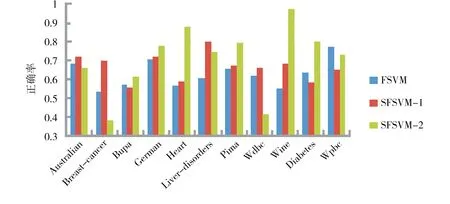
图7 3种不同方法的平均正确率比较Fig.7 Comparison of average accuracy with three different methods

综上所述，在模糊支持向量机中通过引入结构信息，在一定程度上提高了支持向量机的泛化性能，然而，在一些数据集，例如Bupa等，引入结构信息后反而使得支持向量机的性能有所下降，这主要是由于实验中par的参数取值确定为[3,10]，该问题的解决可以通过进一步调整参数值获得较好的性能.

4 结论

模糊支持向量机是在支持向量机的基础上，通过考虑不同样本的作用而提出的一种机器学习方法，然而，该方法只关注了类间的可分性，并未考虑样本集中的结构信息.在本文中，将样本中的结构信息引入到模糊支持向量机中，获得了结构型模糊支持向量机模型，利用拉格朗日方法，将其转换为一个具有约束条件的优化问题，通过求解该对偶问题，从而获得结构型模糊支持向量机分类器.通过选取标准数据集，实验验证了提出方法的有效性，在以后的工作中，进一步研究使用聚类技术方法获取结构信息的模糊支持向量机.

[1] VAPNIK V N. The nature of statistical learning theory [M]. New York:Springer, 1995.

[2] SCHOLKOPF B, SMOLA A J, WILLIAMSON R C, et al. New support vector algorithms [J]. Neural Computation, 2000, 12(5):1207-1245. DOI:10.1162/089976600300015565.

[3] SUYKENS J, VANDEWALLE J. Least squares support vector machine classifiers [J]. Neural Processing Letters, 1999, 9(3):293-300. DOI:10.1023/ A:1018628609742.

[4] LIN C F, WANG S D. Fuzzy support vector machines [J]. IEEE Transaction on Neural Networks, 2002, 13(2):464-471. DOI:10.1109/72.991432.

[5] LIN C F, WANG S D. Fuzzy support vector machines with automatic membership setting [J]. Studies in Fuzziness and Soft Computing, 2005, 177:233-254. DOI:10.1007/10984697_11.

[6] JIANG X F, YI Z, LV J C. Fuzzy SVM with a new fuzzy membership function [J]. Neural Computing and Application, 2006, 15(3-4):268-276. DOI:10.1007/s00521-006-0028-z.

[7] 杨志民.模糊支持向量机及其应用研究[D].北京:中国农业大学, 2005. DOI:10.7666/d.y773695. YANG Z M. Fuzzy support vector machine and its application [D]. Beijing:China Agricultural University, 2005. DOI:10.7666/d.y773695.

[8] SHILTON A, LAI D T H. Iterative fuzzy support vector machine classification[Z]. IEEE International Conference on Fuzzy Systems, London, UK, 2007. DOI:10.1109/FUZZY.2007.4295570.

[9] HONG D H, HWANG C H. Support vector fuzzy regression machines [J]. Fuzzy Sets and System, 2003, 138(2):271-281. DOI:10.1016/S0165-0114(02)00514-6.

[10] YANG X W, ZHANG G Q, LU J. A kernel fuzzy C-means clustering-based fuzzy support vector machine algorithm for classfication problems with outliers or noises [J]. IEEE Transactions on Fuzzy Systems, 2011, 19(1):105-115. DOI:10.1109/TFUZZ.2010.2087382.

[11] YEUNG D, WANG D, NG W, et al. Structured large margin machines:sensitive to data distributions [J]. Machine Learning, 2007, 68(2):171-200. DOI:10.1007/s10994-007-5015-9.

[12] XUE H, CHEN S C, YANG Q. Structural regularized support vector machine:a framework for structural large margin classifier [J]. IEEE Transactions on Neural Networks, 2011, 22(4):573-587. DOI:10.1109/TNN.2011.2108315.

[13] XIONG T, CHERKASSKY V. A combined SVM and LDA approach for classification[Z]. International Joint Conference on Neural Networks, Montreal, Canada, 2005. DOI:10.1109/IJCNN.2005.1556089.

[14] ZHANG L, ZHOU W D. Fisher-regularized support vector machine [J]. Information Sciences, 2016,343-344:79-93. DOI:10.1016/j.ins.2016.01.053.

[15] HOUTHOOFT R, TURCK F D. Integrated inference and learning of neural factors in structural support vector machines[J]. Pattern Recognition, 2016, 59:292-301. DOI:10.1016/j.patcog.2016.03.014.

[16] HOU Q L, ZHEN L, DENG N Y, et al. Novel grouping method-based support vector machine plus for structured data[J]. Neurocomputing, 2016, 211:191-201. DOI:10.1016/j.neucom.2016.03.086.

(责任编辑：孟素兰)

Fuzzy support vector machine based on structural information

LI Kai1, GU Lifeng1，ZHANG Lei2

(1.College of Computer Science and Technology, Hebei University, Baoding 071002, China;2.Department of Network and Information Security,Baoding City Branch of China United Network Communication Corporation Limited,Baoding 071051,China)

By considering the role of different samples on support vector machine, fuzzy support vector machine is presented based on support vector machine. However, it ignores the structural information of the given sample set. To this end, structural information of the given sample set is introduced into fuzzy support vector machine and obtained a structural fuzzy support vector machine model. It is converted to dual problem with quadratic programming using Lagrange method. Through solving this dual problem,the fuzzy support vector machine classifier is obtained. Experimental results in selected standard data sets demonstrate the effectiveness of the proposed method.

support vector machines;fuzzy support vector machine;structure information;within class scatter

10.3969/j.issn.1000-1565.2017.02.013

2016-08-04

国家自然科学基金资助项目(61375075)

李凯 (1963—)，男，河北满城人，河北大学教授，博士，主要从事机器学习、数据挖掘和模式识别研究.E-mail：likai@hbu.edu.cn

TP 319

A

1000-1565(2017)02-0187-07