无温度传感器的金属振动陀螺温度补偿

郑大伟,赵万良,应 俊,成宇翔

(上海航天控制技术研究所 上海惯性工程研究中心,上海 201109)

无温度传感器的金属振动陀螺温度补偿

郑大伟,赵万良,应 俊,成宇翔

(上海航天控制技术研究所 上海惯性工程研究中心,上海 201109)

金属振动陀螺是一种低成本、长寿命的新型简并模谐振陀螺,其结构相对简单,加工相对容易实现。但是,金属材料的温度系数和热膨胀系数大,其受到温度变化的影响明显,温度漂移对器件最终性能的影响较为明显。因此,对金属振动陀螺进行温度补偿,可以显著提高器件性能指标。建立了金属振动陀螺的温度模型,确定环境温度对器件谐振频率和零位偏移的影响关系。研究发现,金属振动陀螺谐振频率的温度系数具有超高线性度,可以替代温度传感器的作用,直接用谐振频率作为温度补偿量的输入。基于温度模型,进一步建立了温度漂移补偿模型,计算金属振动陀螺谐振频率的温度系数和零位偏移的温度关系,并对金属振动陀螺的温度漂移进行补偿。通过实验结果验证,金属振动陀螺谐振频率的温度系数为0.0536 Hz/℃,线性度达3.4×10-6,零位偏移和温度呈二次曲线关系,温度补偿后,金属振动陀螺的随机漂移可降低65%左右。

金属振动陀螺；温度系数；零偏漂移；温度补偿

0 引言

金属振动陀螺是一种基于哥氏效应原理轴对称结构的新型固态波动陀螺。金属振动陀螺具有可靠性高、寿命长、成本低及抗辐照等优点,在惯性导航、制导、姿态稳定控制和惯性测量等领域中具有广阔的应用前景[1-2]。

金属振动陀螺采用弹性合金制作核心谐振子,其加工工艺相对简单、成品率高、易于实现[3]。但是,金属材料本身具有较大的温度系数和热膨胀系数,受环境温度变化影响明显[4]。温度的变化严重影响陀螺的随机漂移和输出零位。因此对于环境温度的稳定控制和归一补偿,可以显著提高陀螺的精度。如果采用温度控制系统使陀螺工作于恒定温度下,这样虽然可以显著提高陀螺的精度,但是也使得器件的成本、能耗、体积明显增加。此时,温度补偿算法将具有明显优势,它可以显著提高陀螺的精度,但对成本、能耗、体积几乎没有影响。

2012年,国防科技大学报道了采用模拟电路系统对杯形振动陀螺进行温度补偿[5]。该系统采用温度传感器敏感空间温度,采用模拟电路系统进行零位补偿,需要进行额外的温度补偿电路系统设计,增加了器件的体积、功耗和复杂度。本文根据杯形金属振动陀螺的特点,设计了一种无温度传感器的数字温度补偿方案,通过对金属振动陀螺温度特性的详细分析,引入合理的温度补偿程序,削弱了温度对金属振动陀螺输出的影响,提高了陀螺漂移等性能指标。

1 结构设计

金属振动陀螺是一种新型固态波动陀螺,由谐振子、压电电极、基座和保护罩组成,如图1所示[6]。谐振子是一个敏感的弹性元件,通过螺钉牢固地安装在基座上。谐振子置于保护罩内,一般保护罩内需要抽真空,使谐振子尽可能少地受到环境干扰,从而稳定的振动。金属振动陀螺基本工作原理为杯形谐振子在谐振状态下产生驻波振动,当谐振子以角速率ω旋转时,驻波振动将受哥氏力作用相对谐振子进动,且驻波振动的振型进动速率与输入角速率成比例关系。

图1 金属振动陀螺组成Fig.1 The composition of MVG

由于表头系统采用真空封装,而温度传感器只能安装在外壳体上,真空环境下温度梯度较大。因此,外壳体的温度并不能完全对应谐振子本身的温度,尤其是不能反映谐振子由于振动发热所引起的额外的温度变化。所以,基于温度传感器的温度补偿方案,通常精度较低,具有一定的进步和提升空间。

2 理论分析

2.1 杯形谐振子谐振频率的温度特性

金属振动陀螺的敏感部件为杯形谐振子,谐振子的谐振频率f0由谐振子的厚度d0、半径R0、材料的杨氏模量E0、密度ρ0等参数决定,具体关系为[7]

(1)

当陀螺器件受到温度变化影响时,会产生两种变化的影响: 1)材料参数的变化,具体体现在材料的杨氏模量E和密度ρ2个参数上；2)结构的尺寸参数,具体是由于热弹性膨胀所引起的体积V和厚度d变化。上述参数随温度T的变化关系可以表示为

E=E0(1+βET)

(2)

d=d0(1+αT)

(3)

V=V0(1+3αT)

(4)

ρ=ρ0/(1+3αT)

(5)

其中,βE为材料杨氏模量的弹性系数,α为材料的热线膨胀系数。材料的泊松比μ对温度不敏感,可认为保持不变。同时,假设材料的热膨胀各向均匀,即谐振子的振动中位线保持不变,谐振子半径R保持不变。则式(1)可以表示为随温度的变化关系

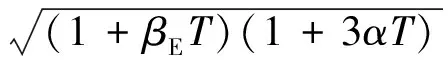
(6)

当温度量变化不大(ΔT<100℃)的情况下,

αT≪1

βET≪1

式(6)可改写为

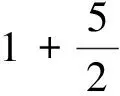
(7)

该陀螺谐振子所采用弹性合金材料的杨氏模量弹性系数βE=0.3×10-6/℃,热线膨胀系数α=6.2×10-6/℃。则计算可得,该陀螺谐振子的频率温度系数βf=15.5×10-6/℃,与材料手册中所示的βf取值范围为10×10-6～20×10-6/℃可对应[8]。

2.2 陀螺零位的温度特性

陀螺零位q0由谐振子的振幅a0、耗散角θ0、频率分裂Δω0等参数决定,具体关系为[9]

(8)

谐振子调平后θ0很小,可将式(8)改写为

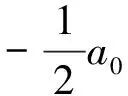
≈-2a0·θ0·Δω0·t

(9)

耗散角θ与频率分裂Δω均随温度线性变化,由于振幅a由电路进行闭环控制,故可认为a不随温度变化。上述参数随温度T的变化关系可以表示为

θ=θ0(1+γ1T)

(10)

Δω=Δω0(1+γ2T)

(11)

其中,γ1为耗散角的温度系数,γ2为频率分裂的温度系数。则式(9)可以表示为随温度的变化关系

q=q0(1+γ1T)(1+γ2T)

=q0(1+γ1T+γ2T+γ1γ2T2)

(12)

当温度量变化不大(ΔT<100℃)的情况下,γ1、γ2较大,其二次项不能忽略。因此,在补偿过程中需要进行零位与温度的二次关系补偿。

2.3 陀螺输出和谐振子谐振频率之间的关系

由2.1节的理论分析可知,谐振子的谐振频率和温度线性相关,具体关系为

f=kT+f0

(13)

其中,f为谐振子的当前谐振频率,f0为谐振子在0℃时的谐振频率,k为谐振子谐振频率的温度系数,T为温度。

由式(13)可得

(14)

由2.2节的理论分析可知,陀螺零位和温度之间成二次关系,具体关系为

q=aT2+bT+c

(15)

其中,q为陀螺零位,a为二次项系数,b为一次项系数,c为常数项。

陀螺补偿后的输出Sout由补偿前的输出Spre、陀螺零位q决定,具体关系为

Sout=Spre-q

(16)

将式(14)、式(15)代入式(16)并化简,可得

(17)

式中,各变量含义前已述及,在此不再赘述。

3 实验验证

3.1 谐振子谐振频率的温度特性测试

本文采用以下测试方案对金属振动陀螺谐振子谐振频率的温度特性进行精确测试。将金属振动陀螺放入图2所示的温控箱中,将温控箱的温度设置为-10℃,1.5h后测得谐振子的谐振频率为3836.9354Hz。

图2 温控箱Fig.2 Temperature control box

用同样的方法分别测得0℃、10℃、20℃、30℃、40℃、50℃时谐振子的谐振频率。用最小二乘法对所得到的数据进行线性拟合,得到谐振子的谐振频率和温度的关系如下

f=0.0536T+3837.4

(18)

原始数据曲线及拟合曲线如图3所示,其谐振子频率的温度系数为0.0536Hz/℃,最大残余误差为0.01Hz。

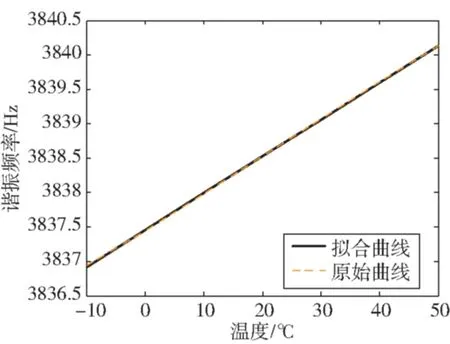
图3 谐振子谐振频率的温度特性Fig.3 The temperature characteristic of resonation frequency

3.2 陀螺零位输出的温度特性测试

在进行3.1节谐振子谐振频率的温度特性精确测试的过程中,采用超高精度数字控制系统[10],同时记录对应温度下陀螺的零位输出。并根据原始记录数据进行二次拟合,其原始数据曲线及拟合曲线如图4所示。

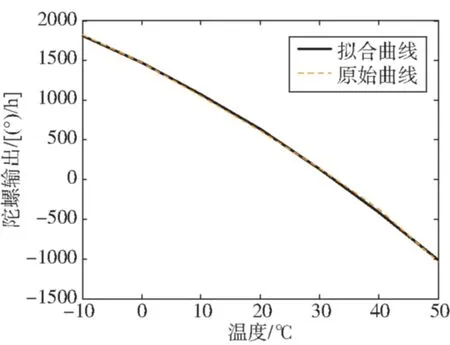
图4 陀螺输出量的温度特性Fig.4 The temperature characteristic of MVG output

由上述测试试验的结果可以看出,陀螺的输出量与温度确实成二次关系。陀螺输出量和温度的关系为

S=-0.25T2-36.92T+1469.5

(19)

陀螺的零位输出温度特性曲线的拟合值与实际测量结果,误差小于1(°)/h。

3.3 金属振动陀螺温度补偿

对陀螺的零位输出进行静态测试,测试时间为6h,按照GJB的测试方法,进行数据记录和计算。将式(18)、式(19)代入式(17)中对陀螺的零位输出进行补偿,补偿前后的陀螺零位输出如图5所示。由图5可以看出,在上述温度补偿后, 6h陀螺的零位输出量趋于稳定,波动明显降低。

图5 陀螺零位输出的补偿前后对比Fig.5 The contrast between MVG bias before compensation and after compensation

根据补偿前后陀螺的零位输出信号,进行随机漂移计算。图6所示为陀螺补偿先后的随机漂移数据曲线。

图6 陀螺随机漂移补偿前后对比Fig.6 The contrast between MVG bias drift before compensation and after compensation

由图6可知,加入温度补偿后,陀螺的零偏稳定性得到较大改善,随机漂移从3(°)/h左右降低至1(°)/h左右,性能提高3倍左右。

4 结论

本文建立了金属振动陀螺的温度模型,确定了环境温度对器件谐振频率和零位偏移的影响关系。研究发现,金属振动陀螺谐振频率可以替代温度传感器的作用,直接用谐振频率来换算得到温度。基于温度模型,进一步建立了温度漂移的二次补偿模型,计算金属振动陀螺谐振频率和零位输出的温度系数,并对金属振动陀螺的零位输出漂移进行温度补偿。温度补偿后,金属振动陀螺的随机漂移从3(°)/h降低到1(°)/h,性能提高了3倍左右。

[1] 周鑫, 吴宇列, 陈志华, 等.高灵敏度圆柱壳体振动陀螺的研究[J]. 传感技术学报, 2013, 26(9): 1206-1212.

[2]OkonIM,SimonenkoDV,BarabashovAS.Sensingelementofcoriolisforcegyroscope[P].U.S.Patent: 0154542A1, 2010: 2-4.

[3]ChengY,ZhengD,LiuR,etal.Orthogonalcompensationoptimizationdesignofpiezoelectricdegeneratedmoderesonantgyroscopes[C]//Proceedingsof2016ChinaInternationalConferenceonInertialTechnologyandNavigation, 2016, 11: 184-188.

[4] 陶溢. 杯形波动陀螺关键技术研究[D]. 长沙：国防科学技术大学, 2011: 105-123.

[5] 张勇猛, 吴宇列, 席翔, 等. 杯形陀螺的温度性能与补偿方法研究[J]. 传感技术学报, 2012,25(9) : 1230-1235.

[6] 谢笛.杯形波动陀螺数字化测控技术研究[D]. 长沙：国防科学技术大学, 2011: 13-15.

[7] 刘宇. 固态振动陀螺与导航技术[M]. 北京： 中国宇航出版社, 2010: 136-174.

[8] 宋键朗,杨奋为,袁文彬,等.材料手册(金属)[M]. 上海： 中国航天科技集团公司第八研究院, 2007: 371-378.

[9] 马特维耶夫. 固体波动陀螺[M]. 杨亚非, 赵辉,译. 北京： 国防工业出版社, 2009: 51-76.

[10]ZhaoW,LiuR,WangW,etal.Ultra-precisedigitalcontrolcircuitsofhemisphericalresonantgyroscopes[C].Proceedingsof2016ChinaInternationalConferenceonInertialTechnologyandNavigation, 2016, 11: 177-183.

Temperature Compensation of the Metallic Vibratory Gyroscopes (MVG) without Temperature Sensors

ZHENG Da-wei, ZHAO Wan-liang, YING Jun, CHENG Yu-xiang

(Shanghai Institute of Spaceflight Control Technology, Shanghai Engineer Research Center of Inertia, Shanghai 201109,China)

The metallic vibratory gyroscope (MVG) is a novel degenerated mode resonant gyroscope with a low cost and long life, which has a simple structure and is accessible to machine. As the metal materials have a large temperature coefficient and thermal expansivity, the temperature has an evident effect on the bias drift of the devices. Thus, the temperature compensating of the MVG could improve the gyroscope’s performance significantly. This paper finds a temperature model of the MVG, to establish the relationship between the resonator frequency, bias and the environment temperature. The model shows that the MVG has a quite high temperature coefficient linearity about the resonation frequency, which makes the resonation frequency could be inputted as a compensating value and replaces the temperature sensors. Based on the temperature model of the MVG, a temperature compensating model is built to calculate the temperature coefficient of the resonation frequency and the temperature sensitivity of the bias. Then, the bias drift of the MVG, caused by the temperature, is compensated. The experiment results show that the device has a temperature coefficient of the resonation frequency of 0.0536 Hz/℃, with a linearity of 3.4×10-6. The bias drift reaches a quadratic curve relationship with the temperature. This compensation method decreases the bias drift of the MVG by about 65%.

Metallic Vibratory Gyroscope; Temperature coefficient; Bias drift; Temperature compensation

2017-01-18；

2017-02-20

上海市青年科技英才扬帆计划(16YF1405100)

郑大伟(1986-),男,助理工程师,主要从事固体波动陀螺方面的研究。E-mail:zdwjs2009@163.com

10.19306/j.cnki.2095-8110.2017.02.016

U666.12

A

2095-8110(2017)02-0093-05