微玻璃半球壳体谐振子的设计、制备与表征

罗 斌,尚金堂

(东南大学电子科学与工程学院,南京 210096)

微玻璃半球壳体谐振子的设计、制备与表征

罗 斌,尚金堂

(东南大学电子科学与工程学院,南京 210096)

近年来美国国防高级研究计划局大力推进三维壳体谐振陀螺(尤其是高性能半球谐振陀螺)的微型化,以实现惯导级性能的微机械振动陀螺。提出发泡法制备直径小于1cm的微壳体谐振子,利用发泡剂在高温下释放气体,使软化后的玻璃在气压差和表面张力的作用下形成三维轴对称壳体。大气环境下多普勒测振仪的测试结果表明,利用发泡法制备的微壳体谐振子的酒杯二阶模态的谐振频率为11kHz,频率分裂值为72Hz,相对裂解值为0.65%,相应的品质因子Q值约为970和1127。发泡法有望提供一种低成本、高性能微壳体谐振子的制备方法。

壳体谐振陀螺；半球谐振陀螺；半球谐振子；发泡法；微壳体谐振子

0 引言

微机械振动陀螺作为哥式振动陀螺的一类扩展,其体积、质量、成本相对于传统精密机械加工制备的哥式振动陀螺而言大幅降低,但性能相对较差。壳体谐振陀螺,尤其是半球谐振陀螺性能优越,近年来其微型化备受关注。2010年,美国国防高级研究计划局开始启动微速率积分陀螺项目,多家公司、实验室和高校相继开始研制微壳体谐振子,特别关注基于半球壳等三维轴对称壳体结构的振动式陀螺的微型化[1]。这些单位的研究大体可分为如下两类。

第一类采用以MEMS 体硅工艺和表面牺牲层工艺为主的技术制备微壳体谐振子[2-6],结构材料为二氧化硅、金刚石或者多晶硅等；这类技术目前面临的主要问题是受MEMS 工艺相对精度的限制,形状和尺寸控制精度不高,表面粗糙度较大,结构对称性相对较差,从而导致谐振子性能不高。第二类利用玻璃吹制技术、玻璃模具成型技术等新型三维成型技术制备微壳体谐振子[7-9],材料为玻璃或者金属玻璃等无定形材料,所制备的结构对称性较高,表面更光滑；而第二类技术的主要问题在于,由于结构材料为玻璃类材料,玻璃的加工难度较大,电极往往不能与谐振子一体成型,后续的器件组装和真空封装有一定的难度。

本文首先从理论出发给出微壳体谐振子合适的工作频率范围,并借助仿真得到初步设计的尺寸范围,然后简要介绍发泡法制备微壳体谐振子的过程,最后给出谐振子初步表征的实验结果。

1 仿真与设计

本节从理论上给出微壳体谐振子合适的工作频率范围,并从仿真的角度选取初步设计的谐振子尺寸范围。

1.1 频率设计

在电极施加作用力维持谐振子振动的幅度和形状时总会有一些幅度、方向和相位误差,这些误差主要来源于电路和驱动器缺陷。对于给定电路和驱动器,由于振幅控制而引起的漂移误差De可以表示为[10]

(1)

其中,τ为时间衰减常数,f为工作频率,Q为工作模态的品质因子,ε为电路和驱动器的控制精度,ε按级别可分为：

1×10-3级：一般。

1×10-4级：复杂。

1×10-5级：高性能/高稳定性。

1×10-6级：极度复杂,特殊用途。

宏观精密机械加工的半球谐振子工作频率范围通常在2～8kHz。法国萨甘安全防护公司的半球谐振陀螺REGYS 20性能优于0.01(°)/h[10],美国诺斯洛普格鲁门公司的半球谐振陀螺HRG 130P性能优于0.001(°)/h[11-12],国内半球谐振陀螺性能也已达到甚至优于0.01(°)/h[12-13]。这里给出谐振子合适的工作频率范围。假设谐振子的Q值能达到10000000,图1所示为不同控制精度下壳体谐振子工作频率对漂移误差的影响。从图1中可以看出,在控制精度达到1×10-5级别的情况下,要获得优于0.01(°)/h 的性能,壳体谐振子的谐振频率应小于15kHz。振动陀螺要达到惯导级性能：

1)控制精度达到1×10-5级别时：谐振频率为10kHz,谐振子Q值大于7000000即可；

2)控制精度达到1×10-6级别时：谐振子Q值10000000时,谐振频率100kHz也可满足要求。

为降低外界振动对谐振子的干扰,同时降低对电路和驱动器的要求,微壳体谐振子的工作频率建议设计在5～15kHz的范围内。

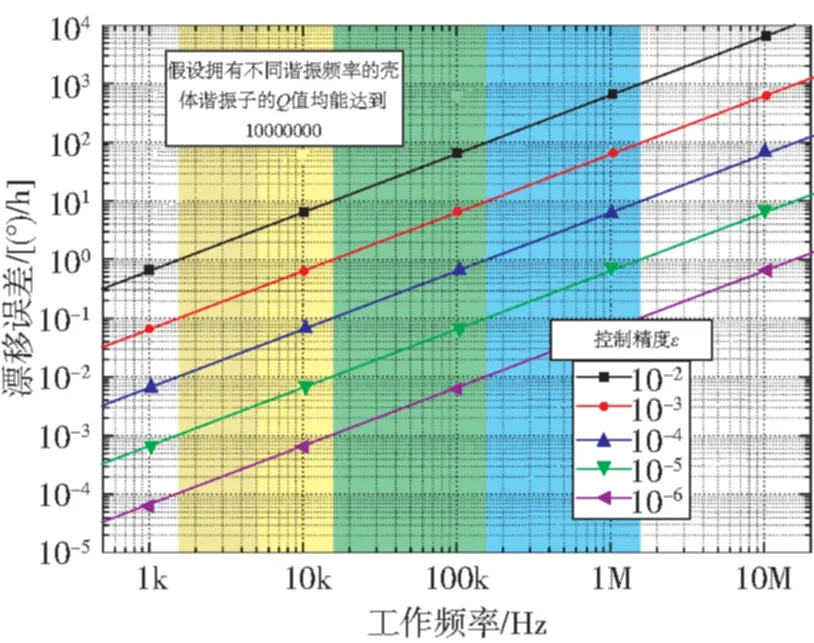
图1 电路和驱动器的控制精度和工作频率对漂移误差的影响(假设拥有不同工作频率的壳体谐振子Q值均能达到10000000)Fig.1 Drift error depending on Q-factor (assuming Q=10million here), working frequency and control accuracy

1.2 仿真分析

ANSYS仿真谐振子谐振频率过程中采用的材料参数为：杨氏模量E=64GPa,密度ρ=2.23g/cm3,泊松比ν=0.22。网格划分采用四边形划分截面然后旋转形成,高质量的网格划分可以保证简并模态间的频率差在1×10-5Hz以下,低质量的网格划分容易导致简并模态间产生几十甚至上百赫兹的频率差。

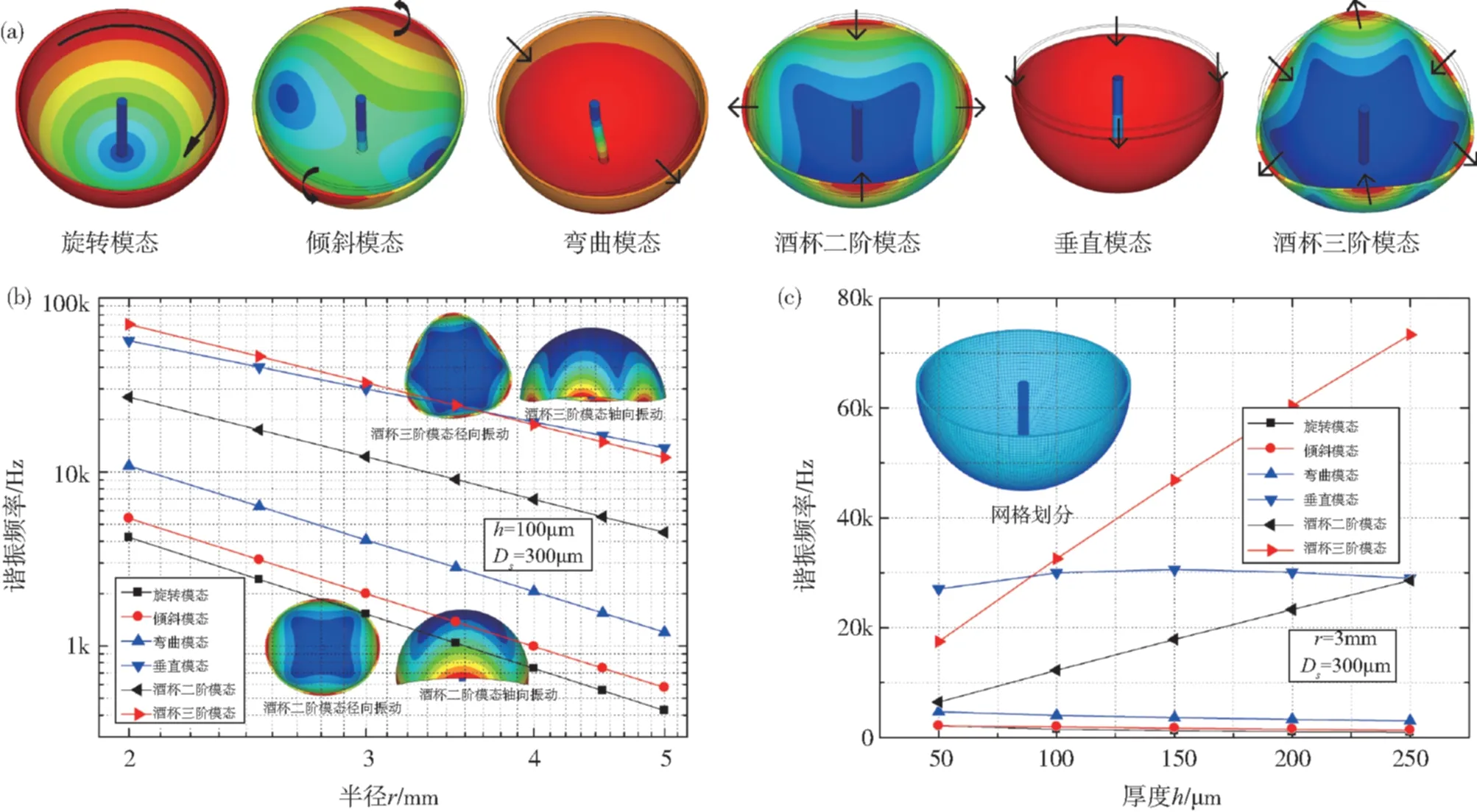
图2 ANSYS 15.0仿真结果：(a) 半球谐振子的主要振型(或模态)；(b) 半球谐振子谐振频率与壳体半径的关系(插图：酒杯二阶、三阶模态径向和轴向振动图)；(c) 半球谐振子谐振频率与壳体厚度的关系(插图：简化后的网格划分示意图)Fig.2 Simulation results: (a) Main mode shapes of a complete hemispherical shell resonator； (b) The relation of resonant frequencies with the shell radius (Insets: in-plane and out-of-plane vibratory displacement of wineglass mode n=2, 3)； (c) The dependence of resonant frequencies on the shell thickness (Insets: simplified meshing of a complete hemispherical shell resonator)

由图2可以看出,当选择工作频率大约在10kHz左右的半球谐振子的尺寸时,对于厚度100μm,选用半径在2.5～4.5mm左右的微壳体谐振子；对于半径3mm,选用厚度在50～150μm的微壳体谐振子。柱子直径Ds对酒杯模态影响不大,但对其他模态影响较大；在选择尺寸时,需要避免酒杯二阶模态与其他模态耦合。为保证合适的谐振频率,如若选用直径较小的微壳体谐振子,则需减小壳体的厚度,这就意味着有效质量的降低,不利于降低微壳体谐振子的热机械噪声[15]。对于上述尺寸选用半径3mm作为初期设计方案。

2 工艺制备

发泡法利用发泡剂在高温下释放气体迅速增加腔室里的气压[16-17],软化后的玻璃在表面张力的作用下形成低表面粗糙度的三维轴对称壳体。发泡法制备微壳体谐振子的工艺步骤主要包括[18-19]：利用激光钻孔或刻蚀技术在衬底圆片形成带柱子的腔室,在腔室中加入发泡剂,然后在衬底圆片上键合玻璃圆片,将键合后的圆片放入加热炉中,升温高于玻璃的软化点,玻璃软化后在表面张力的作用下形成微壳体谐振子。初期实验中衬底圆片采用500μm厚的硅圆片,玻璃圆片采用500μm厚的BF33玻璃圆片。

发泡法制备的微壳体谐振子表面粗糙度在亚纳米级别[18],图3所示为利用发泡法制备出的直径6mm的低深宽比(高度与半径之比)的微壳体谐振子[19]。图4所示为一个低深宽比的微壳体谐振子截面扫描电镜图,微壳体谐振子的深宽比主要由加入的发泡剂的量决定；图4中可以看到激光钻孔后腔底的高低起伏形貌,加入的发泡剂在这种形貌下不易移动。硅柱的尺寸将影响微壳体谐振子柱子的尺寸和形状,第2节中设计时柱子的尺寸选择原则是基于避免与其他模态耦合,实验中腔中硅柱直径D的设计范围在800μm～1.5mm。

图3 直径6mm低深宽比的微壳体谐振子[19]Fig.3 A low aspect-ratio micro shell resonator with 6mm-diameter

图4 微壳体谐振子截面的扫描电镜图Fig.4 Cross-sectional SEM view of a micro shell resonator

3 测试表征

为了研究微壳体谐振子的频率特性,利用压电陶瓷激励谐振子,在大气环境和室温下采用激光多普勒测振仪的单点模式测试一个直径6mm的微半球壳体谐振子的边缘。测试得到的谐振子的频率特性如图5所示,谐振频率点有1.34kHz、3.44kHz、10.96kHz、11.04kHz、19.74kHz、31.68kHz、31.76kHz。为了确定酒杯二阶模态,以24°角度差测试了谐振子边缘的一周振动,测试结果如图6所示,确定了2个酒杯二阶模态谐振频率为10.96kHz和11.04kHz。

图5 激光多普勒测振仪单点模式扫频测试结果(插图：测试的直径6mm的近半球壳体谐振子)Fig.5 Resonant frequencies of the shell obtained from Laser Doppler Vibrometer using single point mode (Inserts: a near-hemispherical shell resonator with 6mm diameter)

图6 2个简并酒杯二阶模态下壳体边缘振动速度测试结果Fig.6 Measured velocity along the rim of the shell at two degenerate n=2 wineglass modes

为了获取确切的本征频率分裂值,利用压电陶瓷固定频率激励,大气环境下测试谐振子边缘的振动,实验结果如图7所示,本征频率分裂值为72Hz,相对裂解值0.65%,利用洛伦兹拟合得到相应的Q值分别为970和1127。目前较大的频率分裂表明谐振子对称性有待提高,原因在于包括成型过程各工艺参数导致的谐振子质量不均匀。频率裂解主要来源于物理尺寸参数方面,如半径、厚度的四次谐波分量[20-21]；另一个影响方面包括谐振子密度、杨氏模量、泊松比的四次谐波分量[21-22]。从多次实验发现主要原因在于成型过程谐振子的不对称,这种不对称来源于温度场不均导致软化后的玻璃的黏度不均匀,黏度不均匀导致成型过程中结构的不对称,主要表现在半径和厚度两个方面的不对称。目前阶段,能量损耗主要有空气损耗和结构不对称带来的锚区损耗。为了获取高性能微壳体谐振子,应采用低热膨胀材料,减小谐振子不对称性,改进设计减小锚区损耗。

4 结论

本文提出并成功采用发泡法制备了微玻璃壳体谐振子。通过理论和仿真,给出了微壳体谐振子合适的工作频率范围和尺寸范围；并对发泡法制备出的直径为6mm的微玻璃壳体谐振子进行了初步的测试。空气环境下多普勒测振仪的测试结果表明,利用发泡法制备的微壳体谐振子的二阶酒杯模态的谐振频率为11kHz,频率分裂值为72Hz,相对裂解值为0.65%,相应的品质因子Q值约为970和1127,如图7所示。较大的本征频率分裂表明壳体结构设计和对称性控制有待于进一步加强。

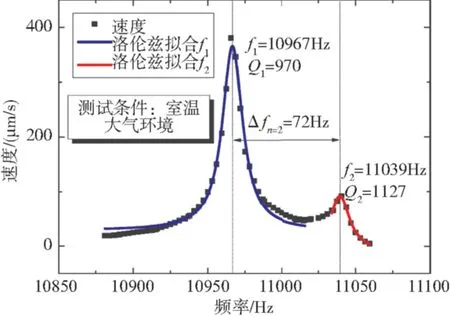
图7 室温和大气压下酒杯二阶模态的本征频率分裂测试结果Fig.7 Frequency split between n=2 wineglass modes measured at atmospheric pressure and at room temperature

为获取高性能微壳体谐振子,应提高壳体的对称性和降低壳体振动的能量损耗。下一步研究重点主要集中在微壳体谐振子工艺制备的控制与优化、微壳体谐振子结构的控制与设计,以及电极制备工艺[23]、器件组装和真空封装等方面。

附录

图8 半球谐振子的截面示意图：Ds为柱子直径,R为中曲面半径,h为壳体厚度,φ0和φf为边界角Fig.8 Cross-sectional view of the hemispherical shell with a stem: Ds is the stem diameter, R is the radius of the shell middle surface, h is the shell thickness, φ0 and φf are boundary angles

(2)

其中,I(n,h)、J(n,h)与酒杯模态的阶数n和壳体的厚度h相关：

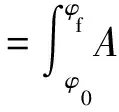
(3)

(4)

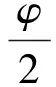
(5)

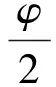
(6)

在式(2)～式(6)中,n为酒杯模态的阶数；E为壳体材料的杨氏模量；υ为泊松比；ρ为材料密度；h(φ)为壳体厚度,与角度φ相关。

当壳体的厚度不随角度φ变化时,酒杯模态的谐振频率可简化为

(7)

(8)

其中,初始角φ0根据图8可由式(9)给出

φ0=arcsin[Ds/(2R-h)]

(9)

对于壳体厚度均匀的半球谐振子,谐振子的酒杯模态的谐振频率与壳体厚度h成正比,与半径R的平方成反比。

为了大致了解边界角φ0、φf对I(n,h)、J(n,h)的影响,边界角的初始值设为φ0=0°,φf=90°,然后改变一个边界角,公式计算出的I(n)、J(n)值如图9所示。当初始角小于15°时,I(n)、J(n)值随初始角的变化较小,实际设计时初始角的大小也在这个范围；当变化的参数为终角时,由图9可以看出,I(n)、J(n)斜率变化较大,尤其当终角接近90°时,这表明终角对谐振频率的影响比初始角的影响大,这种结果可能归结于终角的变化带来谐振子有效质量的明显变化。初始角对酒杯模态谐振频率的影响较小,但对其他模态影响较大,设计时也需选用合适的值。

致谢 感谢卢晨钺在仿真和理论计算方面给予的帮助和支持。

[1] Keller J. DARPA to develop microscale navigational gyro for guided munitions and handheld devices [J]. Military and Aerospace Electronics, 2010, 21(6): 12.

[2] Shao P, Sorenson L D, Gao X, et al. Wineglass-on-a-chip[C]. Proceedings of the Solid-State Sensors, Actuators and Microsystems Workshop (Hilton Head 2012). Hilton Head, SC, USA, 2012: 3-7.

[3] Taheri-Tehrani P, Su T, Heidari A, et al. Microscale diamond hemispherical resonator gyroscope[C]. Proceedings of the Solid-State Sensors, Actuators and Microsystems Workshop (Hilton Head 2014). Hilton Head, SC, USA, 2014: 289-292.

[4] Bernstein J, Bancu M, Cook E, et al. Diamond hemispherical resonator fabrication by isotropic glass etch[C]. Proceedings of the Solid-State Sensors, Actuators and Microsystems Workshop (Hilton Head 2014). Hilton Head, SC, USA, 2014: 273-276.

[5] Vafanejad A, Kim E S. Effect of diaphragm perforation on quality factor of hemispherical resonator gyroscope[C]. 2015 18thInternational Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), 2015: 27-30.

[6] Gray J M, Houlton J P, Gertsch J C, et al. Hemispherical micro-resonators from atomic layer deposition [J]. Journal of Micromechanics and Microengineering, 2014, 24(12): 125028.

[7] Senkal D, Ahamed M J, Trusov A A, et al. High temperature micro-glassblowing process demonstrated on fused quartz and ULE TSG [J]. Sensors and Actuators A: Physical, 2013, 201(5): 525-531.

[8] Cho J Y, Yan J, Gregory J A, et al. 3-dimensional blow torch-molding of fused silica microstructures [J]. Journal of Microelectromechanical Systems, 2013, 22(6): 1276-1284.

[9] Kanik M, Bordeenithikasem P, Schroers J, et al. Microscale three-dimensional hemispherical shell resonators fabricated from metallic glass[C]. 2014 IEEE International Symposium on Inertial Sensors and Systems (ISISS), 2014: 1-4.

[10] Jeanroy A, Bouvet A, Remillieux G. HRG and marine applications [J]. Gyroscopy and Navigation, 2014, 5(2): 67-74.

[11] Rozelle D M. The hemispherical resonator gyro: From wineglass to the planets[C]. Proceedings of the 19thAAS/AIAA Space Flight Mechanics Meeting, 2009: 1157-1178.

[12] 方针, 余波, 彭慧,等. 半球谐振陀螺技术发展概述 [J]. 导航与控制, 2015, 14(3): 2-7.

[13] 齐轶楠, 赵辉, 赵万良,等. 半球谐振陀螺组合零偏稳定性提升技术研究 [J]. 导航定位与授时, 2015, 2(6): 63-68.

[14] Fan S C, Liu G Y, Wang Z J. On flexural vibration of hemispherical shell [J]. Applied Mathematics and Mechanics, 1991, 12(10): 1023-1030.

[15] Leland R P. Mechanical-thermal noise in MEMS gyroscopes [J]. IEEE Sensors Journal, 2005, 5(3): 493-500.

[16] Shang J T, Chen B Y, Lin W, et al. Preparation of wafer-level glass cavities by a low-cost chemical foaming process (CFP) [J]. Lab Chip, 2011, 11(8): 1532-1540.

[17] Shang J T. Foaming process for preparing wafer-level glass micro-cavities: U.S. Patent 8887527[P]. 2014-11-08.

[18] Luo B, Shang J, Zhang Y. Hemipherical wineglass shells fabricated by a chemical foaming process[C]. 16thInternational Conference on Electronic Packaging Technology (ICEPT), 2015: 951-954.

[19] 尚金堂, 罗斌. 微玻璃半球谐振陀螺及其圆片级制备方法: 中国, 201510963681.6[P]. 2016-05-04.

[20] 陈雪, 任顺清, 赵洪波,等. 半球谐振子薄壁厚度不均匀性对陀螺精度的影响 [J]. 空间控制技术与应用, 2009, 35(3): 29-33.

[21] 赵洪波. 半球谐振陀螺仪误差机理分析与误差抑制方法研究 [D]. 哈尔滨工业大学, 2013.

[22] 任顺清, 赵洪波. 谐振子密度偏差引起的频率裂解的分析 [J]. 哈尔滨工业大学学报, 2012, 44(3): 13-16.

[23] Luo B, Zhang M A, Lu C, et al. Wafer-level fabrication of silicon-in-glass electrodes for electrostatic transduction[C]. 2016 IEEE 66thElectronic Components and Technology Conference (ECTC), 2016: 1278-1283.

Design, Fabrication and Characterization of Micro Glass Hemispherical Shell Resonator

LUO Bin, SHANG Jin-tang

(School of Electronic Science & Engineering, Southeast University, Nanjing 210096, China)

DARPA has recently exerted effort towards the miniaturization of three dimensional shell resonator gyro, especially high-performance hemispherical resonator gyro, to achieve inertial-grade micromachined vibratory gyro. This paper proposes a foaming process to fabricate micro shell resonator with its diameter smaller than 1cm. The foaming process utilizes the thermal decomposition of the foaming agents under high temperature to release gas, and hence pressure difference and surface tensions drive the viscous glass to form 3D axisymmetric shells. Results show that the fabricated shell has the center frequency ofn=2 wineglass mode resonant frequency at 11kHz and a frequency split of 72Hz between the two degenerate modes (a relative frequency mismatch of 0.65%) with their correspondingQ-factor of 970 and 1127, respectively. The foaming process may provide a low-cost way for controllably shaping high-performance micro shell resonators.

Shell resonator gyro; Hemispherical resonator gyro; Hemispherical shell resonator; Foaming process; Micro shell resonator

2016-11-21；

2016-12-13

国家自然科学基金(51675102,51275091)

罗斌(1991-),男,博士研究生,主要从事微壳体谐振器和复合型基板等方面的研究。 E-mail：luobin0317@seu.edu.cn

通迅作者：尚金堂(1977-),男,教授,博士生导师,主要从事微纳器件制造与封装研究。 E-mail：jshang@seu.edu.cn

10.19306/j.cnki.2095-8110.2017.02.014

V241.3

A

2095-8110(2017)02-0079-07