PLCL-SS型ICPT系统距离及频率分叉特性研究*

王 珂,李 俊,许正平

(南京工业大学电气工程与控制科学学院,南京 211816)

PLCL-SS型ICPT系统距离及频率分叉特性研究*

王 珂,李 俊*,许正平

(南京工业大学电气工程与控制科学学院,南京 211816)

分析了原边LCL、副边串联补偿型感应电能传输系统的工作特性,推导了系统传输功率和传输效率与传输距离之间的定量关系;补偿电路的加入使得ICPT系统成为一个高阶系统,极易导致系统谐振频率不唯一;因此,采用回路阻抗角法分析了系统的频率分叉特性,并给出了近似消除系统频率分叉的参数匹配条件;最后,设计系统相关参数并进行实验验证。

PLCL-SS;ICPT;距离特性;频率分叉;参数匹配

在无线电能传输系统的发射侧和接受侧均加入无功补偿电路以保证系统传输的高效性及降低发射侧供电端的电源容量。双侧补偿电路按补偿电容的连接方式可分为4种:串联-串联、串联-并联、并联-串联、并联-并联。本文采用LCL型补偿电路,通过合理的参数设计,该补偿电路可以保证发射线圈电流基本恒定且不受互感及负载变化的影响,从而保证了电能传输的可靠性和稳定性。在无线电能传输系统的发射侧和接收侧分别施加补偿电路,提高ICPT系统的传输功率和效率有着积极的意义。然而,补偿电路的加入使得ICPT系统成为一个高阶系统。当系统的某些参数设计不合理,即系统参数不匹配时,将可能导致ICPT系统的谐振频率不唯一,此时ICPT系统出现了频率分叉。为保证ICPT系统高效、稳定地运行应尽量避免系统频率分叉现象的发生。

在对传输距离有特定要求的应用场合,如电动汽车无线充电、移动机器人无线充电等[4-5],研究无线电能系统传输功率、效率与传输距离的定量关系就显得十分重要[6]。本文推导了ICPT系统传输功率、效率与传输距离的表达式;采用回路阻抗角法对系统的频率分叉特性进行研究[7-8],并给出近似消除系统频率分叉的参数匹配条件;建立了ICPT系统实验平台并进行了实验验证。

1 ICPT系统特性分析

本文以发射侧LCL谐振、接收侧LC串联谐振的无线电能传输系统为例进行分析,其拓扑结构如图1所示。

对图1进行简化可得其等效电路,如图2所示。其中,Ui为高频逆变后的输入电压基波有效值;Uo为二次侧交流输出电压值;Lp和Ls分别为系统发射线圈、接收线圈的电感;Cp和Cs分别为系统一次侧、二次侧的补偿电容;电感Li、电容Cp和发射线圈电感Lp构成一次侧LCL谐振网络;接收线圈电感Ls和电容Cs构成二次侧串联谐振网络;Rac为负载电阻;M为发射、接收线圈间的互感;电能正是通过发射侧和接收侧的互感完成非接触传输的。

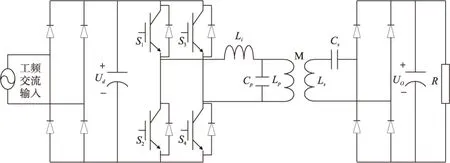
图1 ICPT系统拓扑图

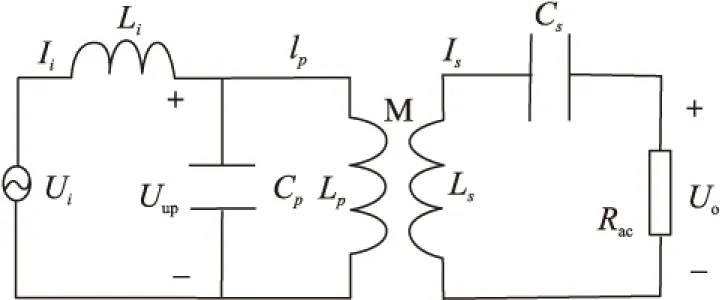
图2 LCL型系统等效电路图

由电路完全谐振的特点可知,全桥逆变输出的交流方波电压可只考虑其基波分量,即为图2中Ui。它与其直流侧输入电压Udc之间的关系表示为式(1):

(1)

为简化推导过程,现定义系统固有谐振频率ω0、工作频率归一化频率ωn、LCL补偿电路的电感比例系数α分别为式(2)和式(3)所示:

(2)

(3)

现假定系统始终处于完全谐振状态,即LCL型无线电能传输的工作频率等于其固有谐振频率。那么,LCL型系统交流输入阻抗Zin可表示为

(4)

式中:等效阻抗Req为发射线圈电感内阻Rp和接收侧折算至发射侧的反映阻抗之和,忽略接收线圈电感内阻,则Req可表示为

(5)

将式(2)、式(3)、式(5)代入式(4),可得LCL型无线电能传输系统交流输入阻抗简化形式,如式(6)所示:

(6)

由式(6)可知,当电感比例系数α等于1时,LCL型无线电能传输系统交流输入阻抗呈纯阻性,实现了输入单位功率因数。此时,LCL型无线电能传输系统交流输入阻抗可表示为式(7):

(7)

根据式(7),推导可得LCL型补偿电路输入电流Ii、发射线圈电感电流Ip,分别表示为式(8)和式(9):

(8)

(9)

结合式(9),可得LCL型无线电能传输系统接收侧输出电压Uo和输出电流Is,分别表示为式(10)和式(11):

(10)

(11)

现定义系统传输效率η为输出功率Po与输入功率Pi的比值,根据式(5)、式(7)、式(8)、式(10)和式(11)可得LCL型无线电能传输系统的输入功率Pi、输出功率Po及传输效率η,分别表示为式(12)～式(14):

(12)

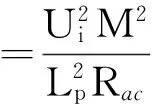
(13)

(14)

2 系统传输功率、传输效率与传输距离的关系

依据文献[3]可知,当系统发射线圈和接收线圈采用螺旋绕制方式且发射和接收线圈同轴摆放时,ICPT系统的传输距离与发射接收线圈的互感关系可表示为式(15):

(15)

式中:μ0为真空磁导率;np和ns分别表示系统发射和接收线圈的匝数;rp和rs分别表示系统发射和接收线圈的半径;d表示系统传输距离。

将式(15)代入式(13)、式(14)中可得ICPT系统传输功率、传输效率与传输距离的关系,分别表示为式(16)和式(17):

(16)

(17)

3 频率分叉特性

如图2所示,以发射侧LCL谐振补偿和接收侧串联电容补偿的感应电能传输系统为例,对发射侧回路阻抗角进行分析并推导其表达式。根据式(3)、式(4)并令式(3)等于1可得ICPT系统发射侧回路阻抗,如式(18)所示:

(18)

进一步简化可得,发射侧回路阻抗的实部和虚部分别表示为式(19)、式(20):

(19)

(20)

式中:A的表达式见于式(21):

(21)

因此,发射侧回路阻抗角可表示为式(22):

(22)

将式(2)、式(18)、式(19)代入式(22)可将发射侧回路阻抗角表示为式(23):

(23)

式中:k表示发射侧和接收侧线圈的耦合系数,Qs表示接收侧回路的品质因数;k和Qs分别表示为式(24)、式(25)。

(24)

(25)

根据前面的分析可知,PLCL-SS补偿型ICPT系统发射侧回路阻抗角的大小受系统归一化工作频率ωn、发射侧和接收侧线圈的耦合系数k和接收侧回路的品质因数Qs的约束。下面将分析ωn、k、Qs和发射侧回路阻抗角的关系。

(1)给定Qs时,ωn、k与发射侧回路阻抗角的关系

依次给定Qs为5、10、20,依据式(23)可以得出它们的变化关系图,见于图3。

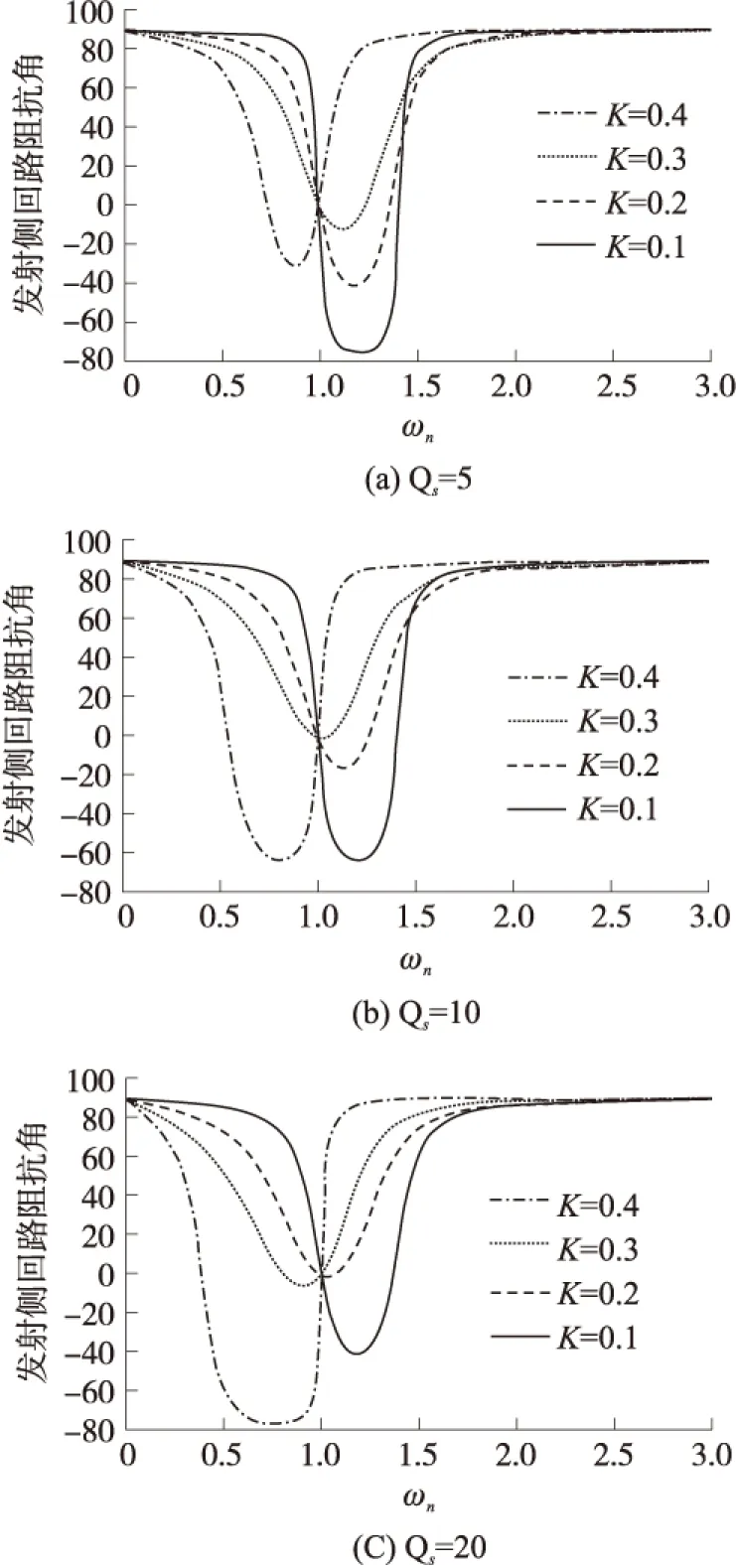
图3 发射侧回路阻抗角与k的关系

(2)给定k时,ωn、Qs与发射侧回路阻抗角的关系

依次给定k为0.1、0.2、0.3,依据式(23)可以得出它们的变化关系图,见于图4。

图4 发射侧回路阻抗角与Qs的关系

分析图3可得,随着接收侧回路的品质因数Qs的增加,近似满足消除ICPT系统频率分叉的耦合系数k将减小;分析图4可得,随着耦合系数k的增加,近似满足消除ICPT系统频率分叉的接收侧回路的品质因数Qs将减小。

经过以上分析得出了发射侧回路阻抗角与耦合系数k、接收侧回路的品质因数Qs、归一化工作频率ωn之间的变化关系。下面将对PLCL-SS补偿型ICPT系统的频率分叉特性进行理论推导。

(26)

由式(26)化简可得

(27)

频率分叉现象的发生表明式(3-31)存在除ωn=1之外的其他解,即存在ωn≠1使得式(3-33)成立。

(28)

求取式(28)的根判别式,如式(29):

(29)

由于式(29)大于0恒成立,即式(28)有解。因此,式(26)存在多个解,即系统发生了频率分叉现象。

求出式(28)的解(负值已舍去)并表示为

(30)

为了保证ICPT系统高效运行,应使得式(30)的取值接近1,从而近似达到避免ICPT系统的频率分叉现象的目标。现设定式(30)的取值为0.99,求解可得耦合系数k、接收侧回路的品质因数Qs应满足式(31):

(31)

4 实验验证

为了进一步研究ICPT系统的工作特性,本文建立了原边LCL、副边串联补偿的感应电能传输系统实验平台,如图5所示。

图5 LCL型无线电能传输系统实验平台

根据上述分析设计了相关参数,系统实验平台各参数值如表1中所示。其中,Lx、Cx构成LC滤波环节,串联接入LCL补偿网络与高频逆变环节之间,以改善输入电流波形。

表1 样机参数

在不同传输距离条件下进行了实验,对不同传输距离下的传输功率和传输效率进行了定量分析,依据实验结果及理论值绘制了样机传输功率和传输效率与传输距离的关系曲线图,如图6和图7所示。

图6 传输功率曲线

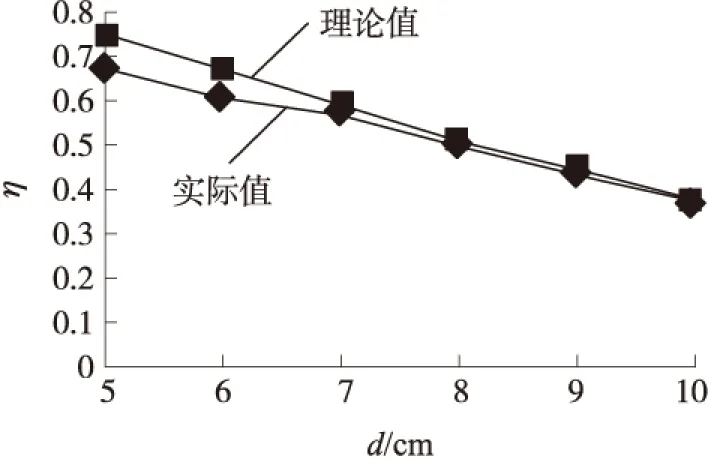
图7 传输效率曲线

5 结论

本文研究了原边LCL、副边串联补偿型感应电能传输系统的工作特性,推导了系统传输功率和效率与传输距离之间的定量关系;由于补偿电路的加入使得ICPT系统成为一个高阶系统,极易导致系统谐振频率不唯一,因此,本文采用回路阻抗角法分析系统的频率分叉特性,并给出了近似消除系统频率分叉的参数匹配条件;根据理论分析设计系统相关参数并搭建了ICPT系统实验平台;在不同的传输距离条件下进行了实验,实验结果与理论值基本符合。综上,本文对ICPT系统参数设计具有一定的参考价值。

[1] Fotopoulou K,Flynn B W. Wireless Power Transferin Loosely Coupled Links:Coil Misalignment Model[J]. IEEE Transactions on Magnetics,2011,47(2):416-430.

[2] Villa J L,Sallan J,Sanz Osorio J F,et al. High-Misalignmenttolerant Compensation Topology for ICPT Systems[J]. IEEE Transactions on Industrial Electronics,2012,59(2):945-951.

[3] 傅文珍,张波,丘东元,等. 自谐振线圈耦合式无线电能传输的最大效率分析与设计[J]. 中国电机工程学报,2009,29(18):21-26.

[4] 孙跃,夏晨阳,戴欣,等. 感应耦合电能传输系统互感耦合参数的分析与优化[J]. 中国电机工程学报,2010,30(33):44-50.

[5] 周雯琪,马皓,何湘宁. 感应耦合电能传输系统不同补偿拓扑的研究[J]. 电工技术学报,2009,24(1):133-139.

[6] 陈文仙,陈乾宏,张惠娟. 电磁共振式无线电能传输系统距离特性的分析[J]. 电力系统自动化,2015,39(8):98-104.

[7] 孙跃,吴静,王智慧,等. ICPT系统基于电容阵列的稳频控制策略[J]. 电子科技大学学报,2014,43(1):54-59.

[8] 邹爱龙,王慧贞,华洁. 基于LCL补偿的多负载移动式感应非接触电能传输系统[J]. 中国电机工程学报,2014,24:4000-4006.

Research on the Distance and Frequency Bifurcation Characteristics of ICPT Type PLCL-SS System*

WANGKe,LIJun*,XUZhengping

(College of Electrical Engineering and Control Science,Nanjing Technology University,Nanjing 211816,China)

Operating characteristics of inductive power transmission system in PLCL-SS compensation type was analyzed,and the quantitative relationship between the system transmission power and transmission efficiency and transmission distance were derived;Compensation circuits make ICPT(Inductively Coupled Power Transfer)system become a high-order system,easily making system resonant frequency not only;So the loop impedance angle method was used to analysis the system frequency bifurcation characteristics,and the parameter matching conditions of eliminating the system frequency bifurcation was given;Finally,design of the system parameters and the experimental verification were done.

PLCL-SS;ICPT;distance characteristic;frequency bifurcation;parameter matching

项目来源:国家自然科学基金项目(50977086)

2016-04-07 修改日期:2016-06-05

C:7310G;7320C

10.3969/j.issn.1005-9490.2017.02.023

TM131.41

A

1005-9490(2017)02-0375-05