一种MEMS扭摆式强磁场测量传感器*

徐雪祥,张 鉴,鲍 霖,戚昊琛,杨文华

(合肥工业大学电子科学与应用物理学院,合肥 230009)

一种MEMS扭摆式强磁场测量传感器*

徐雪祥,张 鉴,鲍 霖,戚昊琛*,杨文华

(合肥工业大学电子科学与应用物理学院,合肥 230009)

提出了一种扭摆式结构的MEMS电容式强磁场传感器,采用洛伦兹力驱动,通过测量硅板扭摆导致的电容变化来检测外部磁场强度,测量磁场的量程设计在0.2 T～2 T之间。首先介绍了传感器的工作原理,然后对其进行仿真,分析其物理特性,建立了模型并且求解出各阶模态下的振动形式,得到传感器主振模态频率为28.26 kHz。并模拟了受力过程中的形变量。最后介绍了其制造工艺流程,验证了传感器加工的可行性。

MEMS;磁场传感器;洛伦兹力;扭摆式

磁场传感器与人们的生活息息相关,广泛应用于汽车工业、消费电子、导航仪表、军事工业等方面。随着微电子机械系统(MEMS)的发展,磁场传感器趋于小型化、高集成度,使得制造成本大大降低[1-4]。MEMS磁场传感器具有小尺寸、低成本以及性能独特的优点,具有强大的竞争力和发展前景[5-6]。近年来,出现了多种MEMS磁场传感器,如Salvatore Baglio等人提出的基于洛伦兹力的MEMS磁场传感器,这种传感器基于悬臂梁结构,由于外加磁场和已知电流相互作用,使得悬臂梁受到洛伦兹力而变形,再通过硅应力计来测量该形变。Sunier R[9-10]提出了一种新的谐振式磁场传感器,利用频率的改变作为信号的输出,实现磁场的测量。Thieny C和Leichl C等人提出了梳齿状磁场传感器,利用永磁体和外磁场相互作用,使梳齿产生扭矩,从而测得磁场方向。陈洁等人提出了U型梁结构的磁场传感器,具有结构简单、测试方便、分辨率高的特点。大部分已提出的磁场传感器,都不适合强磁场的测量。

本文基于扭摆式原理,提出了一种新的强磁场检测MEMS传感器结构,采用电容检测方式,具有量程大、结构简单、分辨率高、功耗低等特点。该扭摆式传感器结构可适用于核磁共振仪,磁压力金属工件加工装置,磁约束受控热核聚变装置等对强磁场有特殊测量要求的领域。

1 传感器结构设计与工作原理

提出的磁场传感器结构如图1所示,传感器主要由一块方形硅板构成,尺寸为1 mm×1 mm,厚度100 μm。硅板由100 μm长,30 μm宽的扭转梁支撑。硅板上表面淀积一层二氧化硅绝缘层,厚500 nm。二氧化硅上层为金属线圈和感应电极,金属线圈由一端外沿锚区接入,环绕在硅板外层,从中心锚区引出。当交变电流通过线圈时,线圈在外磁场中受到洛伦兹力

F=IL×B

(1)

式中:I为电流强度大小,L为硅板长度,B为传感器所处磁场中磁场强度大小。洛伦兹力开始带动硅板摆动,磁力矩大小由式(2)给出:

T=IS×B

(2)

式中:S是方向垂直于线圈平面的矢量,大小等于线圈面积。

图1 磁场传感器原理图

硅板开始摆动后,线圈切割磁感线而产生感应电动势,大小为

ξ=BLv

(3)

式中:v为金属线圈振动速度。为了提高传感器灵敏度,应使其在谐振频率处振动。当所加的电流频率与结构本征频率相同时,传感器发生谐振,此时振幅最大。硅板摆动的振幅大小与外部磁场强度B成正比,摆动幅度由镶嵌于硅板内侧的感应电极检测得出。由于硅板绕转轴摆动,使得硅板上感应电极与衬底上感应电极的间距发生变化,从而改变了电容大小。通过检测电容的改变量,即可测出硅板摆动幅度。

该磁场传感器可由带阻尼的谐振子模型表示。转动惯量I与转轴的弹性系数有关。运动中的阻尼主要来自周围的气体,阻尼大小由阻尼系数γ确定。运动方程可表示为

(4)

式中:T是作用在谐振板上的外力矩,κ是转轴的弹性系数,θ为硅板相对于转轴的偏转角。用谐振子的机械品质因数来表示每个振荡周期能量损耗与储能之间的关系,由式(5)给出

Q=(ω0I)/γ

(5)

式中:ω0是谐振角频率

(6)

偏转角可由方程(3)解得,结果如式(7)所示:

(7)

振幅和的相位与相对频率的关系如图2所示,静电激励用来抵消系统的阻尼。当激励频率等于谐振子的机械频率,即ω/ω0=1时,振幅随着品质因数Q的增加而增加当外力矩以正弦方式变化时,角位移可表示为:

(8)

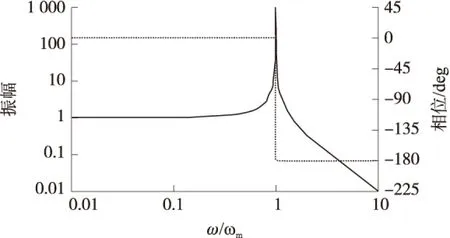
图2 振幅、相位与相对频率ω/ω0的关系

2 传感器的特性分析

2.1 模态分析

模态是结构系统的固有振动特性,线性系统的自由振动被解耦合为N个正交的单自由度振动系统,对应系统的N个模态。

为验证所提出磁场传感器结构的可行性,使用ANSYS进行了有限元仿真。通过结构动力学仿真得到了磁场传感器的各阶模态,从而可得出磁场传感器的频率响应特性。同时,通过结构静力分析得出磁场传感器在使用过程中扭转梁的形变量,为器件的加工尺度提供参考。表1为有限元仿真时使用的相关参数。

表1 有限元仿真的相关参数

传感器的前8阶模态如图3所示。

图3 传感器结构的前八阶模态

根据仿真结果,可得1阶～8阶模态的共振频率分别为:28.26 kHz,153.10 kHz,168.88 kHz,227.10 kHz,353.72 kHz,354.34 kHz,529.55 kHz,576.86 kHz。

由于在主振模态下振动幅度最大,为了提高传感器的灵敏度,防止其他振动模态对灵敏度的影响,采用其主振模态下工作,即一阶模态。硅板外围金属线圈受到洛伦兹力产生周期性运动,其频率与所通交流电频率一致。由于其摆动振幅大小影响了硅板感应电极与衬底电极间电容值的大小,当电流激励频率与固有机械振荡频率达到谐振时,振动相干加强,此时更易于测量电容值的改变量,从而更易于确定外部磁场强度。

2.2 品质因数分析

品质因数是反映阻尼振动系统能量衰减情况的重要物理量,品质因数的确定对于系统运动状态的分析十分关键。在本文所提出的磁场传感器结构中,品质因数可表示为:

(9)

式中:β为振幅放大因子,ζ为阻尼比。系统的阻尼主要来源于两个方面:结构阻尼和粘滞阻尼。常温常压下,结构阻尼比气体阻尼小得多,可忽略不计。粘滞阻尼主要是由于空气流动的阻力。由于传感器微结构尺寸小,其表面积与体积之比较大,因此挤压空气膜产生的空气阻尼效应变得十分显著。

空气阻尼的作用可用雷诺方程来描述:

(10)

式中:P为空气薄膜上的压力,ρ为空气密度,μ为空气的粘滞系数,h是空气膜的厚度,x、y为平面的坐标。

由于传感器尺寸较小,温度变化的影响很小,恒温条件下,气体密度ρ和压力P成正比,雷诺方程可改写为:

(11)

本文所提出的扭摆结构传感器原理图如图4所示。

图4 扭摆式传感器结构原理图

分子与平板挤压产生的能量为:

(12)

式中:l为间隙的横向位移,vyz0和vx0分别为分子进入间隙时y-x平面和x方向的速度分量。

由此得到一次振动的能量损失为:

(13)

近似计算得到:

(14)

由定义得到品质因数为:

(15)

ρP是平板的密度。

由此可计算出品质因数Q的值约为1 000。

2.3 应力分析

在磁场传感器工作过程中,扭转梁受到扭转力而发生形变,考虑到机械强度的要求,为了使其不至于因形变而断裂,扭转梁长度与宽度必须满足一定的条件。同时也要考虑灵敏度的要求,改变扭转梁的长度与宽度会对灵敏度造成影响。

在磁场强度为1T的磁场中,通过136μA的交变电流,金属线圈所受洛伦兹力约为1.36×10-9N·μm。通过有限元仿真,在传感器边缘金属导线处施加外力得到传感器的应力云图如图5所示。

根据仿真所得应力结果,经过反复分析计算,采用100μm长,30μm宽的扭转梁能够使保证传感器的使用寿命,且能保证一定的灵敏度。

图6 传感器剖视图

3 传感器的制备工艺流程

传感器由单独加工的单晶硅圆片键合而成。底部圆片与包含可动结构的中部圆片使用直接键合工艺相接触。在加工完金属线圈,并利用深反应离子刻蚀释放可动硅板后,将二氧化硅顶盖阳极键合到单晶硅圆片上。传感器剖视图如图6所示。

传感器制备的工艺流程如图7所示。

(a)选取两片纯净的单晶硅片;(b)淀积一层氧化层,并刻蚀形成空腔;(c)将上层硅片加工成可动硅板,淀积一层氧化层,镀上金属线圈与电极,完成扭转梁;(d)使用有硅贯穿的硼硅玻璃加工顶盖,镀铝膜作为电极,并将金属钛膜片加工在顶盖底部来保证空腔为真空;(e)将加工好的二氧化硅顶盖与底部空腔阳极键合。

图7 传感器的制备工艺流程

4 结论

本文提出了一种基于扭摆式结构的MEMS强磁场传感器,设计了高强度的扭转梁结构,并使用电容检测方式测定外部磁场场强。通过阻尼振动模型推导出传感器结构的品质因数,并用ANSYS软件对传感器的不同模态振动方式及受力形变进行了模拟。仿真实验表明该传感器可用于强磁场的测量。传感器结构简单,体积小,成本低,制造采用MEMS加工工艺,易于大批量生产,可用于特定场合的磁场测量。

[1] 宋海宾,杨平,徐立波. MEMS传感器随机误差分析及处理[J]. 传感技术学报,2013,26(12):1719-1723.

[2] 郭兴军,李朋伟,张文栋,等. 基于电容式MEMS器件的静电斥力驱动研究[J]. 仪器仪表学报,2014,35(8):1738-1743.

[3] Zhu J X,Jie Lin,Nuh Sadi Yuksek,et al. Dynamic Phenomena and Analysis of MEMS Capacitive Power Harvester Subjected to Low-Frequency Excitations[J]. Nonlinear Dynamics,2015,79(1):673-688.

[4] 贺婷,杨杰,孔龄婕,等. MEMS压电-磁电复合式振动驱动微能源的设计[J]. 传感技术学报,2015,28(3):342-346.

[5] 刘诗斌,陈露兰,张韦,等. 一种基于磁传感器的MEMS陀螺标定方法[J]. 传感技术学报,2013,26(12):1700-1703.

[6] 田武刚,胡佳飞,潘孟春,等. MEMS磁力线聚集和垂动调制磁场传感器[J]. 国防科技大学学报,2014,36(4):129-133.

[7] Brugger S,Paul O. Geometric Optimization and Microstructuring of Magnetic Concentrators for a Resonant Magnetic Sensor[C]//International Conference on Solid. State Sensors,Actuators and Microsystems. France:Transducers,2007:2377-2380.

[8] Brugger S,Paul O. Resonant Magnetic Microsensor with gT Resolution[C]//Proceedings of the IEEE 21st Annual International Conference on Micro Electro Mechanical Systems. USA:Tucson,2008:944-947.

[9] Sunier R,Li Y. Resonant Magnetic Field Sensor with Frequency Output[C]//18th IEEE International Conference on Micro Electro Mechanical Systems. Miami,2005:339-342.

[10] Sunier R,Vancura T,Kirstein K U,et al. Resonantmagnetic Field Sensor with Frequency Output[J]. Journal of Icroelectromechanical Systems,2006,15(5):1098-1107.

[11] Leichle T C,Arx M V,Allen M G. Amicromachined Resonant Magnetic Field Sensor[C]//The 13th IEEE Micro Electro Mechanical Systems. Switzerland:Interlaken,2001:274-277.

[12] Leichle T C,Arx M V,Reiman S,et al. A Low-Power Resonant Micromachinedcompass[J]. Journal of Micromechanics and Microengineering. 2004,14(4):462-470.

[13] 陈洁,秦明,黄庆安. MEMS磁场传感器的设计及测试[J]. 东南大学学报(自然科学版),2011,41(5):929-933.

[14] 陈洁,黄庆安,秦明. MEMS磁场传感器的研究进展[J]. 电子器件,2006,29(4):1384-1388.

A Novel MEMS Magnetic Field Sensor with a Torsional Pendulum Structure*

XUXuexiang,ZHANGJian,BAOLin,QIHaochen*,YANGWenhua

(School of Electronic Science and Applied Physics,Hefei University of Technology,Hefei 230009,China)

A novel MEMS magnetic field sensor based on a torsional pendulum structure is presented. The amplitude of the vibration,which is proportional to the magnetic field,is detected by sensing capacitors. The measuring range of the sensor is designed to vary from 0.2 T to 2 T. The excitation of the resonator is achieved by the Lorentz force generated by a sinusoidal current flowing through a metal coil,which is deposited on the surface of the structure. The resonance frequencies and modes of the resonators are simulated by the general purpose finite element program,with the frequency of the first mode being 28.26 kHz. Furthermore,the manufacture process of the sensor is proposed to illustrate the feasibility of the device.

MEMS;magnetic field sensor;Lorentz force;torsional pendulum structure

项目来源:国家自然科学基金项目(61404042);合肥工业大学实验室自制仪器设备项目(Z201518);省级大学生创新训练项目(2016CXCYS091)

2016-03-27 修改日期:2016-04-14

C:5100;7230

10.3969/j.issn.1005-9490.2017.02.008

TP212

A

1005-9490(2017)02-0301-05