GNSS信号数据/导频扩频码配对优化方法

段召亮，秦丽娴，韩明明，杨再秀，杨文津

(1.卫星导航系统与装备技术国家重点实验室，河北 石家庄 050081； 2.中国人民解放军61773部队，新疆 乌鲁木齐 830000)

GNSS信号数据/导频扩频码配对优化方法

段召亮1，秦丽娴1，韩明明2，杨再秀1，杨文津1

(1.卫星导航系统与装备技术国家重点实验室，河北 石家庄 050081； 2.中国人民解放军61773部队，新疆 乌鲁木齐 830000)

为了提高载波相位跟踪的稳健性和伪码跟踪精度，现代全球卫星导航系统(Global Navigation Satellite System，GNSS)普遍采用数据/导频并存的信号结构。针对数据/导频信号的互相关性影响码跟踪性能的问题，提出了一种数据/导频扩频码配对优化方法。优化准则是：在一定的超前减滞后间距条件下，单独跟踪导频信号时通道内互相关干扰导致的码跟踪平均误差最小。以全球定位系统(Global Positioning System，GPS)L1C频点信号为例，基于接口控制文件(Interface Control Document，ICD)给出的扩频码族，进行了数据/导频扩频码的配对优化设计，并仿真对比了不同配对方案的码跟踪性能。分析结果表明，优化后的配对方案能有效削弱数据/导频通道内的互相关干扰，提高导航信号的码跟踪性能。

数据/导频；扩频码；互相关；码跟踪；GPS L1C

0 引言

伪随机码[1](或扩频码)不仅是接收机区分不同卫星信号的依据，也是区分同一信号不同分量(如数据和导频)的依据。特别是对于数据和导频通道中的伪随机码，由于它们同时(即码相位一致)、同相(即载波相位相同)的特点，其互相关性的大小将直接影响GNSS接收机的跟踪性能[2]。

随着GPS现代化[3]和Galileo系统建设的推进，伪码设计方面的研究工作也取得了很大进展。为改善信号性能，Galileo E1 OS引入了全新的Random码。与传统的伪随机码不同，Random码不能通过移位寄存器生成[4]。同时，GPS L1C也选用新的伪码序列，即基于勒让德序列的Weil码[5]。Weil码和Random码的出现与新伪码判据的提出有关，如平衡性、零自相关旁瓣特性和奇/偶相关性等[6]。GPS L1C和Galileo E1 OS的伪随机码在设计阶段主要考虑码本身的特性(如奇/偶相关性等)，对于具体的调制方式、复用方式和数据/导频共存等特点考虑较少。理论上讲，Random码和Weil码仅在数据和导频信号采用正交调制时才是最佳的[7]。但实际上，无论是Galileo E1 OS，还是GPS L1C，它们的数据和导频信号都是同相发射的。因此，有必要研究数据/导频信号互相关性对导航信号性能的影响及优化方法。2008年，S Wallner对比了Galileo E1 OS伪码的自、互相关性，并分析了其对信号捕获性能的影响。2010年，D Margaria等基于干扰误差包络[8]，分析了GPS L1C、Galileo E1 OS的数据/导频互相关性对抗干扰性能的影响[9]。显然，他们都没有考虑数据和导频之间的互相关性对跟踪性能的影响，这将会直接影响导航用户的测距精度与定位精度。

针对这一问题，本文从数据/导频信号基带跟踪性能出发，通过分析导航信号数据/导频互相关性[10]对接收性能带来的影响，提出了一种基于导频信号扩频码重新分配的优化配对方法，并通过仿真分析证明了该方法形成的扩频码配对结果在数据/导频独立通道跟踪方面较原始配对方案的优越性，为数据/导频复合信号的扩频码族优化设计提供参考。

1 数据/导频信号

GPS L1C将采用BOC调制[11]方式，信号包括2个通道，即无数据的导频通道和调制电文的数据通道。GPS L1C的数据通道采用BOC(1,1)调制，导频信号选用TMBOC(6,1,4/33)调制。TMBOC(6,1,4/33)时分复用BOC(1,1)和BOC(6,1)分量，其中包括29/33的BOC(1,1)和4/33的BOC(6,1)时隙[12]。

L1C的扩频码选用基于勒让德序列的Weil码，周期为10 ms，码速率为1.023 MHz。L1C的扩频码族包括210个数据/导频扩频码对。另外，为改善信号的性能，其导频信号增加了二次编码(码片宽度是10 ms，码长为1 800)。在后面的讨论中主要关注最坏的情况下数据/导频互相关干扰对码跟踪误差的影响。所谓最坏的情况，就是假设处理过程中数据和导频信号的相对符号关系是不变的。此时，可忽略二次编码和电文的影响。

2 数据/导频互相关性导致的码跟踪误差

考虑到电文的随机性，要实现数据/导频复合信号的匹配跟踪是比较困难的，因此主要考虑单独跟踪数据或导频通道的情况。导频信号无电文调制，故相干积分时间不受电文宽度限制，一般来说接收机仅对导频信号进行跟踪。考虑到L1C的数据和导频是同相发射的(即调制载波相位相同)，单独跟踪导频信号时，本地信号与输入信号之间不是自相关，而是数据和导频的复合信号与导频信号之间的互相关。众所周知，自相关函数是偶函数，而互相关函数却未必如此，这可能会引起码鉴相曲线(即S-曲线)的畸变，从而导致码跟踪误差。同样，仅跟踪L1C数据信号(可降低接收机复杂度)时也会有类似的问题。下面通过S-曲线偏移，分析数据/导频互相关性对码跟踪性能的影响。

接收机码鉴相曲线过零点的码相位延迟，即为S-曲线偏移。对于连续超前滞后(Coherent Early-late Processing，CELP)鉴相器来说，S-曲线可表示为[13]：

Sc(ε,Δ)=Rx/y(ε+Δ/2)-Rx/y(ε-Δ/2)。

(1)

对应的过零点(即锁定点)εbias(Δ)定义为：

Sc(εbias(Δ),Δ)=0。

(2)

式中，Rx/y(τ)为x(t)和y(t)的互相关函数；Δ为超前减滞后间距；ε为码延迟；εbias(Δ)为鉴相曲线(S-曲线)偏移。这里，x(t)代表L1C信号(即数据/导频复合信号)，y(t)仅代表数据或导频信号。

GPS L1C的S-曲线及局部放大效果如图1所示，其中，卫星号为22，鉴相器类型为CELP，Δ=1码片，分析条件为前端带宽无限大，且忽略数据通道信息跳变带来的影响。图1中分别给出了L1C匹配跟踪、只跟踪导频信号L1C/TMBOC以及只跟踪数据信号即L1C/BOC(1,1)这3种情况下的S-曲线。由于互相关函数的非对称性，L1C/TMBOC和L1C/BOC(1,1)分别带来了1.73 m和-3.84 m的S-曲线偏移。这就是由数据/导频的互相关性引起的码跟踪误差。它们会直接影响测距精度，最终导致用户的定位精度下降。

单独跟踪GPS L1C的导频或数据通道时的码跟踪误差(即S-曲线偏移)如图2所示，分析条件与图1相同。由于PRN64～210的扩频码序列是预留给其他GNSS系统和星基增强系统的，因此图2中仅考虑了GPS空间段使用的PRN1～63。由图2可见，不同卫星信号的码跟踪误差并不相同。因此，通道内互相关干扰的影响在定位解算时是不能忽略的。

图1 GPS L1C伪码鉴相曲线及局部放大

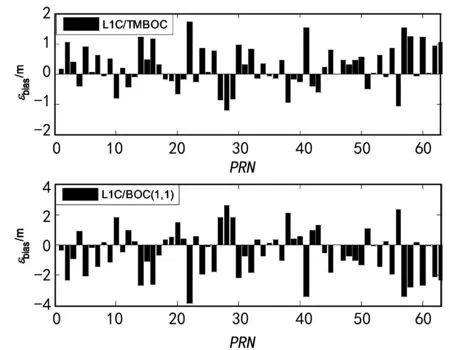
图2 通道内互相关性导致的码跟踪误差

为更好地反映数据/导频互相关性对码跟踪性能的整体影响，定义平均S-曲线偏移为：

(3)

式中，N为信号数量。对于GPS L1 PRN1～63来说，N=63。

单独跟踪GPS L1C的导频和数据通道时的码跟踪平均误差如图3所示，分析条件与图2相同。虽然导频通道(即TMBOC)的功率较高，但是其抗互相关干扰的能力受超前减滞后间距的影响却较大。由于调制方式的差异，L1C/TMBOC的最大平均误差出现在超前减滞后间距为0.3码片附近，而L1C/BOC(1,1)则出现在间距为1码片处。另外，当超前减滞后间距小于0.9码片时，L1C/BOC(1,1)的平均误差与超前减滞后间距变化近似成线性关系。

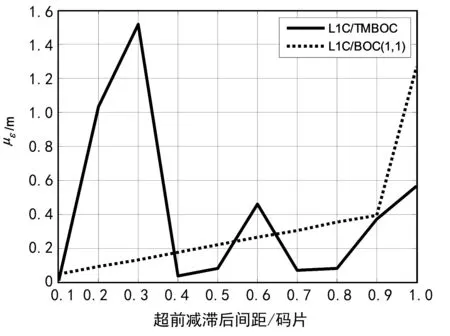
图3 通道内互相关性导致的码跟踪平均误差

3 数据/导频扩频码配对优化

单独跟踪L1C的数据或导频信号时，通道内(即数据/导频)互相关干扰会导致码跟踪误差。为了减小通道内互相关干扰，本文考虑对现有的GPS L1C数据/导频扩频码进行配对优化。不改变ICD中数据和导频扩频码原有的分组情况，仅对导频通道的扩频码进行重新分配，从而形成新的数据/导频扩频码配对关系。

导频信号的引入主要是为了提高GNSS信号的跟踪性能。因此，本文提出的配对优化评价准则是：一定超前减滞后间距条件下，单独跟踪导频信号时(即L1C/TMBOC)的码跟踪平均误差最小。其中，优化参考间距为0.3码片。由图3可知，单独跟踪导频信号条件下，GPS L1C在超前减滞后间距为0.3码片时出现最大码跟踪平均误差。

考虑GPS L1C的63个数据/导频扩频码对，分别定义数据和导频扩频码族：

(4)

为了得到优化的数据/导频扩频码配对关系，需要计算所有可能的扩频码对下，单独跟踪导频信号(即L1C/TMBOC)时的S-曲线偏移。定义误差矩阵：

BN×N= bias(ad,ap)=

(5)

显然，该优化问题最直观的解法就是枚举法。但是，由于N值较大，枚举法的运算量过大，不宜采用。实际上，这里的配对优化可看作是“运筹学”中的经典问题——指派问题(Assignment Problem)。该配对优化问题可采用“匈牙利”算法求解[14]，求解过程如下：

① 找出误差矩阵|BN×N|每一行中的最小元素。在最小元素所在的行，从每个元素中减去该最小元素，构建一个新的矩阵。对于这个新的矩阵，找出每一列中的最小元素。在最小元素所在的列，从每个元素中减去该最小元素，构建一个新的矩阵(称为缩减误差矩阵)。

② 画出数量最少的直线(水平、垂直或二者)，使得它们能够覆盖缩减误差矩阵中的所有零。如果需要N条直线，那么在矩阵的被覆盖的零当中就能够求出最优解；如果需要的直线少于N条，则转入③。

③ 在缩减误差矩阵中，找出没有被②中所画直线覆盖的最小非零元素(它的值记为ζ)。现在从缩减误差矩阵的每个未覆盖元素中减去ζ，给被2条直线覆盖的元素加上ζ。然后返回②。

优化后的数据/导频扩频码配对关系如表1所示。其中，“PRN/数据”行给出的是GPS L1C ICD中的PRN和数据扩频码编号。“导频”行给出的是GPS L1C ICD中的导频扩频码编号。该扩频码与其上一行同列的扩频码组成新的扩频码对。例如，优化后PRN1的数据/导频扩频码对为(1,63)，其中，“1”代表ICD中数据扩频码序列编号，而“63”代表ICD中导频扩频码序列编号。

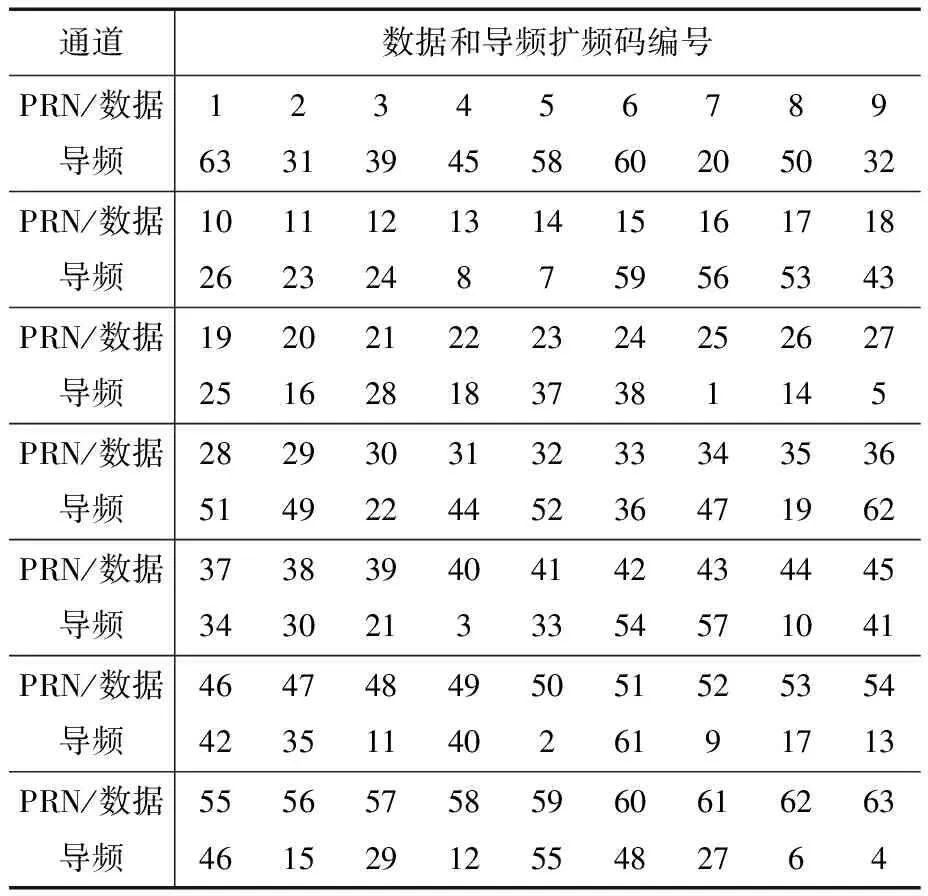
表1 优化后的GPS L1C数据/导频扩频码配对关系

4 仿真结果分析

经优化配对后，通过接收算法模拟平台[15]对码跟踪误差进行仿真分析。单独跟踪数据或导频信号时，优化前后的码跟踪平均误差对比如图4所示(分析条件与图3相同)。

图4 优化前后码跟踪平均误差对比

经过优化后，数据导频支路码跟踪精度均得到明显提升。与未优化情况相比，当超前减滞后间距在[0.1,1]码片范围内时，L1C/TMBOC和L1C/BOC(1,1)的码跟踪平均误差均显著减少。优化后L1C/TMBOC的最大误差出现在0.2码片附近。

经过优化后的码跟踪平均误差增益如图5所示。优化性能增益受超前减滞后间距的影响较大。最大增益约为14 dB，而最小增益仅为5 dB左右。L1C/TMBOC的最大增益(约14 dB)同时出现在0.3码片和0.4码片附近。对于L1C/BOC(1,1)来说，最大增益(约14 dB)则出现在0.3码片、0.6码片和0.9码片附近。除了超前减滞后间距为0.1码片和0.4码片的情况外，L1C/TMBOC和L1C/BOC(1,1)的优化增益比较接近。该结论可为相关信号类型接收机设计[16]过程中的环路策略选择提供一定参考依据。

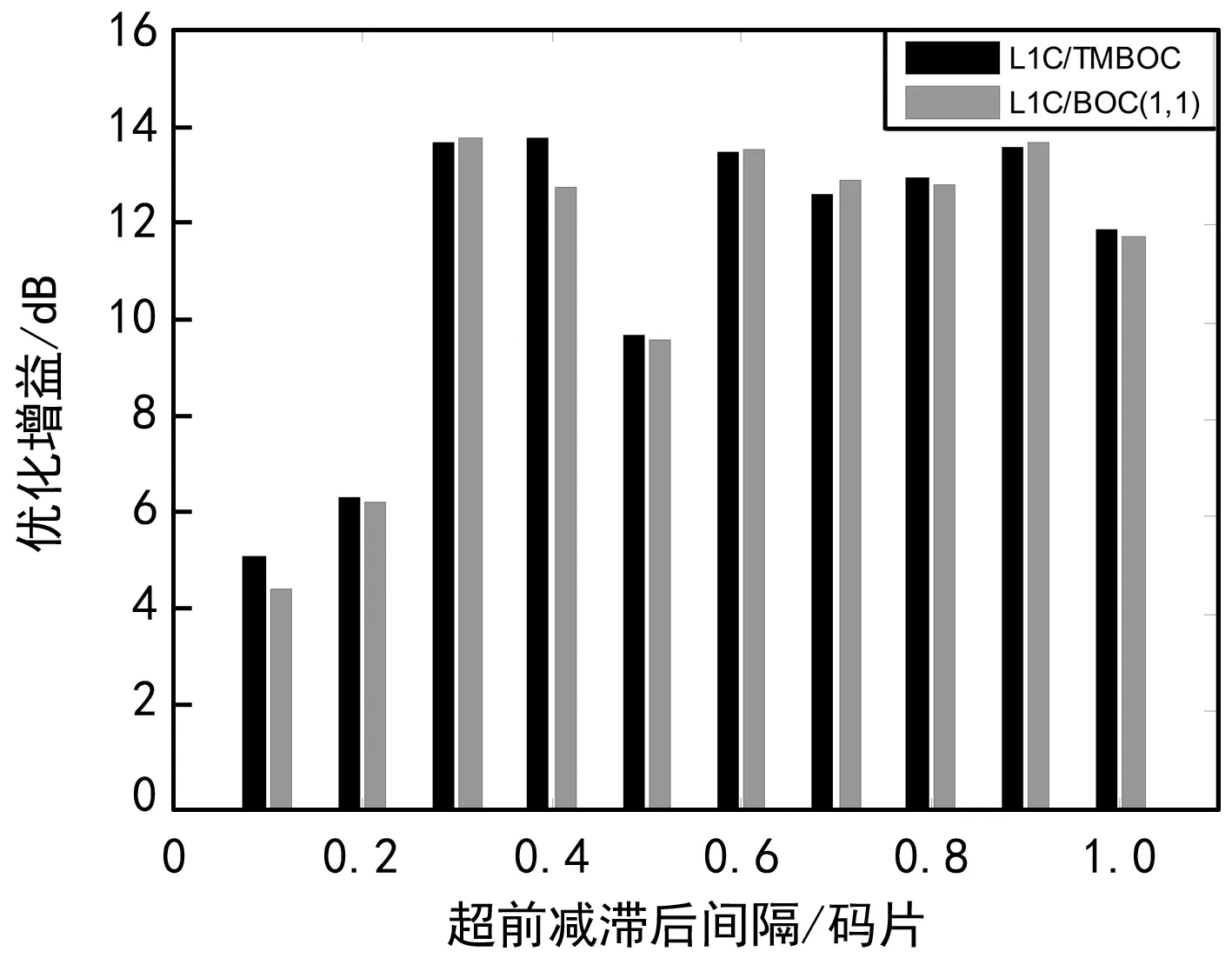
图5 码跟踪性能优化增益

5 结束语

单独跟踪数据或导频信号时，通道内互相关干扰会导致码跟踪误差。另外，不恰当的超前减滞后间距会导致接收处理性能进一步恶化。基于ICD的扩频码族，本文给出了GPS L1C的数据/导频扩频码优化配对方案。与未优化结果相比，优化方案能有效地减小通道内互相关干扰，提高码跟踪性能，为以数据导频模式为基础的航信号体制设计提供重要的参考依据。由于未改变原来的扩频码族，因此优化方案对通道间和系统间(如GPS和Galileo)的互相关性不会产生不利影响。本文的研究表明，数据和导频信号的互相关性应成为扩频码设计和优化过程中的一个重要参考指标。同时，考虑到扩频码设计的复杂性，建议数据/导频复合信号的设计过程分为2个阶段。首先，仅考虑码自身的特点(如奇/偶相关性，0、1平衡性等)，设计出整个扩频码族。然后，利用本文提出的分析模型及优化方法，综合考虑扩频码和信号调制的特点，进一步优化设计。

[1] 谢 钢.GPS原理与接收机设计[M].北京：电子工业出版社，2012.

[2] HEIN G W,AVILA-RODRIGUEZ J A,Wallner S.The DaVinci Galileo Code and Others[J].Inside GNSS,2006,1(6):62-74

[3] 黄智伟.GPS接收机电路设计[M].北京：国防工业出版社，2006.

[4] 何成龙，王 垚.GPS L1C信号Weil码相关性能分析[J].无线电通信技术，2013，39(1)：32-35.

[5] RUSHANAN J J.The Spreading and Overlay Codes for the L1C Signal[J].Navigation,2007,54(1):43-51.

[6] RUSHANAN J J.Weil Sequences:a Family of Binary Sequences with Good Correlation Properties[C]∥ IEEE International Symposium on Information Theory,Seattle,WA,2006:1 648-1 652.

[7] WALLNER S,AVILA-RODRIGUEZ J A,HEIN G W.Galileo E1 OS and GPS L1C Pseudo Random Noise Codes-Requirements,Generation,Optimization and Comparison[C]∥ Proceedings of ION GNSS 2007,Fort Worth,TX,2007:1 549-1 563.

[8] WALLNER S,AVILA-RODRIGUEZ J A,WON J H,et al.Revised PRN Code Structures for Galileo E1 OS[C]∥ Proceedings of ION GNSS 2008,Savannah,GA,2008:887-899

[9] MOTELLA B,SAVASTA S,MARGARIA D,et al.Method for Assessing the Interference Impact on GNSS Receivers[J].IEEE Transactions on Aerospace and Electronic Systems,2011,47(2):1 416-1 432.

[10] 杨再秀.GNSS信号性能评估关键技术研究[D].北京：北京航空航天大学，2013.

[11] 袁润平，翟建勇，王 伟.卫星导航系统中的BOC调制和接收技术分析[J].现代导航，2013(4)：252-257.

[12] MARGARIA D,SAVASTA S,DOVIS F,et al.Codes Cross-correlation Impact on the Interference Vulnerability of Galileo E1 OS and GPS L1C signals[C]∥ Proceedings of ION ITM 2010,San Diego,CA,2010:941-951.

[13] HEIN G W,AVILA-RODRIGUEZ J A,WALLNER S,et al.MBOC:the New Optimized Spreading Modulation Recommended for Galileo L1 OS and GPS L1C[J].Inside GNSS,2006,1(4):57-65.

[14] SOELLNER M,KURZHALS C,HECHENBLAIKNER G,et al.GNSS Offline Signal Quality Assessment[C]∥ Proceedings of ION GNSS 2008,Savannah,GA,2008:909-920.

[15] 管吉兴，陈 荣，高跃清，等.一种扩频接收机的设计分析[J].无线电通信技术，2011，37(5)：58-61.

[16] 马英昌，谢 松.GPS L5接收机的设计与实现[J].无线电通信技术，2013，39(6)：94-96.

段召亮 男，(1979—)，高级工程师。主要研究方向：卫星导航、GNSS基带信号处理。

秦丽娴 女，(1989—)，助理工程师。主要研究方向：卫星导航、导航终端技术。

Data/Pilot PRN Code Pairs Optimization Method for GNSS Signals

DUAN Zhao-liang1,QIN Li-xian1,HAN Ming-ming2,YANG Zai-xiu1,YANG Wen-jin1

(1.StateKeyLaboratoryofSatelliteNavigationSystemandEquipmentTechnology,ShijiazhuangHebei050081,China; 2.Unit61773,PLA,UrumuchiXinjiang830000,China)

In order to increase the robustness of the carrier tracking loop and improve the resistance of the code tracking loop to thermal noise,modern Global Navigation Satellite Systems(GNSS) introduce the pilot channel in addition to the navigation data channel.In view of the impact of data/pilot cross-correlation on code tracking performance for satellite navigation system signals,a novel method to optimize data/pilot Pseudo Random Noise(PRN) code pairs is presented.The optimization goal is to obtain the minimum average code tracking error when only the pilot components are tracked for specific early-late spacing.Based on the code set given by the Interface Control Document(ICD),the optimized data/pilot PRN code pairs for the Global Positioning System(GPS) L1C signal are provided.The code tracking performance of un-optimized and optimized signals is analyzed and compared by software simulations.Analyses show that the optimization method could significantly mitigate the interference of data/pilot intra-channel cross-correlation,and then improve the code tracking performance of navigation signals.

data/pilot;pseudo random noise code;cross-correlation;code tracking;GPS L1C

10.3969/j.issn.1003-3106.2017.05.15

段召亮,秦丽娴,韩明明,等.GNSS信号数据/导频扩频码配对优化方法[J].无线电工程,2017,47(5):62-66.[DUAN Zhaoliang,QIN Lixian,HAN Mingming,et al.Data/pilot PRN Code Pairs Optimization Method for GNSS Signals[J].Radio Engineering,2017,47(5):62-66.]

2017-02-06

国家高技术研究发展计划(“863”计划)基金资助项目(2012AA121802)。

TN967.1

A

1003-3106(2017)05-0062-05