大运动曲梁应力刚化效应特征值分析

张建书　芮筱亭　顾俊杰

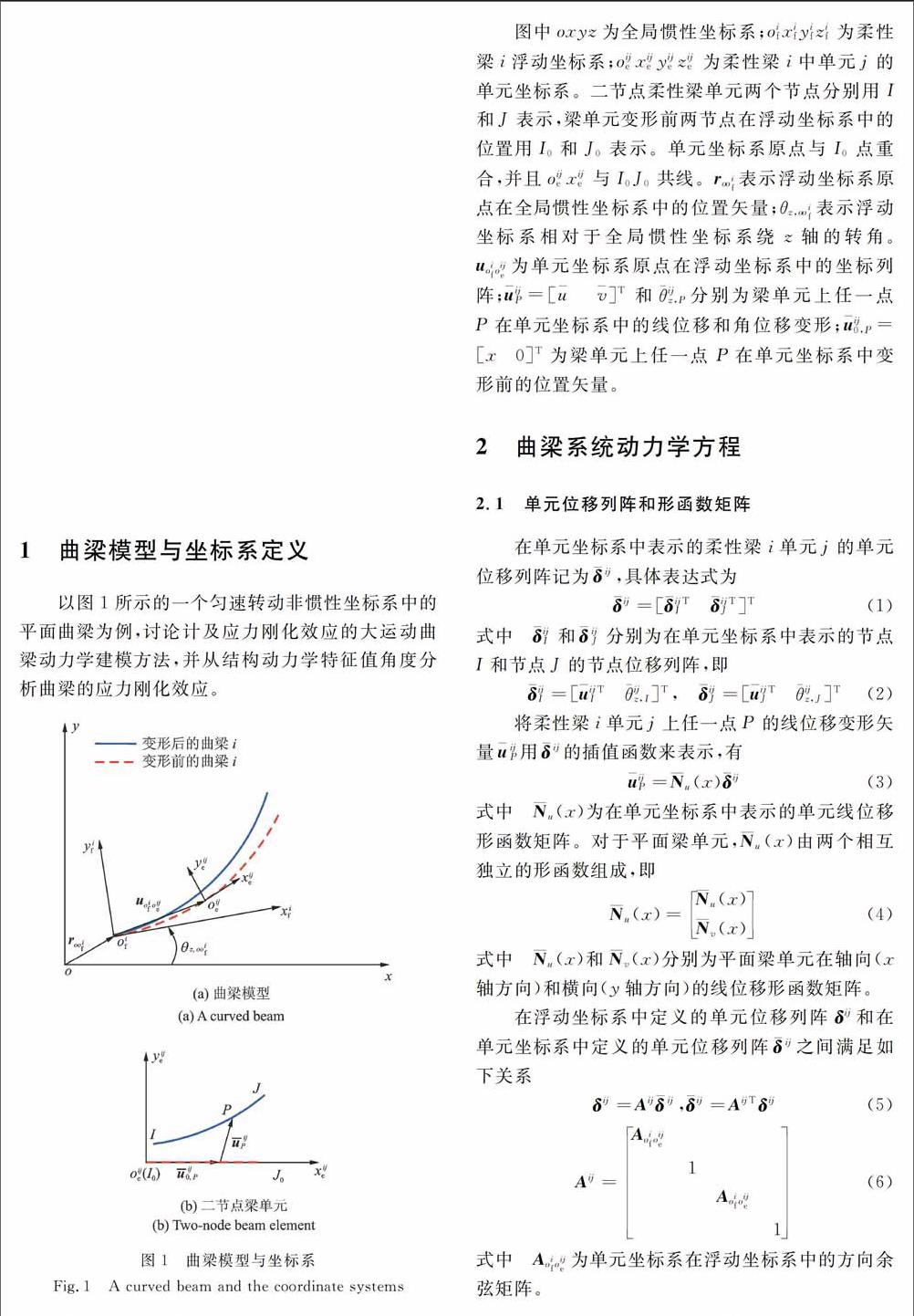
摘要：从连续介质力学非线性位移一应变关系出发，导出计人应力刚化效应的柔性梁变形能表达式。利用哈密顿变分原理和浮动框架有限元方法（Finite Element Method of Floating Frame of Reference，简记为FEMFFR）导出了匀速转动非惯性系中曲梁的动力学方程。通过数值仿真分析了曲梁的旋转软化（Spin Softening）和应力刚化（Stress Stiffening）效应，并与ANSYS软件仿真结果进行了对比，从结构动力学特征值角度验证了基于连续介质力学非线性位移一應变关系为高速旋转曲梁引入应力刚化效应的方法的正确性。由于曲梁结构不再像直梁结构那样拥有独立的纵向和横向振动模态，为此讨论了改进的Craig-Bampton模态综合法在一般运动曲梁系统中的应用及其缩减策略，为利用浮动框架有限元方法建立满足基于小变形假设的高速旋转柔性曲梁动力学模型提供了参考。

关键词：多体系统动力学；曲梁；浮动框架有限元法；应力刚化；模态综合法

引言

从描述柔性体的位移和变形的策略这一角度可以将当前较为流行的柔性多体系统动力学方法分为两大类：相对节点坐标描述方法和绝对节点坐标描述方法。相对节点坐标法也称为浮动框架法或混合坐标法，该方法用描述柔性构件大范围运动浮动框架的刚体坐标与描述柔性体相对于浮动框架的位置和变形坐标来描述柔性体在全局惯性系中的运动。该方法较为直观并有众多模态降阶方法，对大运动小变形柔性多体系统尤为适合。绝对节点坐标法中单元节点坐标定义在全局坐标系下，并采用斜率矢量代替传统有限元方法中的节点转角坐标，能精确描述大运动大变形柔性多体系统。

利用浮动坐标方法对满足小变形假设的大运动柔性多体系统进行动力学计算时，如果忽略柔性梁纵向变形与横向变形的耦合作用，由于离心惯性力的作用，使得柔性体元件的等效刚度随着浮动框架转速提高而降低。不计人柔性梁纵向变形与横向变形耦合作用的计算结果与实验结果是相背的。

文献在前期研究的基础上提出了上述问题的一种解决方法：通过引入横向变形引起的纵向缩短效应这一几何非线性因素导出大运动柔性梁的一次耦合模型。文献研究了柔性梁的一次耦合模型的模态降阶方法，并与有限元方法的结果进行了对比。文献研究了做空间任意运动柔性梁的动力学方程，同时考虑了横向弯曲对纵向变形的影响。文献比较了零次模型、一次耦合模型及精确模型的差异，探讨了各种模型的适用性。由于在一次耦合模型中，需要通过沿着梁的轴线方向对整个柔性梁进行积分以获取横向弯曲变形引起的梁的轴向缩短效应，所以将该方法推广到具有一般初始构形的曲梁结构具有一定的难度。

文献根据非线性连续介质力学理论，从非线性位移一应变关系出发，通过对纵向和横向变形节点坐标进行坐标分离，解出与纵向变形相关的准静态方程，得到准静态时的纵向应力表达式，从而获得附加刚度项。仿真结果与一次耦合模型吻合较好。该方法避免了一次耦合模型建模方法中关于浮动坐标系方向连续积分的因素，但是对纵向和横向变形采用了独立的模态阵型，所以需要对该方法进行改进才能将其推广应用到具有一般初始构形的曲梁结构。

文献讨论了曲梁的动力学建模方法，但均未计入应力刚化效应对曲梁动力学的影响，因此不适用于高速大运动曲梁的动力学仿真。计人应力刚化效应的大运动曲梁的动力学模型在文献中尚很少见。

本文从连续介质力学非线性位移一应变关系出发，讨论将应力刚化效应引入到大运动曲梁动力学模型的方法。首先从弹性体非线性位移一应变关系出发导出计人应力刚化效应的柔性梁变形能表达式；再利用哈密顿变分原理和浮动框架有限元法，建立具有一般初始构形柔性曲梁在匀速转动非惯性系中的动力学方程；然后从结构动力学特征值角度分析大运动曲梁的应力刚化效应。由于曲梁不再像直梁那样拥有独立的纵向振动模态和横向振动模态，同时为了使曲梁的振动模态满足各种连接约束条件，因此最后一节讨论改进的Craig-Bampton模态综合法在一般运动曲梁系统动力学中的应用及其缩减策略，为利用浮动框架有限元方法建立满足基于小变形假设的高速旋转柔性曲梁动力学模型提供参考。