非均匀节点情形下的一类三角B样条曲线
谢宇迪,蒋新昕
(辽宁师范大学 数学学院 ,辽宁 大连116029)
非均匀节点情形下的一类三角B样条曲线
谢宇迪,蒋新昕
(辽宁师范大学 数学学院 ,辽宁 大连116029)
给出一类在非均匀节点情形下带参数的三角B样条基函数,讨论了这类基函数的性质以及在重节点情形时的变化,并利用这类基函数构造了相应的三角B样条曲线,这类曲线具有与二次非均匀B样条曲线相似的性质。在控制顶点不变的情况下,可以通过改变形状参数取值来调节曲线的形状。此外,它还能精确表示圆、椭圆等曲线。
非均匀B样条;基函数;曲线设计
0 引言
三角样条曲线在计算机辅助几何设计中被广泛地应用[1],SCHOENBERG I J[2]首次提出三角样条的概念, 韩旭里教授在三角样条函数的研究中,提出并讨论了分段的二次三角多项式曲线、三次三角多项式曲线及带有参数的二次三角多项式曲线[3-5]的性质和应用 ;文献[6]提出了k(k≥2)阶的带形状参数三角多项式均匀B样条曲线,可以精确表示圆、椭圆等一些曲线;文献[7]提出了带多形状参数的非均匀三角多项式曲线,它是同类型单形状参数曲线的推广。
本文给出了另一类基于四点分段的带参数非均匀二次三角B样条曲线,当所有节点等距时,此类曲线即成为文献[8]中的均匀二阶三角B样条曲线,对于给定控制点,利用参数的不同取值可以局部或整体地控制曲线形状,而无须通过改变控制点调整曲线的形状,此外,还给出了该曲线表示椭圆和圆的方法。通过实例表明,所给曲线具有结构简单、使用灵活的优点,为曲线设计提供了一种有效的方法。
1 带形状参数二阶三角B样条基函数
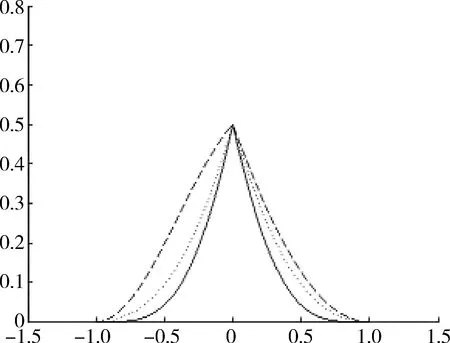
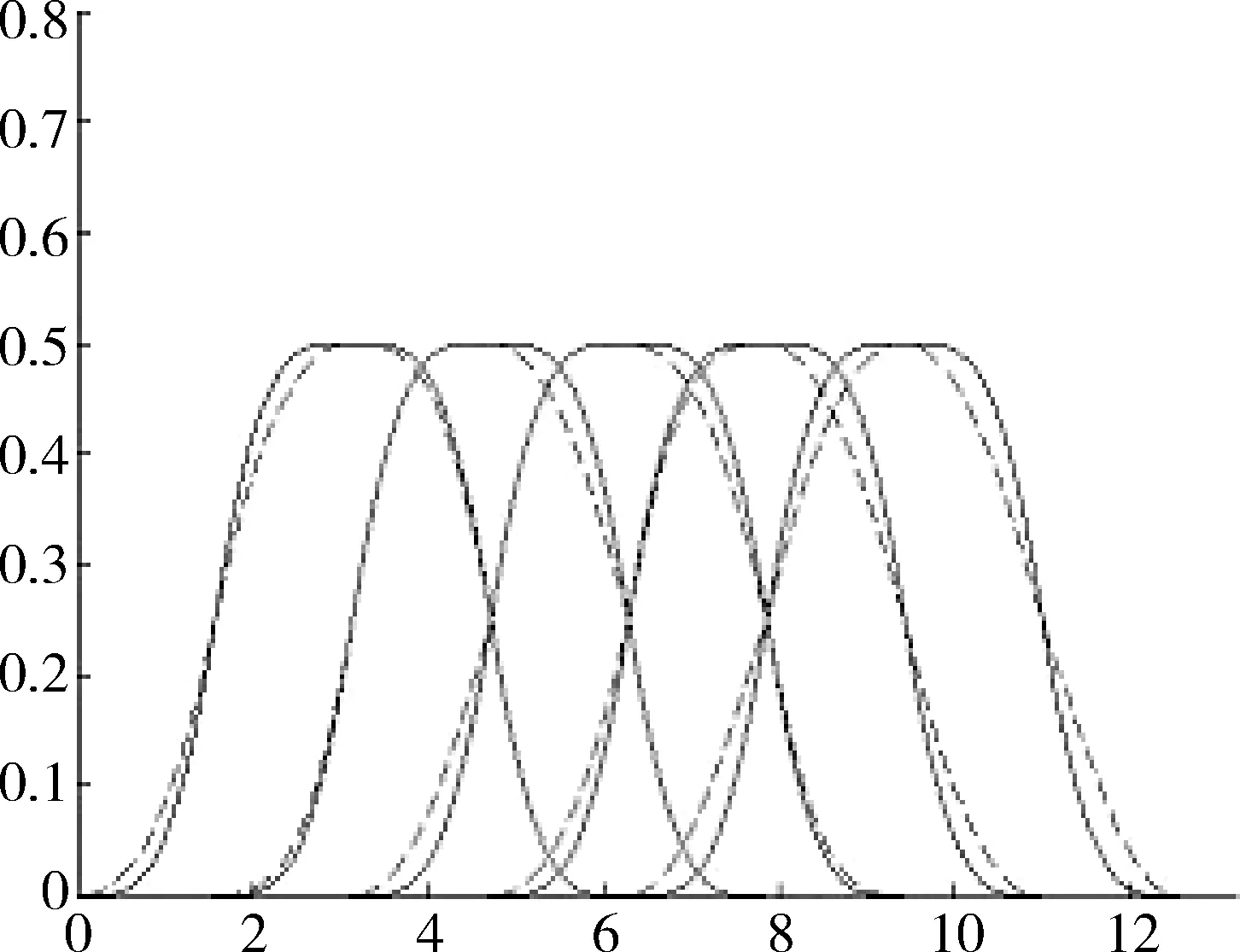
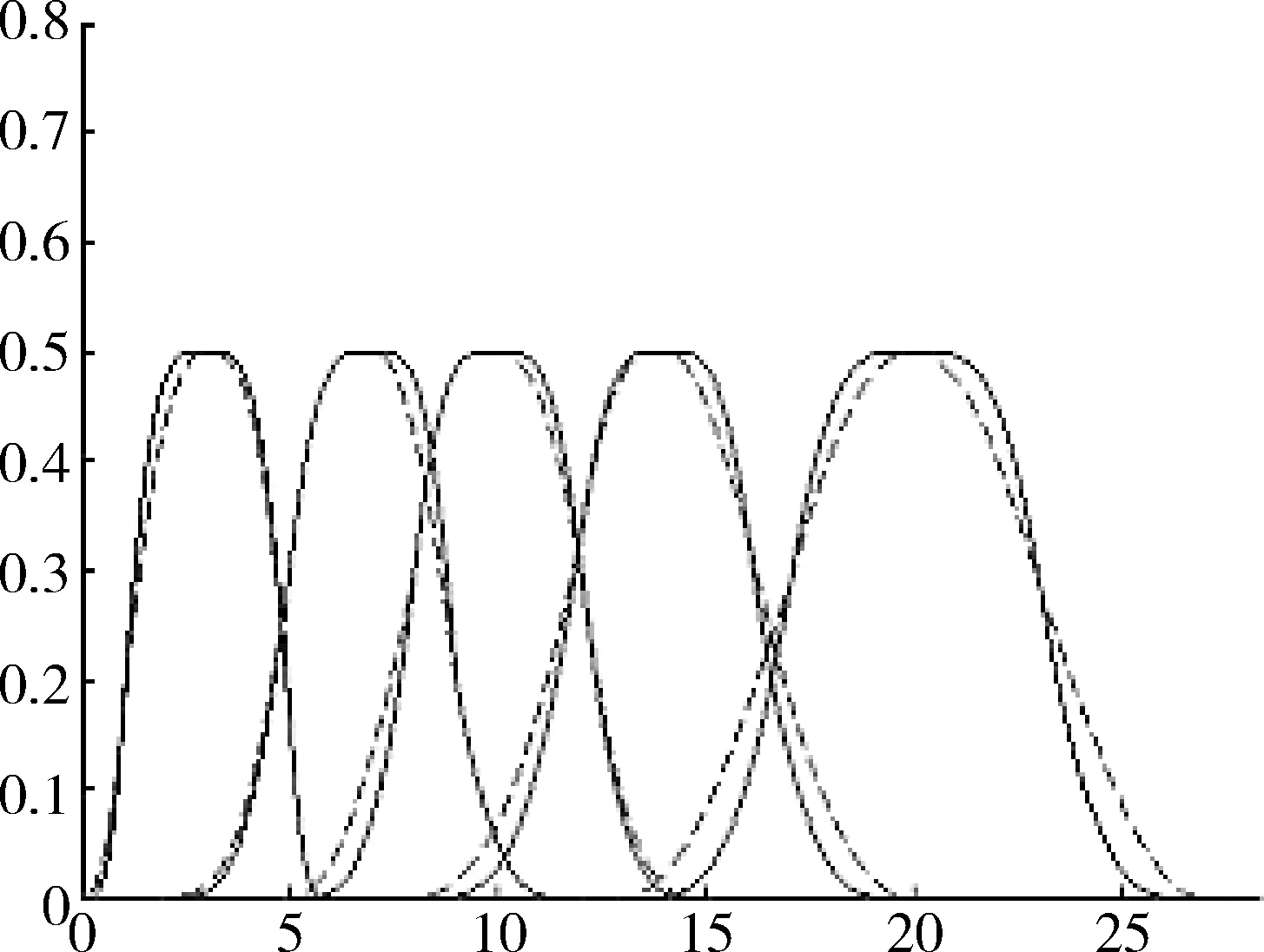
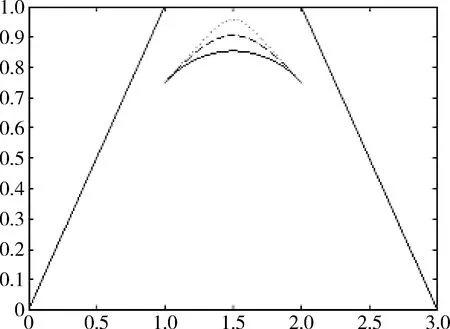
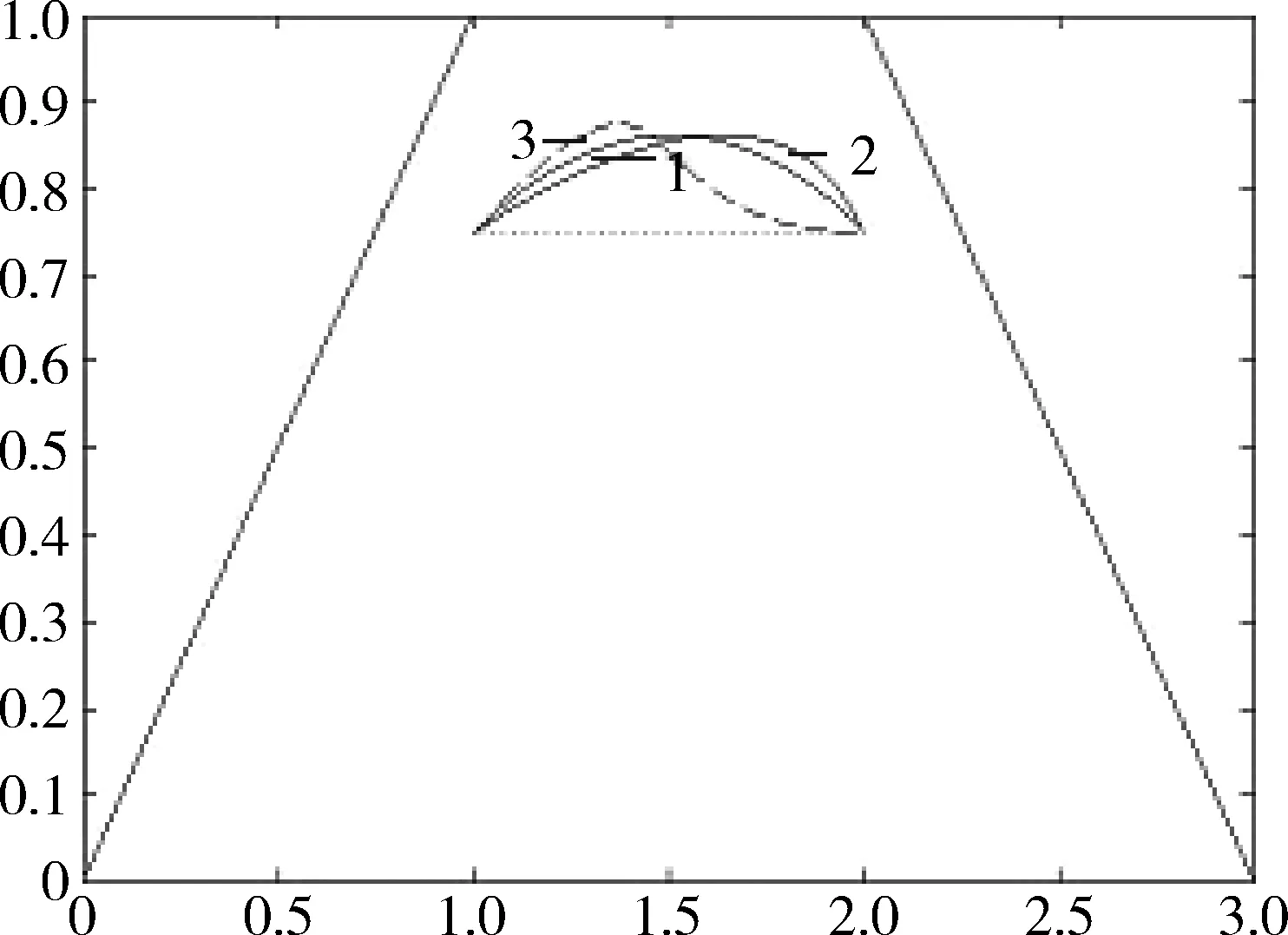
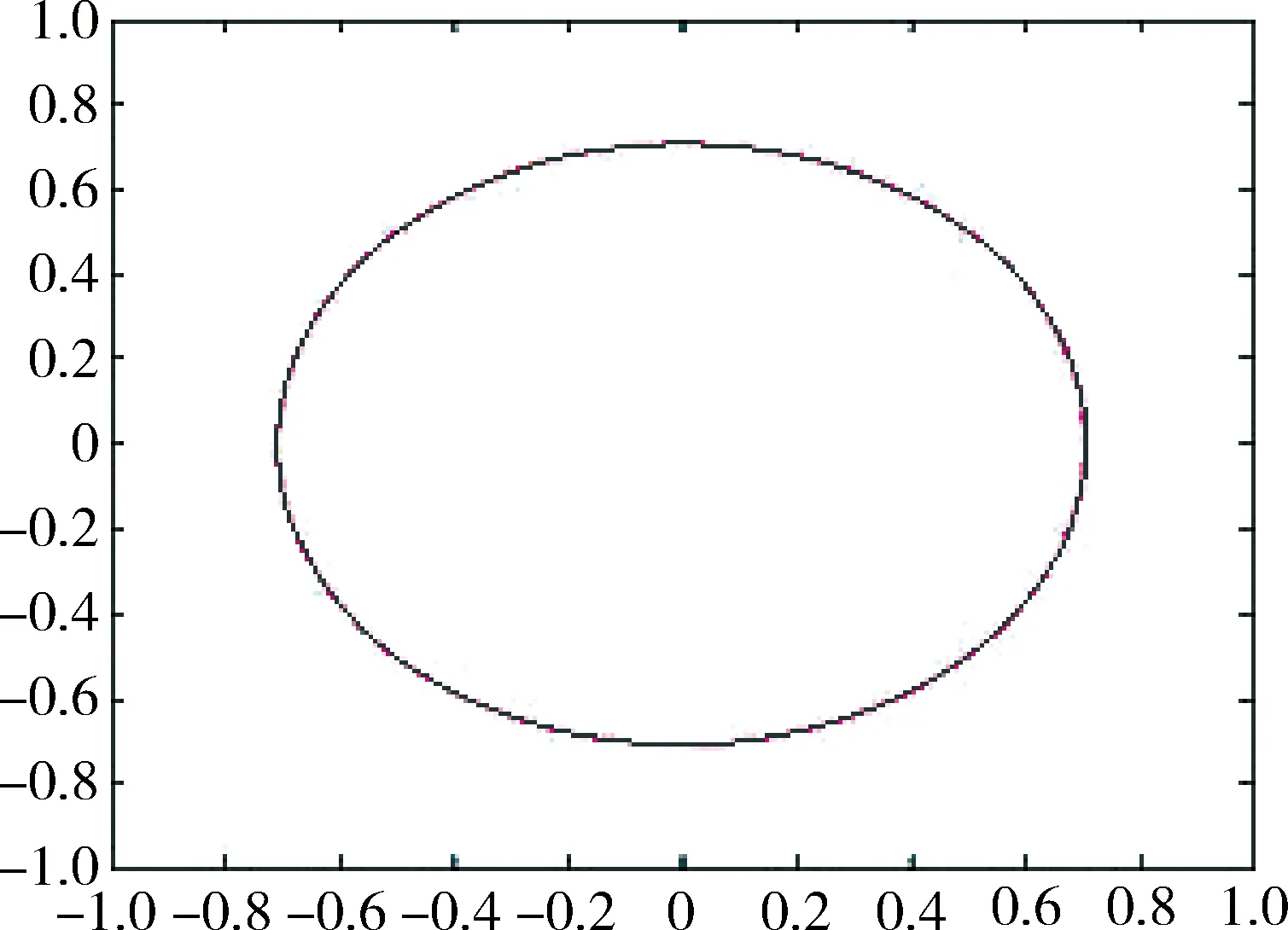
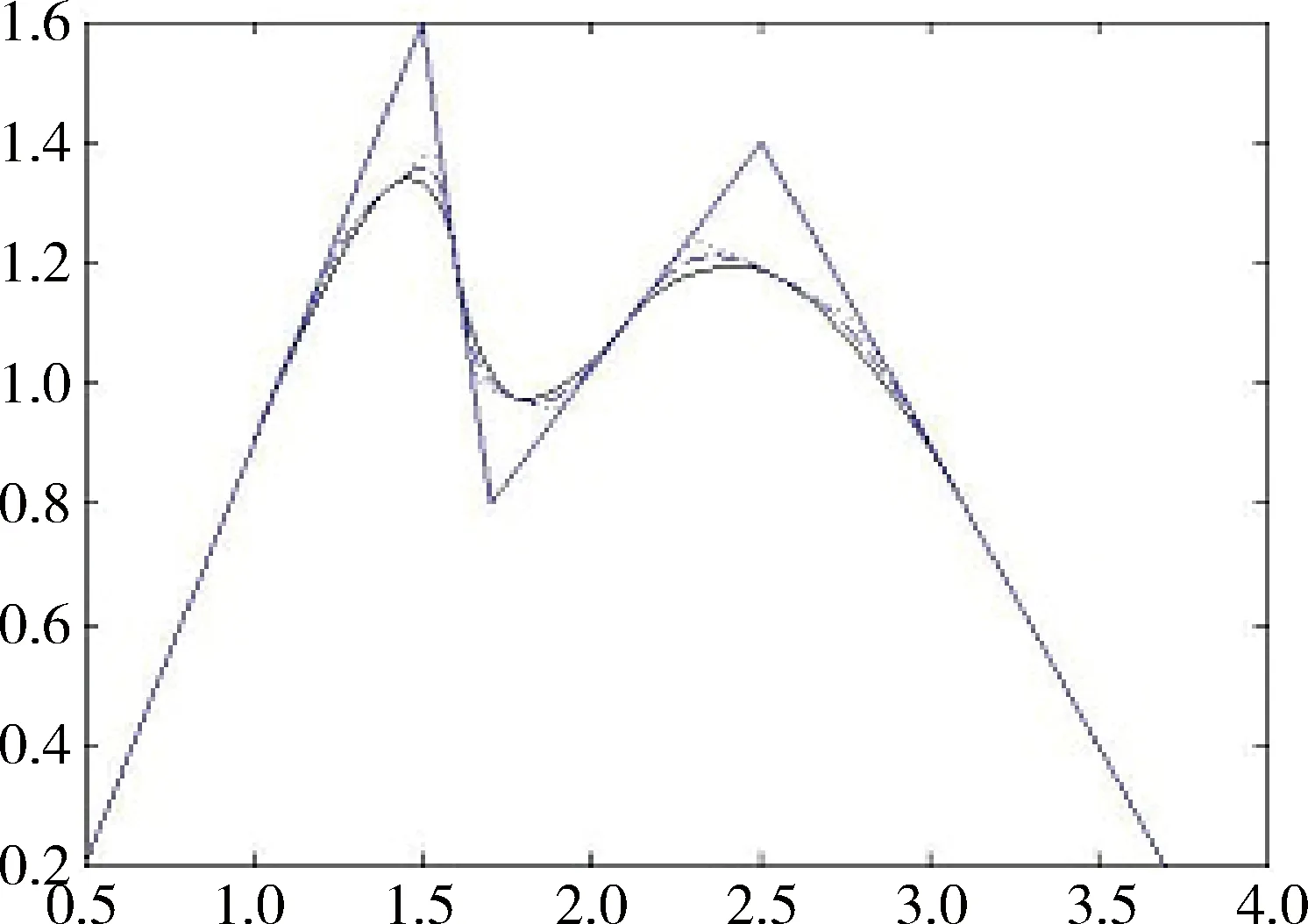
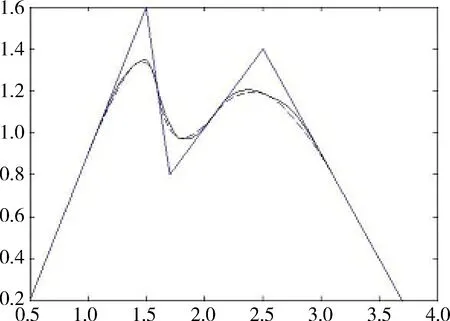
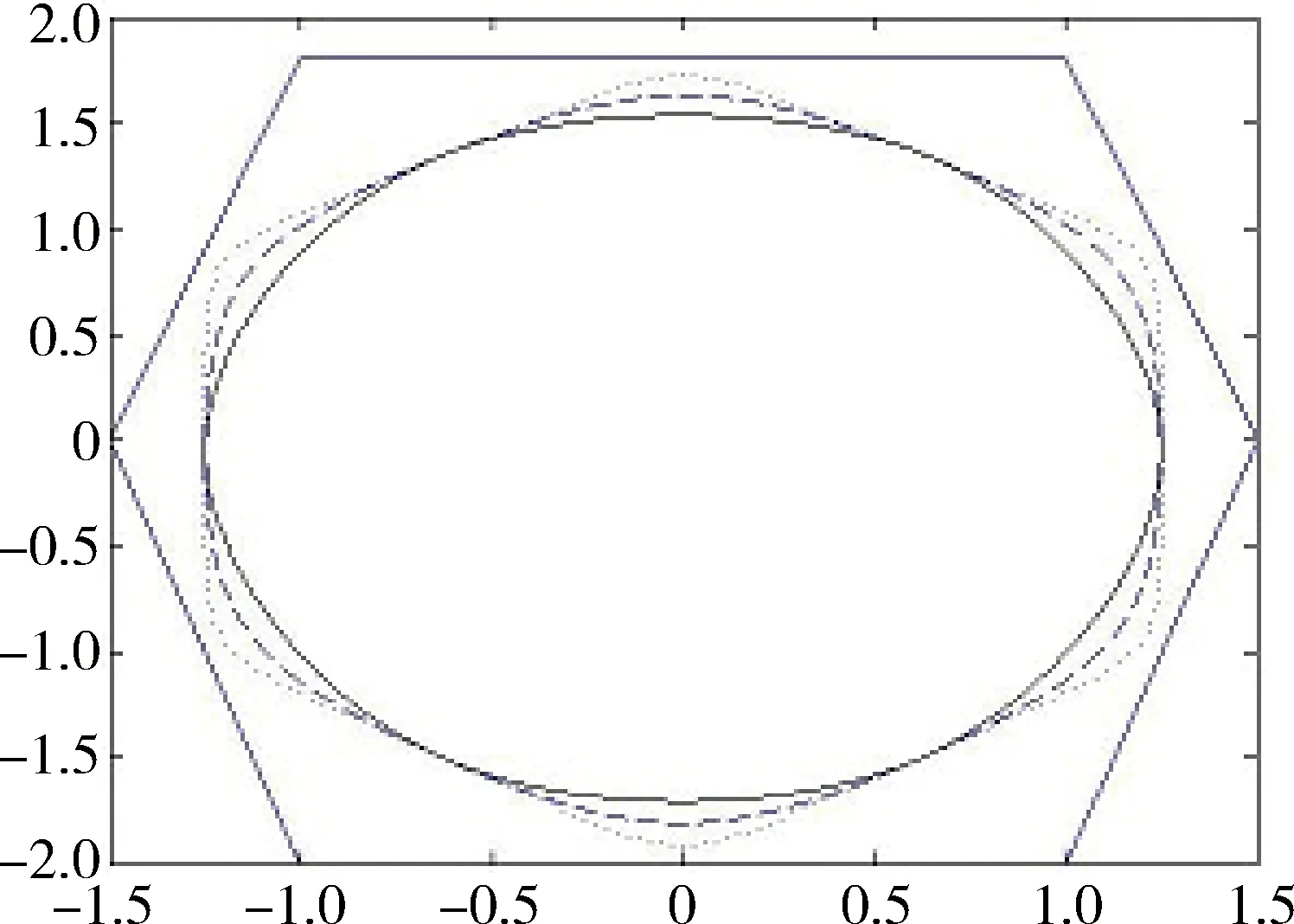
定义1 任给节点u0 bi(u)= (1) 为第i个带形状参数μi,λi+1,μi+2,λi+3的非均匀二阶三角B样条基函数。其中 从式(1)可知基函数具有如下性质: 性质1:当ui 性质2:当u0≤u≤ui或ui+4≤u≤un+4时,bi(u)=0; 性质4:在实际应用中有时需要利用重节点技术,与单形状参数情况类似,当基函数的节点重数k≤4时,这时只要把对应的区间缩小为0,并去掉基函数的相应段即可。例如当ui+3=ui+4时,Δui+3=0,进行如下定义: bi(u)= (2) 容易证明重节点时多形状参数的基函数的连续性有如下定理: 定理1 如果u=uj是基函数bi(u)的k(k=2,3,4;j=i+1,i+2,i+3,i+4)重节点,则基函数的支撑区间从4减少为5-k段,k=2,3时基函数连续,k=4时不连续。 图1表示重节点时的基函数,这里的节点u=0为三重节点,可知由于参数的取值不同,多形状参数的二次三角多项式基函数(虚线)呈现不对称,单形状参数的基函数(实线)对称。 图1 重节点时的基函数 定理2 设节点向量U={u0,u1,...un+4}满足u0 由αi,βi的定义可知: 经计算可得: 图2表示均匀节点下的基函数的图像。其中实线表示形状参数λi=μi=1时 ,即单形状参数的情形;虚线表示均匀节点下多形状参数的基函数图像,虚线对应的λi=(0.4,1,1,0.8,0.3,0),i=1,2,3,4,5 ;μi=(0.5,0.8,0.2,0.4,0,0.1),i=0,1,…4。 图3表示形状参数λi、μi对非均匀节点的基函数的影响。其中节点向量为U={0,2,5,6,8,12,13,15,20,27},实线表示单形状参数的基函数图像,虚线表示多形状参数的基函数图像,形状参数的取值与图2相同。由此可见,多参数对基函数的影响使其左右发生变化,故可作局部调控。 图2 均匀节点的基函数 图3 非均匀节点的基函数 定义2 任给R2或R3中的控制点p0,p1,...pn,节点向量U=(u0,u1,...,un+4)及形状参数-1<λi,μi≤1,则: (3) 称为多形状参数的二次非均匀三角B样条曲线,其中bi(u)由式(1)所定义。 当ui (4) 由基函数的定义可知,式(4)定义的曲线实际上含有4个形状参数μi、λi+1、μi-1、λi,利用这些参数可以达到整体及局部可调,以下分两种情况讨论: (1)当μi=λi=μi-1=λi+1=μ时,即为单参数曲线,αi、βi与形状参数无关,μ增大时,曲线越靠近线段Pi-2Pi-1,μ起整体调控的作用。图4的曲线从上到下μ=1、0.5、0。 (2)当λi≠μi-1且μi≠λi+1时,这时αi、βi与形状参数有关,当λi=-1,μi=-1 时曲线段为直线段Pi-3Pi。图5中,曲线2的μ1=-0.5,λ2=0.8,μ3=-1,λ4=0.2,可见曲线右端变而左端不变;曲线3的μ1=1,λ2=-1,μ3=1,λ4=0.5,曲线左端变而右端不变;曲线1参数取μ1=0.5,λ2=λ4=0.8,μ3=-1,可见多参数比单参数更具灵活可调控性。 图4 单形状参数曲线 图5 多形状参数曲线 定理3 如果给定4个控制顶点Pi-3(-a,-b),Pi-2(-a,b),Pi-1(a,b),Pi(a,-b),其中a、b是均不为0的实数,节点等距,且令λi=μi=0,当u∈[ui,ui+1]时,ri(u) 为一段椭圆弧。 证明: 根据式(4) 经计算,有 (5) 这即为椭圆的四分之一参数方程。 推论1 对于二次三角B样条曲线,如果控制顶点为P0(-a,-b),P1(-a,b),P2(a,-b),P3(a,-b),P4(-a,-b),P5(-a,b),P6(a,b),则ri(u) 为一段椭圆。若a=b,则为整圆。图6为椭圆。 图6 椭圆 开区间和闭曲线的构造是曲线设计中的基本内容,为保证生成开的二次三角B样条曲线,只要令p0=2p1-p2,pn+1=2pn-pn-1,可构造插值于p1和pn且在u1和un处分别以p2-p1和pn-pn-1为切向量的开三角B样条曲线。图7表示单形状参数,λi=μi=0,0.5;图8表示多形状参数,实线对应λi=(0.4,0,0,0,-0.5,0,0.8),i=2,3,...,8,μi=(0.5,0.8,0,2,0.4,0.5,-0.2,0),i=1,2,...,7。 图7 单参数下的开曲线 图8 多参数下的开曲线 图9 单形状参数下闭曲线 图10 多形状参数下闭曲线 本文给出了在非均匀节点情形下多参数的一类二阶三角B-样条曲线,该曲线是基于四点分段,即曲线每一段只与4个控制点有关。同时它也具有二次B样条曲线的许多重要性质,如连续性、凸包性、几何不变性等。并且通过参数的取值不同可以达到整体或局部形状调控,应用重节点的技巧可以生成以此类基函数构造的开曲线和闭曲线。此外,它还可以表示椭圆及圆等圆锥曲线。 [1] 李成刚,冯静,凌玲.基于WPF交互式绘图系统的开发[J].微型机与应用,2011,30(6):50-52. [2] SCHOENBERG I J. On trigonometric spline interpolation[J].J.Math.M.,1964,13(5):795-825. [3] Han Xuli. Piecewise quadratic trigonometric polynomial curves[J].Mathematics of Computation, 2003,72(243):1369-1377. [4] Han Xuli. Cubic trigonometric polynomial curves with a shape parameter[J].Computer Aided Geometric Design,2004,21(6):535-548. [5] 吴晓勤,韩旭里.带参数的二次三角多项式样条曲线[J].工程图学学报,2006,27(1):93-97. [6] 王文涛,汪国昭.带形状参数的三角多项式均匀B样条[J].计算机学报,2005,28(7):1192-1198. [7] 谢进,邬弘毅,邓四清,等.多形状参数的二次非均匀三角多项式曲线[J].工程图学报,2007,28(5):291-295. [8] 王晶昕,王迪.均匀结点情形下的两类二阶三角B样条曲线[J].辽宁师范大学学报:自然科学版,2014,37(3):297-303. Littelfuse双向瞬态抑制二极管阵列保护高速接口免受ESD侵害——适合保护HDMI、USB2.0、USB3.0和eSATA等高速接口 中国,北京,2017年3月28日讯——Littelfuse公司作为全球电路保护领域的领先企业,今日宣布推出了一个旨在保护电子设备免受破坏性静电放电(ESD)损坏的瞬态抑制二极管阵列(SPA®二极管)系列产品。 SP3042系列双向分立型瞬态抑制二极管阵列包括采用硅雪崩技术制造的反向瞬态抑制二极管,它可安全吸收IEC 61000-4-2国际标准(±30 kV接触放电)所规定最高值的反复性ESD震击,而不会造成性能减退。 当空间利用率极高的01005封装存在交流信号时,反向配置可为数据线提供对称ESD保护。 该系列产品的低负载电容(VR=0 V条件下为0.35 pF,典型值)使其成为保护HDMI2.0、USB2.0、USB3.0和eSATA等高速接口的理想选择。 SP3042系列瞬态抑制二极管具备下列关键优势: •双向设计可确保在印刷电路板(PCB)上放置零件时实现组装灵活性。 •可在整个工作电压范围内提供线性频率响应性能,这是高速接口保护的一个重要考虑因素。 •低动态电阻(仅为0.5 Ω)使其能对ESD事件作出快速响应。 •为电压高达30 kV和浪涌电流高达2 A(8/20 μs)的高速接口提供全面的ESD保护。 (Littelfuse公司 供稿) A type of trigonometric B-spline curves in non-uniform knot area Xie Yudi,Jiang Xinxin (School of Mathematics, Liaoning Normal University, Dalian 116029,China) The basis function of non-uniform trigonometric B-spline with shape parameter is constructed and its properties and variation of basis function at the multiple points are discussed.Based on the basis function,a trigonometric B-spline curve is defined.This curve possesses properties similar to those of quadratic non-uniform B-spline. By changing values of the shape parameters,it can adjust the curve shape without changing the control points.Besides, the circle and ellipse can be represented with the basis function accurately. non-uniform B-spline;basis function;curve design TP391 A 10.19358/j.issn.1674- 7720.2017.07.014 谢宇迪,蒋新昕.非均匀节点情形下的一类三角B样条曲线[J].微型机与应用,2017,36(7):46-49. 2016-12-14) 谢宇迪(1993-),通信作者,女,硕士研究生,主要研究方向:计算机辅助几何设计。E-mail:897233076@qq.com。 蒋新昕(1993-),女,硕士研究生,主要研究方向:计算机辅助几何设计。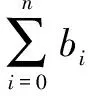
2 基函数的连续性
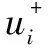
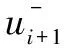
3 二次三角B样条曲线
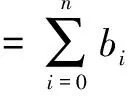
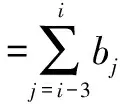
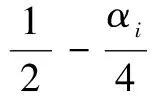


4 椭圆及整圆的表示

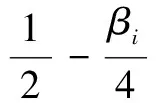

5 实例应用
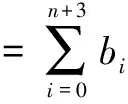

6 结论

